外尔半金属及其输运特性

张智强 ，蒋庆东，陈垂针 ，江 华∗

1苏州大学物理与光电能源学部，苏州，215006 2长沙理工大学物理与电子科学学院，长沙，410076 3斯德哥尔摩大学物理系，瑞典斯德哥尔摩，10691 4香港科技大学物理系，香港九龙，清水湾5苏州大学高等研究院，苏州，215006

目 录

I.引言101

II.外尔半金属 103

A.手性反常 104

B.外尔半金属在磁场中的朗道能级 106

C.外尔半金属的贝里曲率 107

III.无序对外尔半金属的影响 109

A.量子极限下外尔半金属的负磁阻 109

1.模型与方法 109

2.半经典玻尔兹曼输运理论 110

3.数值结果 111

4.讨论和结论 113

B.第一类外尔半金属中的无序与金属–绝缘体相变 113

1.背景与主要结果 113

2.自洽玻恩近似 115

C.第二类外尔半金属在无序条件下的相图 116

1.第二类外尔半金属背景简介 116

2.模型和干净样品的相图 117

3.转移矩阵的数值结果 118

4.自洽玻恩近似 120

IV.外尔半金属中拓扑Imbert-Fedorov效应 120

A.背景

120

B.weyl半金属体系中的IF位移 121

C.半经典运动方程 123

D.IF位移导致的反常速度 123

E.总结 124

V.外尔半金属中单杂质波包散射效应 125

A.背景 125

B.手性保护位移 126

C.半经典分析 126

D.波包散射 127

VI.总结 128

致 谢 128

参考文献 128

I.引言

因为量子霍尔效应[1]的发现，物理学家认识到一种不能用朗道的二级相变理论来解释的相变。这类相变中并没有发生对称性破缺，但是却有明显的物理特性的变化[2]。而后物理学家将拓扑的概念引入到物理学中，完美的解释了量子化的霍尔平台[3]，并在此基础上建立了一套完整的绝缘体拓扑态理论。霍尔丹提出了量子反常霍尔效应的设想使体系摆脱了对磁场的要求[4]。2005年，Kane与 Mele提出在石墨烯体系中引入内禀自旋轨道耦合（σ轨道与π轨道之间的混合[5]）可以产生量子自旋霍尔效应[6]，进而使得人们认识到了制造低功耗甚至无功耗自旋电子学器件是完全可行的。现在与拓扑态相关的领域已经成为物理学的一个重要研究方向[7−8]。

狄拉克在满足协变以及相对论的情况下给出了自旋为ħ/2的粒子所满足的方程，即我们熟知的狄拉克方程，外尔在此基础上得到了满足手征要求的外尔费米子所满足的外尔方程。这些方程描述的粒子原本是高能领域的概念，但在石墨烯等材料被成功制备并被大量研究后，凝聚态物理学家发现：既然我们可以用准粒子激发模拟狄拉克费米子[9−10]，那为什么不能用材料产生各类准粒子激发使得这些准粒子满足相应粒子的基本方程，这样我们就可以研究这些原本是高能领域的基本粒子。在高能中能标非常高，这使得产生基本粒子需要耗费巨大的能量，而材料中低能标下的有效理论与高能标下的行为竟然可以如此地一致，对它们的研究将大大节省实验资源与人力成本。我们所知的三类费米子包括狄拉克费米子、外尔费米子、马约拉纳费米子[11]，它们最近分别在真实材料中的准粒子中激发“产生”[9,12−13]。

为了实现外尔费米子，2011年南京大学的万贤纲等人率先在凝聚态体系中提出了外尔半金属的概念[14]。 随后在物理所翁红明等人 TaAs的理论预言[15]指导下，外尔半金属被实验证实[16−17]。在固体物理中我们根据带隙的有无将材料分为导体和绝缘体。但如果我们考虑一个体系存在能带在动量空间的线性交叉，该体系将区别于绝缘体和金属，这是因为在交叉点体系态密度接近于零，但体系又不存在带隙。因此如果存在满足外尔方程的准粒子激发，并且具有半金属特性[12]，该体系就被称为外尔半金属。

因此，理论上为了获得外尔半金属，只要让两个非简并的能带线性交叉即可。而同时存在时间反演对称和空间反演对称会提高能带在高对称方向的简并度，这预示着需要寻求一些特殊的结构使得体系的对称性降低，从而实现非简并交叉的能带，使得体系处于拓扑非平庸的状态（破缺空间反演对称的体系至少存在四个外尔点，每个点的手性均满足|C|=1,而破缺时间反演[18]，只能产生一对外尔点[19]）。除了第一类外尔半金属，极度破坏洛伦兹规范不变性的外尔半金属也被提出[20]，它们被称为第二类外尔半金属。这一体系在理论提出后很快被实验验证[21]。我们知道空间中不满足洛伦兹变换的粒子是不能稳定存在的，但是真实材料中准粒子激发并不需要满足洛伦兹不变性，这就使得凝聚态物理学家能够研究这一类高能领域所不存在的准粒子激发。

外尔半金属最重要的特点之一就是手征反常[22−23]，即当电场与磁场平行时，手性粒子并不守恒，一种手性外尔费米子会转化成另一种手性费米子，而这在输运中将表现出非常不同于拓扑绝缘体的特性：负磁阻效应[24−26,50]、线性磁阻[27]和手征磁效应。并且外尔半金属的另一个重要特点为表面态不连续，而且表现为两段费米弧[28]。费米弧上的每一个点都是拓扑非平庸的，外尔点受拓扑保护，这使得外尔半金属很稳定[29]，只有当两个外尔点混合成为一个狄拉克费米子后带隙才能被打开[30]。这种受拓扑保护的体系一般都比较稳定，而材料特性的稳定性一直是人们追求的，这也是拓扑态受到大量关注的原因。

输运特性是拓扑材料最重要的物性之一，它们对发展量子计算、低功耗器件、以及介观逻辑器件都有重要意义。在特定条件下，拓扑态材料会表现出完全不同的输运结果，如量子自旋霍尔效应会产生量子化的纵向电导平台。虽然这些平台不需要强磁场条件，但是因为对退相干很敏感[31]，量子化现象并不能像量子霍尔效应那样在大量破坏时间反演的杂质存在以及宏观样品中被观测到。在拓扑绝缘体领域，人们提出了拓扑安德森绝缘体的概念[32−33]，即原本体系处于拓扑平庸态，但是随着无序的引入，系统发生拓扑相变，从绝缘体相进入拓扑非平庸相。继续增大无序，所有的电子进入局域态，体系进入绝缘体相[34]。 通过以上分析，可以预期外尔半金属在不同无序条件下会出现不一样的新的输运性质，因为真实材料必然存在一定的无序效应，因此研究无序对外尔半金属的影响是很必要的。有关无序对拓扑态影响的更多介绍可参考文献 [35]。本篇综述中我们将介绍外尔半金属在无序下的输运[36]以及无序存在时第一类外尔[37−38]半金属以及第二类外尔半金属的相图[39]，并且分析了无序诱导的各类相变。我们也将回顾外尔半金属中的Imbert-Fedorov位移，及其潜在应用[40−41]。最后我们介绍通过引入散射时的手性保护位移抑制大角散射这一机制，解释外尔半金属中，超高载流子迁移率的物理起源[146]。

本综述分为五部分，第一部分我们介绍和外尔半金属基本概念和输运相关的背景知识。第二部分我们介绍无序对外尔半金属的影响，包括量子极限下的输运特性，第一类和第二类外尔半金属的相图。第三部分，我们展示外尔半金属中的IF位移及其潜在应用。第四部分，我们通过引入手性保护位移给出了外尔半金属中超高载流子迁移率问题的一种可能解释。最后我们给出一个简单的总结。需要指出的是本综述侧重于我们过去完成工作领域的研究进展，关于这一领域的优秀综述有很多，有关外尔半金属领域的更多背景可参考综述文献[25−27,42−50]。

II.外尔半金属

薛定谔方程不满足相对论要求（不满足协变要求）。协变性原理要求时间和空间是平权，因此物理学家在薛定谔方程的基础上，提出了满足协变要求的克莱因–戈登方程（K-G方程）：

尽管满足相对论要求，K-G方程还是存在一定的缺陷。首先 K-G产生的量子态做内积时与时间有关，从而导致概率不守恒，其次K-G方程是时间的二阶方程，求解需要时间一阶导数的量化关系才能得到完整的结果。

狄拉克分析K-G方程的问题所在是因为时间的二阶导，如果建立一个时间一阶导数，并且满足协变要求，这些问题就迎刃而解了，这就是描述ħ/2自旋的费米子满足的方程

其中γµ是γ矩阵。因为需要定义四个矩阵，很显然2×2的三个泡利矩阵并不够。而通过群论的计算，我们选择满足要求并且维度最低，即4×4的情况。从有限群的方面分析，用γµ(µ=0,1,2,3)，作为生成元，群元是有限的，共有32个，这三十二个群元构成一个狄拉克群。通过分类我们发现共有17类。按照群中元素的总和等于群表示所有元素的数量，我们得到两种情况：12个一维表示加5个二维表示，或16个一维表示加1个四维表示。考虑到需要满足γ矩阵的对易关系，四维群表示才是满足要求的，这是因为二维只能给出三个σ矩阵满足对易关系，而一维群表示并不满足对易关系。

为了更好的描述极端相对论粒子，我们把狄拉克方程写成块对角形式:

这里采用外尔表象，m代表质量，因为五个γ矩阵的定义有一定的任意性，我们经常采用的有狄拉克表象，外尔表象与马约拉纳表象[51]，这三种表象下分别可以更简便地描述狄拉克费米子，外尔费米子与马约拉纳费米子。这些表象都是彼此等价的，并且可以通过群论的手段加以证明。

当质量m=0的时候，方程变为

这就是外尔方程，即外尔费米子满足的方程。通过这个方程可以进一步按照量子场论中投影算符[52]的定义或采用自旋在动量的投影C=p·σ/p来定义手性。我们容易发现外尔方程和投影算符对易，因此外尔费米子具有特定的手性。值得注意的是左右手性的定义是相对的，如果说满足Eq.(4)中下式的外尔费米子称为左手外尔费米子，那么满足Eq.(4)中上式的外尔费米子是右手外尔费米子。下面我们将讨论m=0的情况下狄拉克费米子与外尔费米子的所满足方程的区别，它们分别满足：

从上两式我们不难发现，Eq.(5)中不同手性的费米子出现在动量空间的同一点，而外尔半金属的两个外尔点在动量空间是分开的，这就是为什么狄拉克费米子不具有手性，而外尔费米子具有手性。因此定义低能激发满足HW的材料为外尔半金属。通过在动量空间计算外尔半金属和狄拉克半金属的贝里曲率(Berry Curvature)，外尔半金属的每一点都具有非零的贝里曲率(正负对应不同手性)，而狄拉克半金属每一点的贝利曲率都是零。贝里曲率矢量可以看作动量空间中的磁场，由于Ωk有磁单极形式，外尔点可以看作动量空间中的磁单极子。而且对于外尔半金属，两个磁单极是手性相反并且空间分离的。另外通过贝里曲率和对称性分析我们可以知道，为什么外尔半金属需要破缺时间反演或空间反演对称。因为只有在这个情况下，贝利曲率才不为0。贝里曲率在空间反演下的满足 Ω(k)=Ω(−k),时间反演下满足 Ω(k)=−Ω(−k)，当两个对称性同时存在时，很显然存在Ω(k)=−Ω(k)，贝里曲率必然为零。因此只有破缺掉一种对称性或两种对称性全部破缺，这样才有可能获得非零的贝里曲率，从而才可能获得外尔半金属。

图1.(a)(b)破缺空间或时间反演对称性狄拉克锥发生简并劈裂，产生两个外尔点，两个外尔点通过费米弧连接。(c)对于kx=k1表示两个外尔点外的切片，无边缘态，拓扑平庸。(e)表示kx=k0的切片，因为两个外尔点之间的切片存在非0陈数，所以k0拓扑非平庸，具有边缘态。图片来自文献[28]。

虽然外尔半金属在磁性材料中（破坏时间反演对称的体系）中被预测[14]，但是由于表征困难，这些材料到目前为止仍并没有完全被实验证实。因此人们将目标转向了破缺空间反演对称的材料。2015年翁红明等人提出的TaAs[15,44]很快被中科院以及普林斯顿大学的课题组通过角分辨光电子能谱观察到了线性色散和费米弧结构[16−17]，从而验证了TaAs就是外尔半金属。

图1展示了外尔半金属的基本能带特征，一个狄拉克点通过对称破缺产生两个具有手征的外尔点。外尔点附近体能带具有线性色散结构，而表面对应连接两外尔点的费米弧表面态（一段不连续的费米面）。图(c)～(e)通过切片演示了外尔半金属拓扑能带的物理起源，两个不同手性外尔点之间的任意切片kx=k1存在非0的陈数，因此有无能隙的边缘态激发，具有拓扑非平庸的能带结构。而外尔点外的切片kx=k0陈数为0，不存在无带隙边缘态激发，因此能带结构是拓扑平庸的。这些拓扑非平庸的边缘态在动量空间连续分布构成体系受拓扑保护的表面态。外尔半金属独特的能带结构将导致许多新奇的物性及输运性质，以下我们做简单介绍。

A.手性反常

我们将简单介绍一下外尔半金属的手征反常以及由此导致的一些输运中的反常特性[24]。材料中的手性反常最先由 Nielsen和 Ninomiya提出[53]。具体表现为：当电场和磁场平行于电场诱导的电流时，体系的手征费米子不再守恒。相应的，定量关系如下：

其中Nc=(N+−N−)/2为手性荷的数目。体系虽然手征荷不守恒，但是总粒子数仍然守恒。我们遵照文献[62]的思路通过场论的方法简单推导手性反常这一项的产生及其隐含的物理效应。需要指出的是，手征反常不仅可以采用场论的方法[56]，玻尔兹曼方程[54]也可以帮助我们获得手性反常。场论下给出作用量[55]：

其中为ϕ的狄拉克共轭，第一项表示引入电磁场后的广义动量，第二项为质量，第三项为轴矢量。若bµ=(b0,b),则b给出两个手性相反的外尔点在动量空间的矢量差值，而b0给定两个外尔点的能量上的差值[55]。 通过此拉氏密度我们可以得到与Eq.(8)相对应的哈密顿量密度，这不仅可以验证轴矢量的物理意义，也能够证实这个作用量就是描述外尔半金属的作用量。其中γµ是通常定义的四维γ矩阵，而γ5=iγ0γ1γ2γ3。 对应外尔费米子，我们令m=0，作路径积分，得到配分函数形式：

为了检验手性流(chiral current)在手性变换下是否守恒，首先对作用量做手性变换，场算符在手征变换[58]下的结果：

注意到 [γ5,γµ]+=0,其中θ(x)很小，可以认为这个对称操作对应李群,右下角的正号表示场算符满足费米子的对易关系，最后定义协变微分Dµ=∂u+iAµ。 令∂µ作用在右侧的 e−iθ(x)γ5ϕ会产生两项，将θ写成如下形式偏微分作用后的结果为左侧的狄拉克共轭被手征变换的结果替代后需要和γµ做一次位置交换，这会将γ5变为−γ5。当θ(x)=2bµxµ=2(b·r−b0t)，作用量的轴矢量被消除，从而获得一个无质量狄拉克场的作用量

不难证明，我们将轴矢量消除的过程中，手性流以及总流都是守恒的[22]。手性变换只是移动两个外尔点的的动量位置和能量，并且可以将两个手性相反的外尔费点合并成一个狄拉克点。为了最终展示量子条件下手性变换的结果，我们还需要检验测度在手性变换下如何改变，容易得到：

行列式部分表示手性变换导致的测度变化，称为 Jacobian[56]，并且有 ∆Sθ=Tr[θ(x)γ5]. 其中求迹并不是单纯对γ5直接求迹，而是对所有量子态的平均的积分或求和[22]，变换后的整个配分函数为

我们希望检验电磁场Aµ和手性变换θ(x)是否存在耦合，若存在耦合它们的耦合形式如何？我们选取ϕn为作用量γµDν的本征态，满足方程γµDνϕn=ϵnϕn和采用 Fujikawa热核规范化[56]从而解决的求和问题。为了使得求和不至于发散，需要在求和公式内引入衰减因子，并且已知电磁场张量Fµν=∂µxν−∂νxµ，详细过程可见文献[56]。最终解得：

从而可以得到手型变换下的配分函数，根据诺特定理[52]：

此时手性流已经不再守恒，从而得到手性反常项：

代入电磁场张量，并做简单计算，获得三维形式：

这一形式表示，当电场与磁场不正交时，手征流不守恒，这会造成一种手性外尔费米子转化为另一种手性费米子的过程在真实材料中发生。下面我们将看到手性反常是产生负磁阻以及手征磁效应的原因。将Fµν=∂µxν−∂νxµ代入A(x)的表达式，得：

获得反常项的作用量：

分部积分，全微分的表面项丢掉，获得以下形式:

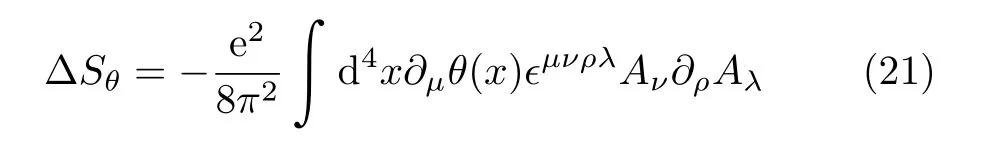
类比Chern-Simons形式，可以发现这一项似乎与量子霍尔效应有关。按照Chern-Simons规范场推导霍尔效应的方法，我们计算流

展开后的结果为：

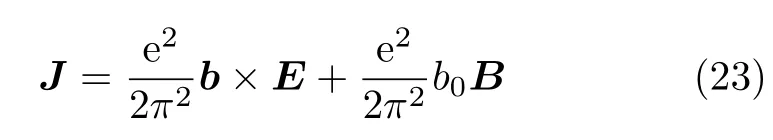
其中b表示两个手征不同的外尔点的动量差，当b与E不平行时，等式右侧第一项可以在动量空间形成类似洛伦兹力的作用力，因此该项对应反常霍尔效应。而等式右侧第二项对应手性磁效应，由于b0表示两个外尔点的化学势的差值，所以当b0不等于0时，理论上来说外磁场可以诱导出一个平行于磁场的电流。但是在凝聚态体系中手性磁效应是否能够存在？我们知道磁场是不能做功的，如果这样的手性磁效应被允许存在的话，这将是一个非常惊人的结果。经过数值计算的确认，我们发现两个外尔点之间虽然处于不同的能量位置，但因为整个体系具有一个明确的化学势，手性磁效应并不能诱导出净电流[54]，随后的工作也确认了我们的结论[61]。我们倾向于相信，当两个外尔点的化学势不同，磁场可以诱导出一个净电流，而当两个外尔点达到化学平衡时，手性磁效应的效果不能在输运中体现效果。关于手性反常的更多计算细节可参考[62]。

需要强调的是，手性反常是一种纯量子效应，它并没有经典对应。从这一小节的证明不难看出，与经典对应的作用量在手性变换下并不会造成手性流的不守恒，但是与量子场论对应的配分函数中的测度项在手性变换下会造成手性流的不守恒，这也就对应手性反常。因为是量子化引起的反常效应因此在场论中也被称为量子反常。

另外需要指出的是，验证外尔半金属的较为准确方法就是采用角分辨光电子能谱观测费米弧结构。然而角分辨光电子能谱方法并不简便，因此实验上需要一些更易于操作的实验方法来准确验证外尔半金属相。手性反常导致的负磁阻被认为是外尔半金属在输运方面的重要证据，被多个实验组观测到[69−74]。 如图 2所示，实验上观测到外尔半金属的负磁阻效应[50]，随着磁场与电场的夹角的减小，纵向电阻率从最初随磁场的增大而增大，到最终电阻率随着磁场的增大而减小。从物理图像上来看，手性反常使得一种手性费米子增多，另外一种手性费米子减少，形成朗道能级之后，两种外尔费米子的传播方向是相反的，这会造成沿着电流的准粒子增多从而使得电阻减小，磁场越强手性反常越强，参与输运的准粒子越多，使得电阻减小得越剧烈，在下一小节我们会展示这一结果。需要强调的是，虽然负磁阻是外尔半金属的一个特性，但是并不是只有外尔半金属才存在负磁阻效应[75]。

图2.外尔半金属中的负磁阻效应，磁场与电场在电流方向的投影不为0的情况下，在纵向观测到电阻率随着磁场的增大而减小的效应。图片来自文献[50]。

B.外尔半金属在磁场中的朗道能级

上一小节，我们采用场论的方法推导了手性反常，但是在热核规范化方法中，我们将费米子场与规范场同时存在的协变导数的本征态取为平面波，因此这一方法在强磁场下并不适用，而且给出的物理图像也并不十分清晰。但是在实际情况中，磁场会令体系建立朗道能级，磁场越大朗道能级间隔越大。而且对于外尔半金属，强磁场下会存在独特的手征朗道能级，而手征朗道能级能够展现出更加直观和清晰的手性反常机制的物理图像，以下我们简单推导这一结果。

假设磁场与电场都沿着z方向，即B=(0,0,B)，B＞0，选取洛伦兹规范A=(−By/2,Bx/2,0)，其中A为矢势，满足B=∇×A。矢势的引入使得真实动量变成了广义动量，即P→P−A，这里为了书写简便，令|e|=1,νF=1。 我们首先分析手性为C=−1的部分。其中C=1的外尔点满足的哈密顿量H=−k·σ，而C=−1的weyl费米子满足的哈密顿量为H=k·σ。写成矩阵形式为:

根据对易 [x,kx]=i,[y,ky]=i，Ax=−By/2,Ay=Bx/2,得到

定义a†a|n〉=n|n〉。我们得到粒子数算符下的新哈密顿量：

朗道能级通过解本征方程HΦn=EnΦn得到。我们可以看出只有下面的形式解满足要求有意思的是，当n=0时，有Φn=(|0〉,0)†。代入Eq.(27)，我们得到第0级朗道能级满足的色散关系只能为E0=νFkz。同理改变条件并重复以上计算，我们可以得到C=−1的外尔点以及B＜0下的结果。最终我们得到一个概括各种情况下最低朗道能级能量的公式：

其中sgn(x),表示当x＞0,sgn(x)=1;x＜0,sgn(x)=−1。当C＞0,B＞0,E=−νFkz;C＞0,B＜0,E=νFkz;C＜0,B＞0,E=νFkz;C＜0,B＜0,E=−νFkz全部四种情况均给出。从上式看出，在确定磁场下，两种手性费米子的运动方向完全相反。

图3演示了强磁场下的手性反常。上图表示当引入磁场以后体系形成朗道能级，可以看到两个手性的第0朗道能级，没有电场的情况下，这两种手性粒子的动量是相同的，因此没有手性反常。但是当我们引入电场以后,电场加速粒子 ħ∂k/∂t=eE,说明粒子的动量将会随着时间而变化。而这个变化将造成一种手性的费米子增多，而另外一种手性的费米子减少（图3下图所示），这就是手性反常，详情可参考[23]。虽然两种手性费米子的粒子数不守恒，但是总的粒子数是守恒的。我们不难发现，电场的作用支持电子沿着电场的反方向运动。当磁场和电场方向平行时，这等价于利于某种手性费米子，而不利于另外一种手性的费米子。

图3.(a)(b)对应无电场，磁场存在下，体系建立朗道能级并且存在具有手性的第0级朗道能级，分别对应左右手性费米子，当无电场时可以看到两种费米子的化学势相同。(c)(d)表示引入电场，并且电场平行于磁场的情况下，一种手性的费米子减少了，另外一种手性费米子增多了。其中红色能带为全满的价带，而黑色能带为全空的导带，已填充的手性朗道能级对应黑色实心点。

因此手性为−1的费米子转化为手性为1的费米子，从而会造成两个外尔点的化学势差值∆µ=eE0ντ，τ为输运弛豫时间，进而诱导出一个电流：

该结果与Eq.(7)一致。它会导致纵向电阻的减小，而且磁场越大，手性反常越强，磁阻越小。

C.外尔半金属的贝里曲率

上文中，我们提到外尔半金属具有非零的贝里曲率，在本小节我们对它作简单介绍。 从微分几何的角度，一个矢量沿着流形的一个闭合回路平移最后回到起点时，如果初末矢量能够重合说明空间是平直的（曲率为零），而当两个矢量不再重合，就用非零的曲率来表征空间弯曲的程度[76]。 在拓扑态研究中，最重要的曲率是贝里曲率，它表示波函数在动量空间的弯曲程度并且与贝里相位紧密相关。贝里相位(Berry Phase)是贝里最早总结的[77]。把一个量子体系绝热演化回到初始状态时，会产生一个额外的几何相位：

定义在在非闭合回路中的γn并不满足规范不变性(Gauge invariant)，即规范变换以后我们可以额外增加一项从而使得这个相位被抵消掉。贝里考虑当把γn定义在闭合回路下时，规范变换只能给γn增加2π的整数倍，这并不能消除γn对体系的影响。因此闭合回路上定义的γn是规范不变的,被称为贝里相位。其中：

称为贝里矢势。从规范场的角度，An(R)是定义在主丛上的联络，而联络的协变微分就是曲率[78]。因此

分别是贝里曲率矢量(Berry curvature vector)以及贝里曲率张量(Berry curvature tensor)，它们存在关系：

ϵµνρ是全反对称张量（Levi-Civita全反张量）。而贝里曲率矢量可以看成在参数R空间（通常为动量空间）的磁场。定义的两个贝里曲率都是规范不变的，并且定义时不需要构造闭合回路。

前面我们给出了各向同性外尔半金属的贝里曲率矢量为这里从各向异性外尔半金属的哈密顿量出发，展示它的推导过程。体系哈密顿量表示为：

其中σx,σy,σz为泡利矩阵，νx,νy,νz为三个方向的费米速度，当νx=νy=νz就是各向同性的情况，这里采用了自然单位制ħ=1。从这个哈密顿量出发，我们可以获得体系的本征值与本征态，表示如下：

其中上下两式表示两个非简并本征态以及对应的本征波函数，它们分别对应导带和价带。

根据贝里曲率的定义Eq.(33),并作简单推导，我们可以得到

以下我们以计算曲率为例

考虑到∂H/∂kx=νxσx，因此有

〈+|和|−〉分别对应 Eq.(36) 和 (37)，〈+|=|+〉†，得到最终结果

重复上面过程，得：

将Eq.(43)代入Eq.(38),

最后根据量纲补齐了 ħ，我们获得了贝里曲率张量它表示导带在z方向的贝里曲率。此外，我们还得到了另外两个方向以及价带的贝里曲率：

写成矢量形式，此即为各向异性外尔半金属的贝里曲率。当νx=νy=νz=ν时，有

将上式代入曲率张量的矢量形式，得到各向同性外尔半金属的贝里曲率：

对Eq.(47)在第一布里渊区中做环路闭合面积分，得到

从上式可以看出外尔半金属的外尔点是一个拓扑的荷，与实空间的磁单极极其相似。

以上我们简单介绍了外尔半金属的基本概念以及与之具有密切关系的几种物性，包括所满足的方程、手性反常、负磁阻效应、磁场中的朗道能级和贝里曲率。下面将介绍过去几年我们在外尔半金属输运方面开展的一些工作。

III.无序对外尔半金属的影响

A.量子极限下外尔半金属的负磁阻

在文献[36]中，我们研究了处于强磁场中的外尔半金属在无序条件下的输运性质。因为长程无序和短程无序对外尔点间的散射以及朗道能级展宽行为的不同，因此我们分别研究了这两种无序的影响。在弱的短程无序下，对于第0级朗道能级，系统存在负磁电导率(negative magnetic conductivity)这与半经典的玻尔兹曼(Bolzmann)输运理论一致。而对于长程无序，当选取合适的关联长度并且不考虑屏蔽效应时(screening effect)，我们发现体系存在正的磁电导率。这是因为长程无序可以压制外尔点之间的散射并产生朗道能级的展宽。即使在弱无序下，高朗道能级辅助的输运(high Landau levels assisted transport)会占主导地位，这时候基于手性第零朗道能级的玻尔兹曼输运理论不再适用。我们的理论结果表明产生这类负磁阻的物理机制主要有两个：（1）当存在长程关联无序并且磁场很强的时候，高度简并的手性第零朗道能级之间的散射被压制；（2）当磁场增大的时候,高朗道能级辅助下的背散射被削弱。

1.模型与方法

我们考虑了外尔半金属的二带模型，哈密顿量为[19,79]：

其中这里ν,tz,mz,m0都是系统参数，而σx,y,z是泡利矩阵，体带能谱为：

令Ek=0得到两个外尔点在动量空间的坐标，这里研究的是沿着z方向的两个外尔点。在z方向加入磁场后，哈密顿量变为：

这里选取了规范势A=(−By,0,0)。解得第零朗道能级为：

而第±n朗道能级为：

其中以及磁长

将哈密顿量H0离散到立方晶格[80]。我们先采用以下近似随后作傅里叶变换即可得到实空间格点哈密顿量。离散化后的结果如下[81−82]：

其中这里x(y,z) 表示沿着x(y,z)方向的单位矢量。表示在第 n个格点位置产生 (↑,↓)的电子。简单起见，令a=1。 我们在离散化的体系中引入了各向异性的长程无序V(r)[83−85]。体系的哈密顿量写成：

对i的求和包含所有随机分布于 [r1,r2,···rn]格点的杂质，其中ri=(r||,rz)为空间坐标。Vi为安德森无序模型中的随机在位势能，在 [−W/2,W/2]之间均匀取值，其中W是无序强度。x-y平面与z方向的杂质势的作用范围 (impurity potential rang)分别是ξ||和ξz。 当ξ||=ξz，V(r)描述各向同性长程无序，而当ξ||=ξz→0，V(r)描述短程无序。长程无序表示我们在(ri,||,ri,z)引入的一个强度为Vi的无序，这个无序会在ri||,riz格点产生随着同(ri,||,ri,z)距离增大而衰减的势场。当杂质势的范围趋近于0时，就相当于某个格点处的杂质只作用在这一格点，这就是典型的安德森无序模型描述的情况。

首先我们考虑沿着z方向的两端口输运，在x−y取周期性边界条件。我们只把无序加在大小为Lx×Ly×Lz的中心区，两端半无限长导线则都不引入无序。为了计算中心区的本征电导率，需要将导线的接触电阻去掉，因此中心区的本征电导[86−88]为其中N为导线中对应的模式数，GLB是Landauer-B¨uttiker电导。满足GLB=e2/hTr[ΓLGrΓRGa][89]， 其中Gr(EF)=[Ga(EF)]†=[EF−Hcen−∑n=L,RΣn]−1是推迟/超前格林函数。线宽函数其中表示左右半无限长导线的推迟/超前自能，可以通过迭代或者转移矩阵求解[90−91]。 中心区的电导率被定义为σ=同时我们计算了在不同的无序强度W以及磁场ϕ下的态密度这里采用了核多项式方法[92](kernel polynomial method)，其中En是N×N无序哈密顿量矩阵的第n个本征值。数值参数设置为tz=m0=ν=1,mz=0,a=1,EF=−0.2,ϕ=Ba2/ϕ0。

2.半经典玻尔兹曼输运理论

当z方向存在强磁场时，系统沿着该方向有高度简并的朗道能级。如图4所示，不存在磁场时，可观测到外尔点位于动量空间存在磁场时，外尔点消失并形成独特的手性第零朗道能级。 我们采用玻尔兹曼方程研究体系的磁阻，在弛豫时间近似下[93]，电导率为：

其中τ(kF)是输运弛豫时间，表示粒子发生背散射所经历的时间，是z方向的费米速度。是干净样品的态密度。我们注意到费米速度νF随着磁场强度的增加而减小，而态密度N0(EF)随着磁场的增大而增大。弛豫时间按照玻尔兹曼方程的定义：

图4.不同磁场强度下的外尔半金属的色散关系。(a)磁场相位 ϕ=0； (b)磁场相位 ϕ=π/30。图片来自文献 [36]。

其中说明只有背散射能够在第零朗道能级间发生，它们对输运起决定性作用。其中最外层表示对所有无序取系综平均。我们将无序分成四小类，分别研究它们的弛豫时间以及电导率：

[1]短程无序。如果

由于νF随着磁场强度B的增大而减小，因此dσ/dB为负[94−95]。

[2]第一类长程无序。当长程无序满足

弛豫时间和电导满足：

其中ξ||和ξz分别是x−y平面和z方向的关联长度，ni是杂质浓度，

[3]第二类长程无序。对于各向异性无序

其中

[4]第三类长程无序。各向异性无序满足

其中同时成立的时候，三类长程无序均变成短程无序。而当ξz→0和ξ||→0有且仅有一个成立的时候，第一类长程无序分别转化为第二类和第三类长程无序。

当x−y平面内的无序很平滑的时候，即ξ||≫lB，我们发现电导率σ取决于态密度而且随着磁场增大而增大 (见 Eq.(67))。因为第零朗道能级的简并模式几乎独立，弛豫时间近似与 B无关 （见 Eq.(66)）。对于z方向的光滑无序ξz≫1/kF,因为费米速度随着磁场的增大而减小，Eq.(69)表明电导会随着磁场强度的增加而减小。但是由于背散射被压制（此时背散射需要大动量转移），导致弛豫时间非常长(见Eq.(68))，电导率还是非常的巨大。因此在这种情况下，高朗道能级辅助的背散变得很重要，导致 Eq.(69)的结果不再准确。此外，对第一类长程无序，尽管 Eq.(65)给出磁导率是正的，但是我们发现定量上并不准确。有意思的是当朗道能级间隔特别大时，因为体系的输运弛豫时间非常之大，此时体系就像一个弹道导体，玻尔兹曼输运理论，即Eq.(69)的结果，再次适用。

3.数值结果

图5(a)和 (b)分别是长程无序ξ||=ξz=2,ni=0.02与短程无序ξ||=ξz=0.01,ni=1条件下本征电导G在不同无序强度下的结果。我们发现对于特定的无序强度，不同尺寸的中心区的电导率σ会重合成一条曲线（如图 5(c)和(d)）。 图 5(c)显示在长程无序情况下，电导率σ随着ϕ先增加后减小。通过分析玻尔兹曼输运理论的结果，在长程无序情况下，产生电导率峰的原因是态密度的增加和费米速度减小之间的竞争。而在图5(d)中，电导率随着磁场的增大而减小，这是由费米速度减小造成的。

图5.中心区本征电导 G在 (a)长程无序ξ||=ξz=2,ni=0.02和(b)短程无序ξ||=ξz=0.01,ni=1条件下随磁场ϕ的变化关系。(c),(d)分别与(a),(b)对应，但纵轴相应得替换为电阻率σ=GLz/(LxLy)。对于给定的无序强度W，我们选取了几种不同的中心区尺寸Lx×Ly×Lz，其它参数已在图中标出。图片来自文献[36]。

图6.物理量 σW2在(a)第一类长程无序ξ||=ξz=2,ni=0.02和(b)短程无序ξ||=ξz=0.01,ni=1条件下随磁场ϕ的变化关系。中心区尺寸Lx×Ly×Lz=20×60×100。(c)(d)分别与(a)和(b)对应，而纵坐标替换为态密度N(EF)，其中无序强度W 已在图中标出。图片来自文献[36]。

为了检验玻尔兹曼方程的正确性，我们计算了σW2,它应该正比于（这个结果可以通过 Eq.(63),(65),(67),(69)验证）。这个结果说明σW2应与无序强度W无关。也就是说，对于不同强度的无序，所有的曲线都应该是重合的。在图6(b)中（短程无序），这些曲线非常接近，表明玻尔兹曼输运的结果近似正确。在图6(a)中，峰值对应的磁场强度随着无序的增大而增大。因此对于第一类长程无序的情况，玻尔兹曼方程的结果并不符合实际的情况。此外我们发现在这种情况下的态密度已经严重偏离干净样品的结果（图6(c)）。而对于短程无序，这个近似是合理的。我们发现长程无序情况下，有较大的能级展宽，表明高朗道能级辅助的背散很重要。这种无序引起的大的能级展宽行为和以前强磁场下的无序二维电子气体系的态密度研究相一致[96−97]。 因此我们发现了一种不能用玻尔兹曼输运理论描述的正磁导率情况。下面我们将研究出现这一现象的物理机制。

图7.物理量 σW2在 (a)第三类长程无序 ξ||=0.01,ξz=2,ni=0.28和 (b)第二类长程无序 ξ||=2,ξz=0.01,ni=0.08条件下随磁场 ϕ的变化关系。中心区尺寸Lx×Ly×Lz=20×50×100。(c)(e)与 (d)(f)的参数分别与 (a)(b)对应，无序强度W 已在图中标出。图片来自文献[36]。

图8.物理量 σW2在 (a)第三类长程无序 ξ||=0.01,ξz=2,ni=0.28和 (b)第二类长程无序 ξ||=2,ξz=0.01,ni=0.08条件下随磁场 ϕ的变化关系。中心区尺寸Lx×Ly×Lz=20×50×100。(c)(e)与 (d)(f)的参数分别与 (a)(b)对应，无序强度W 已在图中标出。图片来自文献[36]。

前面我们已经指出分别当ξz→0,ξ||→0，第一类长程无序(ξz=ξ||)可以转化为第二类和第三类长程无序。为了更深入的理解各向同性无序效应对磁电导的影响，研究第二类以及第三类长程无序是很有必要得。

我们研究了弱的各向异性长程无序，如图 7(b)，我们发现在弱长程无序条件下ξ||=2,ξz=0.01,ni=0.08，σ出现一个电导峰。从Eq.(67)，可分析得出这是态密度与费米速度相互竞争导致的，并且σW2的曲线（图 7(e)）近乎重合，这表明这种情况下的输运结果可以采用玻尔兹曼输运方程来描述。但对于图 7(a)，ξ||=0.01,ξz=2,ni=0.28，我们观测到一个电导率峰。这是因为z方向的长程关联无序导致z方向大的输运弛豫时间，因此压制了kz方向的背散射。另外我们发现这种情况下σW2曲线并没有重合（图 7(c)），它意味着玻尔兹曼输运方程不适用。在图7(c)中，不难发现σW2随着W增加而下降。这是因为对于第三类长程无序，第零朗道能级内的背散射被压制，体系在z方向有非常长的输运弛豫时间。也就是说，这样直接的背散射不能发生，而这种高朗道能级作为中间态的散射变得十分重要。因此，z方向的长程无序情况下（第三类长程无序），高朗道能级辅助的背散射将会决定体系的输运性质。

如果继续增大无序强度，态密度将远远偏离干净样品，意味着费米面位置的能级展宽变得明显（图 8(e),(f)）。同时我们发现由于无序强度的影响，磁导率峰也会移动到一个更大的磁场强度位置（图 8(a)～(d)）。在长程关联强无序条件下，不仅费米面附近的能级展宽很重要，而且高朗道能级辅助的背散起决定性作用。随着磁场的增大，朗道能级间隔增大，导致弛豫时间增加，并且从图8(e),(f)可出看出态密度也增大，因此电导率随着磁场的增大而增大。在特定磁场下，随着无序得增加，能带展宽增加，输运弛豫时间减小。很自然地期待，体系需要更高的磁场来增大朗道能级间隔，从而抵抗这种减小趋势。因此电导峰将会随着无序的增加而移动到强磁场位置。我们注意到各向同性长程无序的定性结果与文献[107]一致，但定量结果不相同。这是因为高朗道能级辅助的背散射在以前的研究中被忽略，而这个机制可以起很大的作用。

4.讨论和结论

我们研究了强磁场下，长程无序和短程无序对 Weyl半金属体系的输运性质的影响。在弱的短程无序情况下可以得到单调的负磁阻效应，这是因为费米速度随着磁场增大而减小；而对于长程无序，磁阻可以是正的。对于沿着外尔点方向的弱长程无序，因为该方向的背散被压制，体系的弛豫时间很长。因此高朗道能级辅助的背散射很重要，这种情况下玻尔兹曼方程不再适用。弱的x-y平面的长程无序可以导致正磁电导率，这与玻尔兹曼方程的结果一致。对于强的长程无序情况下，这时候体系存在随着无序增加而向强磁场方向移动的电导峰。在量子极限下长程无序可以给出外尔半金属的正磁电导，但因为高朗道能级辅助的背散射这一原因，这样的结果并不能通过玻尔兹曼方程获得。总体来说，正磁电导有两个机制：第一，量子极限下，x-y方向的长程关联无序压制朗道能级内的散射； 第二，增加磁场时，相邻的两个朗道能级之间的间隔增大，导致高朗道能级辅助的背散射减小。我们的这些结果对最近的外尔半金属磁输运实验有重要的指导意义。

B.第一类外尔半金属中的无序与金属–绝缘体相变

1.背景与主要结果

在这一小节，我们将通过解析以及数值方法研究外尔半金属在无序下的相变特性。包括外尔点和费米弧在随机势散射下的稳定性以及无序诱导的金属绝缘体转变[37]。之前的研究都集中单个外尔点的性质[98−102]。理论上单个外尔点的体系即使在强无序条件下也不能发生安德森局域化。在实际外尔半金属材料中， NO-GO定理保证了手性相反的外尔点必须成对出现[59−60]，因此研究一对外尔点的局域化问题是十分必要的。因为当两个外尔点动量空间逐渐接近或强的谷（不同手性的外尔点）间散射使得体系无法定义手性，两个外尔点能够发生湮灭[103]。

我们主要研究了三维磁性外尔半金属体系，该体系可以通过沿z方向堆叠二维量子反常霍尔效应层获得[108]。我们考虑两个外尔点靠得很近得情况，即它们分别处于布里渊区边界或同时位于布里渊区中心。对前一种情况，我们发现外尔点对无序很敏感，两个外尔点在布里渊区边界混合最终湮灭并打开拓扑非平庸的带隙，从而引起外尔半金属到三维量子反常霍尔态的转变。而对于后一种情况，我们发现两个外尔点在无序存在下是稳定的。对于最初处于普通绝缘体状态的体系，带隙会随着无序的增加而减小并最终闭合，从而会在布里渊区中心产生一对相互排斥的外尔点，从而引发绝缘体到外尔半金属态的相变。虽然在动量空间严格分离的外尔点对弱无序是稳定的，但我们发现足够强的无序能够诱导出扩展的体态从而引发从外尔半金属相到三维扩散反常霍尔金属(diffusive anomalous Hall metal)[104]的转变。进一步增加无序强度，体系从三维扩散金属进入安德森绝缘体。我们通过局域化长度以及霍尔电导率[105−106]的计算，研究了无序诱导的多重相变，并且得到了外尔半金属在无序下的完整相图（见图10）。

我们考虑二带模型[108]：

其中tx,y,z,m0,mz是模型的参数，σx,y,z为泡利矩阵。波矢kx,y,z取值范围处于第一布里渊区内，Lx×Ly×Lz为体系尺寸，晶格常数a=1。H0可以看作量子反常霍尔体系沿着z方向的堆叠，tz,mz分别是层间耦合强度和交换场强度。从以上哈密顿量不难得到体态能谱：

其中 ∆z=mz−tzcoskz+m0(2−coskx−cosky)，注意到当H0关于σz的部分存在时，即因此H0(k)并不满足时间反演对称性，该二带模型只存在一对外尔点，是最简外尔半金属紧束缚模型。在对角项引入安德森无序，最终得到无序存在下的模型：

V1,2(r)在 [−W/2,W/2]之间均匀取值，其中W表示无序强度。

图9是干净外尔半金属哈密顿量H0的相图。当tz=0，层与层之间解耦。相图中有三个红色方块标记的临界点，当mz/m0=0，狄拉克点位于布里渊区中心(0,0)。 而对于mz/m0=−2,mz/m0=−4,狄拉克点分别位于布里渊区的边界 (0,π),(π,0)。 它们分出三个有带隙的相（正常绝缘体和两个量子反常霍尔效应相）。二维霍尔电导率为（左侧），e2/h（右侧）[109]。 当的情况下，体系为三维量子反常霍尔态，存在一个体带隙和完全量子化的霍尔电导率[108]。更重要的是，从图上我们不难发现存在一个外尔半金属相。相图几个相变边界为mz=±tz−4m0,±tz−2m0,±tz。外尔半金属拥有成对的外尔点，它们随着tz的变换在kz方向上分离。在对应的两个外尔半金属相，外尔点分别位于动量空间中的 (π,π,±arccos(mz+4m0)/tz),(0,π,±arccos(mz+2m0)/tz)以及 (π,0,±,arccos(mz+2m0)/tz),(0,0,±arccos(mz)/tz)。

图9.不存在无序时外尔半金属在tz/m0−mz/m0平面的相图，对应未引入无序的哈密顿量H0，本图片摘自文献。图片来自文献[37]。

图10.体系在W-mz平面的相图。图中实线是通过局域化长度获得的。实三角形是W=0的条件下，获得的两个相点。蓝色虚线为自洽玻恩近似的结果图片来自文献[37]。

不失一般性，我们把关注点锁定在−0.714＜mz/m0＜1.429，并且设定tz/m0= 0.479，即图 9中圆圈所标示区域。这个区域的外尔半金属相 (−1≤mz/tz≤1)，存在一对位于的外尔点。当外尔半金属经过普通绝缘体边界到三维量子反常霍尔效应边界,相应的，外尔点从中心(0,0,0)移动到布里渊区边界(0,0,π)。

图11.(a)-(f)表示归一化的局域化长度 Λ=λ(L)/L与无序 W 的关系。这里给了不同的几种 mz的参数。体系长度L=8,10,12,14其他的参数m0=2.1,tx,y,z=1图片来自 文献 [37]。

主要结论总结在无序相图中，如图10所示，体系存在四个不同的相（三维扩散反常霍尔金属相，外尔半金属相，三维量子反常霍尔相以及安德森绝缘体），和五个可能的无序诱导的相变，依mz从小到大分别为：(1)量子反常霍尔态–扩散金属–绝缘体，(2)外尔半金属–量子反常霍尔态–扩散金属–绝缘体，(3)外尔半金属–扩散金属–绝缘体，(4)绝缘体–外尔半金属–扩散金属–绝缘体，(5)绝缘体–扩散金属–绝缘体。相图的边界（实线部分）是通过数值方法计算霍尔电导率以及局域化长度获得的。我们发现弱无序下外尔半金属–量子反常霍尔态,外尔半金属–绝缘体相变的相边界与自洽玻恩近似的结果符合得很好。弱无序诱导的不同拓扑电子态之间的转变，扩展了拓扑安德森绝缘体以及无序和拓扑态相互作用物理机制的理解[32−34]。

我们通过局域化长度来研究安德森金属绝缘体相变并确定相变的边界。我们考虑三维棒状样品长度为Lz、宽度为Lx=Ly=L，其中x,y方向采用了周期性边界条件，样品的局域化长度λ(L)通过转移矩阵方法得到[110−112]。当重整化局域化长度Λ=λ(L)/L随着样品宽带L增加，说明体系电子存在拓展态，为金属相；相反如果Λ随着L的增大而减小，表示电子处于局域态，体系为绝缘相。如果重整化的局域化长度Λ不随着体系的尺度L而变化，它对应一个相变点。如图 11，我们计算了不同mz条件下的重整化局域化长度随着样品尺寸的改变。在图11(a)中，mz=−0.714m0，在弱无序下Λ随着L的增加而减小，体系处于绝缘的三维量子反常霍尔相。当W≈6的时候dΛ/dL=0，对应一个相变点。继续增大无序，重整化局域化长度满足dΛ/dL＞0，体系进入金属相，而这个区域具有非零的霍尔电导率（见图12(a)），因此我们认为这个区域为扩散金属相。进一步增大无序W，体态电子全部局域化，因此强无序下体系转变为安德森绝缘体。这个无序诱导的多重相变（量子反常霍尔态–扩散金属–绝缘体），这与多层量子霍尔体系以及三维Z2拓扑绝缘体中的相变特性是相似的[113−115]。

图10显示，量子反常霍尔态与外尔半金属的相边界向外尔半金属倾斜，这表明在量子反常霍尔相附近的干净的外尔半金属相（即：当外尔点在接近π时）对无序不稳定，它将随着无序的增加发生外尔半金属–量子反常霍尔态–扩散金属–绝缘体的一系列相变。这个意外的结果可直接从图11(b)mz/m0=−0.452和(c)mz/m0=−0.382中的局域化长度的标度行为看出来。为了理解这个结果，我们在本节第二部分通过做弱无序下的自洽玻恩近似来考虑无序诱导的能带重整化行为。有趣的是，无序对能带重整化最重要的影响是对拓扑质量mz的修正，这将会增加能带的反转，从而引起两个外尔点在布里渊区边界相互“吸引”。当两个外尔点在布里渊区边界相遇时，这对外尔点将湮灭，同时体系会打开一个非平庸的能隙，从而导致外尔半金属相到三维量子反常霍尔相的转变。我们后面部分将会发现这个相变可以由费米弧的消失和体系产生整数化的量子霍尔电导率的现象来表征。通过类似上面的方法，我们对图10中外尔半金属和绝缘体相进行分析，发现另一个奇特的结果。当外尔半金属相接近于绝缘体相的时候，由于无序对mz的重整化使得外尔点相互“排斥”并远离，因此布里渊区中心的两个外尔点对弱无序很稳定。这就解释了为什么图11(f)中局域化长度Λ在W≈3.3附近表征出一个相变临界点。这个标度行为肯定了上面的相变过程。因此，当一对具有相反手征的外尔点在足够远离布里渊区边界的时候，它们对弱无序下的谷间散射是稳定的。值得注意的是，在足够强的无序下，我们发现了一个从外尔半金属到扩散金属的直接相变。这就是相图中外尔半金属–扩散金属–绝缘体和绝缘体–外尔半金属–扩散金属–绝缘体相变的由来。这种相变是由强无序下体系突然出现体态导致的。因此，从图 11(d)～(e)中的第一个临界点和(f)中第二个临界点两边dΛ/dL＞0的行为中，我们可以看到两个金属态之间的不寻常相变。实际上，外尔半金属和三维扩散金属可以通过霍尔电导率的量子化行为加以区分。

对于三维外尔半金属，对给定的kz， 它在二维xy平面的量子化电导率满足，整体的电导率[117]为其中为阶跃函数。求和化积分以后表示外尔点到布里渊区中心的距离。从这里不难看出，当两个外尔点在布里渊区边界的时候，两个外尔点之间的距离最大，这时有最大霍尔电导率σxy=e2/h。

图12.(a)-(f)平均的霍尔电导率σxy与无序W 的函数。样品大小30×30×8。mz已在图中标出。图片来自文献[37]。

图12(a)表示，三维量子反常霍尔态有一个完全量子化的电导平台σxy=e2/h直到W≈6.0体系进入扩散金属态，对应地体态转变为拓展态，此时σxy的量子化不复存在并且随着W的增大而减小，同时这个区域存在普适电导涨落，这与图11(a)的结果一致。在图12(b)～(c)中，体系最先处于靠近三维量子反常霍尔态的外尔半金属相，这时因为两个外尔点不在布里渊区边界并且在布里渊区分离，根据前面电导率的定义，产生σxy=7e2/8h分数化的霍尔电导平台。继续增大无序，这对外尔点到达布里渊区边界并湮灭掉，这时费米弧变成一系列的边缘态，霍尔电导率达到三维量子反常霍尔态的最大霍尔电导率σxy=e2/h。继续增大无序，体系进入扩散金属态，并最终进入到安德森绝缘态。图 12(d)～(e)显示，体系并没有达到最大霍尔电导率。即外尔点并没达到布里渊区边界并湮灭，而是直接进入了扩散金属态，即体系发生了从外尔半金属–金属的相变。图12(f)显示，随着无序的增大，体系在W≈3.3的时候带隙闭合，从普通绝缘相(σxy=0)进入到外尔半金属相,并且随着无序的增大，两个外尔点之间的距离增大，电导率逐渐增加，但是两个外尔点还未达到布里渊区边界，体系就从外尔半金属相进入扩散金属相。我们需要强调，霍尔电导计算结果与局域化长度的结果在定量上也是非常一致的。

2.自洽玻恩近似

在玻恩近似下，我们把无序对体系的影响考虑成格林函数的自能修正：

图13.不同无序强度W 和mz的情况下自洽玻恩近似获得的能带图。色散关系对应准三维样品，其中z方向是无限长的，Lx=Ly=14a并选取周期性边界条件。重整化后的质量z通过Eq.(75)得出。红色点线标记两个外尔点的位置。其它参数已在图中标出。

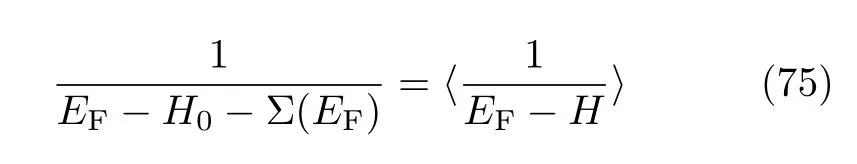
其中H0是未引入无序的哈密顿量，而H为引入无序后的哈密顿量。〈···〉表示对所有无序的系综平均，可以把无序导致的自能修正分解为：

从而获得重整化的质量和费米能：

因为零阶玻恩近似的结果是把所有能级移动一个常数，因此我们需要考虑更高阶的玻恩近似的费曼图修正。自洽玻恩近似[34]与一阶玻恩近似的区别在于，散射后的传播子采用费曼图修正后的结果，而玻恩近似的传播子为自由的传播子，在这里对应未引入无序哈密顿量的传播子。这样可以得到自洽玻恩近似的表达式：

其中a=1,tx,y,z=1,m0=2.1,EF=0。很容易验证ℜΣ0=0,因此费米能并没有发生重整化，但是因此质量发生了重整化。

如图13，在W=0的情况下，我们选取了mz=[−1.2,−1,−0.8,0.8,1,1.2]， 引入无序以后mz重整化后为，其中m0=2.1。正值与负值分别表示靠近外尔半金属–绝缘体和量子反常霍尔态–外尔半金属的相边界。整个结果与我们之前的分析（图10～图12）是一致的。

总的来说，我们研究了具有两个外尔点的外尔半金属在无序下的相变特性，最终首次获得了外尔半金属在无序下的完整相图。在弱无序下，当外尔点在布里渊区靠近的时候，如果两个外尔点处于布里渊区边界，那么这对外尔点将会在边界湮灭，发生外尔半金属到三维量子反常霍尔态的相变。同时无序也可以在布里渊区中心闭合体带隙并产生一对外尔点，从而发生从绝缘体到外尔半金属的转变。强的无序可以使体系发生从外尔半金属到扩散金属的相变。这一结果对于具有多对外尔点的外尔半金属体系的研究具有重要的指导意义。

C.第二类外尔半金属在无序条件下的相图

1.第二类外尔半金属背景简介

上面的两个工作主要集中在第一类外尔半金属体系中，本小节我们研究第二类外尔半金属在无序下的相图。我们首先简单介绍一些关于第二类外尔半金属的背景。在第一类外尔半金属被实验验证后不久，物理学家就提出了一类破坏洛伦兹规范的外尔半金属体系，它的哈密顿量形式为：

其中σx,y,z是泡利矩阵，而σ0是个2×2的单位矩阵，α是可调节的参数。kxσ0的作用使得外尔半金属的哈密顿量的洛伦兹不变性被破坏，这里我们给出一个简单证明。

洛伦兹不变性可以理解为在四维坐标变换下（变换不能改变时间演化方向和度规的号差）实验观测到的物理规律是相同的(physics looks the same)。我们构造拉氏密度

因为体系的自旋为ħ/2，所以ϕ为旋量场（旋量与矢量虽然可以具有相同的生成元，但是基底不同，旋量选择双群表示，因此它们在洛伦兹变换下的结果不同），我们可以将旋量场看做标量场对L进行洛伦兹变换，虽然泡利矩阵原本与坐标无关，现在需要将其看作矢量进行洛伦兹变换。这样的过程与将旋量场做洛伦兹变换，而泡利矩阵与坐标无关所得到的结果一致。洛伦茨变换的结果为：

其中为洛伦兹变换的群表示。变换后x→x′，因此泡利矩阵和与偏微分算符对应的坐标都发生改变。考虑到洛伦兹变换满足因此得到：

从上式，可看出洛伦兹变换只是对坐标作了改变，但是整个拉氏密度的形式与系数都没有发生变化。考虑到测度在洛伦兹变换下也是不变的，因此第一类外尔半金属的哈密顿量满足洛伦兹规范不变性。下面证明i∂xσ0会破坏洛伦不变性，同理该项在变换下的结果为：

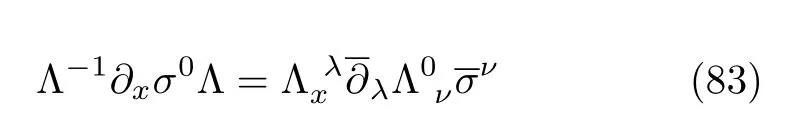
变换后得拉氏密度与洛伦兹变换的表示有关，因此洛伦兹规范被破坏。这里需要强调的是，只要kxσ0这一项不为0，即外尔锥只要发生倾斜，洛伦兹规范就不复存在。

图14.(a)表示第一类外尔半金属的能带色散关系。(b)外尔锥存在倾斜，但还是第一类外尔半金属，此时洛伦兹不变性已经被破坏。(c)外尔锥倾斜很大，使得外尔点的态密度不再是0，而具有一个有限值。体系称为第二类外尔半金属。

真空必须服从洛伦兹规范，这是相对论的要求，因此哈密顿量 Eq.(77)描述的粒子在真空中是不可能存在的，但是凝聚态材料中准粒子激发并不需要满足洛伦兹规范。当α＞1，这个哈密顿量就是描述第二类外尔半金属中准粒子激发的低能有效哈密顿量。第二类外尔半金属在理论提出后[20,116]很快就被实验验证[21]，其中可能是第二类外尔半金 属 材 料 有 MoTe2[43,118]、WTe2[119]、LaAlGe[120]、TaIrTe4[121]、PtTe2[122]以及 Ta3S2[123]。

洛伦兹变换并不能帮我们区分第一类外尔半金属以及第二类外尔半金属，这是因为第一类外尔半金属的外尔锥倾斜以后仍有可能是第一类外尔半金属（如图14(a,b)所示），只有当外尔锥倾斜达到一定程度，W外尔锥发生了倾倒，此时外尔点具有了有限态密度，体系才是第二类外尔半金属（如图14(c)所示）。

下面我们采用转移矩阵以及自洽玻恩近似方法计算了存在倾斜项的第一类外尔半金属 (WSM1)以及第二类外尔半金属 (WSM2)在无序影响下的相变特性[39]。

2.模型和干净样品的相图

倾斜外尔半金属的哈密顿量可以写成如下形式H=H0+Htilt。其中H0就是第一类外尔半金属的哈密顿量

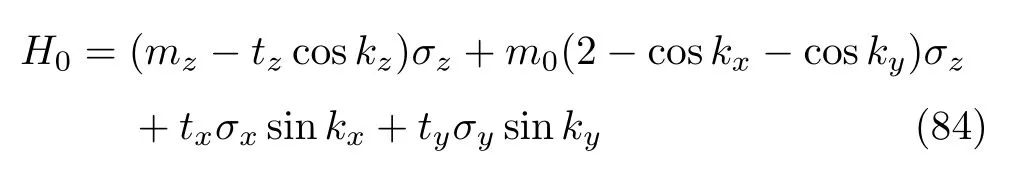
倾斜项[124]为

其中at,bt都是实数，而I2×2是单位矩阵。

图15.存在倾斜项的外尔半金属在无序为零时的相图，参数为tx=ty=tz=1,m0=2.1。图片来自文献 [39]。

可以验证这个体系H的时间反演以及空间反演对称性都被破缺。H0具有空间反演对称和粒子–空穴对称性，但前面已经证明H0的时间反演对称被破坏。考虑哈密顿量Htilt，非零的at破缺空间反演对称性，使得Weyl点不在同一个能量。而非零的bt破缺粒子–空穴对称性。因此当at̸0,bt0我们可以获得两种不同的类型的外尔点，一个外尔点对应第一类外尔半金属，而另外一个手性相反的外尔点对应第二类外尔半金属。但此时体系非常复杂，不利于相变性质的研究。所以这里只关注at=0的情况，此时哈密顿量H具有空间反演对称性，两个外尔点不仅属于同一类型，而且具有相同的能量。

同上一节类似，我们引入无序

均匀分布于[−W/2,W/2]，W表示无序强度。

图15为干净样品的相图当mz＜−tz，两个外尔点在布里渊区边界湮灭，体系进入三维量子反常霍尔态。当mz＞tz的时，两个外尔点在布里渊区的中心湮灭，体系进入普通绝缘态。而处于−tz≤mz≤tz的时候，体系存在两个在空间分离的外尔点。为了区分第一类外尔半金属与第二类外尔半金属，我们分析体能带的群速度[125]，最终得到−1＜bt＜1对应第一类外尔半金属，|bt|＞1对应第二类外尔半金属。

图16展示体系能带结构E-kz随着倾斜项bt的演变。当bt=0.95的时候，虽然外尔锥已经倾斜（如图14(b)），但是并没有转变成第二类外尔半金属。但是bt＞1时，外尔锥的边界跨过费米面，这时体系为第二类外尔半金属，该结果与图15是一致的。

3.转移矩阵的数值结果

图16.能带结构 E-kz随倾斜项的演化，其中 kx=ky=0,at=0,mz=0.190m0，bt的数值已在图中标出。可看出bt=1是第一类和第二类外尔半金属的分界点。

这里同样采用转移矩阵计算了重整化的局域化长度Λ=λM/M，其中Mx=My=M。 随着样品宽度M的增大，如果Λ也增大，体系处于金属态，反之体系处于绝缘态。

同上一节，我们通过分析图17给出的转移矩阵的结果，对应地获得了存在倾斜项的外尔半金属在无序下的完整相图（见图 18(a)）。 对于小的bt，如bt=0.2,0.4,0.6，当W=0的时，对应第一类外尔半金属。增加无序W，系统依次经过三维量子反常霍尔相、扩散金属(diffusive metal)相以及普通绝缘相。中间的三维量子反常霍尔相在bt=0时难以被转移矩阵的结果清晰表征，因此在上一节的工作中可能被忽略了，这个相在最近的一个工作中被强调[126]（at=bt=0的情况下）。有意思的是，我们发现这个介于外尔半金属和扩散金属中间的三维量子反常霍尔相在bt̸0的时候变得非常明显，因为dΛ/dM随着倾斜强度bt的引入而变得更大了（如图17(a),(b)）。这个中间相可以理解为杂质引起的谷间散射使得两个谷合并，因此可以看成三维量子反常霍尔态的延伸，上一节中的三维量子反常霍尔态和第一类外尔半金属的相边界可能需要修正。

图17.不同bt下，重整化局域化长度Λ关于无序强度W 的曲线。插图着重展示相变点附近的细节吗，其它参数与图16一致。图片来自文献[39]。

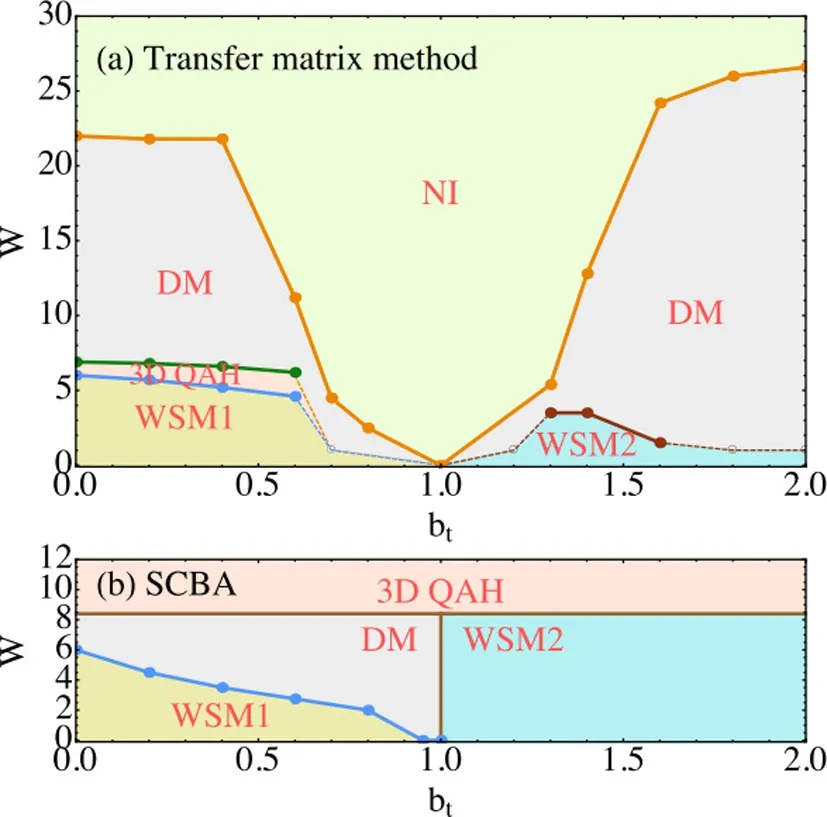
图18.相图 bz-W；kx=ky=0,at=0,mz=0.190 m0。(a)转移矩阵法获得的完整相图。其中实线与实点对应从转移矩阵获得的相边界，而虚线以及空心圆圈对应可能的相边界（这些区域点的局域化长度太长了，数值不能获得准确结果）(b)自洽玻恩近似获得的相图。图片来自文献[39]。

对于更大的倾斜度bt=0.8（图 17.(c)），只有从第一类外尔半金属–扩散金属–绝缘体的相变被观测到。但是三维量子反常霍尔态可能仍然存在于第一类外尔半金属与扩散金属这两个相之间。这是因为对于小的无序强度，Λ很大(≈102)且收敛性很差，因此转移矩阵法很难给出准确的结果，因此采用虚线以及空心圆圈来表示这些区域。总体来说，当0＜bt＜1的时候，随着倾斜强度bt的增加，安德森转变（金属–绝缘体转变）需要的无序强度越来越弱。

当bt≈1的时候，不管无序强度多弱，金属相都消失（如图17(d)），相应的Λ也非常的小。 也就是说，当bt趋向于1的时候，小的无序也能诱导出绝缘体相变。这是因为其中一条能带近乎是平的，这导致一个无限大的有效质量，按照安德森无序理论，这条平带在非常弱的无序下即发生局域化。注意到大动量散射在这个模型中是被允许的，因此另外一条非平的能带在无序诱导的谷间散射下与平带耦合，从而使得非平能带中的电子也进入局域态。因此在真实材料中，第一类外尔半金属和第二类外尔半金属的相边界也许是没有物理意义的，因为很弱的无序就能破坏外尔半金属相。

当bt=1.3，1.4以及1.6，转移矩阵的结果显示两个金属相出现在相变点两侧（如图17(e)Wc≈3.5两侧）。因为在W=0的时，体系必须是第二类外尔半金属，因此在弱无序下的结果是第二类外尔半金属相，而较强无序下的结果是扩散金属相。而对于小的bt，比如bt=1.2或者大的bt=1.8，2，重整化局域化长度Λ在弱无序下很大。因此在这些区域不能采用转移矩阵法获得精确的结果。此外没有数值证据表明在扩散金属–第二类外尔半金属之间还存在三维量子反常霍尔相，我们认为对于第二类外尔半金属，中间的三维量子反常霍尔相应该是不存在的。因为第二类外尔半金属在费米能有非零的态密度，两个外尔点之间的散射不像在第一类外尔半金属中那么重要了。有意思的是，我们发现同等条件下（如图17(a),(f)中W=10时），第二类外尔半金属的局域化长度也要比第一类外尔半金属的局域化长度大一个数量级。一方面第二类外尔半金属比第一类外尔半金属在无序下输运性质更好，有利于它的器件应用；另外一方面，对于第一类外尔半金属输运弛豫时间与量子弛豫时间比值很大（见最后一节），由于第二类外尔半金属比第一类外尔半金属有更长的局域化长度，我们预期该比值会更显著，这个效应能被当前实验观测到。

图19.(a)-(b)自能对角部分的虚部 ℑ[Σ0]±ℑ[Σz]与无序强度 W 的关系。(c)费米能附近的态密度与无序强度 W 的关系。(d)-(e)自能的实部 ℜ[Σ0]与 ℜ[Σz]与无序强度 W 的关系。ℜ[Σ0]会移动费米面的位置，ℜ[Σz]会重整化拓扑质量 mz， 能近似采用ℜ[Σz]=−0.02W2拟合。图片来自文献[39]。

4.自洽玻恩近似

为了更好的理解第二类外尔半金属在无序下的相变，我们通过自洽玻恩近似计算了体系的自能修正。如图 19(a),(b)，自能的虚部决定准粒子的寿命，ℑ[Σ0]±ℑ[Σz]都小于 0，并且随着bt以及W的增大都是减小的。这表示在无序下的外尔半金属有两种准粒子，他们的寿命均随着倾斜强度以及无序强度的增大而减小。费米能的态密度与Σ0的虚部有关， 其表达式为：

当bt＜1时，费米面的态密度是零，这时候两个外尔点都是第一类外尔点，与之前的分析一致。存在一个特定的无序强度Wcl(如图 19(c))，当W＜Wcl的时候，体系在费米面的态密度仍然为0，而当W＞Wcl的时候，费米能级有非零的态密度，体系进入扩散金属相。根据Wcl我们得到了图18(b)中的蓝色实心圆以及蓝色实线。这条线区分了第一类外尔半金属与扩散金属相，它定性来看与转移矩阵给出结果趋势上一致，但定量上并不相同，而且自洽玻恩近似也不能得到图18.(a)的三维量子反常霍尔相。而对bt＞1，由于第二类外尔半金属在费米面上也具有非零的态密度，因此自洽玻恩近似不能给出Wcl，自洽玻恩近似也不能给出第二类外尔半金属与扩散金属的相边界。

接着我们研究自能的实部，因为ℜ[Σ0]与动量k无关，它仅仅移动费米面。因为电子空穴对称，当bt=0的时候 Σ0也为零。对于非零的bt，理论上费米能级发生移动，使得体系获得有限的态密度(bt＜1)，但从图19(d)可看出这种移动并不明显，我们推测图19.(c)描述的物理机制在外尔半金属到扩散金属的相变中占据主导地位。与此同时ℜ[Σz]是负的，并且随着无序强度W的增加而减小，说明无序的作用总是趋向于使能带反转得更厉害，理论上这种趋势会使得体系在Wc2≈8.4从外尔半金属转变为三维量子反常霍尔态（如图 18(b))）。但通过比较图 18.(a)和 (b),我们发现转移矩阵的结果与自洽玻恩近似的结果并不自洽，这是因为自洽玻恩近似只适用于弱无序的情况，它给出的三维量子反常霍尔效应在转移矩阵的结果中并没有体现出来，而且自洽玻恩近似中也不能预测普通绝缘体相。

玻恩近似常被用来研究无序体系的相变性质，通过以上具体的研究，我们给出了玻恩近似的适用范围，这对后续的无序体系物性研究有一定的指导意义。

IV.外尔半金属中拓扑IMBERT-FEDOROV效应

A.背景

图20.入射光线与出射光线的中心不在同一个位置，图中标出了Imbert-Fedorov位移DIF以及Goos-Hnchen位移DGH。

外尔半金属的能带具有三个方向的线性色散关系，与光学中频率波矢色散关系完全类似，一些新奇光学现象可能在外尔电子体系出现，在本节我们研究了这一问题。我们初中开始接触的几何光学告诉我们，入射光、反射光与折射光在同一平面，且相交于同一点。这是因为几何光学考虑的是平面波的光，而实际情况下，携带信息的应该是光束。有限大小的光束在平面内的反射的情况就相当复杂了。这里我们介绍光束中心在平面内以及平面外的位移。

Goos-Hnchen位移:早在 17世纪，牛顿就推测光束中心在介质表面反射的时候会有一个在入射平面内的位移。两个世纪之后Goos与H¨anchen两人成功测量出了这个面内位移，称为 Goos-H¨anchen(GH)位移[128]（如图(20)中的DGH）。由于GH位移特征长度是亚波长，所以近年来GH位移在光波导以及微波腔体有重要应用。理论上，GH位移已经在多个层次上得到了解释，并且拓展到其他光学体系。原因在于，GH位移的本质是由于光的波粒二象性导致，由于自然界所有已知粒子都具有波粒象性。所以GH位移不仅存在于光子的反射过程中，也存在于原子[129]、中子[130]、电子[131]等体系。GH位移亦存在于石墨烯等极端相对论材料的电子反射过程中[133]。

Imbert-Fedorov位移:另外一种超越几何光学定律的位移是 Imbert-Fedorov(IF)位移，这个位移是指反射平面之外的横向位移（如图 20中的DIF）。与GH位移简单的物理起源相比，IF位移的物理起源则相对复杂甚至引起了很多争论。最开始是 Fedorov和 Imbert通过波印廷矢量来来讨论 IF位移的存在性[132,134]。之后 在 1965年，Schilling首次利用平面波叠加和干涉原理给出 IF位移的表达式的完整形式[135]。在 1987年，Fedoseyev和 Player发现 IF位移与光的动量守恒有关[136]。1992年，Liberman和Zel’dovich通过引入了光的自旋轨道耦合效应[137]，重新推导出了 IF位移和 Schilling公式。2004年，Onoda等人把 IF位移看作光子的霍尔效应，通过几何贝里相位将 IF位移推导出来[138]。最近，Bliokh等人给出了完整的理论办法推导出IF位移，并且预言了角度 IF位移[139]。这个理论于2008年在实验上被Hosten和Kwiat验证。Hosten等人利用弱测量办法成功测出了左旋光和右旋光具有相反的Imbert-Fedorov位移[140]。迄今所有的关于IF位移的争议都已经消失，而且GH位移和IF位移可以统一于波包在反射过程中发生形变这一框架下。GH位移在石墨烯中已经理论预言，但由于石墨烯是二维体系，因此不存在IF位移。为了研究极端相对论条件下IF位移，我们希望在三维体系即外尔半金属体系中寻求这一效应[40]。

B.weyl半金属体系中的 IF位移

为了研究GH位移以及IF位移，我们利用外尔半金属体系构造一个pn结[40,141]，哈密顿量满足如下形式

在x=0存在跃变的势垒。我们用体系的本征态构造高斯波包，波包从x＜0入射到x=0平面，产生反射。入射高斯波包满足：

其中x,y)为高斯分布函数。波包展宽为 ∆ks,并且存在最大值位置，即波包中心波包表达式中的ψin(k,r)满足定态方程Hψin=Eψin，在x＜0求解的结果

有同理构造反射波包：

而ψre(k,r)只需要将kx→−kx,α→π−α得到：

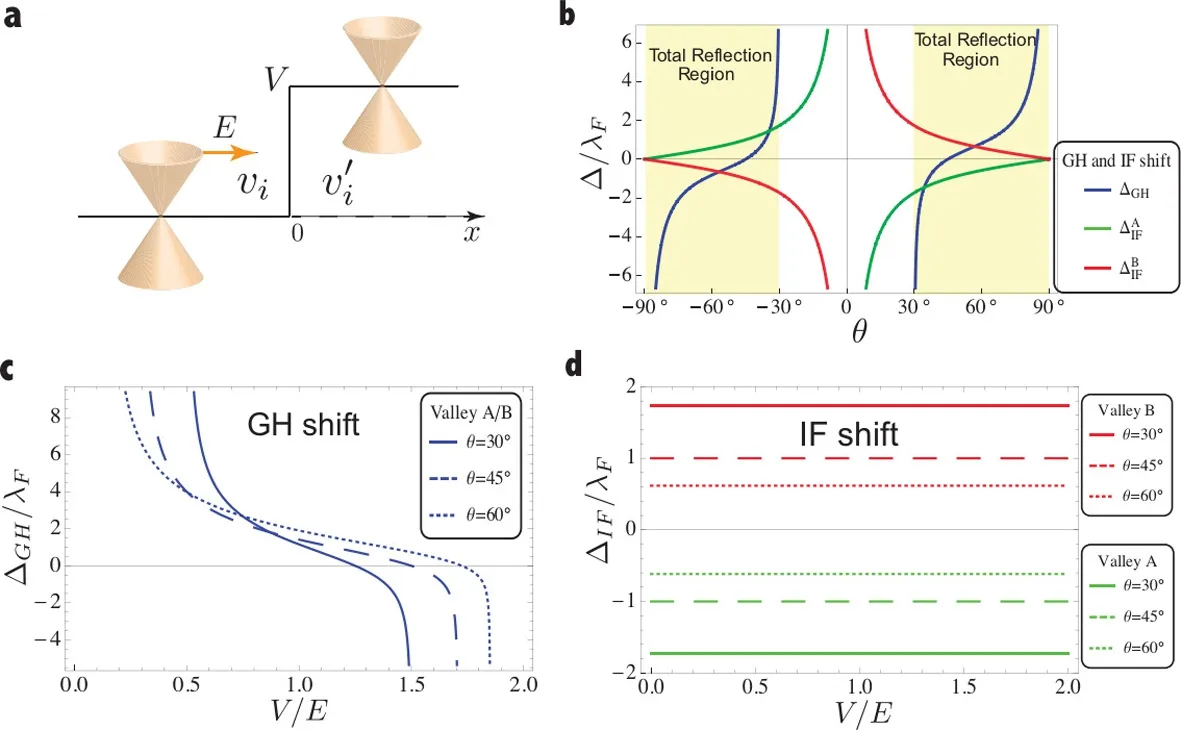
图21.(a)外尔半金属pn结示意图。(b)不同手性外尔费米子的GH位移和IF位移与入射角的依赖关系。图中的黄色区域对应全反射区域。λF=ħνi/E为费米波长。(c)(d)不同入射角θ=30,45,60情况下,GH位移(c)和IF位移(d)随着界面势能V的依赖关系。图片来自文献[40]。

从Eq.(90)和Eq.(91)可看出，因为反射相位的存在，反射时波包的叠加情况会发生改变。由于这个原因反射波包的中心会发生位移。为了计算波包中心的位置，我们采用stationary phase method或者把波包的积分积出，高斯波包的中心位于波包函数的最大值位置。

stationaryphasemethod：对于F(x)=∫dkf(k−k0)eiα(k,x)，F(x)的最大值在x0,并且满足 dα(k,x0)/dk|k0。

这里采用高斯积分可以计算入射以及反射波包中心的位置分别为：

其中下标±表示上旋量以及下旋量，同理反射波包的中心位于：

相减我们可以得到在z方向以及y方向的位移得到：

图22.(a)正的GH位移，以及手性依赖的IF位移。(b)负的GH位移，以及手性依赖的IF位移。图中红色绿色表示两个不同的手性锥。图中GH位移可以调节，但是IF位移是手性依赖的。图片来自文献[40]。

其中α=arctan(νyky/νzkz)，而反射相位仍然未知，因此需要求解反射相位。我们这里主要考虑全反射情况|r|=1，x＞0区域的波函数必须是指数衰减的。根据ψin+ψre与右侧衰减波函数的连续性条件，因为哈密顿量只有一阶导数，所以只需考虑波函数在x=0连续即可得到：

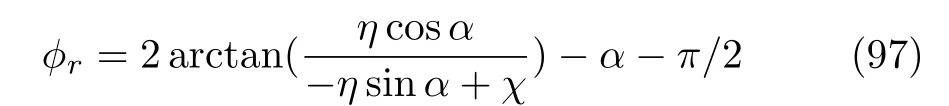
相位表达式中其中按照波函数上下旋量的权重，我们得到方向对应GH位移，z方向对应IF位移。经过简单计算，最终获得了GH位移以及IF位移的表达式：

其中是手性的定义。选择，因此β=γ=1。从方程(90)和(91)我们不难发现：第一，GH位移依赖界面势能V，而IF位移与界面势能V无关，即IF位移对界面不敏感。第二，GH位移与外尔费米子的手性无关，而IF位移依赖于外尔费米子的手性。

图21(c)显示 GH位移大小依赖于势能V，并且GH位移的正负可通过V调控。图21(d)显示IF位移与V无关，但却是谷依赖的（这里谷等价于Weyl费米子手性）。谷依赖的IF位移提供了新的方法去实现谷电子学（如图22）。

C.半经典运动方程

上一小节告诉我们，IF位移与界面的具体情况完全无关，究其原因它是一个拓扑效应，下面我们给出它的拓扑起源。在第二小节，我们得到了外尔半金属具有非零的贝里曲率，根据文献[77]，贝里曲率结合动量的改变会提供一个反常速度项：

由于x方向界面势能在x=0的改变，x方向动量发生改变，结合y方向的贝里曲率Ωy，从而导致z方向的位移：

进一步令νx=νy=ν||,νz=ν⊥，于是得到的IF位移为

从上式不难看出，半经典理论得到的IF位移与在相同条件下的全量子计算结果（Eq.(97)）一致。在上述推导中，我们只利用了全反射时x方向动量大小相等方向相反和外尔点的贝里曲率有磁单极的形式，这两个性质是普适的，与具体材料细节无关，因此IF位移是一个拓扑位移。

D.IF位移导致的反常速度

我们考虑如图23(a)所示的外尔半金属三明治结构，在区域II注入外尔费米子。三个区域的电势也在图a的下图中标出。如果体系关于x=0中心对称，GH位移在左右两侧是同向等大的，而IF位移则在两个交界面等大反向。要得到IF位移的效应，必须要破坏体系关于中心的镜面对称。我们使三个区域沿着z方向的费米速度不同，这样很显然破坏了镜面对称性。外尔费米子在区域II来回多次反射后，GH位移与IF位移会在x，y方向积累，形成反常速度：

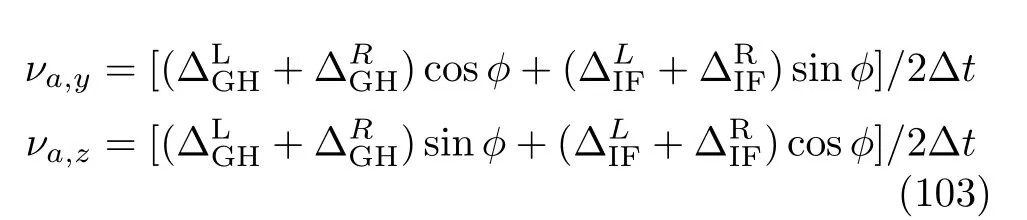
其中表示两次反射之间的时间差。入射引起的正常速度为νn,y=νsinθcosϕ,νn,z=νcosθsinϕ,总的速度为νt,y(z)=νn,y(z)+νa,y(z)，而且IF引起的反常速度总是垂直于外尔费米子的传播平面。

给定入射角，可以计算最终的位移。不考虑反常速度，到达区域II底部的时间为T0=h/νn,z,考虑反常速度后T1=h/νt,z，最终在y方向产生的位移为：

图23.(a)外尔半金属三明治结构示意图。参数设为费米能E=100 meV，势能差V=150 meV，高度h=10µm，三个区域 z方向的速度 νIz=νL=1.2×106m/s,νIIz=ν=106m/s,νIIIz=νR=0.8×106m/s其它方向速度为 106m/s。除正常速度外，体系中还存在GH位移和IF位移引起的反常速度。(b)Weyl费米子在区域II的运动轨迹，对应黑色箭头。电子由透射电子显微镜注入，注入角为θ，h是结构的高度，d是中间区的宽度，θ=30,d=50 nm。通常情况下运动轨迹处于平面ABMN,但是由于IF移动，两个谷的运动平面分别位于ABRS和ABPQ，在空间分离。(c)GH位移引起的反常速度与入射角度的关系。(d)IF位移引起的反常速度与入射角的关系。(e)GH位移与IF位移引起的总的反常速度。(f)反常速度在空间引起的正负位移SN,QN。图片来自文献[40]。

由上式，我们最终得到图23(c)～(f)。实线表示y方向，虚线表示z方向。GH位移与谷无关，而IF位移中红色与绿色分别对应两个不同的谷。因此最终导致总的反常速度也是谷依赖的（图23(e)）。而两个不同谷的费米子最后会在空间分开积累（如图23(f)），使得制作谷电子器件成为可能。如图24(f)所示，我们采用这个结构构造了谷器件，(a)(b)是不考虑GH位移和IF位移时的谷积累，可以看到两个谷在空间的同一个位置，而当引入GH和IF位移后如图24(c)～(e)所示，两个谷的积累效果在空间被分开。

这里必须指出，IF位移还可以帮助判断费米弧结构是否存在。我们发现Weyl半金属与真空的交界面处入射的外尔费米子是不存在IF位移的（详见[141]）。由于IF位移需要手性能够被很好得定义（它与手性密切相关），这就表明了在外尔半金属与真空交界面上存在两种手性外尔费米子的混合模式，费米弧表面态是连接两种手性费米子的通道，因此IF位移可以充分体现费米弧存在性的物理本质。我们前文也提到了，判断外尔半金属最重要的依据就是费米弧和线性能带，而对于磁性材料的费米弧和线性能带很难直接通过角分辨光电子能谱来表征。但是通过这一方法，我们只需要观测体系与真空交界面不存在IF位移，而同种材料构造的pn结存在手性依赖的IF位移，这就能证明手性费米子与表面费米弧的存在。

此外，IF位移的起源于贝里曲率。贝里曲率虽然是规范不变量，因此从理论上来说是能够被测量的，但是一直以来鲜有可行的实验方案去探测凝聚态材料的贝里曲率。通过IF位移的拓扑起源，我们可以通过量化的关系

得到材料中的贝里曲率。因此这使得在实验上探测贝里曲率这一重要物理量成为可能。

E.总结

本节我们把光学中的概念 Goos-Hanchen位移和Imbert-Fedorov位移应用到了拓扑半金属体系。我们通过全量子力学方法得到了外尔费米子波包在p-n结界面存在势能可调的Goos-Hanchen位移和拓扑保护的Imbert-Fedorov位移。同时，我们通过半经典波包动力学方程推导出了Imbert-Fedorov位移，并得到了相同的结果。我们发现Goos-Hanchen位移与外尔费米子手性无关，而Imbert-Fedorov位移却依赖于外尔费米子手性，同时我们发现Imbert-Fedorov位移可导致谷极化效应。另外，我们提出Imbert-Fedorov位移可应于直接探测体系的贝里曲率。最后我们介绍了外尔费米子在外尔半金属与真空交界面处反射过程，我们发现外尔费米子会在反射过程中发手性混合，这从一个新的角度说明了外尔半金属表面态费米弧存在的原因。最近外尔半金属IF位移的概念得到了进一步推广,具体可参考文献[142-145]。

图24.(f)采用IF位移构造的谷器件示意图；(a)(b)表示不考虑GH位移和IF位移的时候，两个不同手性费米子在空间的积累，颜色越深表示积累的密度越高。(c)-(e)表示考虑GH与IF位移以后，两个谷的外尔费米子在空间的积累，可以看到两个谷的载流子在空间被分开。图片来自文献[40]。

最后我们比较光学中的IF位移与外尔半金属中IF位移。虽然外尔半金属中的IF位移和光学中IF位移都是三维效应，但是二者存在许多显著的差异：（1）光学中的IF位移来自于解麦克斯韦方程组，而外尔半金属中的IF位移来自于解外尔方程，不同类型的方程自然会给出不同的结果。（2）在光子自旋霍尔效应中，霍尔电流是光子的自旋流，而外尔半金属IF效应中，霍尔电流是手性电子流。（3）光子的偏振（自旋）并不是好量子数，并且在反射过程中改变。然而IF效应中手性则是个好量子数，并不会在反射过程中发生改变。这会使得外尔半金属中的IF位移和光子的IF位移差异明显。例如：垂直入射时，由于光子在反射过程中偏振方向反号，导致光子的IF消失。与之对比，由于手性在反射过程中保持不变，导致垂直入射情况下外尔半金属中的IF位移达到极大值。

V.外尔半金属中单杂质波包散射效应

A.背景

在固体材料中，引入电场会加速电子产生随电场增大而增大的漂移速度。由于杂质缺陷的原因，这个漂移速度必然存在一个上限虽然继续增大电场电子漂移更剧烈，但是与杂质的碰撞与散射也加剧，两者相互竞争，最终达到稳定，因此得到:

表I.各种拓扑半金属中超高迁移率，表格来自文献[149]。

图25.(a)外尔费米子波包在杂质下的散射示意图。b为散射碰撞因子，θ,ϕ对应入射方向的参量。(b)手性保护位移在不同散射角度下与费米能的关系。(c)手性保护位移∆ch在波包散射后出现，红色箭头表示手性为C=−1的波包出射方向。(d)手性为C=−1的波包出射动量空间分布图，沿 z方向看，出射动量分布构成一个螺旋图，半径对应手性保护位移的大小。图片来自文献[146]。

其中τt是输运弛豫时间，τt越大，初始动量被弛豫的时间越长，达到稳态时漂移速度越大，杂质散射的作用越弱。迁移率的定义为，这个公式表明输运弛豫时间越长，杂质散射越弱，迁移率越高。下面我们定义一个新的物理量，量子弛豫时间τq。输运弛豫时间可认为是电场方向的动量被碰撞弛豫掉的平均时间。量子弛豫时间是电子与杂质发生两次碰撞所经历的平均时间，它可通过能级的展宽来估算。单电子近似下，量子弛豫时间与输运弛豫时间都可以通过散射界面得到：

νf,ni分别表示费米速度与杂质浓度。Ω表示立体角，σ(θ,ϕ) 是微分散射截面。Rτ=τt/τq是一个与输运密切相关的重要物理量，一般而言，Rτ大表明载流子经过多次碰撞后仍保持原来的运动方向，电场对载流子加速效果明显，迁移率高。如果微分散射截面是常数的话，多数情况下，这两个时间是一个量级的，例如在普通二维电子气和石墨烯体系中Rτ=2。但对于高迁移率GaAs二维电子气等，因为载流子层与杂质层在空间上分离，使得Rτ可以达到10～100这样地量级。

最近几年，大量实验数据表明拓扑半金属体系Rτ达到了 104量级[147]，如表 I所示，相应的拓扑半金属（外尔半金属）的迁移率非常高，达到了107cm2.v.s−1。二维电子气高迁移率来源于载流子与杂质层的空间分离，为什么外尔半金属体系的载流子与杂质在空间上是重叠的，却会有如此高的弛豫时间比值和载流子迁移率？由于迁移率是材料最重要的指标，是材料在电子器件应用方面的基础，因此外尔半金属的高迁移率问题是拓扑态研究的核心问题之一。我们在这一部分提供解决该问题的新思路[146]。

我们考虑Weyl半金属体系。波包被单杂质的散射，如图25(a)所示，体系哈密顿量为：

B.手性保护位移

νij是速度参量，代表ki方向的费米速度，定义手性C=sgn[detνij]。 为了简便我们取各向同性的情况，即H=Cħνk·σ。前一节，我们得到了外尔费米子波包在界面散射会产生横向位移（IF位移），因此我们期待波包受杂质散射也存在横向位移。虽然散射也可能会导致纵向位移，但是纵向位移不提供角动量，不会产生明显的物理效应。由于体系具有z轴的旋转对称性，因此可以考虑杂质散射过程中z方向的角动量守恒，从而得到手性保护位移。由于外尔费米子无质量，其手性和螺旋度是一致的，而螺旋度是自旋角动量在正则动量方向的投影。手性C=±1分别对应自旋与动量平行与反平行的情况。受到杂质散射前后，自旋角动量改变量为其中r表示波包出射方向的单位矢量 (sinθcosϕ,sinθsinϕ,cosθ)，此式表示最初沿着z方向的自旋，散射后沿着散射方向，他们之间的差值就是自旋改变量。对应的轨道角动量该变量为 ∆L=δch×pout，其中δch= ∆ch(sinθ0cosϕ0,sinθ0sinϕ0,cosθ0) 是散射过程中的横向位移，pout=pr是散射波包的正则动量。我们考虑正入射，经过散射后，波包处于x-y平面内如图 25(c)(d)所示。 散射后手性位移矢量满足θ0=π/2,ϕ0=ϕ±π/2。考虑z方向角动量守恒，即得到手性保护位移大小：

进而得到横向位移矢量：

对于手性C=±1的外尔费米子，图 25(b)是不同散射角度下，手性保护位移与费米能的关系，可以看到随着θ增大，∆ch剧烈增加。

C.半经典分析

在波包散射过程中，我们定义碰撞因子b，其物理意义是波包中心到散射中心的垂直距离（见图25(a)）。按照波包散射理论，波包对散射截面贡献的几率P(θ,b)，会随着b的增加而呈指数衰减[148]：

其中 ∆r表示波包展宽，σ(θ)是平面波散射截面。而由于手性保护位移的存在使得：

图26. (a)量子弛豫时间（红色实线）和输运弛豫时间（蓝色实线）随着费米能的变化关系。其中 (b) 波包散射（蓝色实线）和平面波散射（红色虚线）对应的弛豫时间比值Rτ和Rτ0。图片来自文献 [146]。

从而将P(θ,b)修正为：

背散情况下θ=π，∆ch→∞P(θ,b)→0，这表明背散被手性保护位移完全压制。同时当θ比较大时，由于∆ch对的修正也很大，造成P(θ,b)随着θ的增大呈指数衰减。这也就意味着，外尔半金属中的大角度散射也被压制，只有小角度散射才是可能的。小角度散射是二维电子气超高迁移率的物理原因，但这里导致这一现象的物理机制是完全不同的，二维电子气大角度散射被压制来源于载流子与杂质在空间分离，而在外尔半金属体系，这一现象来自于手性保护位移∆ch。为了更深入的理解以上结果，我们采用量子力学中处理散射问题的一般方法来作进一步验证。

D.波包散射

体系哈密顿量为：

其中V(r)为无序或缺陷，在玻恩近似下，散射波满足：

图27.实验测量的弛豫时间比值，图中分立的点取值于实验数据，蓝色实线是我们理论预测。图片来自文献[150]

其中G(r−r′)为不考虑无序与缺陷时的格林函数，它满足的演化方程：

其中H0=ħνk·σ。 与之前构造波包的方法类似，我们得到入射波包：

其中是波包展宽,根据格林函数与入射波包，可得到散射波包：

进而散射波包散射几率为：

经过一系列的计算后，得到波包对散射截面贡献的几率：

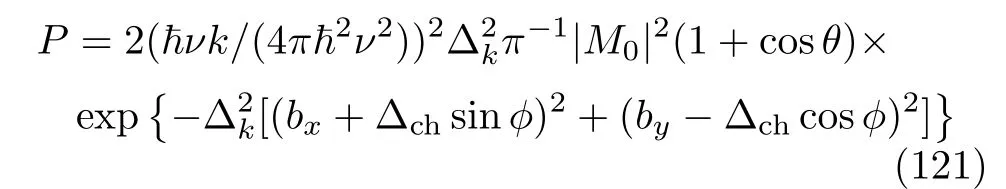
∆ch=不难发现采用量子力学方法也得到了与半经典方法相同的指数修正项，再次验证了手性保护位移修正碰撞因子大小，进而导致了大角度下波包散射概率的急剧减小。

为了计算量子弛豫时间与输运弛豫时间，我们将碰撞因子积掉，碰撞因子的截断bc取决于杂质浓度。根据Eq.(105)和Eq.(106)可以得到弛豫时间如图26(a)所示。杂质浓度取为1018cm−3,bc=5 nm大约是最近邻杂质距离的一半。两个弛豫时间都会在高费米能位置达到饱和。而图26(b)显示，Rτ随着费米能接近Weyl点而陡增。弛豫时间比很大意味着体系具有很高的迁移率，这就是外尔半金属中超高电子迁移率的机制。这一机制已经被实验验证，如图27所示，北京大学贾爽研究组在TaAs样品分别测定了输运弛豫时间和量子弛豫时间，在费米能级靠近外尔点时，弛豫时间比值Rτ突然增大。

VI.总结

随着物理学家的努力，拓扑概念结合凝聚态材料展现给我们越来越丰富的物理特性。继拓扑绝缘体之后，外尔半金属作为一种全新的拓扑半金属态拥有非常新奇的物性和丰富的输运现象。我们着重介绍了外尔半金属体系一些基本的概念如手性反常、手性磁效应、贝里曲率、手性朗道能级等一系列与输运相关的物性。我们相信对外尔半金属的深入研究能够帮助我们更好的揭示拓扑这一数学概念在凝聚态研究中所起的作用。

在这篇综述中，也着重介绍了过去几年我们在外尔半金属输运领域的工作。我们介绍了无序对两类外尔半金属的影响并分别获得了第一类以及第二类外尔半金属在无序下的完整相图。与自洽玻恩近似的结果相比较，弱无序下的外尔点仍然是稳定的，此外我们发现第二类外尔半金属的输运性质比第一类外尔半金属更优越。我们研究了无序类型对外尔半金属磁阻的影响，分别考虑了两种特定的无序：长程无序以及短程无序。我们发现对于长程无序高朗道能级辅助的背散变的很重要，这种情况下玻尔兹曼方程不再适用。我们研究了外尔半金属中类光学输运，在此基础上得到了外尔半金属的GH和IF位移，我们发现IF位移是一种手性保护的拓扑位移，它完全取决于外尔半金属的拓扑特性，基于这些特性，我们提出IF位移能够在判断费米弧、构造谷量子器件、测定贝利曲率方面具有巨大的应用前景。最后我们利用手性保护拓扑位移提出了拓扑半金属中的超高电子迁移率问题的一种可能解释。

致 谢

感谢一直以来谢心澄、孙庆丰在本综述所总结工作中的指导与合作，感谢与汪自强、刘海文、宋俊涛、吴宜家的合作以及他们在本综述中的贡献。感谢与王乾君、潘义明、贾爽、卢海舟、修发贤、唐维等的深入讨论。感谢国家自然科学基金11534001、国家重点基础研究发展计划2014CB920901以及江苏省自然科学基金杰出青年项目BK20160007的资助。

[1]Klitzing K Von,Dorda G,Pepper M.Phys.Rev.Lett.,1980,45:494

[2]Wen X G.Phys.Rev.B.,2002,65:165113

[3]Thouless D J,Kohmoto M,Nightingale M P,et al.Phys.Rev.Lett.,1982,49:405

[4]Haldane F D M.Phys.Rev.Lett.,1988,61,2015

[5]Liu C C,Jiang H,Yao Y.Physical Review B,2011,84:195430

[6]Kane C L,Mele E J.Phys.Rev.Lett.,2005,95:226801

[7]Qi X L,Zhang S C.Rev.Mod.Phys.,2011,83:1057

[8]Hasan M Z,Kane C L.Rev.Mod.Phys.,2010,82:3045

[9]Novoselov K S,Geim A K,Morozov S V,et al.Science,2004,306:666

[10]Novoselov K S,Geim A K,Morozov S V,et al.Nature,2005,438,197

[11]Pal P B.American Journal of Physics,2011,79:485

[12]Xu Y,et al.Science.,2015,349:613

[13]He Q L,et al.Science.,2017,357:294

[14]Wan X G,Turner A M,Vishwanath A,et al.Phys.Rev.B,2011,83,205101

[15]Weng H,Fang C,Fang Z,et al.Phys.Rev.X,2015,5:011029

[16]Lv B Q,Weng H M,Fu B B,et al.Phys.Rev.X,2015,5:031013

[17]Xu S Y,et al.Science,2015,349:613-617

[18]Zyuzin A A,Wu S,Burkov A A.Phys.Rev.B,2012,85:165110

[19]Yang K Y,Lu Y M,Ran Y.Phys.Rev.B,2011,84:075129

[20]Soluyanov A A,Gresch D,Wang Z J,et al.Nature,2015,527:495

[21]Ke D,Wan G L,Deng P,et al.Nature Physics,2016,12:1105

[22]Hosur P,Qi X L,C.R.Physique,2013,14:857

[23]Burkov A.Science,2015,350:378

[24]Jun X,et al.Science,2015,350:413

[25]Lu H Z,Shen S Q.Frontiers of Physics,2017,12:127201

[26]Li Y P,et al.Frontiers of Physics,2017,12:127205

[27]Xiao Y,Zhang C,Liu S S,et al.Frontiers of Physics,2017,12:127209

[28]Hasan M Z,Xu S Y,Belopolski I,et al.Annual Review of Condensed Matter Physics,2017,8:289-309

[29]Xu S Y,et al.Science,2015,347:294

[30]Zhang C L,et al.Nature Physics,2017,13:979

[31]Jiang H,Cheng S G,Sun Q F,et al.Phys.Rev.Lett.,2009,103:036803

[32]Hua J,et al.Phys.Rev.B,2009,80:165316

[33]Jian L,et al.Phys.Rev.Lett.,2009,13:136806

[34]Groth C W,Wimmer M,Akhmerov A R,et al.Phys.Rev.Lett.,2009,103,196805

[35]Wu B L,Song J T,Zhou J J,Jiang H.Chinese Physics B.,2016,11:009

[36]Chen C Z,Liu H W,Jiang H,et al.Phys.Rev.B,2016,93:165420

[37]Chen C Z,Song J,Jiang H,et al.Phys.Rev.Lett.,2015,115:246603

[38]Liu S,Ohtsuki T,Shindou R.Phys.Rev.Lett.,2016,116:066401

[39]Wu Y J,Liu H W,Jiang H,et al.Phys.Rev.B,2017,96:024201

[40]Jiang Q D,Jiang H,Liu H,et al.Phys.Rev.Lett.,2015,115:156602

[41]Yang S A,Pan H,Zhang F.Phys.Rev.Lett.,2015,115:156603

[42]Yu R,Fang Z,Dai X,et al.Frontiers of Physics.,2017,12:127202

[43]Pan X C,et al.Frontiers of Physics,2017,12:127203

[44]Hong L,Jia S.Frontiers of Physics,2017,12:127211

[45]Chiu C K,Teo J C Y,Schnyder A P,et al.Reviews of Modern Physics,2016,88:035005

[46]Weng H,Dai X,Fang Z J.Phys.:Condens.Matter,2016,28:303001

[47]Vafek O,Vishwanath A.Annu.Rev.Condens.Matter Phys.,2014,5:83

[48]Burkov A A,Metals W.Annu.Rev.Condens.Matter Phys.,2018,9:359

[49]Hosur P,Qi X.Comptes Rendus Physique,2013,14:857

[50]Jia S,Xu S Y,Hasan M Z.Nature Materials,2016,15:1140

[51]喀兴林，高等量子力学，第二版，高等教育出版社。

[52]Srednicki M,Quantum Field Theory

[53]Nielsen H B,Ninomiya M.Phys.Lett.,1983,130B:389

[54]Zhou J H,Jiang H,Niu Q,et al.Chin.Phys.Lett.,2013,30:027101

[55]Goswami P,Tewari S.Phys.Rev.B,2013,88:245107

[56]Fujikawa K.Physical Review D,1980,21:2848

[57]Andreev A V,Spivak B Z.Phys.Rev.Lett.,120:026601

[58]David B.Chiral Symmetry and Lattice Fermions:arXiv:0912.2560

[59]Nielsen H B,Ninomiya M.Nuclear Physics B,1981,185,20

[60]Nielsen H B,Ninomiya M.Nuclear Physics B,1981,193:173

[61]Vazifeh M M,Franz M.Phys.Rev.Lett.,2013,111:027201

[62]潘义明，Weyl半金属手征输运研究，Phd thesis,南京大学2016

[63]Son D T,Spivak B Z.Phys.Rev.B,2013 88:104412

[64]Li C Z,Wang L X,Liu H,et al.Nature communications,2015,6:10137

[65]Wang Y,Liu E,Liu H,et al.Bulletin of the American Physical Society.,2017,13:62

[66]Arnold F,Shekhar C,Wu S C,et al.Nature communications,2016,17:7

[67]Zhang C L,Xu S Y,Belopolski I,et al.Nature communications,2016,7:10735

[68]Zhang C,Zhang E,Wang W,et al.,2017,8:13741

[69]Son D T,Spivak B Z.Phys.Rev.B,2013,88:104412

[70]Li C Z,Wang L X,Liu H,et al.Nature communica-tions,2015,6:10137

[71]Wang Y,Liu E,Liu H,et al.Bulletin of the American Physical Society,2017,62:13142

[72]Arnold F,Shekhar C,Wu S C,et al.Nature communications,2016,17:7

[73]Zhang C L,Xu S Y,Belopolski I,et al.Nature communications,2016,7:10735

[74]Zhang C,Zhang E,Wang W,et al.Nature communications,2017,8:13741

[75]Andreev A V,Spivak B Z.Phys.Rev.Lett.,120:026601

[76]梁灿彬，周彬，微分几何入门与广义相对论（上册），第二版，科学出版社。

[77]Xiao D,Chang M C,Niu Q.Reviews of Modern Physics,2010,82,1959

[78]Nakahara M,Geometry,Topology and Physics:2rd ed,IOP2003)

[79]Lu H Z,Zhang S B,Shen S Q.Phys.Rev.B,2015,92:045203

[80]Bernevig B A,Hughes T L,Zhang S C.Science,2006,314:1757-1761

[81]Jiang H,Qiao Z,Liu H,et al.Phys.Rev.B,2012,85:045445

[82]Li J,Chu R L,Jain J K,et al.Phys.Rev.Lett.,2009,102:136806

[83]Rycerz A,Tworzydlo J,Beenakker C W J.Europhys.Lett.,2007,79:57003

[84]C H Lewenkopf,Mucciolo E R,Castro Neto A H.Phys.Rev.B,2008,77:081410

[85]Zhang Y Y,Hu J P,Bernevig B A,et al.Phys.Rev.Lett.,2009,102:106401

[86]Zhang Y Y,Hu J P,Bernevig B A,et al.Phys.Rev.Lett.,2009,102:106401

[87]Braun D,Hofstetter E,MacKinnon A,et al.Phys.Rev.B,1997,55:7557

[88]Slevin K,Markos P,Ohtsuki T.Phys.Rev.Lett.,2001,86:3594

[89]Datta S,Electronic Transport in Mesoscopic systems:世界图书出版社2004

[90]Lee D H,Joannopoulos J D.Phys.Rev.B,1980,23:4997

[91]Lopez Sancho M P,Lopez Sancho J M,Sancho J M L,et al.J.Phys.F:Met.Phys.,1985,15:851

[92]Weiβe A,Wellein G,Alvermann A,et al.Rev.Mod.Phys.,2006,78:275

[93]Mahan G D,Many-Particle Physics:3rd ed.Plenum,NewYork,2000

[94]Lu H Z,Zhang S B,Shen S Q.Phys.Rev.B,2015,92:045203

[95]Zhang S B,Lu H Z,Shen S Q.New J.Phys.,2016,18:053039

[96]Das Sarma S,Xie X C.Phys.Rev.Lett.,1988,61:738

[97]Xie X C,Li Q P,Das Sarma S.Phys.Rev.B,1990,42:7132

[98]Hosur P,Parameswaran S A,Vishwanath A.Phys.Rev.Lett.,2012,108:046602

[99]Ominato Y,Koshino M.Phys.Rev.B,2014,89:054202

[100]Biswas R R,Ryu S.Phys.Rev.B,2014,89:014205

[101]Sbierski B,Pohl G,Bergholtz E J,et al.Phys.Rev.Lett.,2014,113:026602

[102]Sbierski B,Bergholtz E J,Brouwer P W.Phys.Rev.B,2015,92:115145

[103]Fradkin E.Phys.Rev.B,1986,33:3263

[104]Kobayashi K,Ohtsuki T,Imura K I,et al.Phys.Rev.Lett.,2014,112:016402

[105]Prodan E.J.Phys.A,2011,44:113001

[106]Prodan E.Appl.Math.Res.Express,2013,2013:176

[107]Goswami P,Pixley J H,Das Sarma S.Phys.Rev.B,2015,92:075205

[108]Burkov A A,Balents L.Phys.Rev.Lett.,2011,107:127205

[109]Qi X L,Wu Y S,Zhang S C.Phys.Rev.B,2006,74:085308

[110]MacKinnon A,Kramer B.Phys.Rev.Lett.,1981,47:1546

[111]MacKinnon A,Kramer B.Z.Phys.B,1983,53:1

[112]Kramer B,MacKinnon A.Rep.Prog.Phys.,1993,56:1469

[113]Chalker J T,Dohmen A.Phys.Rev.Lett.,1995,75:4496

[114]Wang Z.Phys.Rev.Lett.,1997,79:4002

[115]Kobayashi K,Ohtsuki T,Imura K I.Phys.Rev.Lett.,2013,110:236803

[116]Xu Y Y,Zhang F,Zhang C.Phys.Rev.Lett.,2015,115:265304

[117]Xu G,Weng H M,Wang Z J,Dai X,et al.Phys.Rev.Lett.,2011,107:186806

[118]Huang L,McCormick T M,Ochi M,et al.Nature Materials,2016,15:1155

[119]Wang C L,Zhang Y,Huang J W,et al.arXiv preprint arXiv:1604.04218

[120]Xu N,Wang Z J,Weber A P,et al.arXiv preprint arXiv:1604.02116,2016

[121]Koepernik K,Kasinathan D,Efremov D V,et al.Phys.Rev.B,2016,93,201101

[122]Yan M Z,Huang H Q,Zhang K N,et al.arXiv preprint arXiv:1607.03643

[123]O’Brien T E,Diez M,Beenakker C W J.Phys.Rev.Lett.,2016,116:236401

[124]Park M J,Basa B,Gilbert M J.Phys.Rev.B,2017,95:094201

[125]Li F Y,Luo X,Dai X,et al.Phys.Rev.B,2016,94:121105

[126]Su Y,Wang X S,Wang X R.ArXiv:1701.00905

[127]Liang T,Gibson Q,Ali M N,et al.Nature materials,2015,14:280

[128]Goos F,H¨anchen H.Annalen der Physik,1947,436:333

[129]Huang J H,Duan Z L,Ling H Y,et al.Phys.Rev.A,2008,77:063608

[130]de Haan V O,Plomp J,Rekveldt T M,et al.Phys.Rev.Lett.,2010,104:010401

[131]Fradkin D M,Kashuba R J.Phys.Rev.D,1974,9:2775

[132]Fedorov F I.DOKLADY AKADEMII NAUK SSSR,1955,105:465–468

[133]Beenakker C W J,Sepkhanov R A,Akhmerov A R,et al.Phys.Rev Lett,2009,102:146804

[134]Imbert C.Phys.Rev.D,1972,5:787

[135]Schilling H,der Physik A,1965,471:122–134

[136]Player M A.Journal of Physics A:Mathematical and General,1987,20:3667

[137]Liberman V S,Zel’dovich B Ya.Phys.Rev.A,1992,46:5199

[138]Onoda M,Murakami S,Nagaosa N.Phys.Rev.Lett.,2004,93:083901

[139]Bliokh K Y,Bliokh Y P.Phys.Rev.Lett.,2006,96:073903

[140]Hosten O,Kwiat P.Science,2008,319:787

[141]蒋庆东，拓扑半金属中的波包散射，phd thesis,北京大学2017)

[142]Liu Y,Yu Z M,Yang S A.Phys.Rev.B,2017,96:121101

[143]Yang S Y A,Pan H,Zhang F.Phys.Rev.Lett.,2015,115:156603

[144]Wang L Y,Jian S K,Yao H.Phys.Rev.A,2016,93:061801

[145]Wang L Y,Jian S K.Phys.Rev.B,2017,96:115448

[146]Jiang Q D,Jiang H,Liu H,et al.Phys.Rev.B,2016,93,195165

[147]Liang T,Gibson Q,Ali M N,et al.Nature Materials,2014,14:280

[148]Ron C.Some notes on steganography:Posted on steganography mailing list 1998):1-6

[149]Tafti F F,Gibson Q D,Kushwaha S K,et al.Nature Physics,2016,12:272

[150]Zhang C L,Yuan Z J,Jiang Q D,et al.Phys.Rev.B,2017,95:085202.