平面概念与公理的历史发展*

沈中宇　汪晓勤

(1.华东师范大学数学系　200241; 2.华东师范大学教师教育学院　200062)

平面概念与公理是高中立体几何的起始内容，是联结平面几何与立体几何的纽带，也是学生学习后续立体几何知识的基础.现行人教版和沪教版高中数学教科书都是从现实情境出发，抽象出平面概念，然后基于生活经验给出三个公理，其中人教版给出的三个公理如下：

公理1如果一条直线上的两点在一个平面内，那么这条直线在此平面内；

公理2过不在一条直线上的三点，有且只有一个平面；

公理3如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.

为何将平面作为不加定义的原始概念？平面的三个公理从何而来？公理与公理之间有何联系？对于这些问题，教科书没有作出任何交待.从历史上看，自希尔伯特(D. Hilbert, 1862-1943)将点、线、面视为几何公理体系中不加定义的原始概念之后，人们在接受希尔伯特公理体系的同时，也往往误将点、线、面视为易于理解的简单概念.然而，教学实践表明，平面概念以及相关公理因为其抽象性而成了学生的学习难点.

有关研究表明，学生对平面的理解具有历史相似性[1].那么，如何在教学中让学生更好地理解平面概念的本质以及相关公理，从而顺利跨越他们的认知障碍？我们希望从HPM视角来实施教学，以实现上述目的.为此，我们需要从前人的教科书中汲取思想的养料.另一方面，由于在高中数学教科书开始修订之际，我们也需要对西方早期教科书进行研究，以便获取有用的素材.

本文就平面概念这一主题，对几何原本、历史上数学家的论述以及20世纪中叶之前的西方立体几何教科书进行考察，试图勾勒出平面概念与公理的历史发展脉络，为教学和教科书编写提供参考.

1　古希腊时期的平面定义

早在公元前5世纪，古希腊哲学家巴门尼德(Parmenides)对平面概念已作过刻画.根据普罗克拉斯(Proclus, 412-485)的记载[1]，巴门尼德将几何对象(一维、二维和三维)分成“直的”、“曲的”和“混合的”三类.如果一个二维对象是直的表面，那么它就是一个平面，直线可在任意方向与之相合.这里，巴门尼德将“直”作为平面的本质特征.

欧几里得(Euclid, 前3世纪)并未沿用巴门尼德的定义，他将平面定义为“与其上直线一样平放着的面”[2]，该定义中出现了若干模糊的词语，如“一样”、“平放”.关于平面，《几何原本》卷11给出了三个命题.

命题1一条直线不可能一部分在平面内，而另一部分在平面外.

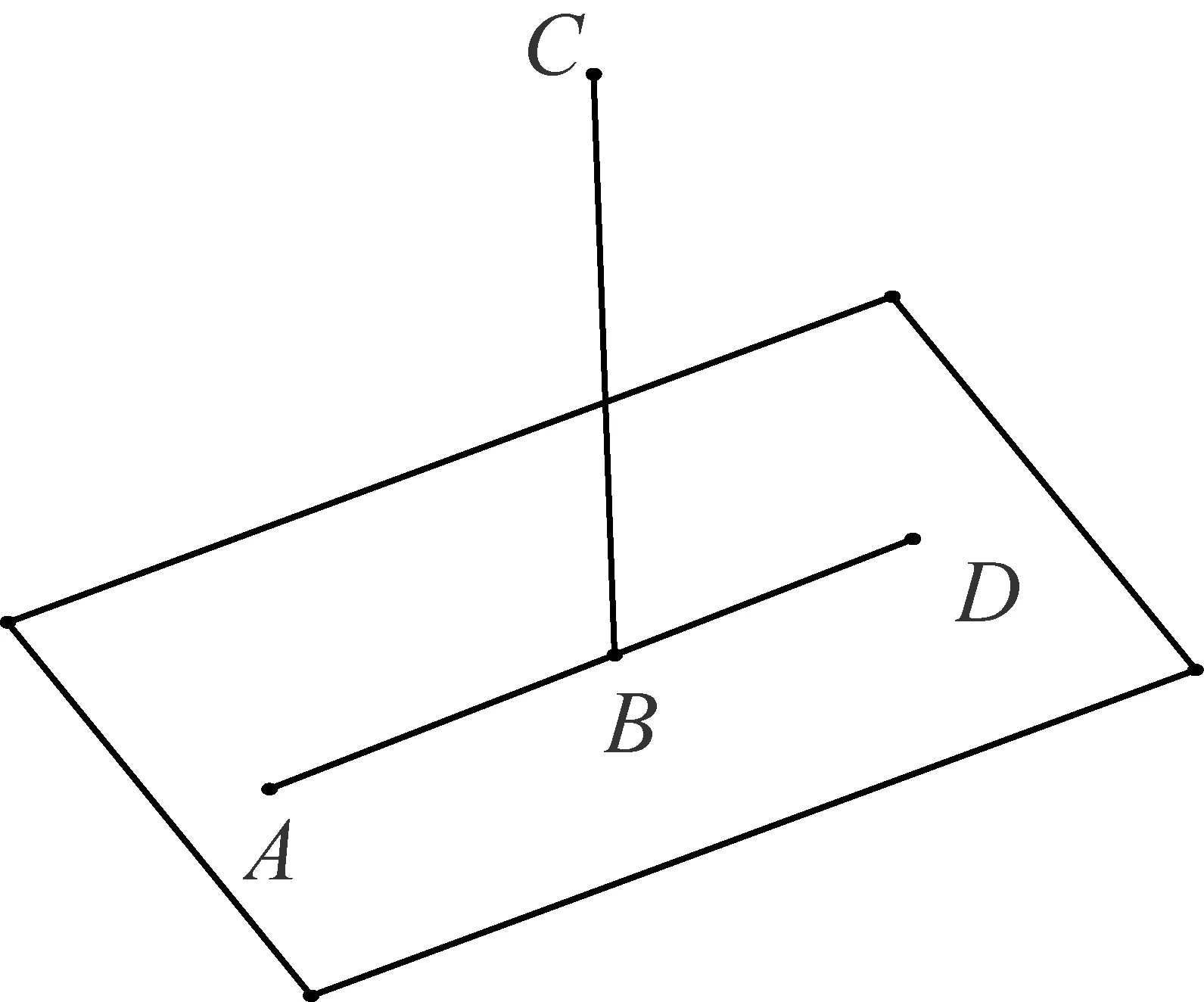
图1

如图1，设直线ABC的一部分AB在一个平面上，而另一部分BC在该平面外，则在该平面上就有一条直线BD与AB在同一直线上.于是，AB是两条直线ABC，ABD的公共部分，这是不可能的，假设不成立，命题得证.

命题2若两条直线彼此相交，则它们在同一平面内；它们构成的三角形也都位于同一平面内.

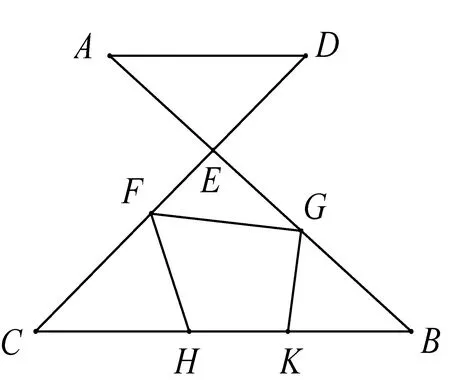
图2

如图2，设直线AB和CD交于点E，在EC和EB上分别取点F，G.联结CB，FG；引FH，GK.首先证明△ECB在同一平面上，假设它的一部分FHC或GBK在一个平面内，而余下部分在另一平面内，则直线EC或EB的一部分在一个平面内，余下部分在另一平面内.这是不可能的.同样可证其余部分也都在一个平面内，故△ECB在一个平面内.但△ECB所在平面也是EC和EB所在平面，又EC和EB所在平面也是AB和CD所在平面，命题得证.

命题3若两平面相交，则它们的交线是一条直线.

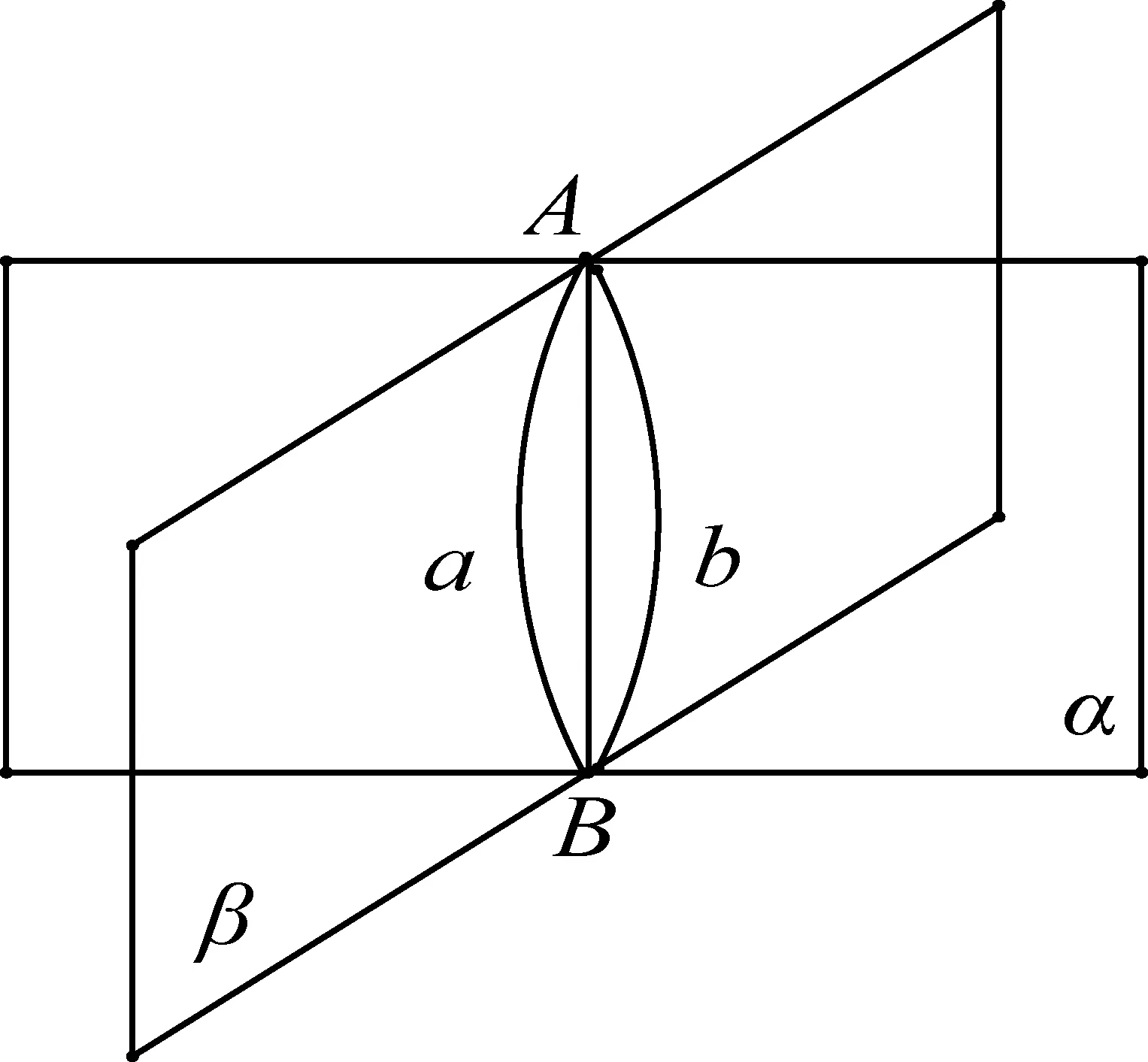
图3

如图3，设平面α和β相交，AB是其交线.若AB不是直线，设A和B在平面α上的连线为a，在平面β上的连线为b.因直线a和b有相同端点，它们围成一个面片，这是不可能的，故假设不成立，命题得证.

可见，今日人教版教科书中的平面三公理最初是在《几何原本》中以命题形式出现的，其中命题1的形式与人教版中的公理1有较大的不同，不是取直线上两点，而是直线的一部分.欧几里得的定义存在一定的问题，首先，平面需要一个更加清晰的定义.其次，平面的存在性需要通过构造被保证.而且在证明上述三个命题时，并未用到平面的定义.针对欧几里得平面定义的问题，随后的数学家和评论者尝试给出平面更为清晰的定义，首先值得注意的是古希腊数学家海伦(Heron, 约公元1世纪)，他给出了平面的新定义：“平面是具有以下性质的面，它向四周无限延伸，平面上的直线都与之相合，且若一条直线上有两点与之相合，则整条直线在任意位置与之相合.”[1]，这实际上就是人教版中的公理1.

我们可以看到此阶段对平面的定义都关注平面“直”的特征并试图去刻画它.

2　构造性定义阶段

17世纪，德国数学家莱布尼兹(G. W. Leibniz, 1646～1710)做了很多尝试消除欧几里得逻辑上的不完美，他也批评海伦的定义，因为他觉得这一定义是“重复判断的”，也就是说，这一定义包含过多的需要描述平面的事物.因此他给出了一个更简单的定义：“平面是一组这样的点，它们到两定点的距离相等”[1].显然的，莱布尼兹在空间中考虑几何对象并定义它们，同时，他实质上也给出了一个平面的构造.

18世纪，英国数学家辛松(R. Simson,1687～1768)给出了平面的新定义：“平面是具有下列性质的面，通过其上任意两点的直线完全包含在该面上.” 辛松的定义实际上与海伦的定义等价，被称为“辛松定义”[1].

法国数学家傅里叶(B. J. Fourier, 1768～1830)给出了平面的下列构造性定义：“平面由经过直线上一点且与直线垂直的所有直线构成”[2]，傅里叶定义的优势在于通过这一定义，利用全等三角形可以推出辛松定义中的平面的性质.但傅里叶的定义采用了“垂直”这一概念，“垂直”先于平面给出，受到人们的质疑.

19世纪，德国数学家克雷尔(A. L. Crelle, 1780～1855)认为，一个好的定义必须简洁且可用于推理，因此，一个合适的定义是很难找的.在以上这些定义中，不管是简单的还是复杂的，都包含了一些多余的假定.以辛松的定义为例，如图4，假设一个平面上有三角形ABC，D和E是BC和AC上任意两点，连接AD和BE，根据辛松的定义，AD和BE都在平面上，则AD和BE必定相交于点F，不然在问题中就存在两个平面，而不是一个，但实际上，没有任何证据说明AD和BE一定相交.克雷尔给出平面的另一个定义：“平面是包含所有通过空间中一个定点并与另一条直线垂直的直线的面”.克雷尔的定义也有类似问题，他自己也承认从这一定义推不出一些必要的性质[2].

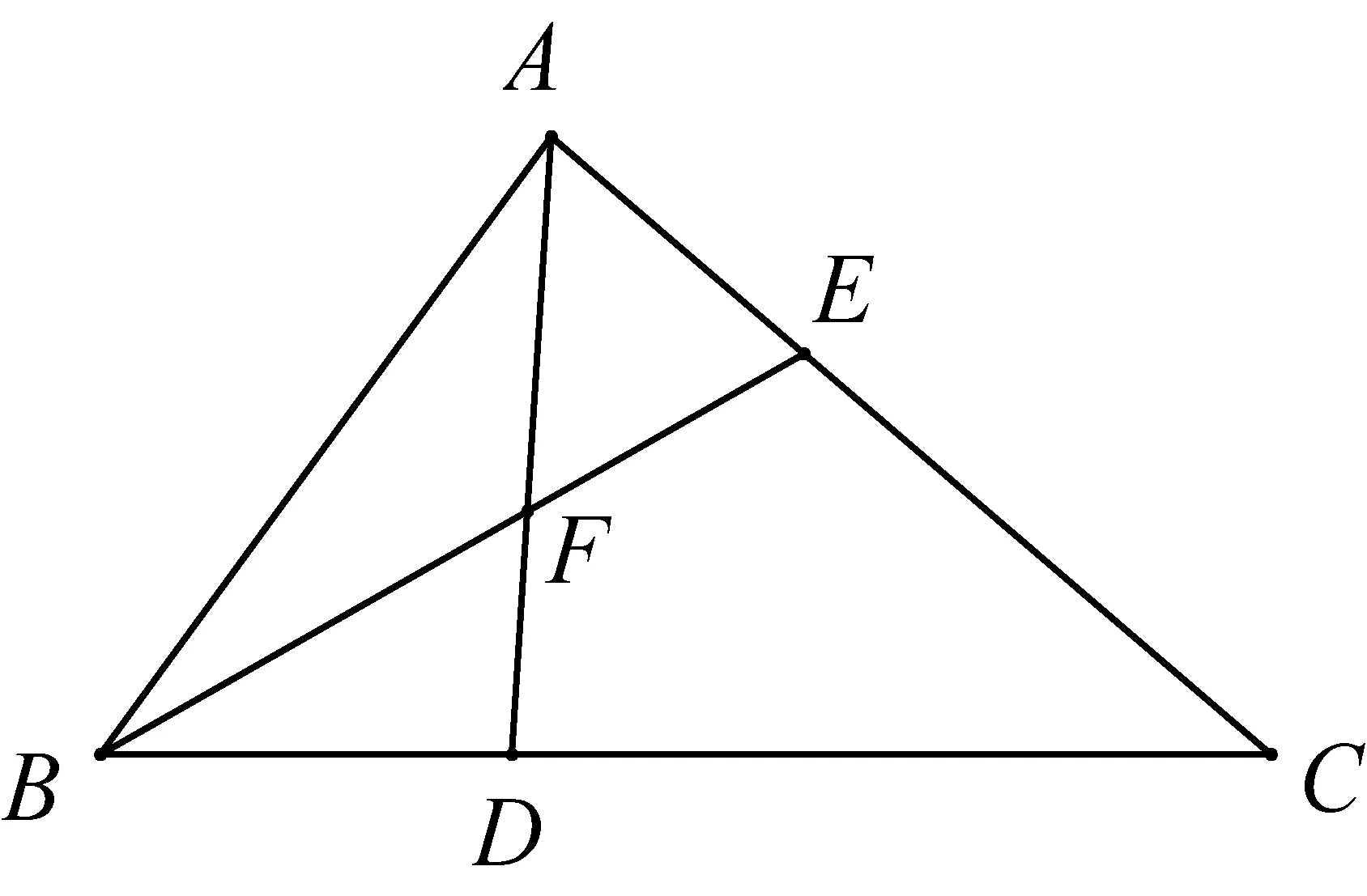
图4

德国数学家迪纳(F. Deahna, 1815～1844)给出平面的另一种构造方法：“将一个球绕着它的直径旋转，球面上所有的点旋转成一条封闭的曲线，即圆，其中一条将球面分成全等的两半，连接球心与圆的直线形成平面”[2]，这一定义避免使用了“垂直”这一概念，Becker在此基础上提出直角的一条边绕着另一条边旋转也可形成平面.

著名数学家如高斯(C. F. Gauss, 1777～1855)、W·波尔约(W. Bolyai, 1775～1856)及其子J·波尔约(J. Bolyai, 1802～1860)、罗巴切夫斯基(N. I. Lobachevsky, 1792-1856)也相继给出了平面的构造性定义.高斯认为辛松的定义被称为定义来说太强了，他认为这应该被一个更弱的定义替代，然后再证明辛松的性质.高斯将平面定义为“过一个定点，且垂直于一条直线的所有直线构成的面”，W·波尔约将平面定义为“一条直线绕着另一条与之垂直的直线旋转而成的面”[2],J·波尔约利用对称来构造平面.如图5，已知不共线三点A，B和C，点D分别绕AB、AC和BC旋转，所形成的三个圆相交于点E，该点是点D关于点A，B和C所确定平面的对称点，J·波尔约将平面定义为点D和点E重合的那些点.罗巴切夫斯基构造平面如下：“以空间中两点为球心，半径相同且不断增长，则两个球的交线(即圆)形成平面.”[1]

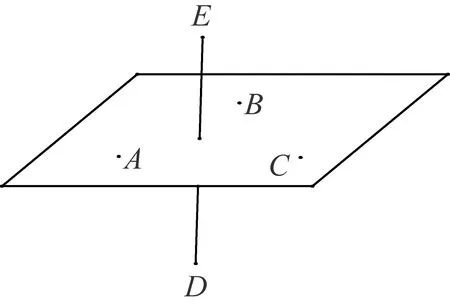
图5

因此，在此阶段，针对欧几里得与海伦定义的不足，数学家给出了很多构造性定义，这些定义大致可以将其分成两类：一类是莱布尼兹的传统，利用对称来构造平面，一类是傅里叶的传统，利用相互垂直的直线平移或旋转来构造平面.

3　包含式定义阶段

虽然出现了一些构造性定义，辛松的定义还是为18-19世纪的绝大多数几何教科书所采用，由于其中突出了直线包含在平面内的特征，我们称之为“包含式定义”.在此阶段，人教版的公理1被用作平面的定义，其余两个公理皆以定理的形式由此定义推出，因此，平面的定义开始真正用于平面有关性质的证明.接下来，我们对此阶段几何教科书中的平面定义与有关命题进行考察.

3.1　1800—1850：平面定义开始应用于相关定理

从这一时期开始，平面的定义被真正用于相关命题的证明.18世纪法国数学家勒让德(A. M. Legendre, 1752～1833)在其《几何与三角学基础》(1800)[3]中将平面定义为：“一个面，如果其上两点的连线全部在面上，则称其为平面”，与辛松的定义相同.利用该定义，勒让德证明了欧几里得的三个定理.

定理1一条直线不能部分在平面上，而部分不在上面.

根据平面的定义，当一条直线有两个点在平面上时，它全部在平面上，因此命题成立.同时说明了，想要检验一个面是否为平面，可以将一条直线用不同方式与面相合，观察其是否完全与面相合.

定理2两条相交直线位于同一平面上，且确定它的位置.

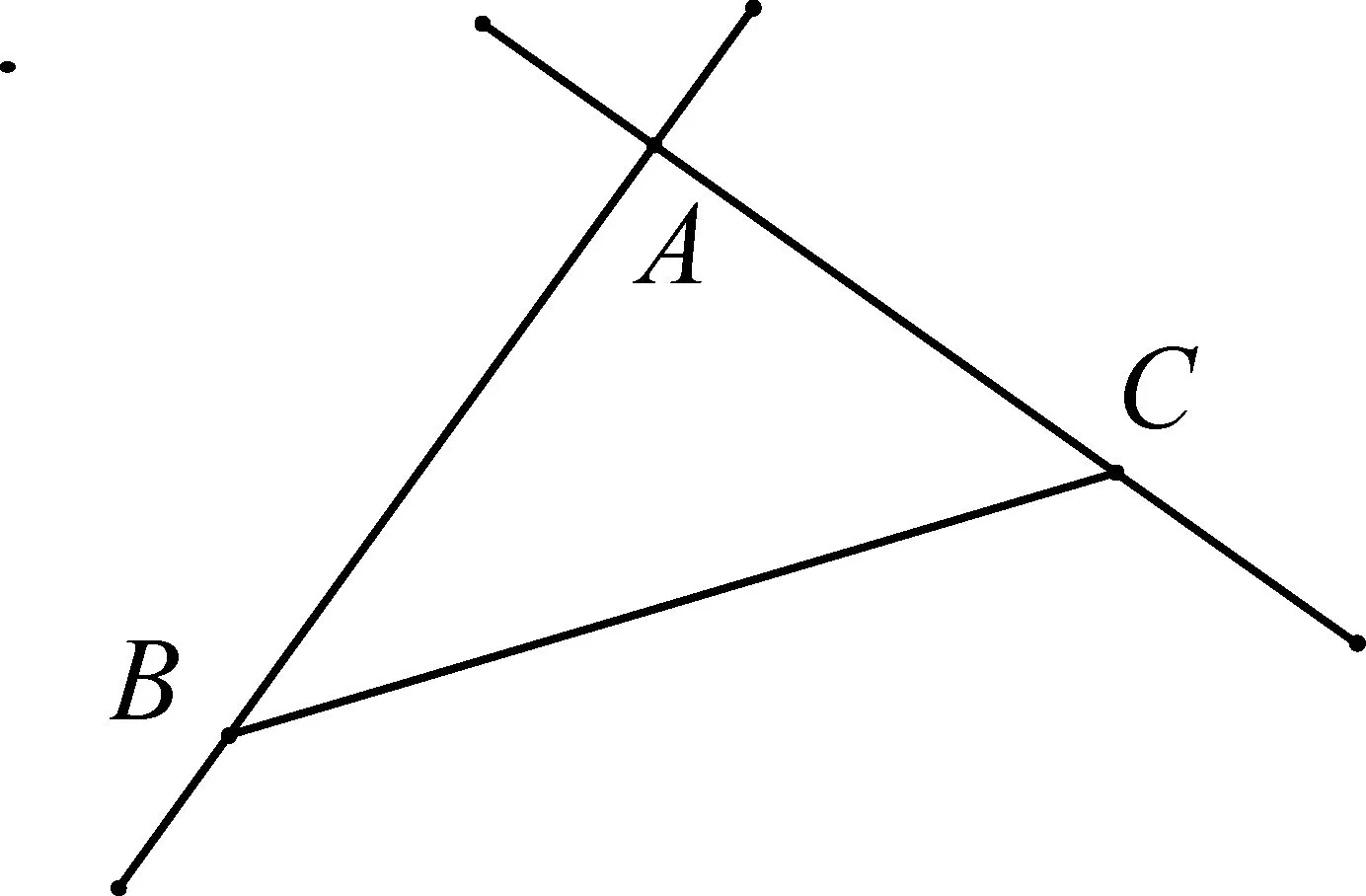
图6

如图6所示，两直线AB和AC交于点A，与AB相合的平面绕AB旋转，直到通过点C，根据定义，AC全部在平面上.因此，平面位置由直线AB和AC所确定.勒让德给出定理2的两个推论：

推论1不共线的三点确定一个平面.

推论2两条平行直线确定一个平面.

定理3如果两个平面相交，则它们的交线是直线.

假设有除直线之外的点同时在两个平面上，则有三个点不在同一直线上，根据定理2推论1，三点确定一个平面，所以假设不成立.

在定理3的证明中，勒让德没有说明为什么两个平面的交线为直线，因此存在缺陷，苏格兰数学家普雷菲尔(J. Playfair, 1748-1819)在《几何学基础》(1829)[4]中说明，设有两点为它们的公共点，根据平面定义，这两点的连线也是公共的，从而让证明变得更加完整，后世的很多教科书中都采用了此种方法.

以上可见，定理1可以直接用定义来证明，定理2先用旋转的方式，然后又用到了平面的定义，定理3先用了定理2再用了平面的定义.Hayward在《几何学基础》(1829)[5]中先证明定理3，再证明定理2，此种顺序导致定理3的证明只能说明交线有一条直线，但未能说明为什么直线之外没有其他公共部分.但也有教科书虽然沿用勒让德的顺序，但也缺少了交线之外没有其他公共部分的证明，如Davies的《几何学基础》(1841)[6].有些教科书对这一模式进行一定的微调，Peirce在其《平面与立体几何基础》(1837)[7]中直接证明“不共线三点确定一个平面”，而不是将其作为定理2的推论.很多教科书并未将定理1作为单独的定理列出，如Walker的《几何学基础》(1829)[8]，这也成为后世教科书的普遍做法.

3.2　1850—1880：定理2的证明的不断改进

勒让德利用旋转来确保定理2中的平面的唯一性，显得不够严谨.因此，这一时期的一些教科书开始采用不同的方式来解决该问题.

Tappan在其《平面与立体几何》(1864)[9]中用传统几何的方式来证明平面的唯一性.如图7，假设不共线三点A，B，C在两个平面α和β上，根据平面的定义，AB，AC和BC都在平面α和β上.在平面α上任取一点D，过D作直线交AC于E，因D和E都在平面α上，故直线ED在平面α上，从而必与AB或BC相交.不妨设ED与AB交于点F，因F和E都在平面β上，故直线FD也在平面β上，从而点D也在平面β上.因此，三点A，B，C确定唯一的平面.

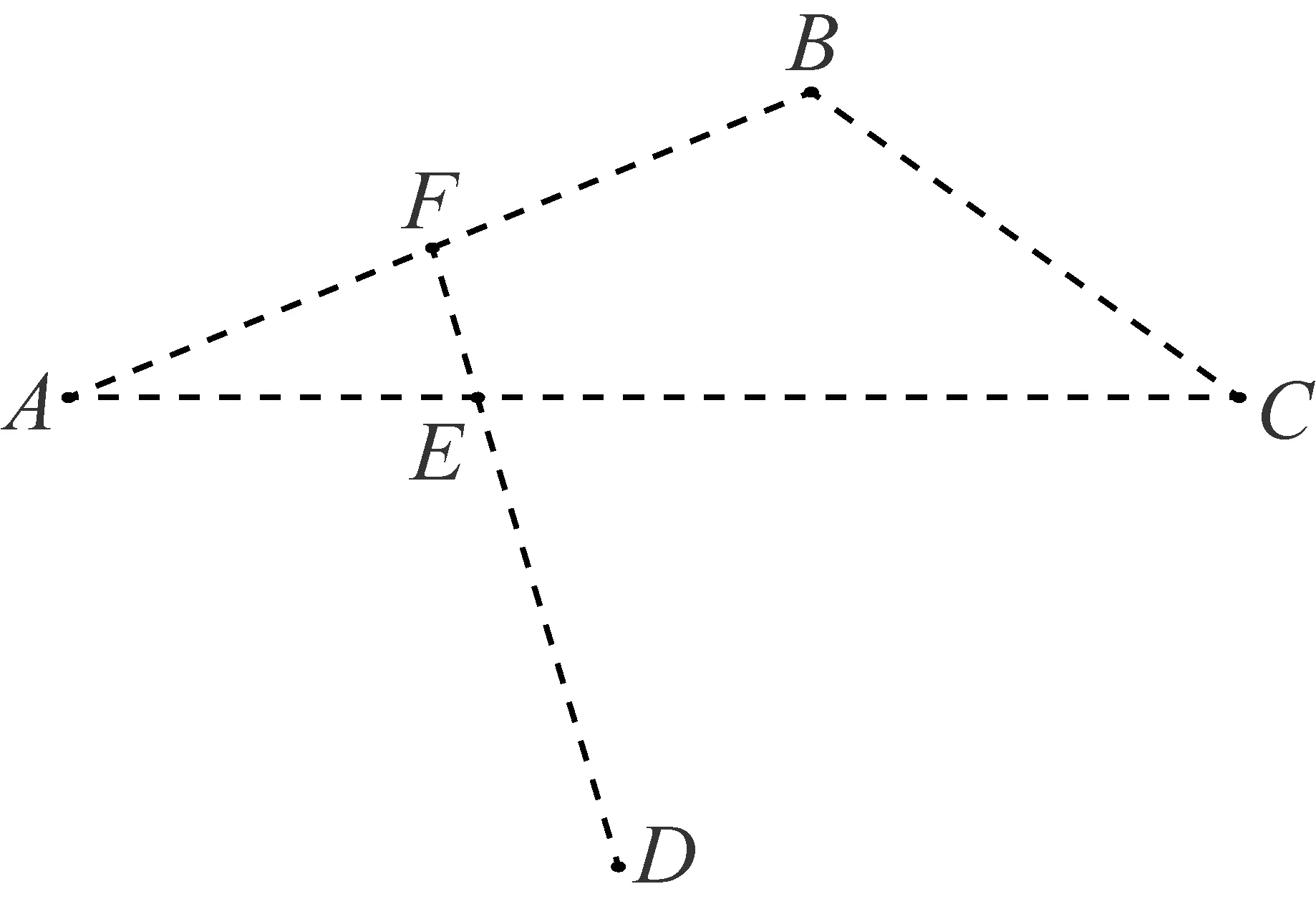
图7

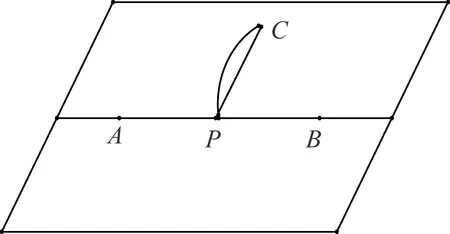
图8

Schuyler在其《几何基础》(1876)[10]中采用了另一方式.他首先证明：经过一条直线有无数个平面.事实上，在一个平面上作一条直线，以它为轴，平面可以旋转到任何位置.

Wilson在其《立体几何与圆锥曲线》(1880)[11]中利用旋转确定平面的存在性，然后用反证法证明平面的唯一性.如图8，若有两个平面经过点A，B，C，则对于AB上的任一点P，从C点可以作两条直线CP，每个面上各一条，这是不可能的，从而证明了唯一性.

但上述方法似乎也不能完全让人满意，数学家还需要寻找更好的方法来处理这一问题.

4　从定理到公理转变的阶段

19世纪末，一个显著的进步在几何中发生，希尔伯特在其《几何基础》中建立了完全公理化的欧氏几何.在这之前，意大利数学家皮亚诺(G. Peano, 1858～1932)创立数学学派，对算术和几何的公理化做出了巨大的贡献，其中的一名重要成员、意大利数学家皮埃里(M. Pieri, 1860～1913)利用点、线段和运动对几何进行公理化.他将平面定义为：“给定不共线三点A，B和C，则面ABC可以由A与BC上各点，B与CA上各点，C与AB上各点所连接的直线全部填满.”另一方面，希尔伯特可能受数学抽象化和公理化趋势的影响，并没有定义平面，而将其作为一个基本的概念，像点和直线一样，公理决定了基本概念之间的联系，概念的意义只有在公理中得到体现，因此，公理就起到了定义的作用.希尔伯特的公理被大部分数学家所接受，同时也被数学教育界所接受，从而影响了大多数教科书.在这一阶段，开始出现将平面概念作为原始概念，将平面的有关命题作为公理的趋势，平面包含式定义和勒让德的定理2变成了公理，今日人教版教科书中的公理1和公理2开始出现.

Newcomb在《几何学基础》(1884)[12]中不再定义平面，转而直接给出以下公理：

公理1如果直线上有两点在平面上，则整条直线在平面上.

公理2经过一条直线有无数个平面，且平面可以直线为轴旋转.

公理3只有一个平面可以经过一条直线和直线外一点.

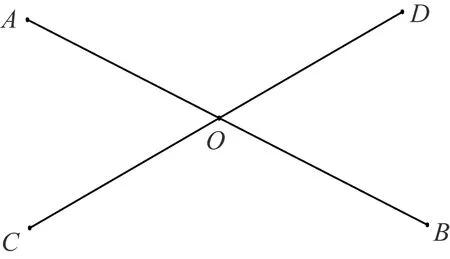
图9

接下来，Newcomb利用上述公理证明：“两条相交直线确定一个平面”.如图9，AB和CD交于点O.让任意平面经过直线AB，将平面绕AB旋转直到经过点C(Newcomb的公理2)，因点C和O在直线CD上，故CD也在同一平面上(Newcomb的公理1).由Newcomb的公理3可知，这个平面是唯一的.Newcomb又证明：“两平面的交线为直线.”证法与普雷菲尔等的方法相同.

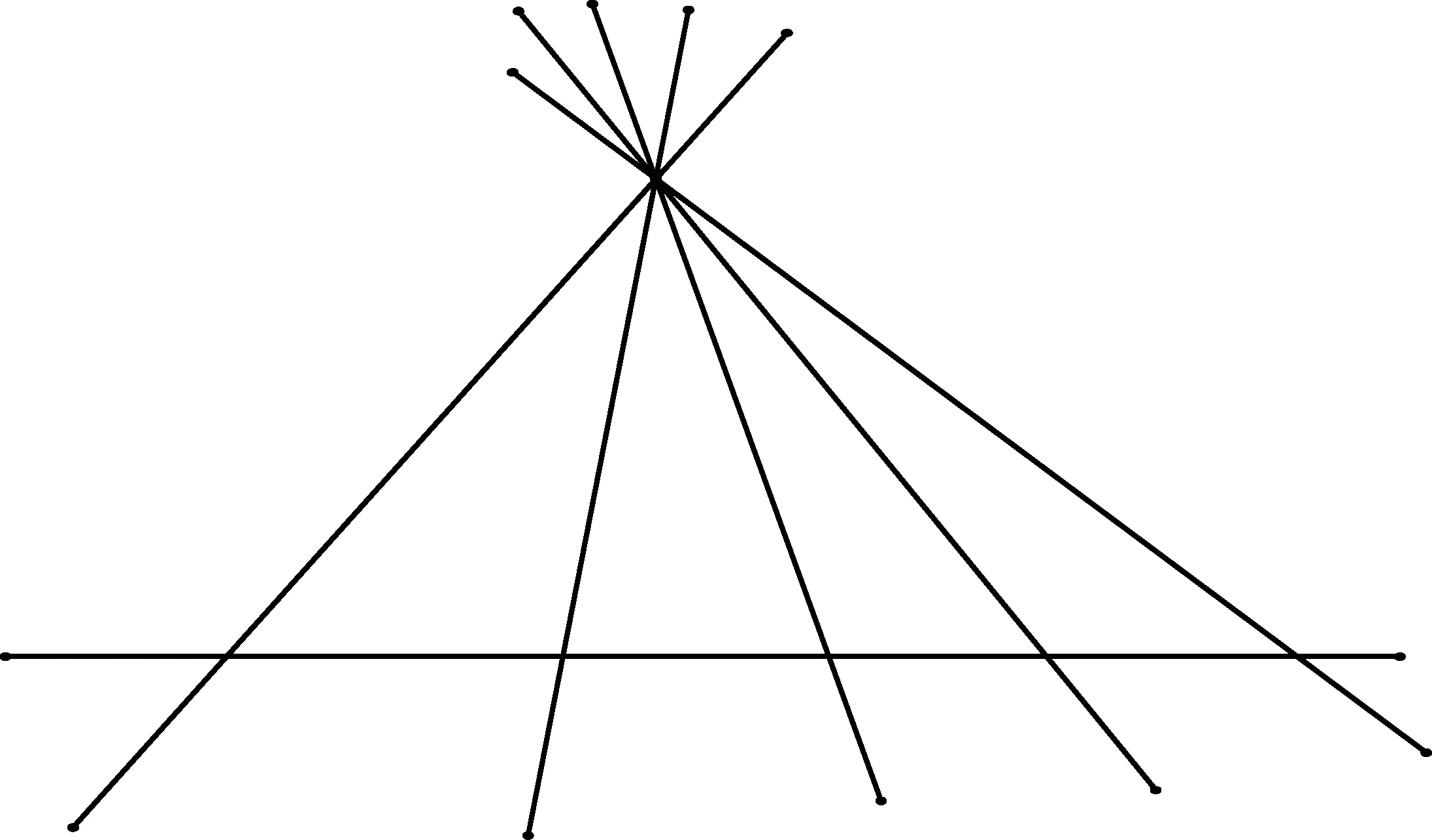
图10

Halsted在《几何基础》(1885)[13]中给出了与克雷尔类似的定义：如图10，一个平面是由经过定点与定直线上的点的直线运动而形成的.

需要指出的是，人教版中的公理1和公理2在这一时期的大部分教科书仍未以公理形式出现.Bartol在其《立体几何基础》(1893)[14]中仍采用平面的包含式定义.先证明定理：“过一条直线有无数个平面”，由此推出勒让德的定理2和定理3.Thompson在其《立体几何和测量几何基础》(1896)[15]中仍采用与Tappan类似的方法证明平面的唯一性.

不同教科书采用的公理也互有不同.Keigwin在《几何基础》(1897)[16]中将“不共线三点确定一个平面”作为公理.Hart和Feldman在《平面与立体几何》(1912)[17]中将“直线与平面最多交于一点”作为公理.Richardson在《立体几何》(1914)[18]中将“若两平面有一个公共点，则它们有第二个公共点”作为公理.此外，Durell在《立体几何》(1904)[19]中将公理称为平面在空间中的基本性质或立体几何的公设，而不称为公理.

5　三大公理的最终形成阶段

从1920到1960，到了这一时期，平面作为不加定义的概念，平面公理已经普遍出现于几何教科书中.值得注意的是，这一时期，在勒让德定理3的证明中，“为什么两个平面相交有两个交点”这一问题开始出现，因此，该定理逐渐被当作公理.Hawkes，Lucy和Touton在《立体几何》(1922)[20]中，首先将“若两平面有一个公共点，则它们有第二个公共点”作为公设，然后再证明定理3，Cowley的《立体几何》(1934)[21]中将“两平面相交，交线为直线”作为公理，从而《几何原本》中的三个命题终于都成了公理.

可以看出，希尔伯特的公理化方法对这一时期平面概念的呈现方式产生了深刻的影响，且人教版教科书中平面的三公理在这一时期的教科书中有了基本的雏形.

6　结语

从以上考察中我们可以发现，平面的概念与公理有着漫长的历史发展过程，初步发展时期巴门尼德和欧几里得等对平面的认识接近于我们的直观感受，定义中有很多模糊的词语，因此不能将定义用于命题的推理中，到了平面的构造性阶段，辛松、克雷尔、傅里叶等人基于定义的简洁性与可推理的特征给出一些平面的构造性定义，最后辛松的定义被之后的大部分教科书认可，平面有关的命题开始采用这一定义进行了初步的证明，但其中仍然具有一些逻辑上的问题，因此，不少数学家在辛松定义的基础上尝试各种办法加以改善，但总是不能完全解决疑问，最后在历史的趋势下，希尔伯特的公理化方法出现，定义与逻辑的问题最终得到解决，平面的定义与公理也终于出现了现代定义的雏形.

今日教科书中的平面三公理也经历了漫长的发展过程，其雏形首先在《几何原本》中以命题形式出现.之后，人教版中的公理1以定义形式出现，其余两个公理由该定义推出.之后，包含式定义和勒让德的定理2率先以公理形式出现，即人教版的公理1和公理2.最后，勒让德的定理3成了今天的公理3.

平面概念的历史有着重要的教育价值.今日教科书将平面视为原始概念，并不是由于这是一个易于理解的简单概念，而是漫长历史演进的结果.在教学中，让学生经历这一过程有利于他们对平面概念本质的理解.历史表明，平面三公理与平面概念是互相促进、共同发展的，可以说，正是由于平面这三个公理的各种问题促进了平面概念的不断完善，在教学中可以有效利用这一点促进学生对平面概念的深刻理解.同时，在历史上，这三个公理作为定理时，它们之间存在一定的逻辑关系.作为公理之后，逻辑关系似乎消失了，让学生了解这一点，可以让学生更深刻地解三个公理之间的联系.