Dandelin双球之问*
昌 明
(扬州市教育科学研究院 225007 )
苏教版《数学(选修2-1)》2.1节“圆锥曲线”中首先提出问题:用平面截圆锥面还能得到哪些曲线?这些曲线具有哪些几何特征?进而展开了对圆锥曲线概念的研究,并用Dandelin双球证明了椭圆情形.本节教学内容中,在圆锥面和截面之间嵌入双球是证明定理的关键,也是师生感到困惑的教学难点.教师对这一节的处理由于对教材研究不透只能照本宣科,学生对突然嵌入的双球也感到迷茫,从而大大降低了本节教学内容的教育价值.
当然,我们并不能确切地知道Dandelin是如何想到嵌入双球的,不过,我们可以作一些合情的猜想,探索嵌入双球的合理性,这对于培养学生的探究意识、质疑精神,充分彰显本节教学内容的教育价值具有积极意义.
1 对圆锥曲线认识的发展
圆锥曲线早在古希腊时代就已经被发现和研究.柏拉图学派的梅内赫莫斯(Menaechmus,约公元前360)为解决倍立方体问题而发现了圆锥曲线.[1]后来,阿波罗尼奥斯(Apollonius of Perga,约公元前262~约公元前190)在前人工作的基础上创立了完美的圆锥曲线理论.[2]《圆锥曲线论》用纯几何的手段达到了今日解析几何的一些主要结论,对现今双曲线、椭圆的轨迹定义也作了研究,不过,只是作为“双曲线和椭圆的焦点性质”,且用多个命题进行了证明.在16世纪之前人们只是出于对纯数学的兴趣来研究圆锥曲线,而且是用静态的观点来研究图形的性质的,即把它们看做是用平面从不同角度截割锥体所得到的曲线,[3]从而得到了圆锥曲线的截线定义.《圆锥曲线论》所取得的成就令人惊叹,但是,这种单一的纯几何形式也使其后大约两千年间的几何学裹足不前.文艺复兴以来资本主义生产力的发展,对科学技术提出了全新的要求:机械的普遍使用引起了对机械运动的研究;世界贸易的高涨促使航海事业的空前发达,而测定船舶位置问题要求准确地研究天体运行的规律……总之,到了16世纪,对运动与变化的研究已变成自然科学的中心问题.[1]行星绕日运动和抛体运动要求人们用运动和变化的观点研究圆锥曲线,人们不再将圆锥曲线看成是依附在圆锥面上的静态曲线,而是自然界物体运动的普遍形式,将圆锥曲线看成是满足某种条件的动点运动轨迹更能描述自然界的变化规律.
17世纪,法国数学家笛卡儿《方法论》的问世标志着解析几何的产生,笛卡儿批判地继承前人的成就,把传统数学中对立着的两个研究对象“数”与“形”统一了起来,并在数学中引入了变量的思想,这是数学史上的一个划时代的变革.解析几何的诞生洞开了人们的思维,为研究圆锥曲线开辟了一条崭新道路.
在历史的长河中,人们对圆锥曲线认识发展:从截线定义到轨迹定义,从静态观点到运动变化观点,从纯几何方式到数形结合的思想,反映了社会的发展,人类对自然界认识的进步.正如笛卡儿的一句名言“我思故我在”所表达的,无论是“日心说”观念的确立,还是《方法论》的问世,都是怀疑传统与权威、大胆思索创新精神的结晶.
2 Dandelin双球之猜想
2.1 Dandelin双球之猜想
1822年,比利时数学家旦德林(Germinal Pierre Dandelin,1794—1847)在一篇论文中利用圆锥曲线的两个内切球,直接在圆锥曲线上导出椭圆的焦半径性质,从而证明了截线定义与轨迹定义的统一性,两个内切球称为Dandelin双球.Dandelin双球是如何产生的?对这一问题的猜想离不开历史背景、旦德林工作经历和数学思维规律.
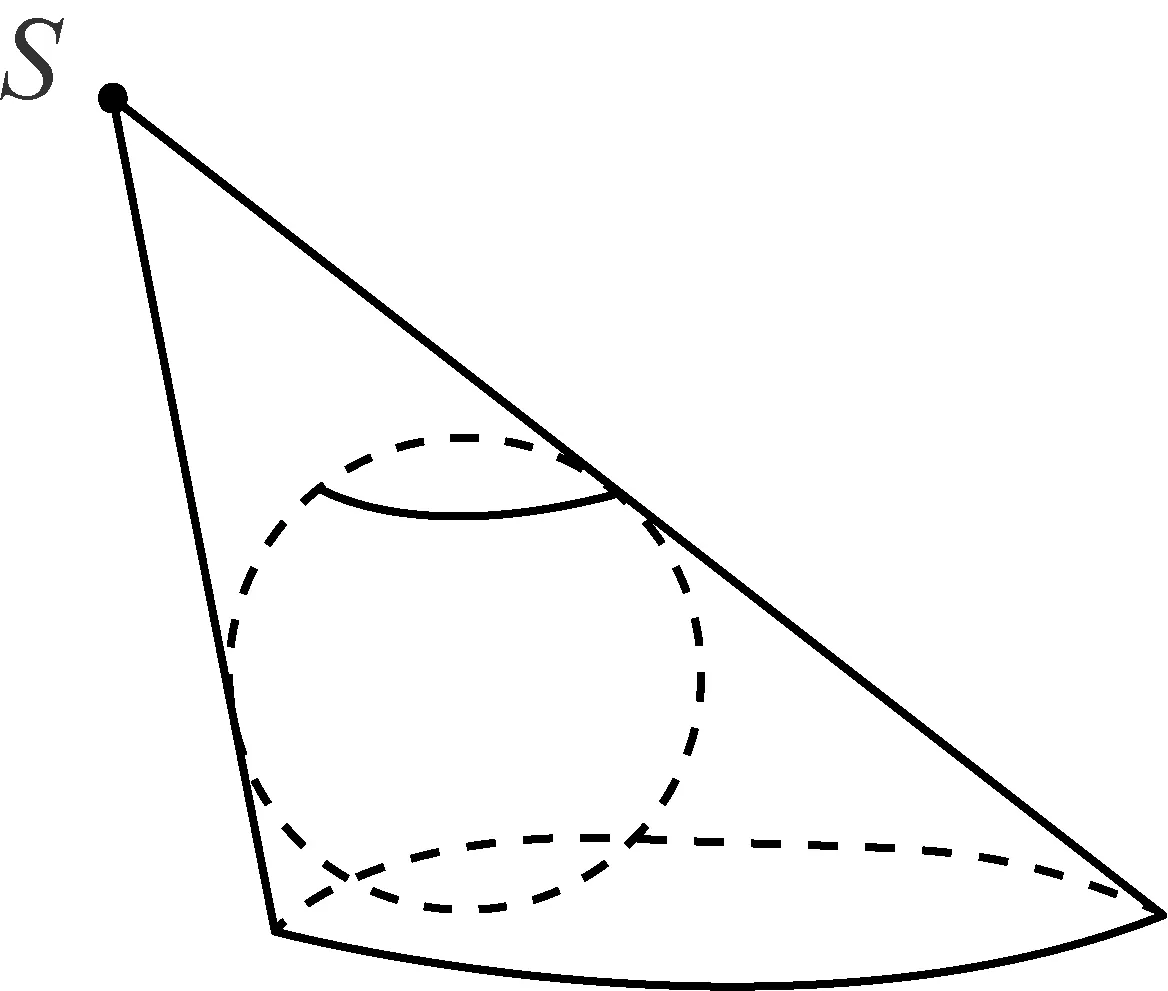
图1
18世纪末与19世纪初,蒙日的《画法几何学》以及蒙日学生卡诺等人的工作,重新激发了人们对综合射影几何的兴趣.[1]由于射影几何与锥面有着天然的联系,也被用于圆锥曲线的研究.旦德林正是那个时代的数学家,他从事于立体投影,代数及概率研究,一个可能触发旦德林灵感的是对球的投影研究.如图1,观察一个球在点光源S的照射下的投影,当点光源S的位置变化时,投影是一些连续变化的圆锥曲线.这一自然现象也暗合了古希腊人关于圆锥曲线的研究,把与球相切的光线看成圆锥面,投影看成截面,这就形成了截面截圆锥产生圆锥曲线的情形.现在要做的工作是能用圆锥曲线的轨迹定义来证明截线是圆锥曲线,下面以椭圆为例进行研究.证明的关键是要找到焦点,从以上的分析中可以看到球对圆锥曲线所产生的影响,点S光源的位置变化也可以看成是球的位置的变化.德国天文学家开普勒研究天体运行轨道时发现:椭圆、抛物线、双曲线、圆以及由两条直线组成的退化圆锥曲线,都可以从其中一个连续地变为另一个,只须考虑焦点的各种移动方式.从这一角度思考,球应与圆锥曲线的焦点有关.而球在投影面上只有一个点,即切点,因而,猜测切点是焦点是合理的猜想.现在,我们将圆锥放置成正圆锥形状,如图2.事实上,那个时代的人已经知道,线段AB是椭圆的长轴,其中点是椭圆中心,两个焦点在长轴上并关于椭圆中心对称.根据对称性思想,猜想另一个焦点很可能也是一个球与锥面、截面都相切且在截面上的切点,从而,依据数学的思维规律猜想出另一个内切球和焦点,如图3.对证明的探索将在教学设计中研究.
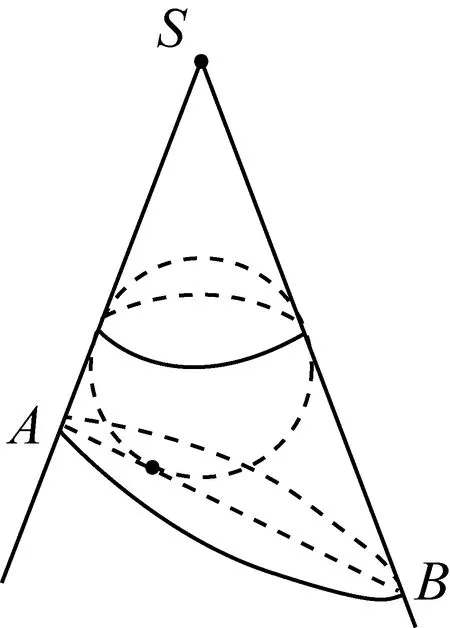
图2
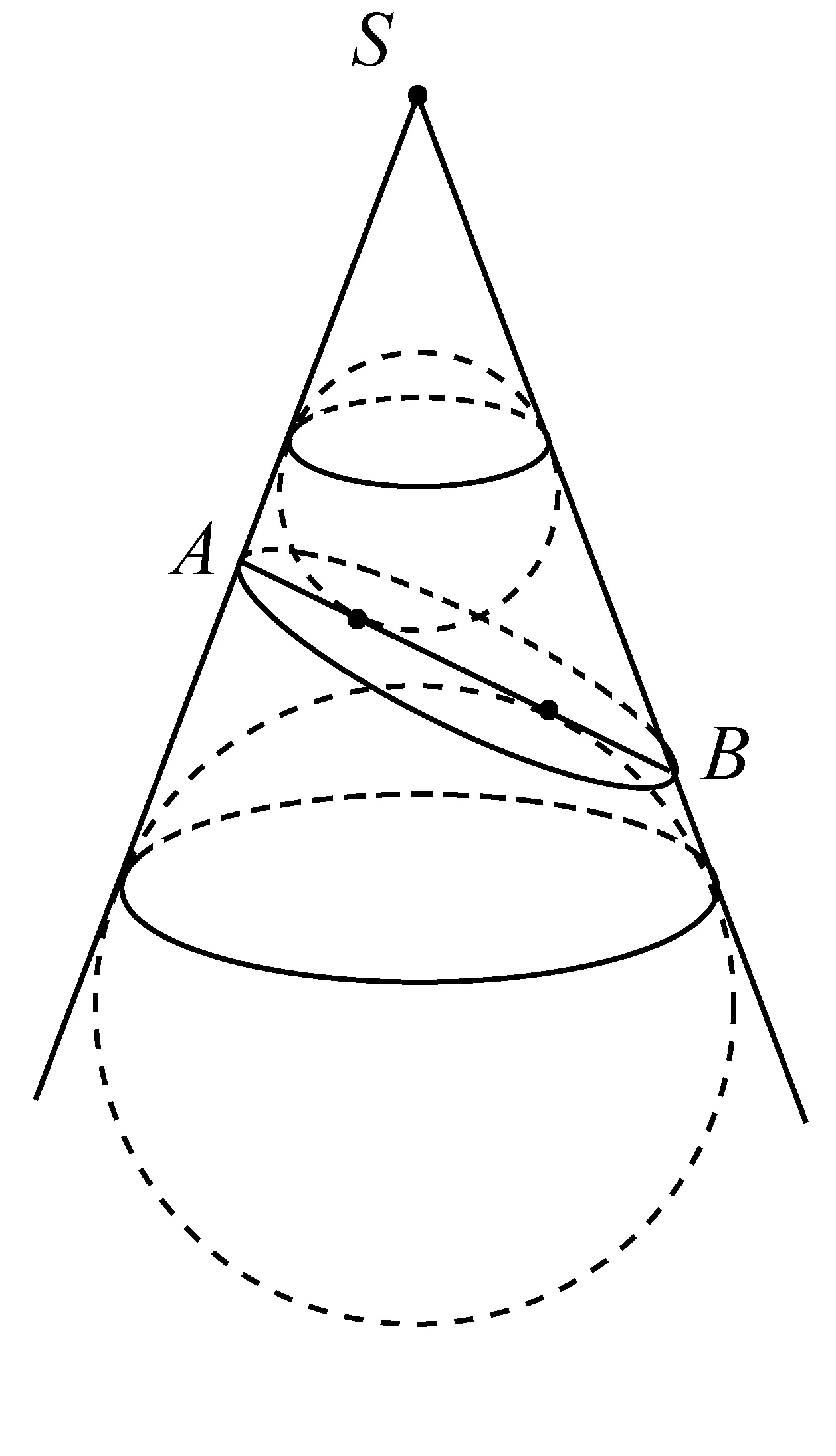
图3
旦德林用在圆锥面和截面之间嵌入双球证明圆锥曲线的截线定义与轨迹定义的等价性定理也称为冰淇林定理,定理的表述中将圆锥比作蛋筒,截面比作饼干.或许,旦德林在紧张的工作之余品尝冰淇林时获得了嵌入双球的灵感,这也是一种双球产生的可能.
Dandelin双球的产生还有一种可能是来自于对平面几何的研究.图3的轴截面是三角形SAB和其内切圆和一个旁切圆,反过来,将这一平面图形立体化即是图3.因而,猜测旦德林在研究平面图形中获取了双球灵感也是一种合理的猜想.
当然,以上的三种猜测仅仅是一种合情猜想,探究双球的产生是为了更好地学习圆锥曲线.
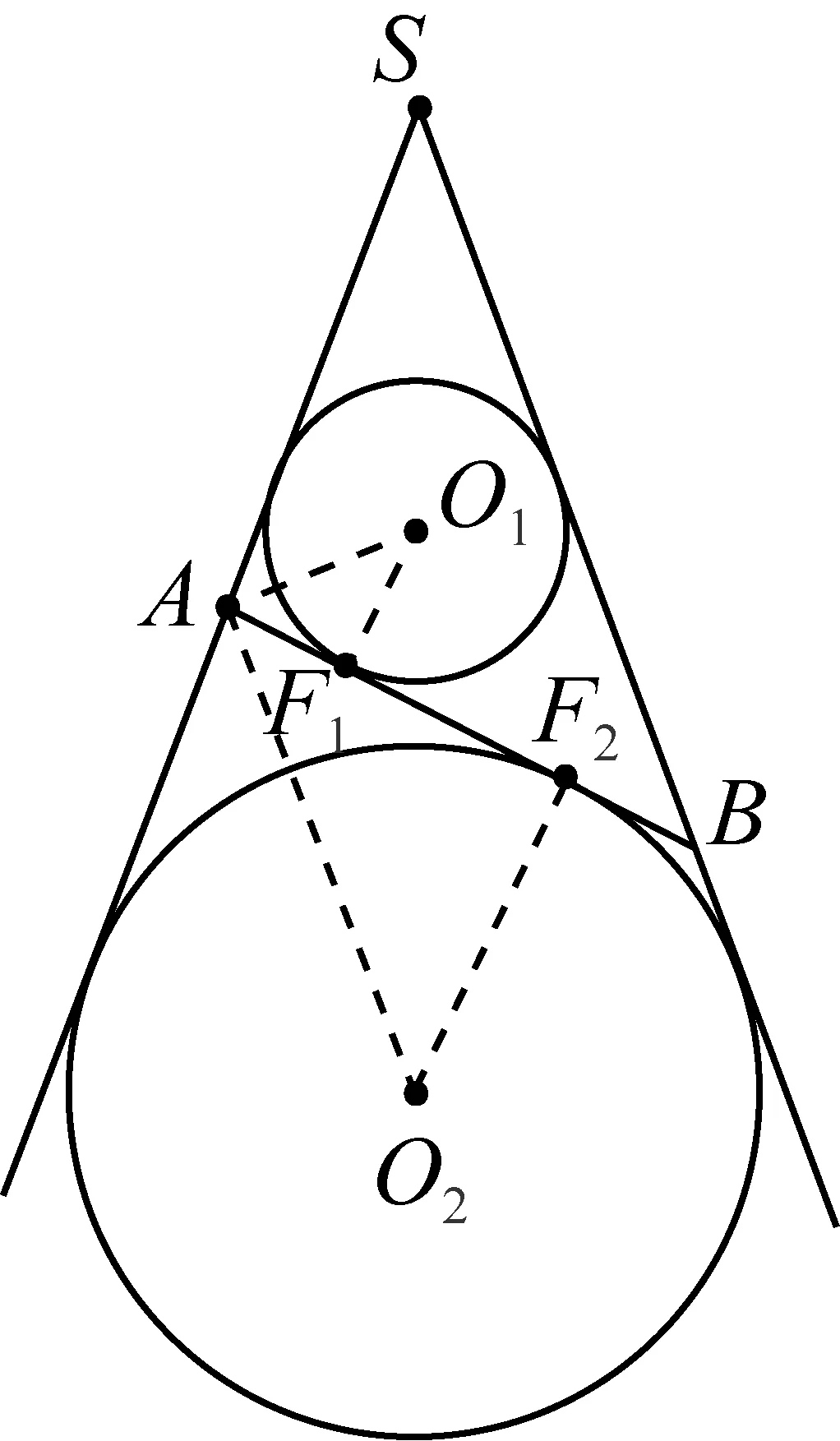
图4
2.2 Dandelin双球的再思考
笔者在研究Dandelin双球产生的过程中,一直在思考一个问题:Dandelin双球与圆锥曲线的焦点有关,还与圆锥曲线中哪些量有关呢?
如图4,这是图3的轴截面,O1、O2分别是两个内切球的球心,F1、F2分别是两个内切球与截面的切点,也是截得的椭圆曲线焦点.由Rt△AF1O1∽Rt△O2F2A得AF1·AF2=O1F1·O2F2,设椭圆长轴长、短轴长、焦距分别为2a、2b、2c,则AF1=a-c,AF2=a+c,从而有O1F1·O2F2=(a-c)·(a-c)=b2,也就是说,椭圆的短半轴长是两个内切球半径的等比中项.
同理,对于双曲线,双曲线的虚半轴长是两个内切球半径的等比中项,证明略.
3 基于猜想的教学设计
苏教版在“圆锥曲线与方程”的处理上采用了先合后分的方法,即先总体介绍圆锥曲线的概念,再分别用解析法研究椭圆、双曲线、抛物线.在开始的2.1节“圆锥曲线”中由一个平面截圆锥面引出三条曲线:椭圆、双曲线、抛物线,并用Dandelin双球证明了椭圆情形,从而得出圆锥曲线的轨迹定义.由此,我们不难看出,Dandelin双球是联系截线定义与轨迹定义的纽带.因而,本节课的设计应把重点放在Dandelin双球的发现上,并触及人们对圆锥曲线认识的发展,培养学生的探究意识、质疑精神.下面是苏教版《数学(选修2-1)》2.1节“圆锥曲线”的简要教学设计:
情境设置,点击历史
在公元前3世纪前后,古希腊学者梅内赫莫斯、欧几里德、阿基米德、阿波罗尼奥斯等发现并研究了一类曲线:用一个平面截圆锥面所得到的曲线.很显然,当平面经过圆锥面的顶点时,可得到两条相交直线;当平面与圆锥面的轴垂直时,截得的图形是一个圆.用平面截圆锥面还能得到哪些曲线?这些曲线具有哪些几何特征?
结合实物模型让学生观察、猜想.
观察实验,建立联系
实验观察,一个球在点光源S的照射下的投影(如图5),当点光源S的位置变化时,投影有哪些变化?(也可以布置学生课前完成,课上交流.课上教师需借助多媒体演示实验,以增强观察的效果.)

图5
学生交流后,教师再提问:这一生活实例与古希腊人用平面截圆锥面的模型有联系吗?
设计说明:培养学生观察大自然、研究大自然的意识,并通过与古希腊人用平面截圆锥面的模型建立联系,帮助学生将点光源照射球所得投影的生活实例抽象成“用平面截圆锥面”的数学模型.
活动探究,建构数学
(仅对椭圆情形进行研究.)
问题1:当点光源S在球的正上方时投影的轮廓是什么图形?投影的轮廓上的点有什么性质?(圆,圆上的点到圆心(切点)的距离是一个定值.)
缓慢地移动点光源S,投影的轮廓变成了椭圆,提问(问题2):椭圆上点有何性质?学生发现,椭圆上的点到切点的距离不是一个定值.引导学生质疑:只是稍稍移动点光源S,圆变为椭圆,椭圆上的点就没有类似的性质吗?(显然,椭圆上的点到切点的距离不是一个定值.)
问题3:(教师一边演示左右改变点光源S的位置,切点左右摆动,一边提问)圆和椭圆都是轴对称、中心对称图形,投影的轮廓是圆时,切点是圆的中心;投影的轮廓是椭圆时,切点偏在一侧,你有何猜测?
引导学生由椭圆的对称性猜想:椭圆中还有一个关于椭圆中心的对称点,它应该也是一个球与截面、锥面都相切且在截面的切点,如图6.
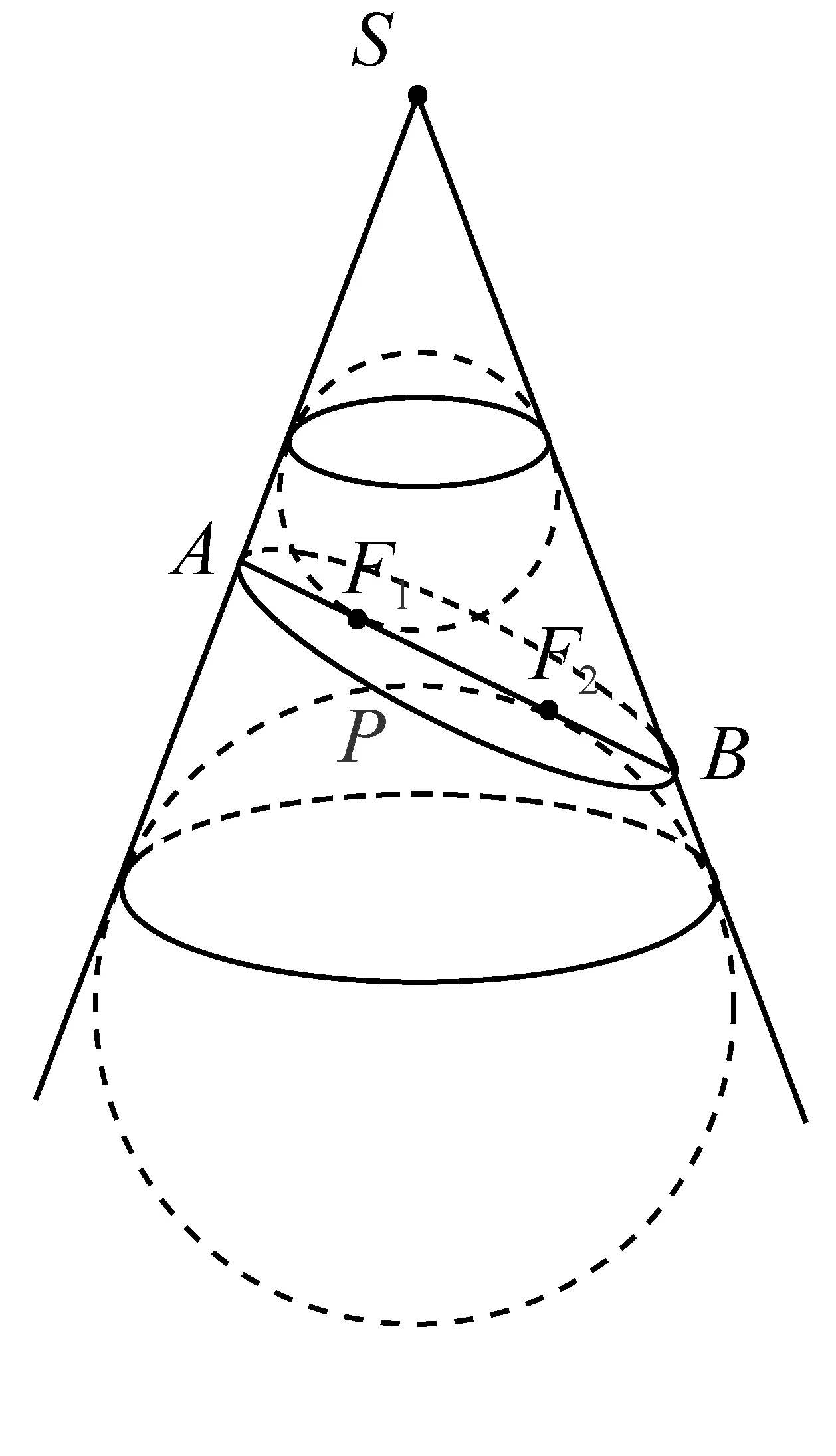
图6
问题4:如图6,当点P在椭圆上移动时,点P与切点F1、F2的连线段PF1、PF2,关于PF1、PF2的长类比圆上点的性质有何猜想?
引导学生观察:当点P在椭圆上移动时,点P与切点F1、F2的连线段PF1、PF2一长一短地交替变化着,猜想:PF1与PF2的和是一个定值.
问题5:这个定值是什么呢?我们先研究特殊位置.当点P在点A处,PF1与PF2的和是什么?(如图7).
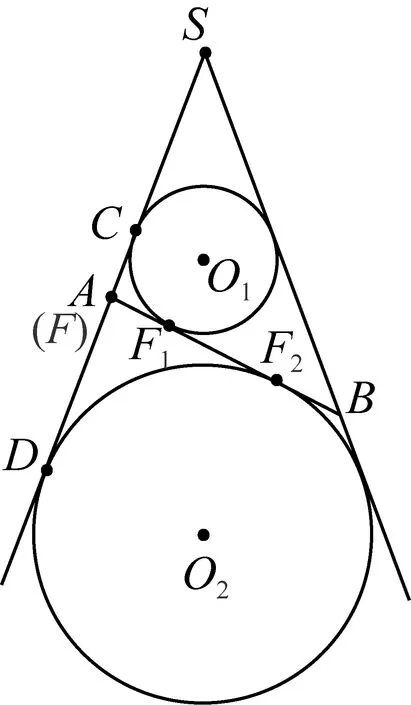
图7
引导学生得出:PF1+PF2=AB,PF1+PF2=PC+PD=CD.
问题6:AB、CD是一个定值,请回顾一下是利用什么定理证明PF1+PF2=AB=CD的?(切线长定理)
目前计算机基础课程主要分两个学期开设,大一上学期开设计算机文化基础,下学期开设程序设计类课程。主要存在以下问题:1.课程设置体系性不强,课程门数少,内容结构安排简单。2.程序设计类课程没有体现专业特色和培养目标;所选择的程序设计语言或陈旧过时(如VB语言),语法繁多、调试困难,不适合没有任何编程基础的非计算机专业学生学习(如C语言)。3.后续课程缺失。课程结束后,学生无法进一步学习更多的计算机相关技术。
问题7:当点P在其他位置时,PF1+PF2与AB、CD相等吗?如何证明?
问题8:如果我们要证明PF1+PF2=CD,现在遇到什么困难?
学生发现:PF1、PF2与CD分开了,P点不在CD上了,不好直接使用切线长定理.
问题9:能否移动CD使CD经过P点,这样便于使用切线长定理?
引导学生移动CD:过P作圆锥面的一条母线分别与两球相切于点M、Q,MQ=CD(如图8),并完成定理证明.
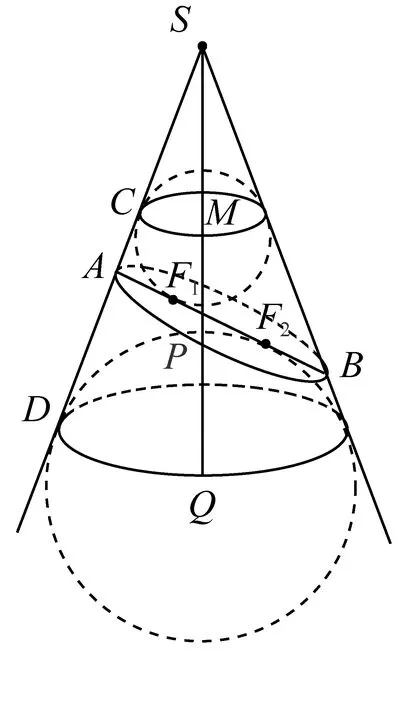
图8
建构椭圆的轨迹定义,以下略.
反思总结,深化研究
本节课主要研究了圆锥曲面上的截线的几何特征并给出了证明,这个证明是比利时数学家旦德林于1822年发现的,他巧妙地在圆锥面和截面之间嵌入双球直接在圆锥上推导出椭圆上点的几何特征,从而证明了圆锥曲线的截线定义与轨迹定义的一致性.然而从圆锥曲线的截线定义到轨迹定义经过了大约两千年,请同学们课后查阅相关资料,深入研究圆锥曲线的发展史,下节课交流.
下节课用一部分时间交流,向同学们介绍本文中的“圆锥曲线的发展历史”,培养学生主动学习、探究的意识和学习数学的兴趣.
4 结束语
《普通高中数学课程标准(实验)》指出:“数学课程‘要讲推理,更要讲道理’,通过典型例子的分析和学生自主探索活动,使学生理解数学概念、结论的形成过程,体会蕴涵在其中的思想方法,追寻数学发展的历史足迹,把数学的学术形态转化为学生易于接受的教育形态.[6]”数学教师要充分挖掘教学内容中所蕴含的思想方法、文化价值等丰富的内涵,充分彰显数学的教育价值,全面贯彻以人为本的新课改教学理念.

