ON THE UNIT GROUPS OF THE QUOTIENT RINGS OF IMAGINARY QUADRATIC NUMBER RINGS

WEI Yang-jiang,SU Lei-lei,TANG Gao-hua

(School of Mathematics and Statistics,Guangxi Teachers Education University,Nanning 530023,China)

Abstract:In this paper,we investigate the unit groups of the quotient rings of the integer rings Rdof the quadratic fieldsover the rational number field Q.By employing the polynomial expansions and the theory of finite groups,we completely determine the unit groups of Rd/⟨ϑn⟩for d= −3,−7,−11,−19,−43,−67,−163,where ϑ is a prime in Rd,and n is an arbitrary positive integer.The results in this paper generalize the study of the unit groups of Rd/⟨ϑn⟩for d=−1,which obtained by J.T.Cross(1983),G.H.Tang and H.D.Su(2010)and for the case d=−2 by Y.J.Wei(2016).

Keywords: imaginary quadratic number ring;quotient ring;unit group;quadratic field

1 Introduction

Throughout this paper,we denote by Z the set of rational integers,Znis the additive cyclic group of order n,Z/⟨n⟩is the ring of integers modulo n,and o(θ)is the order of θ in a group.For a given ring R,let U(R)denote the unit group of R,let⟨γ⟩denote the ideal of R generated by γ ∈ R.If γ is an element of a given group G,we also use ⟨γ⟩to denote the subgroup of G generated by γ∈G.The Legendre symbol(),where a is an integer,p is a prime and p-a,is defined as follows:if there exists an integer x such that x2≡a(mod p),then()=1,otherwise,()=−1.

Lemma 1.1[8,Lemma 2.4.2]The ring Rdof algebraic integers of K=is

(1)Rd={a+:a,b∈Z},if d≡2,3(mod 4).

(2)Rd=:a,b∈Z are of the same parity},if d≡1(mod 4).

By Lemma 1.1,for d= −3,−7,−11,−19,−43,−67,−163,the elements of Rdare all of the formwhere a,b∈Z are of the same parity.Moreover,we know that U(Rd)={±1}for all d= −3,−7,−11,−19,−43,−67,−163.

Now,we need to identify all primes in the ring Rd.The following theorem is obtained from[9,Theorem 9.29].

Theorem 1.2 For d= −3,−7,−11,−19,−43,−67,−163,up to multiplication by units,the primes of Rdare the following three types(D=−d):

(1)p,where p∈Z is a prime satisfying the Legendre symbol()=−1;

(3)δ=

2 Main Results

Throughout this section,d= −3,−7,−11,−19,−43,−67,−163.For conveniences,we denote by D= −d.Let n be a positive integer,and ϑ is a prime in Rd.We determine the structure of unit groups of Rd/⟨ϑn⟩.

First,we characterize the equivalence classes of Rd/⟨ϑn⟩,where ϑ is prime in Rd.For α ∈Rd,we denote by[α]∈ Rd/⟨ϑn⟩the equivalence class which α belongs to.Simultaneously,we make corrections to the equivalence classes which are given in[6,Theorem 3.2]for the case d=−3.

Theorem 2.3 Let ϑ denote a prime of,δ=,D=−d.For an arbitrary positive integer n,the equivalence classes of Rd/⟨ϑn⟩are of the following types:

(4)Rd/⟨πn⟩={[a]:0 6 a 6 qn−1,a ∈ Z},where q=is a prime in Z satisfying the Legendre symbol

(5)Suppose that d ≠ −7.Then

(b)For n>2,Rd/⟨2n⟩=R1∪ R2∪ R3,where

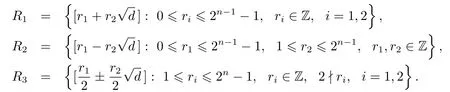
Proof(1)As δ2m=dm,we get that ⟨δ2m⟩= ⟨Dm⟩.Supposewhere a1,a2∈Z.Let ai=Dmki+riwith 0 6 ri6 Dm−1,ki∈Z,i=1,2.ThenSo α and r1+belong to the same equivalence class of Rd/⟨δ2m⟩.

(2)As δ2m+1=dmδ,we get thatSupposewhere a1,a2∈Z.Let a1=Dm+1k1+r1with 0 6 r16 Dm+1−1.Let a2=Dmk2+r2with 0 6 r26 Dm−1.ThenSo α andbelong to the same equivalence class of Rd/⟨δ2m+1⟩.

Finally,it is easy to verify that the classes of(2)are distinct.

(3)It can be proved with the similar method to(1).Suppose where a1,a2∈Z.Let ai=pnki+riwith 0 6 ri6 pn−1,ki∈Z,i=1,2.ThenSo α andbelong to the same equivalence class of Rd/⟨pn⟩.

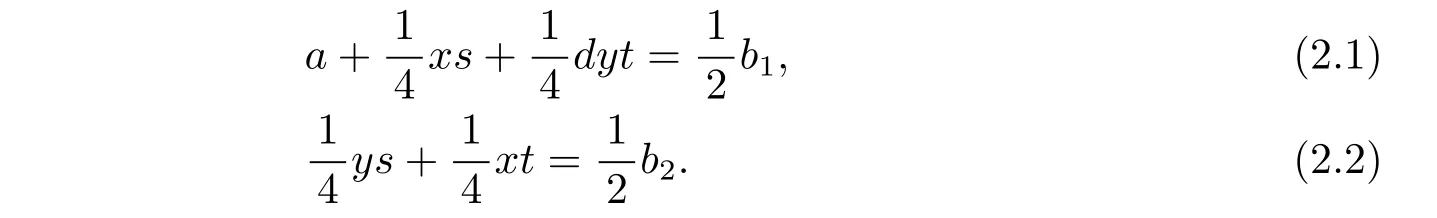
Now we solve the integer a from the above equations.By equation(2.1),we obtain

And by equation(2.2),we get−dyts−dt2x=−2b2dt.Eliminating dyts between this equation and(2.3),we obtain

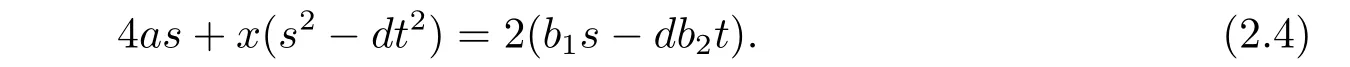
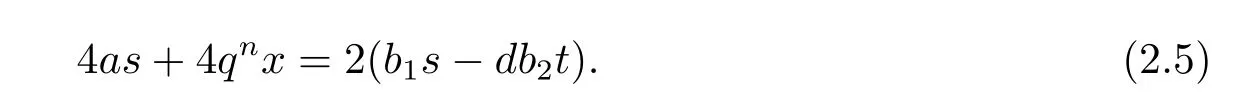
Moreover,since s,t∈Z are of the same parity and b1,b2∈Z are of the same parity and note that d is odd,we derive b1s−db2t is even.Hence,equation(2.5)can be written aswhich implies that

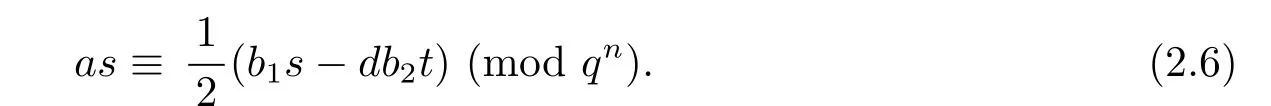
Finally,it is easy to verify that the classes of(4)are distinct.

(5)Suppose d ≠ −7.

(a)We first determine the structure of the quotient ring Rd/⟨2⟩.Suppose α1=a ∈ Z.If a is even,then∈ Rd.It follows from α1=0+2×that α1belongs to the equivalence class[0]in the quotient ring Rd/⟨2⟩.If a is odd,then a=1+2k for some k ∈ Z.Then clearly α1belongs to the equivalence class[1].

Suppose α2=,where b∈Z.If b is even,then∈Rd.We have

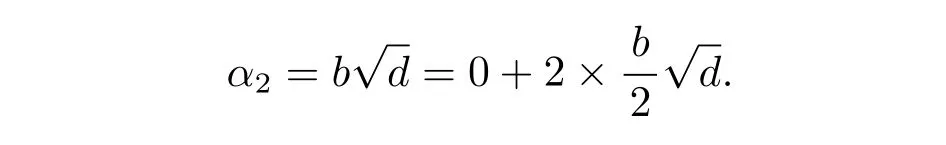
So clearly α2belongs to the equivalence class[0].If b is odd,then

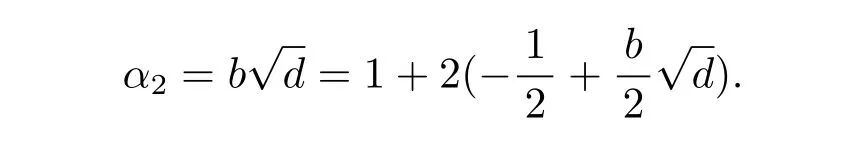
Therefore,α2belongs to the equivalence class[1].

Finally,we show that the classes of(5)(a)are distinct.Clearly

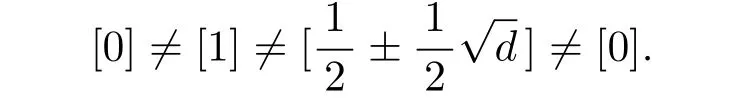
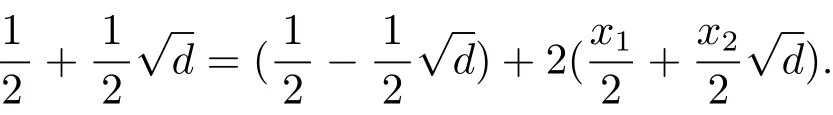
Clearly,the above equation holds if and only if x1=0 and x2=1,which is impossible,since x1,x2∈Z must be of the same parity.Hence,we conclude thatTherefore,the classes of(5)(a)are distinct.

(b)Now,let n>2.We determine the structure of the quotient ring Rd/⟨2n⟩.Supposewhere a1,a2∈ Z.Let ai=2n−1ki+ri,ki,ri∈ Z,and 0 6 ri6 2n−1−1 for i=1,2.First,if k1and k2are of the same parity,thenMoreover,sincewe conclude that β1and r1+r2belong to the same equivalence class in the quotient ring Rd/⟨2n⟩.Secondly,if k1and k2are not of the same parity,thenSincewe obtain that β1and r1− (2n−1− r2)d belong to the same equivalence class.Furthermore,since 0 6 r26 2n−1− 1,we derive that 1 6 2n−1− r26 2n−1.So in the second case,i.e.,k1and k2are not of the same parity,we get that β1andbelong to the same equivalence class,whereand

Finally,we claim that the classes of(5)(b)are distinct.We only show that

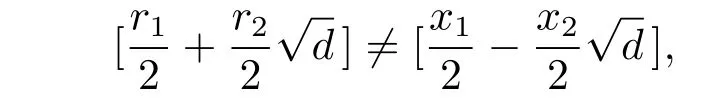
where ri,xi∈ {1,3,···,2n−1}with 2-rixifor i=1,2.Indeed,ifthen there exit t1,t2∈Z of the same parity such that

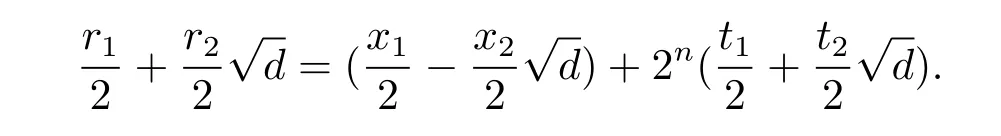
So we obtain r1=x1+2nt1and r2=−x2+2nt2.It is easy to show that t1=0 and t2=1,which is a contradiction.

Example 2.4 To illustrate the case d=−19,q=23=and n=2,let γ=where b1=3 and b2=1.We give the equivalence class in Rd/⟨π2⟩which γ belongs to.Sinceis a proper factor of q in Rd,Denoted by s=−30,t=−8.Substituting the values for s,t,b1,b2,d,q and n into congruence(2.6),we get that a=198 is a solution to congruence(2.6).Moreover,substituting the values for a,s,t,b1,b2and d into equations(2.1)and(2.2),we have x=11 and y=−3.Therefore,

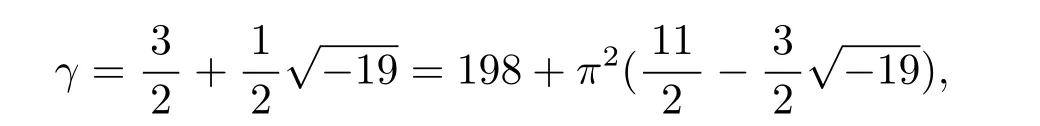
which implies that γ belongs to the class[198].

As an easy consequence of Theorem 2.1(5),we have

Corollary 2.5 Suppose that 2 is prime in Rd.Letwhere 0 6 a,b 6 2n−1−1,a,b∈ Z.Then

(1) α =[1]if and only if a=2n−1k1+1,b=2n−1k2,where k1,k2∈ Z are of the same parity.

(2)If a=2nk1+1,b=2nk2,k1,k2∈Z,then α =[1].

Now,we determine the structure of unit groups of Rd/⟨ϑn⟩for an arbitrary prime ϑ of Rd.First of all,we consider the case ofForit is easy to show that α∈U(R)if and only if d-(a2−db2),if and only if d-a,if and only if D-a.Then the unit groups U()ofare as the follows:

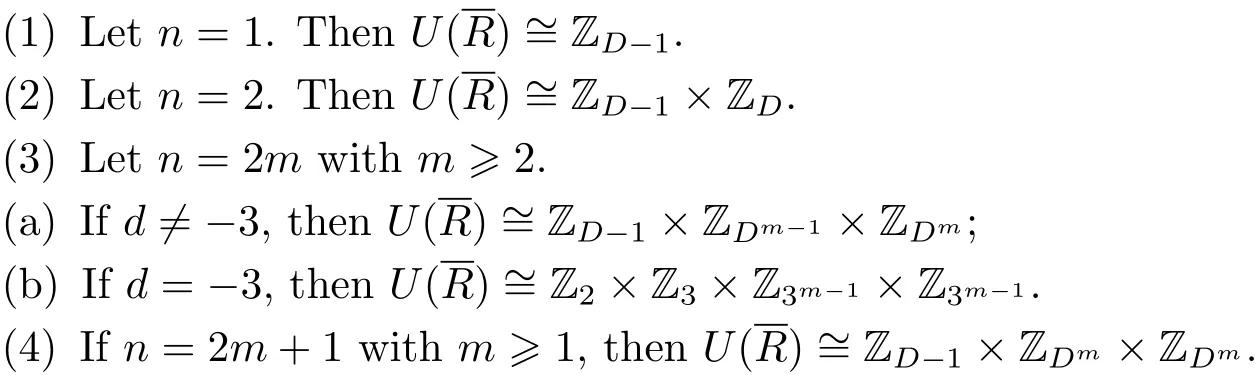
Proof(1)If n=1,by Theorem 2.1(2),is a field of order D=−d,so|U(R)|=D−1.Therefore,U()is a cyclic group of order D−1 and hence U()≌ZD−1.

On the other hand,if D=19,then D−1=2×32,clearly[4]∈U()is of order 32.If D=163,then D−1=2×34,clearly[4]∈U()is of order 34.Therefore H ≌ZD−1.So

(3)(a)Suppose that d ≠ −3.Let n=2m with m>2.Letwhere a,b ∈ {0,1,···,Dm− 1}.Since α ∈ U()if and only if D-a,|U()|=(D−1)D2m−1,and we can write U()=P×H,where P,H are finite groups,and|P|=D−1,|H|=D2m−1.

We determine the structure of H.Letwith D-a.By Theorem 2.1(1),for an arbitrary odd integer W>1,αWequals to the equivalence class[1],i.e.,αW=[1]if and only if the following congruences hold

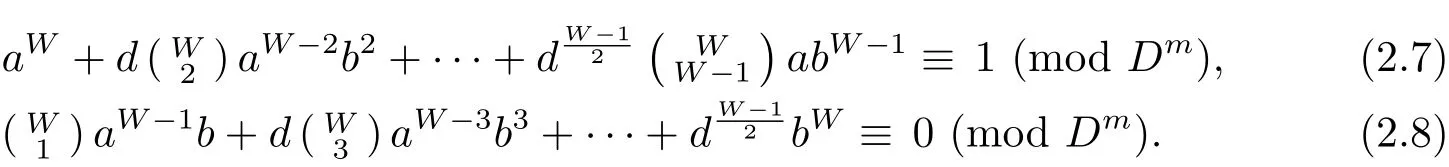
First,we claim that for any α ∈ H,αDm=[1].Let W=Dm.Sincefor j>1,the congruence(2.7)is equivalent to aDm≡1(mod Dm).It is well known that the unit group of the ring Z/⟨Dm⟩is isomorphic to ZDm−1× ZD−1.Hence,we obtain that aDm≡ 1(mod Dm)if and only if a ∈ ZDm−1.So in the set{0,1,···,Dm− 1},there are precisely Dm−1elements a such that

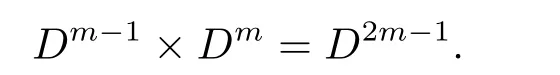
Second,we consider the number of α ∈U(R)satisfying αDm−1=[1].Let W=Dm−1.Sincefor j>1,congruence(2.7)holds if and only if aDm−1≡ 1(mod Dm),if and only if a∈ ZDm−1.

On the other hand,note that d ≠ −3 andforcongruence(2.8)is equivalent to Dm−1aDm−1−1b ≡ 0(mod Dm).That is,Dm−1b ≡ 0(mod Dm),since D-a.Hence,we obtain d|b.So the solutions to congruence(2.8)are b=D·l with l=0,1,···,Dm−1− 1.Thus the number ofsatisfying αDm−1=[1]is Dm−1×Dm−1=D2m−2.Then the number of elements of order Dmin U()is

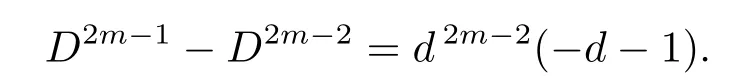
Finally,let we calculate the number of α ∈ H satisfying αDm−2≡ 1(mod Dm).Let W=Dm−2.Sincefor,congruence(2.8)holds if and only if

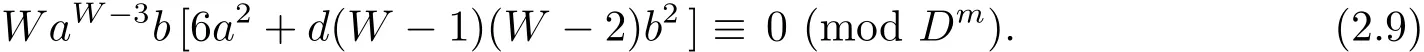
Since D-a and d≠−3,we derive that D-[6a2+d(W −1)(W −2)b2].So congruence(2.9)holds if and only if d2|b,i.e.,congruence(2.8)holds if and only if d2|b.Furthermore,in the case of d2|b,we havefor j>1.Hence,in the case of d2|b congruence(2.7)holds if and only if aW≡1(mod Dm).Clearly,the number of solutions of the last congruence is Dm−2.Thus the number of α ∈ H such that αDm−2=1 is Dm−2× Dm−2=d2m−4.So we derive that the number of elements of order Dm−1inis

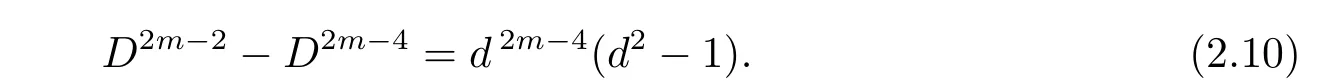
In the following,we determine the structure of the subgroup P of,where|P|=−d−1.Clearly,−d−1 is square-free for d= −7,−11,−43,−67 and hence P ≌ZD−1in these cases.If d=−19,then|P|=18=2×32.

On the other hand,let a<19mbe a positive integer.If a19t≡1(mod 19m)for some integers t>1,then clearly a=1+19x for some non-negative integers x.Hence,419t1(mod 19m)and(43)19t1(mod 19m)for any t>1.Furthermore,we have

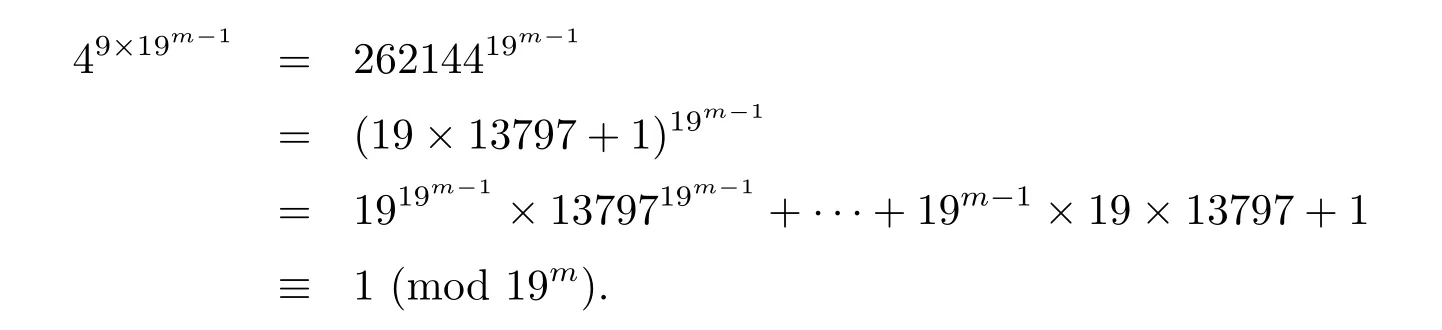
Thus,if d= −19,the class[4]∈is of order 32·19m−1,so P ≌Z2×Z32≌Z18.Analogously,if d=−163,we have

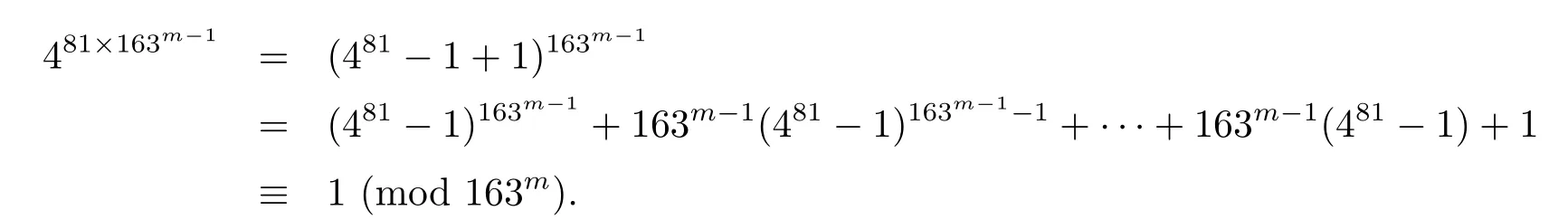
Since 163∥(481−1),the element[4]∈in the case of d= −163 is of order 34×163m−1,so P ≌Z2× Z34≌Z162. Therefore,we can conclude that P ≌ZD−1for d= −7,−11,−19,−43,−67,−163.Accordingly,as desired.

(b)Suppose that d= −3,n=2m,m>1.Letwhere a,b∈ {0,1,···,3m− 1}and 3-a.Since=2×32m−1,we can writewhere|Q|=32m−1.We claim that α3m−1=[1]for α ∈ Q.Let W=3m−1.Sincefor j>1,congruence(2.7)holds if and only if a3m−1≡ 1(mod 3m),if and only if a ∈ Z3m−1.

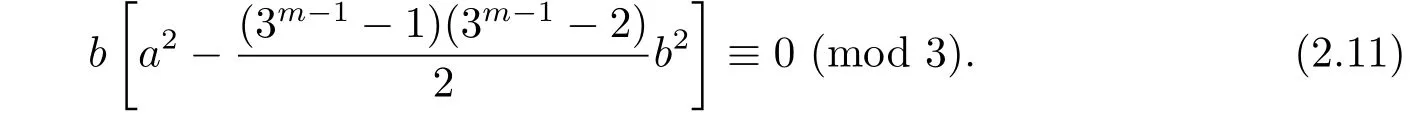
If 3|b,then clearly congruence(2.11)holds.If 3-b,we show that congruence(2.11)holds,too.Indeed,since 3-b,it follows from congruence(2.11)that

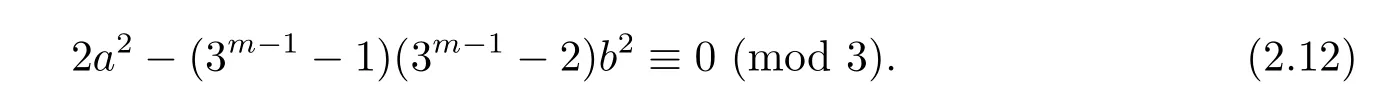
Moreover,we have 2a2≡2(mod 3)for 3-a.Thus congruence(2.12)reduces to 2−2b2≡0(mod 3).The last congruence holds for 3-b.Hence,congruence(2.12)holds for any integers b.So we can conclude that α3m−1=[1]if and only if

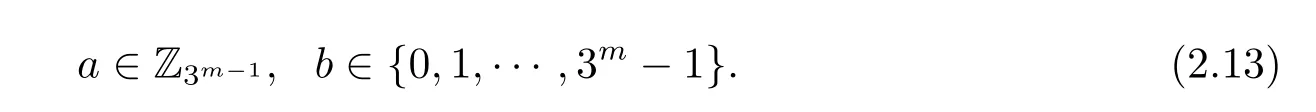
Thus there are precisely 3m−1× 3m=32m−1elements α ∈ U(R)such that α3m−1=[1].Recall that|Q|=32m−1,we obtain α3m−1=[1]for α ∈ Q.

Next,we show that there exist elements in Q with order 3m−1.Indeed,putting W=3m−2.Substituting the value for W into congruence(2.7).Note thatfor j>2,we derive that congruence(2.7)holds if and only if

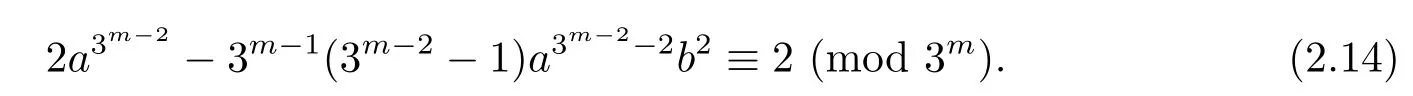
If we substitute a=b=1 into congruence(2.14),we have 3m−1(3m−2−1)≡ 0(mod 3m),which is impossible for m>2.Accordingly,congruence(2.7)does not hold for a=b=1,which implies thatMoreover,by the condition(2.13),[1].SoHence β is of order 3m−1.SoThus Q ≌Z3m−1× J,where J is a subgroup of Q with order 3m.

Now,we claim that there are elements in J with order 3m−1.We first note that(1+thusMoreover,sincewe conclude thatwhere 3-y and 3-s.LetBy condition(2.13),γ ∈ Q.Thus γ3m−1=[1]butHence,γ ∈ J.Substituting a=1,b=3 and W=3m−2into congruence(2.8),and note thatfor j>2,we derive that congruence(2.8)holds if and only if

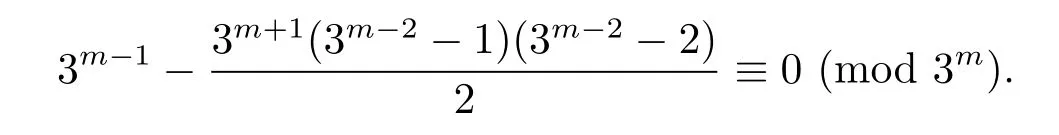
The above congruence does not hold for m>2.It follows that[1].Thus,γ ∈ J is of order 3m−1.Hence,Z3m−1is a subgroup of J,and J ≌Z3m−1× Z3.Accordingly,if d=−3,thenas desired.

(4)(a)Suppose that d ≠ −3.Let n=2m+1 with m>1.Forwe know thatif and only if D-a.Then,for n=2m+1,we have·D2m.Sowhere K,G are finite groups,and|K|=D−1,|G|=D2m.

We now determine the structure of G.Consider the polynomial expansions of αX,where X is an arbitrary integer.By Theorem 2.1(2),αXequals to the equivalence class[1]if and only if the following congruences hold

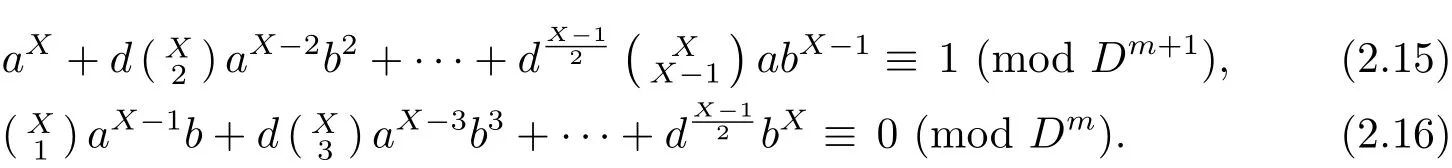
Firstly,putting X=Dm,and noting thatfor j>1,we derive that congruence(2.15)holds if and only if aDm≡ 1(mod Dm+1),if and only if a ∈ {1,2,···,Dm+1−1}with a∈ZDm.Therefore,congruence aDm≡1(mod Dm+1)has precisely Dmsolutions.

On the other hand,congruence(2.16)holds for b ∈ {1,2,···,Dm− 1}.Hence,the number of elements in U()satisfying αDm=[1]is Dm×Dm=D2m.Recall that|G|=D2m,we derive that αDm=[1]if and only if α ∈ G.

Secondly,substituting X=Dm−1into congruence(2.16).If αDm−1=[1],clearly α ∈ G.Since d ≠ −3,we havefor j>1.Therefore,congruence(2.16)holds if and only if D|b.In the case of D|b,congruence(2.15)holds if and only aDm−1≡ 1(mod Dm+1),if and only if a ∈ ZDm−1.Therefore,the number of elements in G satisfying αDm−1=[1]is Dm−1×Dm−1=D2m−2.Hence,there are precisely

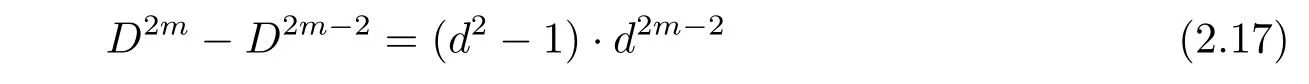
elements of order Dmin.

Suppose G2≌ZDs1×···×ZDsh,where s1+···+sh=m.If h>2,then 1 6 sj6 m−1 for j=1,···,h.Hence,there are precisely(D−1)·D2m−1elements of order Dmin,which contradicts the above result(2.17).If h=1,then G2≌ZDmand hence G ≌ZDm× ZDm.Thus the number of elements inof order Dmis(d2− 1)·d2m−2,which is the same as(2.17).Hence,we conclude that h=1 and G2≌ZDm.Therefore,if n=2m+1 with m>1,then U()≌K×ZDm×ZDm.

Finally,we determine the structure of the subgroup K for each case.Recall that|K|=D − 1.If d= −7,then|K|=6=2 × 3,we have K ≌Z2× Z3≌ZD−1.If d= −11,then|K|=10=2 × 5,thus K ≌Z2× Z5≌ZD−1.If d= −19,then|K|=18=2 × 32,and by the similar argument to(3)above,the element[4]∈is of order 32×19m.So K ≌Z2× Z32≌ZD−1.If d= −43,then|K|=42=6 × 7,so K ≌Z6× Z7≌ZD−1.If d= −67,then|K|=66=6 × 11,thus K ≌Z6× Z11≌ZD−1.If d= −163,then|K|=162=2×34,and by the similar argument to(3)above,the element[4]∈is of order 34× 163m.So K ≌Z2× Z34≌ZD−1.Hence K ≌ZD−1for each case.Thusas desired.

Now,substituting X=3m−1into congruence(2.16).We obtain that congruence(2.16)holds if and only if 2a2b−(3m−1−1)(3m−1−2)b3≡ 0(mod 3).We can verify that the last congruence holds for any integers b.

On the other hand,congruence(2.15)holds if and only if

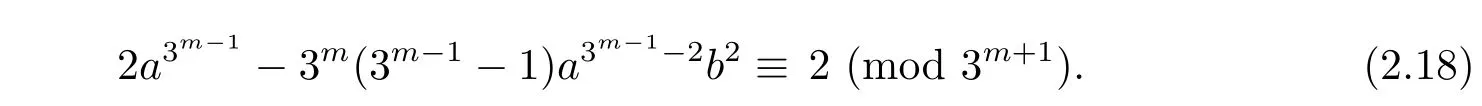
Clearly,the above congruence(2.18)does not hold,if a=b=1.So=[1],but.Hence,∈ G is of order 3m.Then G ≌Z3m ×E,where

Furthermore,if we substitute a=2,b=3 into above congruence(2.18),we have

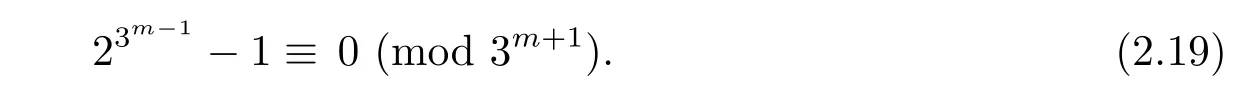
However,

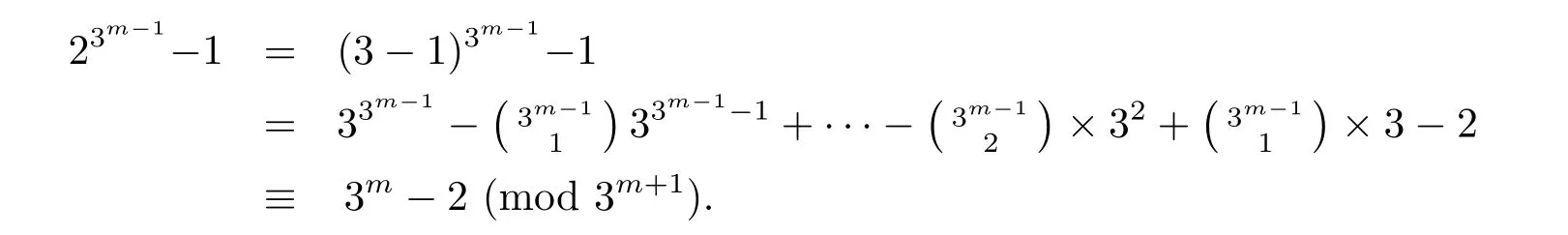
Therefore,congruence(2.19)does not hold for m>1.Hence,if we letthen by the above argument,we have γ3m=[1],but γ3m−1≠[1].Thus, γ is of order 3m.It leads to γ ∈ G.Moreover,where 3-y and 3-s.So we get thatwhich implies that γ ∈ E.Recall that|E|=3m,therefore we have

Theorem 2.7 Let p∈Z be an odd prime satisfying the Legendre symbol()= −1.LetThen

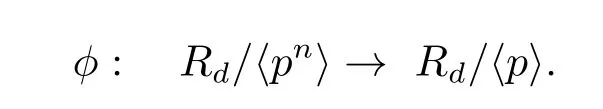
So there exists an epimorphism of groups

In the following,we investigate the structure of G2.ForIt is obvious that either p-a or p-b.Consider the polynomial expansions of αN,where N>1 is an arbitrary odd integer.It is evident that αN=[1]if and only if the following congruences hold

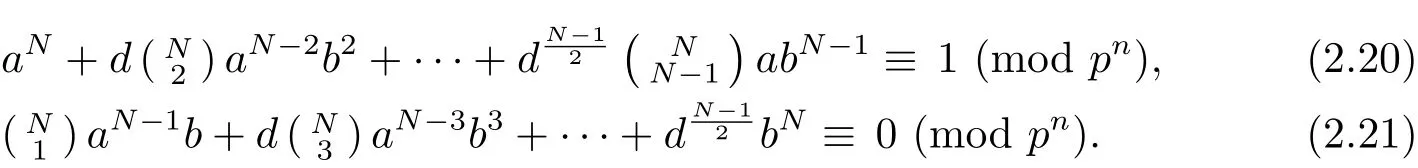
By the similar argument to Theorem 2.6(3),we know that αpn−1=1 for all α ∈ G2,and there are precisely p2n−4elements γ ∈ G2satisfying γpn−2=[1].

Suppose G2≌Zpn−1× Zph1× ···× Zphr,where h1+ ···+hr=n − 1.If r>2,then 1 6 hi6 n − 2 for i=1,···,r.Thus there are pn−2ph1···phr=p2n−3elements γ ∈ G2satisfying γpn−2=[1],which contradicts the above result.If r=1,then G2≌Zpn−1×Zpn−1.So there are exactly pn−2pn−2=p2n−4elements γ ∈ G2satisfying γpn−2=[1],which is the same as above result.So we derive that r=1 and this leads to G2≌Zpn−1× Zpn−1.This completes the proof.

Theorem 2.8 Let q∈Z be a prime satisfying the Legendre symbol()=1.Suppose that π is a proper factor of q.Let

ProofApplying Theorem 2.1(4),we derive that≌Z/⟨qn⟩.So the theorem follows.

We obtain from the proof of Theorem 1.2 that 2 is not a prime in Rdif d=−7.So we may assume d ≠ −7 in the following theorems.We investigate the unit groups of Rd/⟨2n⟩for d=−3,−11,−19,−43,−67,−163.

Theorem 2.9 Suppose d= −3,−11,−19,−43,−67,−163.Let=Rd/⟨2n⟩,n>2.Then

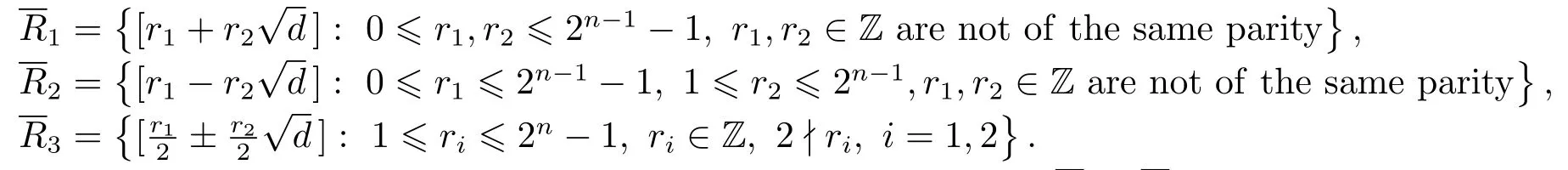
(2)Suppose n>4.Then there are exactly 8 elementssatisfying α2=[1].

(3)Suppose n>5.Then there are exactly 32 elementssatisfying α4=[1].

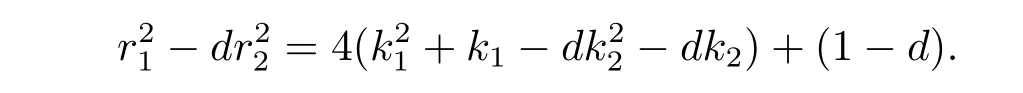
(2)First,let α =a ∈ Z,where 1 6 a 6 2n−1− 1.Thenif and only if 2-a.By Corollary 2.5,α2=[1]if and only if a2≡ 1(mod 2n).The last congruence has precisely 2 solutions.

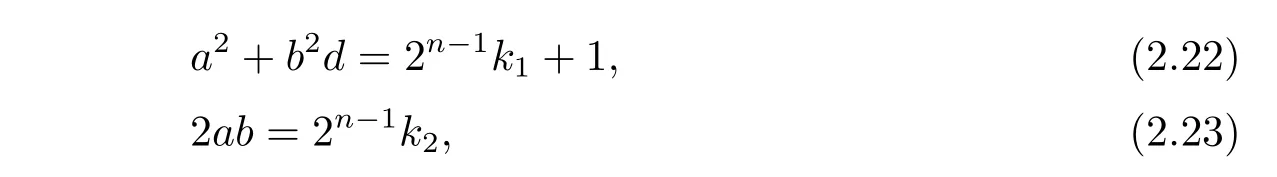
where k1and k2are of the same parity.If 2-a while 2|b,then(2.23)reduces to b≡0(mod 2n−2).Recall that 1 6 b 6 2n−1−1,so the last congruence has exactly one solution b=2n−2.Hence,the left hand of(2.23)is 2ab=2n−1a with 2-a.The left hand of(2.22)is a2+b2d=a2+22n−4d=a2+2n−1× 2n−3d.Because n>4,so 2n−3is even.Then equality(2.22)holds for some odd integers k1if and only if a2=2n−1k+1 for some odd integers k,if and only if a=2n−2± 1.So we can conclude that in the case of 2-a and 2|b,there are exactly 2 elements α satisfying α2=[1].

On the other hand,suppose that 2|a while 2-b.Then(2.23)reduces to a ≡ 0(mod 2n−2).Recall that 1 6 a 6 2n−1− 1,so the last congruence has exactly one solution a=2n−2.Hence,the left hand of(2.23)is 2ab=2n−1b with 2-b.The left hand of(2.22)is a2+b2d=22n−4+b2d=2n−1×2n−3+b2d.So equality(2.22)holds for some odd integers k1if and only if b2d=2n−1h+1 for some odd integers h.Putting b=2s+1,then b2d−1=4d(s2+s)+(d−1).Because s2+s is even and 4∥(d−1)for d= −3,−11,−19,−43,−67,−163,we obtain that 4 ∥(b2d − 1).Therefore,for n>4,b2d ≠2n−1h+1 for any integers h.So we can conclude that in the case of 2|a and 2-b,there does not exist any element α satisfying α2=[1].

On the other hand,if 2|a while 2-b,by the similar above argument,we obtain that α2≠[1].

Thus,there are exactly 8 elementssatisfying α2=[1],as desired.

(3)Firstly,let α =a ∈ Z,where 1 6 a 6 2n−1−1 with 2-a,a ∈ Z.By Corollary 2.5,α4=[1]if and only if a4≡ 1(mod 2n).The last congruence has precisely 4 solutions.

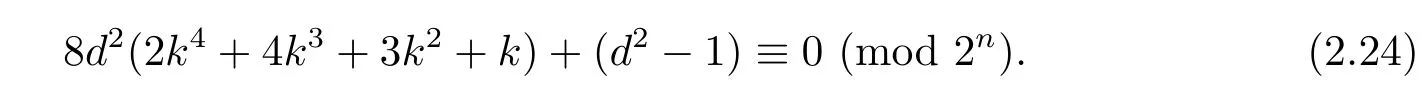
It is evident that 24-(d2−1)for d= −3,−11,−19,−43,−67,−163.So b4d2−10(mod 2n)for n>5.Thus,α4≠[1].

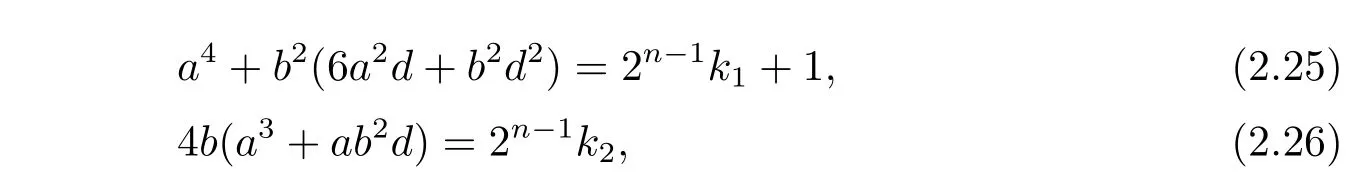
where k1and k2are of the same parity.If 2-a while 2|b,then(2.26)reduces to b≡0(mod 2n−3).The last congruence has exactly three solutions b=2n−3x,where x=1,2,3.Suppose first that b=2n−3x,x=1,3.Then the left hand of equation(2.26)equals 4b(a3+ab2d)=2n−1k2,where k2=x(a3+ab2d)is odd.

On the other hand,the left hand of equation(2.25)equals a4+2n−1(3 × 2n−4a2d+23n−11d2x2)x2.Since n>5,we get that(3 × 2n−4a2d+23n−11d2x2)x2is even.Therefore,α4=[1]if and only if a4=2n−1s+1 for some odd integers s.Since 1 6 a 6 2n−1− 1,clearly there are exactly 4 elements a satisfying a4=2n−1s+1 for some odd integers s.Now suppose b=2n−3x,where x=2.Then the left hand of equation(2.26)equals 4b(a3+ab2d)=2n(a3+ab2d).Therefore,by equation(2.25),we obtain that α4=[1]if and only if a4≡ 1(mod 2n).The last congruence has exactly 4 solutions a ∈ {1,···,2n−1−1}.Hence,there are totally 12 elements α satisfying α4=[1],in the case of 2-a and 2|b.For another case of 2|a and 2-b,we reduce from equation(2.25)that 2n−3|a.Hence,a=2n−3y,where y=1,2,3.Suppose a=2n−3y,where y=1,3.Then by equations(2.25)and(2.26),α4=[1]if and only if b4d2=2n−1s+1 for some odd integers s.Let b=2k+1,then b4d2−1 is equal to the left side of congruence(2.24).Since 24-(d2−1)for d= −3,−11,−19,−43,−67,−163.So b4d2− 10(mod 2n−1)for n>5.Thus,α4≠[1].Next,we assume that a=2n−3y,where y=2.Then by equations(2.25)and(2.26),α4=[1]if and only if b4d2≡1(mod 2n),if and only if congruence(2.24)holds for any integers k and n.However,this congruence does not hold for n>5.Therefore,we can conclude that in the case of 2|a and 2-b,there does not exist any element α satisfying α4=[1].Hence,there are totally 12 elementssatisfying α4=[1],where a ≠0 and b ≠0.

Thus,there are exactly 32 elementssatisfying α4=[1],as desired.

In the sequel,we assume that 2 is prime in the ring Rd.If n=1,by Theorem 2.1(5)and Theorem 2.9,Rd/⟨2⟩is a field with 4 elements.Therefore,U(Rd/⟨2n⟩) ≌Z3.

If n=2,then|U(Rd/⟨2n⟩)|=3 × 22.The unit group of Rd/⟨2n⟩is

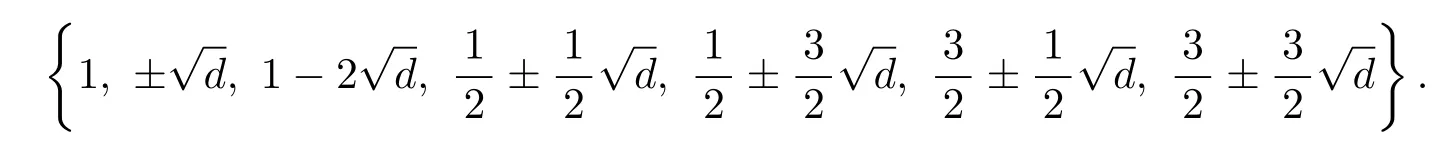
By calculation,we obtain that for,−11,−19,−43,−67,−163,=4k+1 for some integers k.So by Corollary 2.5,is of order 2.Similarly,=−27=[1].So the order ofis 3.Moreover,we show that=6.Hence,U(Rd/⟨22⟩) ≌Z3× Z2× Z2.

Analogously,if n=3,then|U(Rd/⟨2n⟩)|=3 × 24.The unit group of Rd/⟨2n⟩is

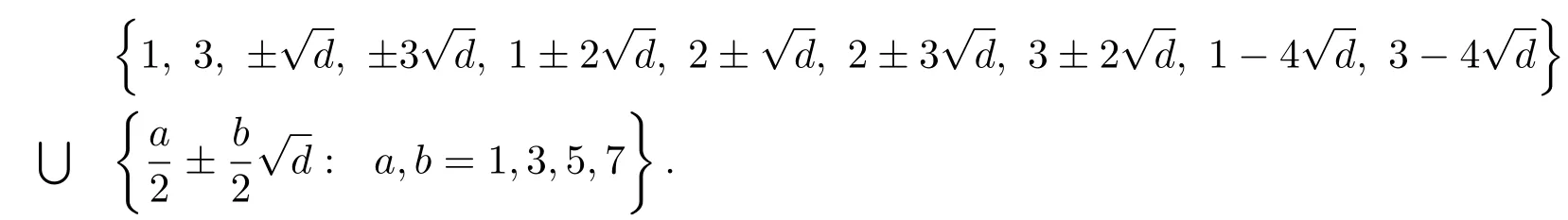
By calculation,we obtain thatandMoreover,4 for a,b=1,3,5,7.Therefore,U(Rd/⟨23⟩)≌Z3× Z22× Z2× Z2.

Theorem 2.10 Suppose that d=−3,−11,−19,−43,−67 or−163.Then

(1)U(Rd/⟨2⟩) ≌Z3.

(2)U(Rd/⟨2n⟩)≌Z3× Z2n−1× Z2n−2× Z2for n>2.

Proof The unit groups for the cases of n=1,2,3 have been stated above.So we assume n>4 in the following.By Theorem 2.9,we get|U(Rd/⟨2n⟩)|=3 × 22n−2.Thus U(Rd/⟨2n⟩)≌Z3× H,where H is a subgroup with order 22n−2.

Firstly,we claim that α2n−1=[1]for α ∈,whereandare stated in Theorem 2.9.Indeed,if we putαM=A+B,M is even,then

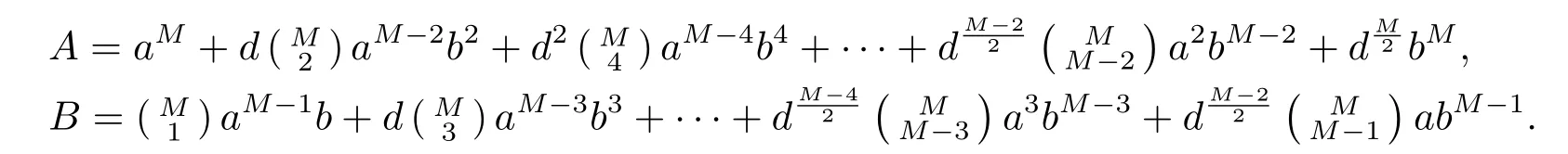
Let M=2n−1.If 2-a while 2|b,thenfor 1 6 s 6 2n−1.So we derive 2n|(A − a2n−1)and 2n|B.Hence,and B=2nk for some integers t,k.By Corollary 2.5,α2n−1=[1]if and only if a2n−1≡ 1(mod 2n).Because U(Z/⟨2n⟩) ≌Z2×Z2n−2for n>3,we derive that a2n−1≡ 1(mod 2n)for 2-a and n>3.Thus α2n−1=[1]in the case of 2-a and 2|b.

On the other hand,suppose 2|a while 2-b.Sincefor 0 6 s 6 2n−1− 1,it is obvious that 2n|(A − d2n−2b2n−1)and 2n|B.Since d,b ∈ U(Z/⟨2n⟩),we must have d2n−2≡ 1(mod 2n)and b2n−1≡ 1(mod 2n).Hence,d2n−2b2n−1≡ 1(mod 2n).Therefore, α2n−1=[1]in the case of 2|a and 2-b.So we conclude that α2n−1=[1]for α ∈.Similarly,we have α2n−1=[1]for α ∈.Thus,our claim follows.Secondly,we prove that Z2n−1is a subgroup of H.Since the number of the setR1∪R2 is precisely 22n−2and note that the subgroup H is of order 22n−2,we can conclude that α∈H if and only ifSoFurthermore,let α0=[2+ d]∈H.We prove that≠[1].Setting a=2,b=1,M=2n−2.Substituting these values into the expressions for A and B.Sincefor 3 6 s 6 2n−2,andfor s=1,2,we derive that 2n−1∥ (A − d2n−3)and 2n−1∥B.So A=2n−1k+d2n−3for some odd integers k.Moreover,owing to Corollary 2.5,=[1]if and only if A=2n−1t+1 for some odd integers t,i.e.,A=2n−1k+d2n−3=2n−1t+1,if and only if d2n−3=2n−1(t−k)+1.Since 2-kt,we have t− k is even.Therefore,=[1]if and only if d2n−3≡ 1(mod 2n).In the following,we show that d2n−31(mod 2n)for d= −3,−11,−19,−43,−67 or−163.Indeed,we have−d=4e−1 for some odd integers e.Then

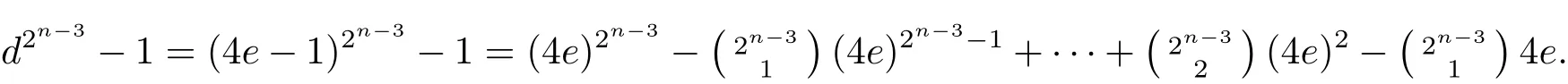
Now,owing to Theorem 2.9(2),we obtain that H ≌Z2n−1× Z2i× Z2j,where i,j>1 and i+j=n−1.If n=4,then i+j=3.Hence,H ≌Z2n−1×Z22×Z2for the case n=4.Next,we assume that n>4.If i,j>2,then there are precisely 64 elements α ∈ Z2n−1× Z2i× Z2jsatisfying α4=[1],which contradicts Theorem 2.9(3).If i=n − 2 and j=1,then there are precisely 32 elements α ∈ Z2n−1× Z2n−2× Z2satisfying α4=[1],which is the same as Theorem 2.9(3).Therefore,we conclude that H ≌Z2n−1×Z2n−2×Z2.This completes the proof of the theorem.