基于理性思维发展的高中数学课堂教学研究

☉江苏省常熟市梅李高级中学 孙 长

数学是一门逻辑性很强的理科.那么，我们如何在教学中渗透这个“理”呢？笔者认为在平时的教学中应该关注理性思维的发展.笔者曾有幸听了一节以理性思维发展为主线的数学公开课，下面结合具体的教学简录，谈一谈笔者的思考.

一、教学过程简录

1.知识准备

引题：已知集合A={x|x2-3x+2=0}和B={x|x-1=0}，判断A、B之间的关系.

学生：由A={1，2}，B={1}知，B是A的真子集.

2.学以致用

例1 已知集合A={x|x2-3x+2=0}与B={x|ax+1=0，x∈R}，若B⊆A，求实数a的值.

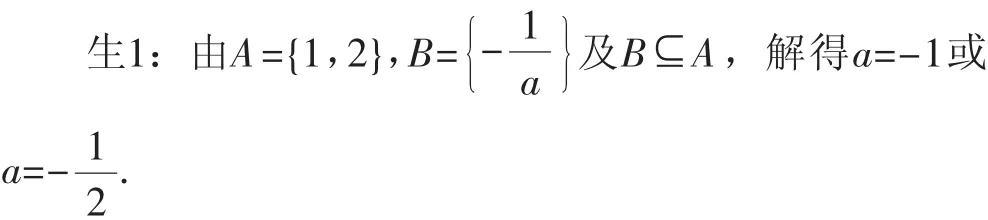
师：这是类比引题中的思路所作出的解题过程，生1首先用列举法表示了集合A、B，然后又结合B⊆A这一条件最终得出了a的值，方法看上去一点没有错误，但就是有一点问题，问题在哪里呢？

生2：a≠0……

很多学生产生疑惑：a≠0，但结果没有0呢……

师：a=0是一种特殊情况，大家想到用哪个方式可以判断呢？

生3：代入法.当a=0时，0·x+1=0没有实数解，即B=Ø，符合题意.

师（板书解题过程）：运用单个数值进行单独处理的思路很不错.那刚开始怎么会把a=0遗漏掉的呢？

生：解方程ax+1=0的时候将系数a除掉了.

师：很好.ax+1=0看上去像一次方程，事实上，当a≠0时，它是的；但是，当a=0时，它就不是了.因此，我们在解题时不能想当然地用除以a来求解.所以，我们解题时应进行理性的思考并准确把握研究对象的本质属性，轻易被某种形式迷惑后解题思路就会很容易产生偏差.

评注：质疑是学习者进行理性思考时最为突出的表现，因此，教师在教学中面对学生错误时不要简单修正，应该引导学生质疑并及时发现自己的思维缺陷，质疑、发现错误、自主修正的过程能够很好地培养学生的求真意识.其次，思考a=0是否可行并不能仅凭读题时的感觉来判断，运用代入检测这一数学方法进行确认的过程才是最求真务实的.

3.思维锻造

变式1：已知集合A={x|x2-3x+2=0}与B={x|x2-2x+2a-1=0，x∈R}，若B⊆A，求实数a的值.

生1：A={1，2}，

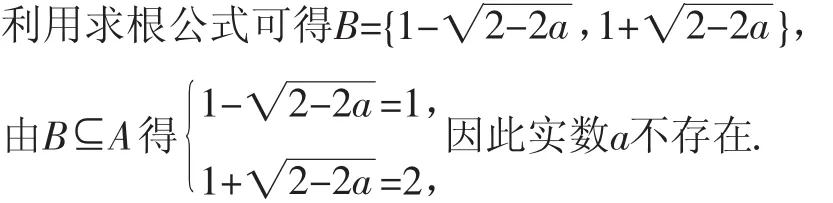
师：此题无解，同学们有意见吗？

生2：不对，有解的.

由题意可知，B=Ø，{1}，{2}，{1，2}. 当B=Ø时，Δ=4-8a+4＜0，即a＞1；当B={1}时，由根与系数的关系可得2a-1=1，即a=1；当B={2}时，实数a不存在；当B={1，2}时，实数a不存在.因此，a≥1.

师：分情况讨论并逐一验证讨论猜想才是最有依据、最可靠的，大家体会到利用求根公式求解的错误了吗？

生：求根公式在Δ＜0时不能用.师：当Δ＜0时，B=Ø，即a＞1；

师：很好.大家再看此题：已知一个含有n个元素的集合有2n个子集，如果我们将条件中的“集合A={x|x2-3x+2=0}”改成“集合A={1，2，3}”，那么集合B又有多少种可能呢？

生（个别）：8种，7种.

生（笑）：有很多.

师：子集的数量会随着元素的增多而“猛增”，因此进行逐一讨论自然是不够现实可行的，那么大家可有更好的方法来减少讨论的情况呢？回顾例1，能根据“A={1，2}，B⊆A”这一条件来断定集合B中元素的大概取值吗？

生：只能取到1、2.

师：很好，也就是说B=Ø或1∈B或2∈B，这样能解得结果吗？

生3：当B=Ø时，Δ=4-8a+4＜0，

即a＞1；当1∈B时，2a-2=0，

即a=1，此时B={1}⊆A；当2∈B时，2a-1=0，

综上所述，a≥1.

师：很好，根据这一解题思路来考虑，集合A中元素再多也没有关系.

评注：引导学生探求各种办法来解题的过程将求真、求简、求新的数学精神完全展现了出来.学生利用求根公式求解实数根时展现了其思维的片面性而导致结果产生错误，教师引导学生质疑与剖析错误的过程是促使学生逐步体验求真务实精神的渗透教学.教师在学生正确解题之后又及时引导学生换角度思考问题并获得更加简洁而新颖的解法，学生的研究意识、求简求新的理性精神在这一过程中也就得到了很好的培养与锻炼.

练习：已知集合A={x|x2-3x+2=0}与B={x|x2-2ax+2a-1=0，x∈R}，若B⊆A，求实数a的值.

生1：A={1，2}，当B=Ø时，

Δ=4a2-8a+4=4（a-1）2＜0，无解；

当1∈B时，1-2a+2a-1=0恒成立，

即a∈R；

当2∈R时，4-4a+2a-1=0，

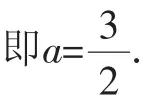
综上所述，a∈R.

师：“a∈R”这一条件告诉我们所有的实数a都是满足题意的，大家以为呢？

生2：a=0就不行.

师：能够找到反例就说明解题肯定有问题，那么问题究竟出在哪里了呢？

生3：x2-2ax+2a-1=0能因式分解，两根为x=1，x=2a-1，B={1，2a-1}.因此a=1或

评注：在学生初步掌握本类问题解题方法之际及时布置练习能够很好地帮助学生巩固、辨析知识，这也正是数学学习理性精神应该展现的地方.学生在巩固练习中也明白了数学问题的解决常常有通法与特法的存在，学生在实际问题的解决中应根据题意进行灵活的选择，“解无定法”的理性精神也在这一过程中得到了有意义的渗透.

4.沉淀结晶

变式2：已知集合A={x|x2-3x+2=0}与B={x|x2-2ax+m=0，x∈R}，如果B≠Ø且B⊆A，求实数a，m的值.

生1：A={1，2}，当1∈B时，1-2a+m=0；当2∈B时，4-4a+m=0.（再往后就解不下去了）

师：这一解题思路是存在着一定的道理的，那么联立方程组又代表了怎样的含义呢？

生：方程联立表示1∈B和2∈B是同时成立的.

师：是不是只有B={1，2}呢？

生：不是.

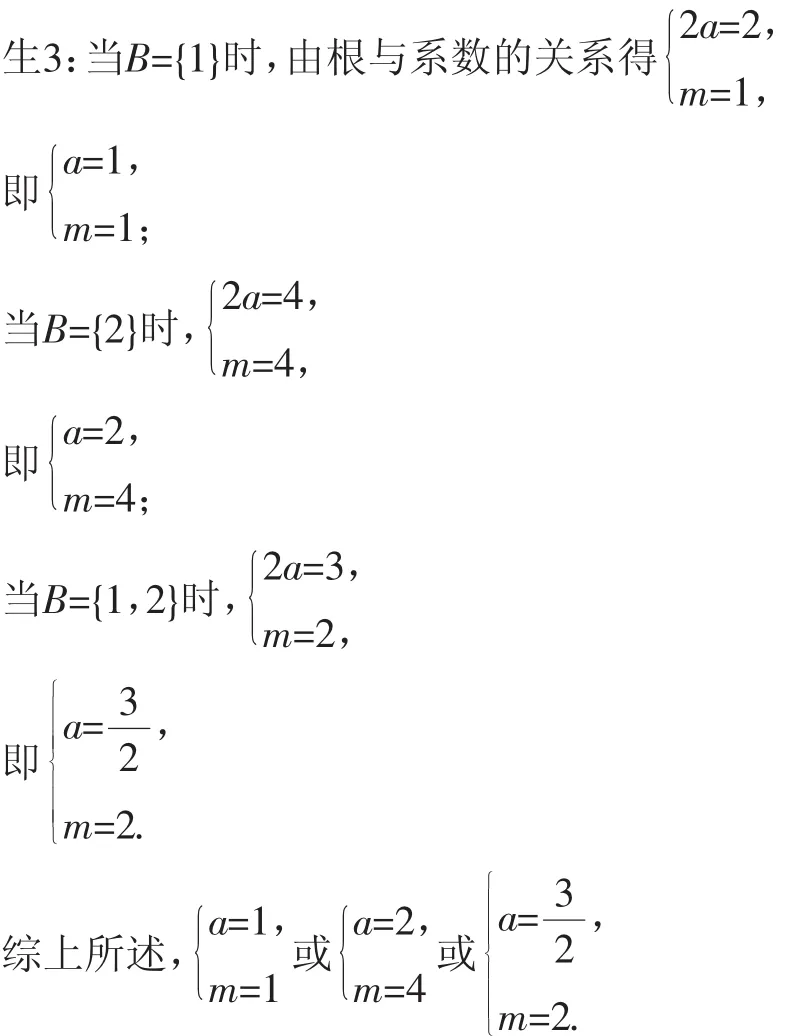
师：很好，变式1中的第二种解题方法在这里又得到了很好的运用，这可真是峰回路转啊.

最后教师再引导学生从上述集合的包含关系的问题中进行思考与总结，最终得出解决此类问题的基本思路.

评注：含有两个字母参数的一元二次方程的求解比之前的题目相对更有难度，学生从集合B的元素角度对问题展开思考并得到了一个无法求解的二元一次方程，这时候看上去已经无法继续解题，联立二元一次方程组成了唯一可以继续的路，最终得到a，m的一组数值，这充分表现出高一新生经常凭感觉做运算而欠缺理性精神.

二、笔者的些许思考

事实上，刚刚步入高中的学生最不能适应的往往就是数学的学习，导致高一学生数学学习不适应的原因有很多，其中最为重要的两个因素为：①高一学生尚未建立高中数学学习的良好思维方式与学习习惯，对于高一数学所涉及的解题策略、表达格式与能力目标等各方面内容也知之甚少；②集合知识的高度抽象性令学生在数学学习中时常感觉困难重重.

以集合的包含关系为载体的本课教学强调了集合的两种表示方式，列举法与描述法这两种表示方式之间的转化使得数学对象具体和抽象的特征得到了清晰的刻画和体现，辩证的思想也得到了很好的渗透；元素和集合的关系在解题的过程中得到了灵活的运用，个体和整体的意识也在解题的过程中得以渗透；由易到难的集合包含关系的变式将数学研究求真、求新的过程展现得淋漓尽致.学生自主学习的习惯与理性思维的方式都在这样的教学过程中得到了有意义的培养，不仅如此，学生对最优解题策略的探索、解题与表达格式的规范等环节也都能在这样的教学中一一达成.

由此可见，高中学生在数学学习中理性精神的培养具有可操作性，教师在实际教学中应理性选择、利用教学内容进行渗透理性精神的教学，理性教学策略与方法的合理运用一定能够保障数学教学的实在效果.