一题一世界
——一次说题的实践和思考

☉江苏省江安高级中学 黄建锋

说题是数学教研活动的一种重要载体，相比以往的解题，说题更为深刻地反映了对试题的理解、知识的运用，更为本质地思考以及深入研究后续考查点.可以这么说，说题形态渐渐成为各地教育主管部门考查教师的重要形式.如何说题呢？笔者以为从多个方面进行思考：首先，说解法；其次，说规律；最后，说思想和本质.

问题：非零向量a，b满足|a|=|b|=a·b=2，且（a-c）·（b-2c）=0，求|b-c|最小值.

一、说解法

本题是向量综合性问题，需要从综合性角度思考.试想，向量问题的主要入手方向是什么？根据向量的两要素——长度和方向，其入手方向自然是代数和几何.因此可以从不同的角度去探索基本解法.

解法1：不少学生对于向量的学习基本处在一维思维模式状态，即用“一维”数的眼光在看待“二维”向量的问题，因此其往往不可避免地陷入运算之中，即代数法的运用.不能说代数法不好，只是代数法在解决综合性问题时其优势相对较少.比如，学生往往喜欢这样解决：出发，利用（b-c）的构造，即0=（a-c）·

这是自由向量的构造，前提是整体性思想较为突出，并且对自由向量数量积运算有一定的要求.

解法2：不难发现，本题给出的两个向量满足夹角是60°，且模长已经给定，因此学生头脑中对其有更为简捷的代数方式——坐标向量，这是很多学生喜欢的向量求解方式.如图1，建立直角坐标系，设=c=（x，y），得a-c=（2-x，-y），b-2c=（1-2x，-2y），由（a-c）·（b-2c）=0，得（2-x）（1-2x）+（-y）（

图1

|b-c|2=.坐标法简单易操作，更注重向量代数性的工具，需要扎实的运算能力以及各种知识的综合性运用能力.

图2

解法3：从向量另一重要特性出发，其必有几何解法.对条件分析可知，向量a，b满足夹角60°，问题就围绕向量a，b，c建构图形解决.如图2，设a-c.由题意可知即∠ACD=90°，则点C的轨迹是以Q为圆心，以AD为直径的圆上的点.又|b-c|=||，问题转化为定点B与圆上动点C的最值.至此，问题已到达学生能认知的模式，|b-c|最小值为BQ-r.给出计从图形结构的角度入手，显然是对向量条件的图形化构造，这里垂直关系往往要结合平面几何中圆的相关知识，利用向量几何特征解决问题更有思维意义，也是考试命题的重要方向.

二、说规律

近年来，向量在中学数学中的地位愈来愈重要，向量问题的考查难度也在逐步加深，学生对向量的理解、教师对向量的教学难度也在不断上升，因此要通过问题将向量教学呈现出一定的规律性，从而获得向量教学更好的方式.

从向量在中学数学中的内容来看，其知识点主要呈现在：向量的概念—向量的加减法—向量的数乘—向量基本定理—数量积.在学习过程中呈现规律性的始终是两点：代数的运算方式或者几何图形的建构方式.这两点既是问题的本质所在，又体现了向量工具性的特征.从几何图形的角度来说，向量教学的规律主要是挖掘平面几何的意义，这也是问题解决的关键，将平面几何与向量几何特征紧密联系起来，问题的解决便是水到渠成的事.

变式1：非零向量a≠e，|e|=1，对任意t∈R，恒有|ate|≥|a-e|，则e·（a-e）=______.

图3

规律：从几何角度来说，这样的问题往往涉及平面几何中最基本的一个知识——“点到直线的距离垂线段最短”，若没有结合图形思考，学生往往通过代数的大量运算求解.从图3来看，不难发现垂线段最短这一几何规律，显然e⊥（a-e），因此数量积为0.类似的问题数不胜数.如果从代数规律中寻找，势必离不开一定的运算：由|a-te|≥|a-e|，两边平方，得t2-2（a·e）t+2a·e-1≥0，对任意t∈R恒成立，只要Δ=4（a·e）2-4（2a·e-1）≤0即可，所以Δ=4（a·e）2-4（2a·e-1）=4［（a·e）2-2a·e+1）］=4［（a·e-1）2］≤0，得（a·e-1）2≤0⇒a·e=1，显然此时的e·（a-e）=e·a-e2=0.

变式2： 设e1，e2为单位向量，非零向量b=xe1+ye2，x，

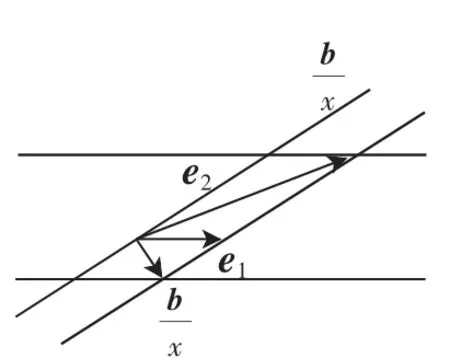
图4

规律：将问题稍加改变，思考“点到直线的距离垂线段最短”如何运用.不妨设x≠0，结合平行四边形法则（如图4），的最大值为2.问题依旧在寻找几何规律——垂线段最短，尽管有干扰元素x、y，但是其问题的规律性依旧，当然本题也可以从代数规律思考：b2=|b|2=（xe1+ye2）2=x2+y2+的最大值为2.

这里的两道变式题说的是问题的统一规律，即找到几何特征的规律，与本文中的原题相比，笔者认为几何特征的规律性更为重要一些，寻找问题的共性是说题的根本所在，也是近年来考试命题的方向所在，其比代数运算更重要.

三、说思想

向量问题解决的数学思想是什么？笔者以为主要是一个思想方法，即数形结合思想.数形结合思想在向量中的运用有两层含义，其一是以数解形，再者是以形辅数.向量试题恰恰是两方面的重要反映，紧紧抓住数形结合思想这两方面的立意，对于向量问题的解决有着重要作用.

图5

思路2：可以从＜a-c，b-c＞=60°及数量积出发，利用基本不等式求|c|的最值.由题意|a+b|=1，由（a-c）·（b-c）=结合上述两式：a·b-（a+b）·c+|c2|≤［1-（a+b）·c+|c|2］，化简，得|c|2≤2+（a+b）·c≤2+|a+b·||c|=2+|c|，得|c|2-|c|-2≤0⇒|c|≤2，即最大模长为2.

我们发现，向量问题的解决离不开数形结合思想，本文从问题开始到变式，以及改编，始终围绕数形结合思想的两条主线进行：以数如何解形？以形如何辅数？在说题过程中，至始至终围绕明确的数学思想将问题呈现出来，是说题的基本思想，另一方面我们要将向量问题的本质领会清楚：即向量问题的解法本质在于找到合适的图形建构或者是代数化的机械运算，这两大本质特性成为向量工具性最好的诠释.

说题是一个重要的教学形态，是教师不断优化问题解法的重要方式，笔者以为教师要提升自身综合素养、提升自身的解题水平，多参与这样的说题尝试，对于教师专业化的提升有重要的帮助.一个题就是多个知识点的整合，说好一个题，势必要厘清各种知识的内在联系以及整理解决问题的规律性的东西，摸索其背后的数学思想方法，甚至还能融会贯通的改编一些原创问题，长此以往就能获得“一个世界”，正所谓一题一世界，知识相连接.