电力系统暂态稳定紧急控制并行序贯优化算法

甘国晓，耿光超，仲悟之，江全元，徐振华，苏 毅，黄 霆

(1. 浙江大学 电气工程学院，浙江 杭州 310027；2. 中国电力科学研究院有限公司，北京 100192；3. 国网福建省电力有限公司电力科学研究院，福建 福州 350007)

0 引言

电力系统遭受严重扰动后，必须尽快采取控制措施保证系统的安全稳定运行。切机切负荷作为一种有效的暂态稳定紧急控制手段已得到广泛认可。然而，随着电力系统以及电力市场化的发展，电力系统紧急控制问题变得更加复杂。

目前，对于暂态稳定紧急控制问题的研究方法主要分为两大类：基于能量函数的直接法和基于最优控制理论的优化算法。直接法主要有基于稳定域边界的主导不稳定平衡点法[1]、暂态能量函数法[2]和扩展等面积法[3-4]等。它们都是构造一个稳定裕度，根据稳定裕度相对控制变量的灵敏度计算满足要求的控制策略。此类方法由于模型适应性较差，存在计算结果不准确的问题。基于最优控制理论的方法将紧急控制问题描述为包含微分代数方程(DAE)的最优控制问题[5]，采用动态优化算法求解。此类方法具有广泛的模型适应性，但存在求解效率不高的缺点。

求解动态优化问题的常用方法有联立法[6-8]和序贯类[9-11]的方法。联立法通过将DAE离散为非线性代数方程组，从而使动态优化问题转化为大规模非线性规划(NLP)问题，使用非线性优化方法直接求解。文献[7]和文献[8]将紧急控制问题建模为大规模NLP问题，分别基于并行简约空间内点法和伪普法进行求解，在一定程度上提升了求解效率。但随着系统规模的增大，“维数灾”的问题不可避免，计算速度仍然较慢。序贯类的方法则将DAE与优化问题分开求解。文献[9-10]基于约束转换，将最优切负荷问题分解为灵敏度计算和NLP问题的交替求解。文献[11]采用序贯法框架将动态优化问题分为模拟层和优化层，在模拟层基于正交配置求解DAE，但是灵敏度分析的计算量大，耗时较长。序贯法将DAE剥离原优化问题进行求解，虽然形成了较小规模的NLP问题，但同时也带来了DAE求解和灵敏度分析耗时过大的缺点，这在大规模系统的动态优化中尤为突出。

本文基于序贯法的框架将原问题分为仿真层和优化层进行交替求解。为提高仿真层的计算效率，基于有限元正交配置，并行求解DAE与灵敏度。在优化层采用预测校正内点法求解较小规模的NLP问题。不同方法的计算结果表明，有限元正交配置能以较少的离散点数获得较精确的结果，减少了计算量；并行计算技术加速了仿真层的计算过程；另外，由于不需要直接求解大规模NLP问题，本文方法比联立法的计算速度更快。

1 电力系统紧急控制数学模型

暂态稳定紧急控制问题可描述成一个含有DAE约束的动态优化问题，其一般形式为：

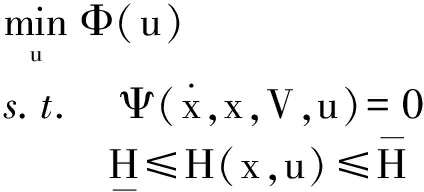
(1)

1.1 目标函数

为保持暂态稳定性，以切除最少的发电机和负荷为目标：

(2)

其中，u=[uGi,uL i]，uGi、uL i分别为各个发电机节点切机比例和负荷节点切负荷比例；rG、rL分别为可切发电机和可切负荷总数；aGi、aL i分别为切机、切负荷控制代价的权值；PGi、PL i分别为各可切发电机节点的容量和各可切负荷节点的总负荷量。

1.2 等式约束

a. 动态方程。

电力系统动态方程包含发电机转子运动方程、励磁系统与调速系统动态方程等，可以描述为：

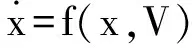
(3)

其中，x为包括发电机功角、角速度等在内的微分状态变量；V为包括节点电压等在内的代数变量。

b. 网络方程。

网络方程可以表示成如下形式：

(4)

其中，G、B分别为节点导纳矩阵的电导部分和电纳部分；Vx、Vy分别为节点电压实部和虚部；Ix、Iy分别为节点注入电流的实部和虚部。

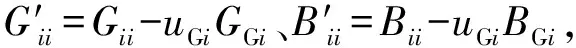
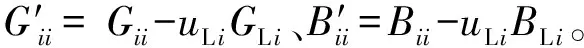
1.3 不等式约束

不等式约束包括暂态稳定约束和切机切负荷比例的上下限约束。本文采用各发电机功角与惯性中心角的偏差不超过指定角度作为暂态稳定约束：

(5)

其中，δi为第i台发电机功角；NG为发电机总数；δCOI为发电机功角的惯性中心，可由式(6)计算。

(6)

其中，TJi为第i台发电机的惯性时间常数。

切机切负荷上下限约束：

(7)

2 并行序贯优化算法

2.1 序贯优化算法

序贯法将原动态优化问题分为仿真和优化2个子问题交替迭代，构成一个序贯的求解过程，算法框架如图1所示。仿真子问题求解式(1)中的DAE初值问题：

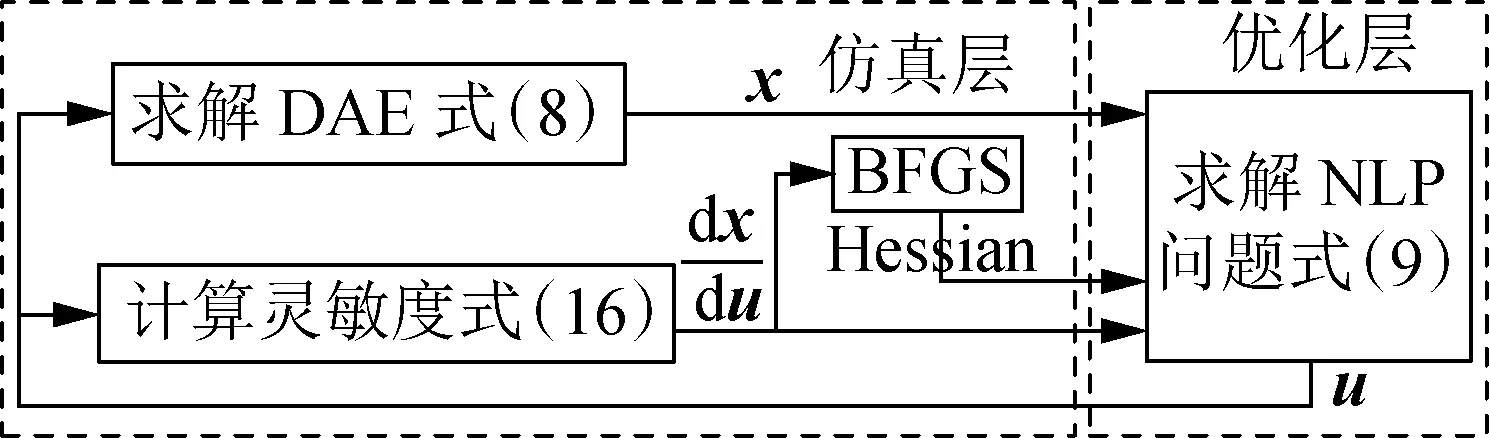
图1 本文算法框架Fig.1 Framework of proposed method

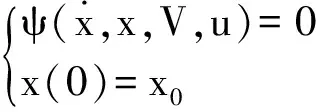
(8)

给定状态变量的初始值x0，在仿真层通过数值方法求解动态优化问题式(1)中的DAE约束Ψ，可以得到状态变量x在整个时域上的值。求解DAE的常用方法有改进欧拉法、隐式梯形积分等方法，在基于联立法[7]或者序贯法[12]的暂态稳定控制优化算法中，常用隐式梯形积分对微分方程进行离散化。隐式梯形积分求解DAE时采用较小的步长，计算量大。而有限元正交配置[11,13]具有离散点数少、计算精度高、稳定性好等优点，为了提高仿真层的计算效率，本文用其求解DAE。

在仿真层采用数值方法求出状态变量后，可以得到各个状态变量在各个离散时间点上的数值解，再将状态变量的不等式约束加于所有离散点上，可使过程约束H近似为状态变量在各个离散点处的约束。此时DAE等式约束已经被消除，状态变量x可以视为控制变量u的隐函数，仍需计算状态变量对控制变量的灵敏度信息。则原动态优化问题可以转化为一个较小规模的NLP问题：

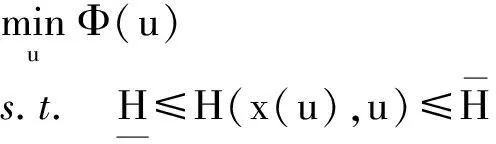
(9)

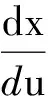
2.2 基于有限元正交配置的DAE求解

如图2所示，在时域t0～T上配置NL个有限元，每个有限元有NC+1个配置点。为保持状态变量的连续性，本文采用Radau 配置点法，即前一有限元的最后一个配置点等于后一有限元的起始配置点，以NC=3为例，如图2所示。式(3)中的微分变量x可近似为一组拉格朗日多项式的线性组合：

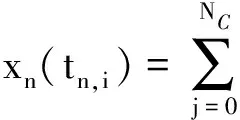
i=1,2，…,NC；n=1,2，…,NL

(10)

其中，xn(tn,i)为状态变量在第n个有限元的多项式近似；xn,j为状态变量在第n个有限元第j个配置点的值；lj(tn,i)为拉格朗日多项式；tn,i为第n个有限元的第i个配置点。

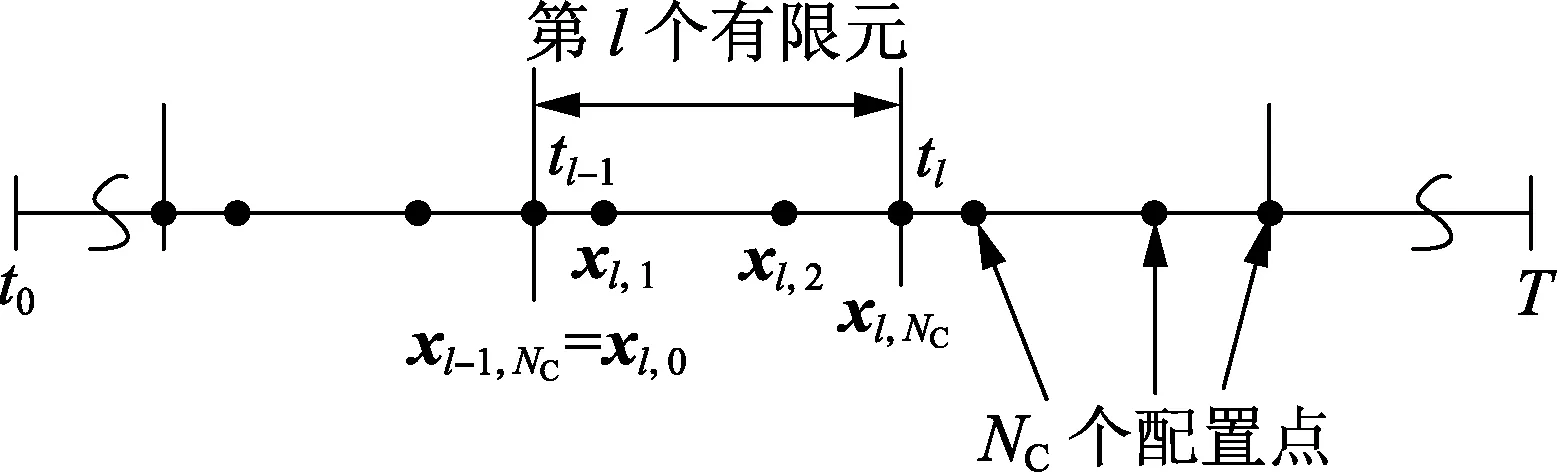
图2 Radau正交配置点Fig.2 Radau orthogonal collocation points

对式(10)的拉格朗日多项式求一阶导可得：

i=1,2，…,NC；n=1,2，…,NL

(11)

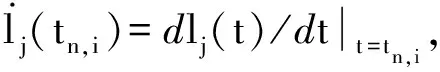
通过正交配置法，式(3)的微分方程可以转化为一系列的非线性代数方程：

i=1,2，…,NC；n=1,2，…,NL

(12)

求解上述非线性代数方程组即可得到状态变量在各个离散点处的值。本文采用非诚实牛顿法(VDHN)[14]求解正交配置离散后的DAE。

2.3 并行灵敏度计算

在第n个有限元，离散后的DAE可以表示为：

(13)

其中，Fn和gn分别为第n个有限元处离散后的动态方程和网络方程；xn为第n个有限元中NC个配置点上的状态变量；xn,0为第n个有限元中初始配置点的值；Vn为第n个有限元中NC个配置点上的代数变量。

为了求出各个离散点处状态变量对控制量的灵敏度，对式(13)采用链式求导法则可得：

(14)

定义Jn如下：

(15)

第n个有限元的灵敏度方程可以表示为：

(16)

由于采用Radau 配置点法，即前一有限元的最后一个配置点等于后一有限元的起始配置点，则有：

(17)

通过式(16)、(17)，状态变量对控制变量的灵敏度可以从一个有限元到下一个有限元顺序进行求解，这与DAE的求解顺序是一致的，因此可以将它们并行执行。值得注意的是，在求解第n个有限元处的DAE时，第k次牛顿迭代需要求解线性方程组：

(18)

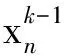
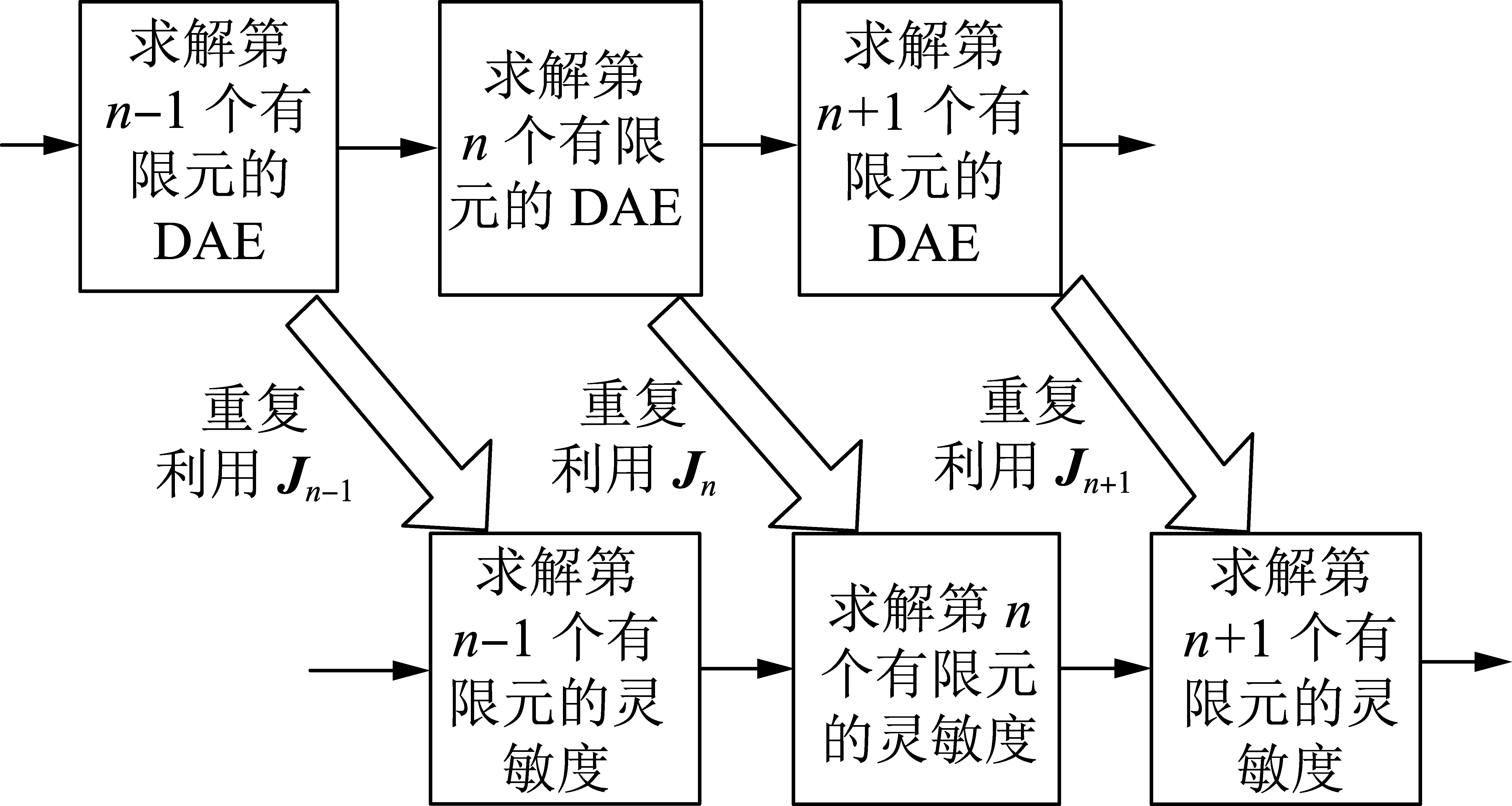
图3 仿真层框架Fig.3 Framework of simulation layer

另外，灵敏度方程式(16)是一个含多右边项的线性方程组，利用求解DAE时Jn的因式分解结果，只需进行前代回代过程即可得到第n个有限元处的灵敏度。由于多个右边项的前代回代过程相互独立，为了进一步提升效率，可以对不同右边项的回代过程采用多个计算核心并行执行，如图4所示。

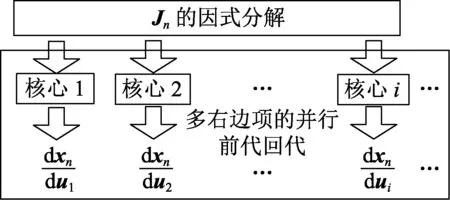
图4 并行灵敏度计算Fig.4 Parallel sensitivity calculation

计算出状态变量x对于控制变量u的灵敏度即可求出不等式约束对控制量的一阶梯度。不仅一阶梯度，二阶梯度对基于梯度的优化算法也至关重要。由于对控制变量的二阶导数难以用解析的方法获得，BFGS(Broyden-Fletcher-Goldfarb-Shanno)[15]方法被用于近似海森矩阵：

(19)

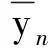
(20)

其中，un为第n次迭代的控制变量值；yn和ζn如式(21)所示。

(21)

其中，▽uΦn为第n次迭代时目标函数对控制量的一阶梯度；▽uHn为第n次迭代时不等式约束对控制量的一阶梯度；zH和wH为内点法中不等式约束对应的拉格朗日乘子。

3 算例分析

本文算法采用C++ 编程实现，测试环境为Intel Xeon E5-2650 2 GHz CPU，采用OpenMP[16]实现多线程并行。其中，仿真过程采用了KLU[17]解法器进行稀疏线性方程组的求解，优化过程调用了英特尔提供的高性能多线程线性代数库(MKL)进行稠密矩阵的运算。测试算例参数如表1所示，其中nB、nL、nG、nLoad分别为系统节点数、线路数、发电机数和负荷数。发电机考虑二阶经典模型，负荷采用恒定阻抗模型，对所有算例优化1.8 s，t=0时刻发生三相接地故障，t=0.2 s切除故障线路，t=0.3 s实施紧急控制措施。有限元个数NL=8，NC=3。暂态稳定约束中相对功角的上下限取为±110°。

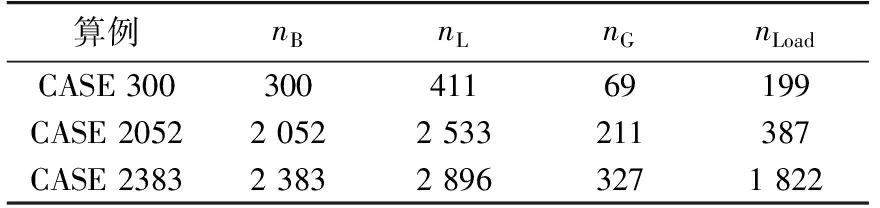
表1 测试算例Table 1 Test cases

3.1 计算结果比较

采用不同的方法对算例进行计算，结果对比如表2所示。对比方法为基于隐式梯形积分的并行序贯法，即在本文算法框架下，在求解DAE时，将有限元正交配置法换成隐式梯形积分，离散步长为0.01 s。从表2可以看出，2种方法的优化结果、迭代次数相差不大，但在同样采用并行计算的情况下本文方法耗时更少。与基于隐式梯形积分的并行序贯法对比，本文采用有限元正交配置法离散DAE，能够以较少的离散点数达到较好的计算精度，计算效率更高。

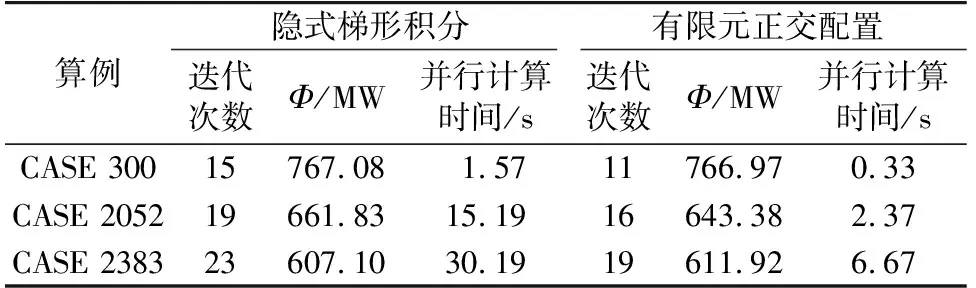
表2 计算结果比较Table 2 Comparison of calculation results

3.2 计算效率分析

表3给出了本文方法的各部分计算耗时，其中tCPU、tS、tO和PS分别为计算总耗时、仿真层耗时、优化层耗时和仿真层占总耗时的比值。从表3可以看出，仿真层的计算时间占了总时间的绝大部分，这是由于原动态优化问题的DAE约束已在仿真层计算，转化得到较小规模的NLP问题，所以优化层的求解耗时很少。另外，本文方法只需几秒钟的耗时即可得出解决方案，这得益于仿真与优化的分离，避免了直接求解大规模NLP问题，而且并行计算加速了仿真层的求解。

表3 计算时间Table 3 Calculation time

为了表征算法的并行效率，定义了灵敏度计算加速比和仿真层计算加速比。其中，灵敏度计算加速比为单线程灵敏度计算时间除以多线程灵敏度计算时间，仿真层计算加速比为单线程仿真层计算时间除以多线程仿真层计算时间。图5给出了在不同计算线程数下灵敏度计算过程的加速比。由图5可以看出，灵敏度计算的过程几乎可以达到线性加速比，加速效果明显。图6则给出了整个仿真层的加速比，随着线程数的增加，加速比增长放缓，8线程时最大加速比达到4.8。通常，测试算例的规模越大，加速效果越好。因此，本文算法对大规模系统暂态稳定紧急控制问题的求解有较好的潜力。

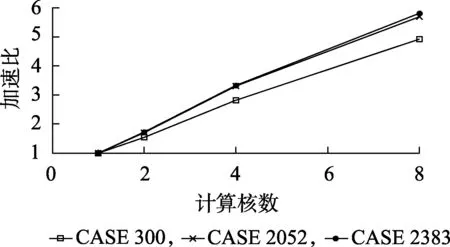
图5 灵敏度计算过程加速比Fig.5 Speedup ratio in process of sensitivity calculation

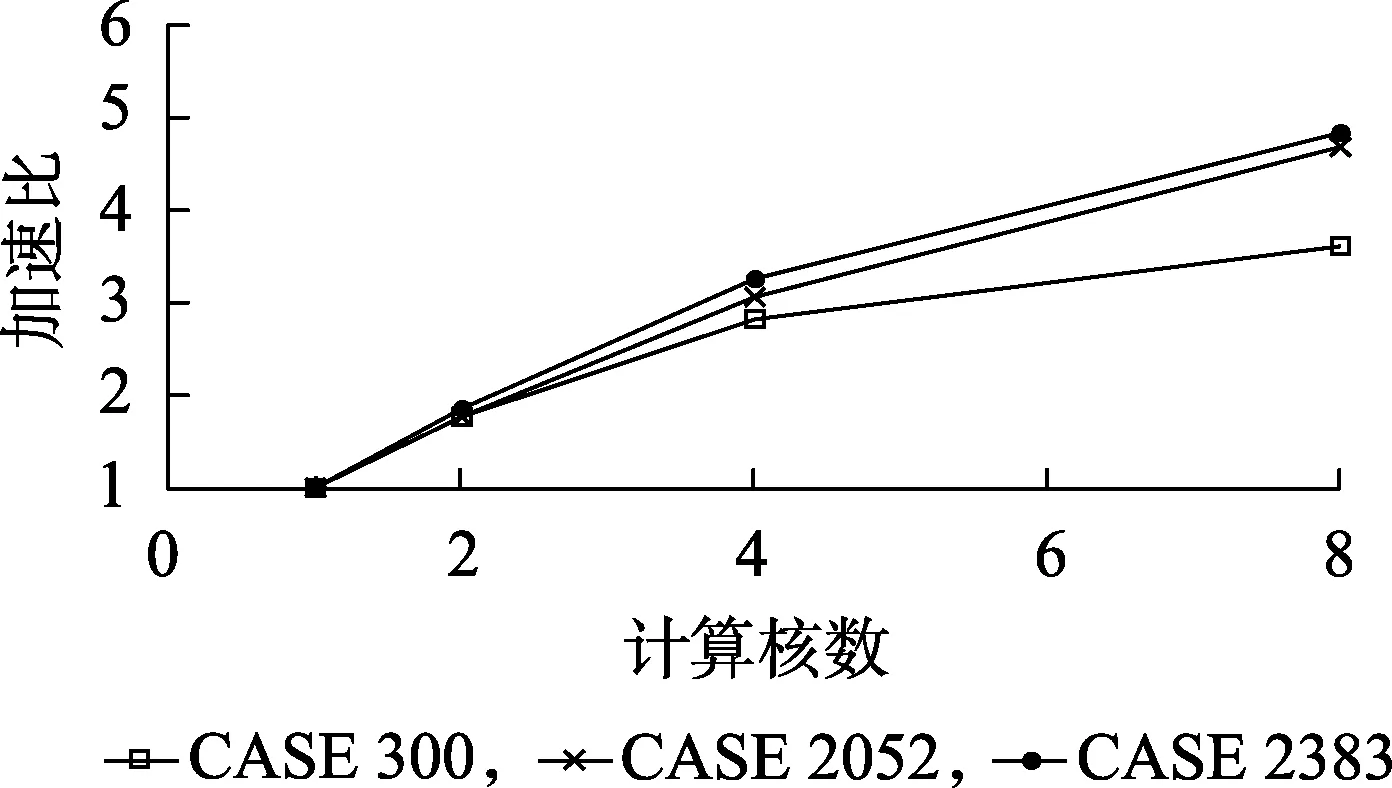
图6 仿真层加速比Fig.6 Speedup ratio in simulation layer

图7 算例仿真结果Fig.7 Simulative results of test cases

3.3 仿真验证

对算例进行时域仿真验证本文算法的有效性，各个算例的发电机功角曲线如图7所示。其中，虚线表示系统发生故障后没有紧急控制的功角曲线；实线表示执行切机切负荷操作的功角曲线。由图7可以看出，如果不执行紧急控制措施，电力系统发生故障后将失去稳定；采用本文算法的计算结果进行切机切负荷操作，系统的暂态稳定性得到明显改善。

4 结论

本文提出一种基于有限元正交配置的并行序贯法求解电力系统紧急控制问题。计算结果表明，相比隐式梯形积分，有限元正交配置能以较少的离散点数获得较精确的结果，减少了计算量；灵敏度计算过程重用DAE求解时的雅可比因式分解，并将这2个过程并行化，加速了仿真层的计算，提升了序贯优化算法的效率。另外，由于不需要直接求解大规模NLP问题，本文方法计算速度快，适合快速求解大规模系统的紧急控制问题。