PHM系统中的测试不确定优化选择建模

，， ，

(1.空军工程大学 装备管理与无人机工程学院，西安 710051； 2.空军工程大学 航空工程学院，西安 710038)

0 引言

预测与健康管理(PHM)是实现状态维修保障的关键技术，目前新研制军用飞机明确提出必须装备预测与健康管理系统。通过对某型军用飞机预测与健康管理系统的使用数据分析，系统针对飞机故障的提前预警与故障隔离定位精度较高，但系统发生虚警的概率非常严重，即在使用过程中，系统评估飞机的状态发生故障，但是经过拆卸故障组件进行内场测试检验后，发现组件正常。据某飞行基地的统计，某型飞机在试飞间发生的故障虚警率已占到总故障率的90%，这极大的影响了飞机的日常飞行保障工作。

为了解决这类问题，相关学者机构开展了以下研究。一是把系统中的不确定性因素当成随机变量，引入到状态评估模型中，然后采用相应滤波算法模型，将不确定性消除，文献[1-3]就是采用这种方法。作者在文献[4-5]中把测试不确定性概率和概率分布变量引入到状态预测评估模型中，然后采用贝叶斯滤波或粒子滤波的方法，降低不确定性的影响。这种方法存在两个问题：一是不确定性的先验概率和分布不容易确定，第二是作者将此方法应用到某型飞机的预测与健康管理系统评估模型中，在实际使用中并未显著降低系统虚警率。解决虚警率的另一种思路，是采用多种方法融合的方式[6-7]，但是这只能消除模型评估的不确定度，并且各个模型融合权重的确定，又带来状态评估的不确定性。

军用飞机预测与健康管理系统发生虚警的重要根源，是因为其工作在复杂的自然环境和电磁环境中，致使状态评估监测信号发生了偏移，造成测试的不确定性，测试的不确定性进入状态评估模型中，从而引起预测与健康管理系统的虚警[8]。因此，作者认为，要从根本上降低系统的虚警率，必须从预测与健康管理的根源解决，即在选择状态评估测试点时必须考虑信号测试的不确定性，从而优化预测与健康管理的状态评估策略，再结合相应的滤波方式和融合方法，这样才能有效降低系统虚警率。

目前国内外关于测试点优化选择的文献，大多不考虑测试的不确定性，只考虑故障覆盖率、隔离率、测试成本等因素的影响[9-12]。而考虑测试不可靠性的测试点选择模型中，相关研究将测试的不确定性看作随机变量，采用概率建模的方法对测试的不可靠度进行评估，并基于概率论对测试性优化选择进行研究[13-17]。然而使用传统概率论的前提是必须有充足的历史数据，使获得的概率分布充分接近实际概率。复杂环境下军用飞机测试不确定数据严重缺失，限制了传统概率论在不确定测试优化选择研究中的应用。这种情况下，只能利用专家的知识和经验来估计PHM中的测试不确定性，并给出专家信度。此时，若坚持使用概率论来处理专家信度，则可能导致错误决策。

本文基于满足自对偶、次可加的不确定理论研究PHM系统中的测试不可靠度，通过建立测试不确定条件下的测试优化选择模型，将不确定条件下的测试优化选择问题转化为不确定优化选择问题，并利用不确定变量和不确定分布，在期望值准则和乐观值准则下，将不确定优化选择模型，转化为带有专家信度的确定性优化选择模型，并通过实例给出了不确定优选选择模型的建模和求解过程。

1 不确定理论

定义1.1：(Liu[18])假设Γ是一个非空集合。L是Γ上的一个σ-代数。σ-代数L中的每一个元素Λ被称作一个事件。如果L到[0,1]的集函数M满足如下三条公理：

1)M{Γ}=1；

2)对任何事件Λ，成立M{Λ}+M{Λc}=1；

则称M为不确定测度，称三元组(Γ,L,M)为不确定空间。

定义1.2：(Liu[18])不确定变量ξ是从不确定空间(Γ,L,M)到实数集的一个可测函数，即：对实数上的任意Borel集B，有{ξ∈B}={y∈Γ|ξ(y)∈B}是一个事件。

定义1.3：(Liu[18])不确定变量ξ的分布函数Φ定义为：对任意实数x，

Φx=M{ξ≤x}

定义1.4：(Liu[18])如果，对任意α∈(0,1)，不确定分布Φ的逆函数Φ-1(α)存在且唯一，那么，我们称不确定分布Φ是正则的。

定义1.5：(Liu[18])设ξ1,ξ2,…，ξn是独立正则的不确定变量，对应的不确定分布函数分别为：Φ1,Φ2,…，Φn。如果f(x1,x2,…，xn)是一个关于x1,x2,…，xm严格递增，关xm+1,xm+2,…，xn于严格递减的严格单调函数，那么

ξ=f(ξ1,ξ2,…，ξn)

2 测试不确定优化选择模型

2.1 测试优化选择建模

1)有限的故障模式集，S={s1,s2,…,sm}，其中表示故障模式的总数目；

2)有限的可用测试集，T={t1,t2,…,tn}，其中表示测试的总数目；

3)测试相关矩阵，D=[dij]m×n，其中dij∈{0,1}，dij=0代表故障si发生时tj测试通过，dij=1故障si发生时tj测试不通过；

4)各个测试的成本，CP={CP1,CP2,…,CPn}；

5)测试选择向量，X=(x1,x2,…xn)T表示对应的测试是否被选择，即：xi=1代表ti被选择，xi=0代表ti未被选择；

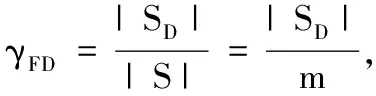
8)测试优化选择模型

2.2 测试不确定优化选择建模

在测试优化选择模型中，当某一故障si发生时，测试相关矩阵D=[dij]m×n中dij=0对应的测试tj肯定通过，对应的dij=1的测试tj肯定测试不通过。然而，实践证明，这一假设并不完全成立，在实际工作过程中，由于电磁干扰、不可靠传感器、非直接测量和环境变化等因素的影响，测试本身存在很大的不确定性，为此本文引入测试不确定度的概念。

1)测试不确定度ξ=(ξ1,ξ2,…ξn)，代表测试ti的测试不可靠程度，其中0≤ξi≤1，ξi=0代表测试完全可靠，ξi=1代表测试完全不可靠，我们假定其不确定分布为Φ(ξ)。

3)测试相关矩阵：在测试不可靠条件下，测试相关矩阵D=[dij(ξ)]m×n。测试不可靠条件下，对应dij=0时，故障si发生时tj测试不通过的不确定度为ξj，即：dij(ξ)=ξj；测试不可靠条件下，对应dij=1时，故障si发生时tj测试不通过的不确定度为1-ξj，即：dij(ξ)=1-ξj；综合可得：dij(ξ)=dij+(-1)dijξj

(3)故障检测率，在测试不可靠的情况下，故障检测率为测试在不可靠条件下故障检测数与故障模式总数的比值。

4)故障隔离率，在测试不可靠的情况下，故障隔离率为测试在不可靠条件下的故障隔离数与可检测故障数比值。

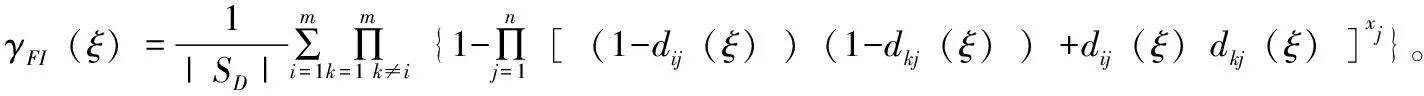
6)漏检率，为由于测试不可靠造成的故障漏检数与可检测故障数的比值。

7)测试不确定优化选择模型

约束条件：

3 测试不确定优化选择模型求解

3.1 不确定目标函数求解

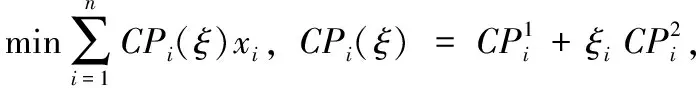
3.2 不确定约束条件求解

[定义3.1]集合Ai={j|dij=1}(i=1,2,…,m)，集合Bi={j|dij=0}(i=1,2,…,m)

Ak={j|dkj=1}(k=1,2,…,m,k≠i)，集合Bk={j|dkj=0}(k=1,2,…,m,k≠i)

对于j∈Ai，dij(ξ)=dij+(-1)dijξj=1-ξj

对于j∈Bi，dij(ξ)=dij+(-1)dijξj=ξj

1)检测率不确定约束条件求解

在乐观值准则下：

2)隔离率不确定约束条件求解

对于j∈Ai∩Ak，dij(ξ)=dij+(-1)dijξj=1-ξj，dkj(ξ)=dkj+(-1)dkjξj=1-ξj

对于j∈Ai∩Bk，dij(ξ)=dij+(-1)dijξj=1-ξj，dkj(ξ)=dkj+(-1)dkjξj=ξj

对于j∈Bi∩Ak，dij(ξ)=dij+(-1)dijξj=ξj，dkj(ξ)=dkj+(-1)dkjξj=1-ξj

对于j∈Bi∩Bk，dij(ξ)=dij+(-1)dijξj=ξj，dkj(ξ)=dkj+(-1)dkjξj=ξj

在乐观值准则下：

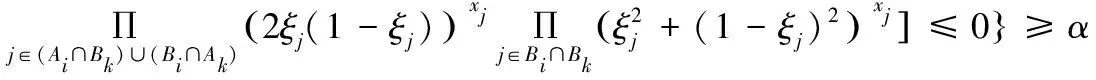
3)虚警率不确定约束条件求解

在乐观值准则下：

4)漏检率不确定约束条件求解

在乐观值准则下：

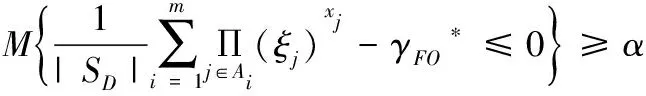
在期望值准则和乐观值准则下，利用不确定变量逆分布将测试不确定优化模型转化为，带有专家信度确定性优化选择模型：

在约束条件里，为了求解Φ-1(α)，Liu[19]给出了99-表如表1所示。其中第一行代表α的大小，即Φ(x)，第二行代表不确定度ξi的大小，即Φ-1(α)。对于ξi的函数f(ξi)，利用运算法则可知其对应的99-表如表2所示。

表1 ξ变量99-表

表2 f(ξ)变量99-表

4 实例分析

则目标函数:

表3 故障测试矩阵

虚警率约束条件：

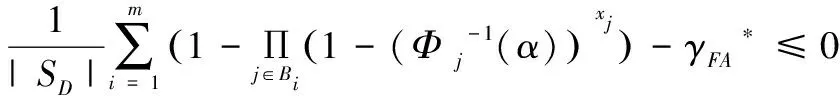
5 结论

军用飞机由于复杂自然环境和电磁环境的干扰，其PHM系统的状态监测信号发生偏移，从而引发系统虚警。为从根源上降低虚警率，必须在测试优化选择建模时考虑测试的不确定性。本文将不确定理论应用到测试性建模过程中，通过构建带有专家信度的测试不确定优化选择模型，将测试不可靠条件下的测试性建模问题转化为不确定优化问题，同时解决了基于概率论研究测试不确定性问题，无法有效获得先验概率的限制。目前，将不确定理论用于解决PHM系统中的不确定性问题研究的成果尚不多见，因此本文的研究具有很强的前瞻性，论文所研究的相关理论和模型可用于指导解决PHM系统中的其他不确定性问题，包括状态预测的不确定性、保障决策的不确定性等问题。