基于MATLAB软件的牛顿插值法理论研究

周建杰 禹仁贵

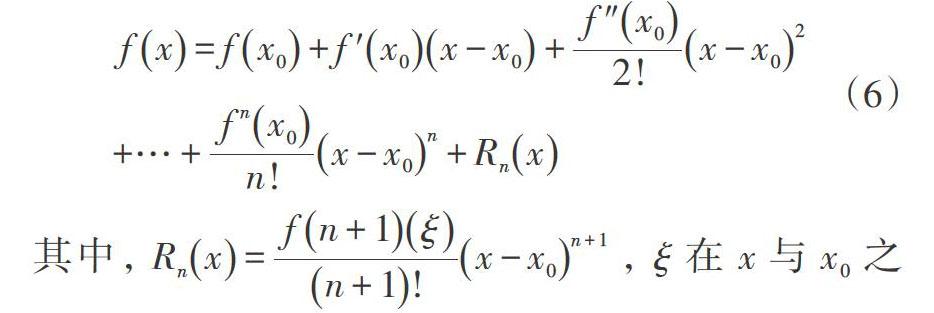
摘 要：牛顿插值法是数值计算中较为重要的方法之一。本文介绍了牛顿插值法的理论，讨论了其优缺点及与泰勒展式的关系。通过一个具体的实例，应用MATLAB软件，直观地展示了牛顿插值法的实现及其特点。

关键词：牛顿插值法;泰勒展式;龙格现象;MATLAB

中图分类号：G642文献标识码：A文章编号：1003-5168（2018）32-0010-03

Newton Interpolation Method Theory and MATLAB Realization

ZHOU Jianjie YU Rengui

（College of Information and Management Science， Henan Agricultural University，Zhengzhou Henan 450002）

Abstract： Newton interpolation method is one of the most important methods in numerical calculation. This paper introduced the theory of Newton's interpolation method， discussed its advantages and disadvantages and the relationship with Taylor's expansion.  Through a specific example， the realization and characteristics of Newton's interpolation method were shown intuitively by using MATLAB software.

Keywords： Newton interpolation method;Taylor expansion;Runge's phenomenon;MATLAB

1 研究背景

通常情況下，在科学研究和生产实践中都用函数[y=fx]来表示某种内在规律的数量关系。若[fx]在某个区间[a，b]上是存在的、连续的，但只能给出[a，b]上一系列点的函数值表（见表1）时，或者函数有解析表达式，但计算过于复杂、使用不方便只给出函数值表（如三角函数表、对数表等）时，为了研究函数的变化规律，往往需要求出不在表上点的函数值。因此，人们希望根据给定的函数表做一个既能反映函数[fx]的特性，又便于计算的简单函数[Px]，用[Px]近似表示[fx]，即[Pxi=fxii=0，1，2，…，n]。这就引出了插值问题[1]。插值问题的几何意义是：已知平面上n+1个不同的节点，要寻找一条次数不超过n的多项式曲线通过这些节点。

在我国古代，人们就开始运用插值法的思想来解决问题。隋代天文学家刘焯创立了用三次差内插法来计算日月视差运动速度;唐代杰出天文学家张遂在《大衍历》中提出了自变数不等间距的二次差内插法用于编制天文数表。此外，17世纪之后，西方数学家拉格朗日和牛顿分别讨论了非等距和等距的一般插值公式。目前，人们常用的插值方法有：拉格朗日插值、牛顿插值、埃尔米特插值、分段低次插值和三次样条插值。

理论、试验、计算是人类进行科学活动的三大方法，许多实际的科学与工程问题的解决都离不开科学计算。牛顿插值法是数值计算中较为重要的方法之一，在电力、机械、建筑科学与工程、环境科学、电信技术、计算机等学科中都有广泛应用。本文着重讨论牛顿插值法理论以及MATLAB上机实验。

2 牛顿插值法

在区间[a，b]上，函数[fx]关于一个节点[xi]的零阶差商定义如式（1）所示，[fx]关于两个节点[xi和xj]的一阶差商定义见式（2）。一般地，k阶差商就是k-1阶差商的差商，称式（3）为[fx]关于k+1个节点[x0，x1，…，xk]的k阶差商[2]。具体可以按表2的格式有规律地计算差商。

[fxi=fxi]                                 （1）

[fxi，xj=fxj-fxixj-xi]                            （2）

[fx0，x1，…，xk=fx1，x2，…，xk-fx0，x1，…，xk-1xk-x0]    （3）

借助差商的定义，牛顿插值多项式可以表示为：

[Nnx=fx0ω0x+fx0，x1ω1x+fx0，x1，x2ω2x+…+fx0，x1，…，xnωnx]     （4）

牛顿插值多项式的余项公式可以表示为：

[Rnx=fx，x0，x1，…，xnωn+1x]               （5）

其中，[ω0x=1]，[ωkx=x-x0x-x1…x-xk-1][k=1，2，…，n+1]。对于[a，b]中的任一点[x]，则有[fx=Nnx+Rnx]。

假设由表1给出的插值问题，已经得到牛顿插值多项式，如果所得插值多项式与原函数在某些点的误差较大，达不到所要求的精度，一个很自然的想法就是希望通过增加节点以提高插值多项式的次数，从而提高精度。拉格朗日插值法的基函数简单，且公式结构紧凑，如果增加节点，所有基函数都需要重新进行计算，牛顿插值法就很好地克服了这一缺陷，在多项式中只需要增加一项即可。根据差商的性质，对于在差值节点[x0，x1，…，xn]中任意位置增加或删除一个插值节点的问题，可以设计牛顿插值多项式的承袭性算法。一般认为，插值节点越多，插值多项式[Nnx]次数越高，逼近[fx]的效果就越好，但20世纪初龙格给出一个反例，随着n的增大，高次多项式插值会出现震荡现象，即龙格现象。

设[fx∈Cna，b]，一般称[fx0]为[fx]在二重节点（[x0，x0]）处的一阶差商，记作[fx0，x0=fx0]，称[fx02！]为[fx]在三重节点[x0，x0，x0]处的二阶差商，记作[fx0，x0，x0=fx02！]，依此类推，[fx]在n重节点[x0，x0，…，x0]处的n-1阶差商记作[fx0，x0，…，x0=fx0n！]。由泰勒定理[3]可知，对[x∈a，b]，有

[fx=fx0+fx0x-x0+fx02！x-x02+…+fnx0n！x-x0n+Rnx]   （6）

其中，[Rnx=fn+1ξn+1！x-x0n+1]，[ξ]在[x]与[x0]之间。由[n]重节点差商的定义和泰勒定理可知：①通过计算点[x0]处的[n]阶差商表，可以写出该点处的[n]阶泰勒展式;②通过计算点[x0]处的[n]阶导数，可以写出该点处的[n]阶牛顿插值多项式;③牛顿插值余项与泰勒余项相等，即[fx]在[n]重节点[x0，x0，…，x0]处的牛顿插值多项式与[fx]在点[x0]处的泰勒展式相同。

3 牛顿插值法的MATLAB实现

例：设有函数[fx=11+x2]，在[-5，5]上取等距节点[xi=-5+ii=0，2，4，…，10]上写出牛顿插值多项式，在[-5，5]上取等距节点[xi=-5+ii=0，2，4，…，10]上讨论牛顿插值龙格现象。

解：在MATLAB命令窗口中输入：

>>format rat

x0=-5：2：5; y0=1./（1+x0.^2）;

syms x; n=max（size（x0））;

y=y0（1）; disp（y）;

s=1; dx=y0;

for i=1：n-1

dx0=dx;

for j=1：n-i

dx（j）=（dx0（j+1）-dx0（j））/（x0（i+j）-x0（j））;

end

df=dx（1）; s=s*（x-x0（i））; y=y+s*df;

disp（y）;

end

N_n（x）=y

運行上述程序结果如下：

1/26

（2*x）/65 + 5/26

（2*x）/65 + （11*（x + 3）*（x + 5））/260 + 5/26

（2*x）/65 + （11*（x + 3）*（x + 5））/260 - （（x + 1）*（x + 3）*（x + 5））/65 + 5/26

（2*x）/65 + （11*（x + 3）*（x + 5））/260 - （（x + 1）*（x + 3）*（x + 5））/65 + （（x - 1）*（x + 1）*（x + 3）*（x + 5））/520 + 5/26

（2*x）/65 + （11*（x + 3）*（x + 5））/260 - （（x + 1）*（x + 3）*（x + 5））/65 + （（x - 1）*（x + 1）*（x + 3）*（x + 5））/520 + 5/26

N_n（x） =（2*x）/65 + （11*（x + 3）*（x + 5））/260 - （（x + 1）*（x + 3）*（x + 5））/65 + （（x - 1）*（x + 1）*（x + 3）*（x + 5））/520 + 5/26

在MATLAB命令窗口中输入：

>>x0=-5：5; y0=1./（1+x0.^2）;

x1=-5：2：5; y1=1./（1+x1.^2）;

x2=-5：0.02：5; y2=1./（1+x2.^2）;

x=-5：0.05：5;

m=length（x）;

for k=1：m

tx=x（k）; n=length（x0）;

y=y0（1）; s=1; dx=y0;

for i=1：n-1

dx0=dx;

for j=1：n-i

dx（j）=（dx0（j+1）-dx0（j））/（x0（i+j）-x0（j））;

end

df=dx（1）;

s=s*（tx-x0（i））;

y=y+s*df;

end

yx0（k）=y;

end

for k=1：m

tx=x（k）; n=length（x1）;

y=y1（1）; s=1; dx=y1;

for i=1：n-1

dx1=dx;

for j=1：n-i

dx（j）=（dx1（j+1）-dx1（j））/（x1（i+j）-x1（j））;

end

df=dx（1）;

s=s*（tx-x1（i））;

y=y+s*df;

end

yx1（k）=y;

end

figure;

plot（x，yx0，'：g'，'LineWidth'，2）;

hold on; plot（x，yx1，'--k'，'LineWidth'，1.5）;

hold on; plot（x2，y2，'-b'，'LineWidth'，1）;

grid on; xlabel（'x轴'）; ylabel（'y轴'）;

legend（'n=10插值曲线'，'n=5插值曲线'，'原曲线'）;

运行上述程序结果如图1所示。从图中可以看出，相较于[N5x]在区间[-3，3]内，[N10x]与[fx]拟合效果较好，在区间[-5，3]和[3，5]内，[N10x]与[fx]偏离较远，出现龙格现象。

4 结语

牛顿插值法可以通过计算差商表来求出，当插值节点增加或减少时，不需要像拉格朗日插值法那样重新计算。牛顿插值法具有承袭性，减少了计算量。当插值节点增多时，牛顿插值会出现龙格现象。在给定重节点处的牛顿插值多项式与该点处的泰勒展式相同。

参考文献：

[1]朱建新，李有法.数值计算方法[M].北京：高等教育出版社，2012.

[2]甄西丰.差商与牛顿插值多项式的承袭性算法[J].华中理工大学学报，2000（4）：35-38.

[3]韩云端.微积分概念解析[M].北京：高等教育出版社，2007.