一道例题的有效变式练习
——min、max函数问题研究

张 琴

(河南省衡阳师范学院南岳学院 421000)

“问题是数学的心脏，如何高效的解决问题是数学的真谛”.笔者认为在讲授“min 函数”时,可从一个简单的min问题着手分散难点,通过例题的有效变式引领学生探究, 在解题过程中既能扩散学生思维，又能帮助学生提高解题能力．

一、数学中min、max函数有效变式案例分析

1.铺垫式练习

定义符号min{p，q}含义为：当p≤q时，min{p,q}=p；当p>q时，min{p,q}=q.如：min{3,-1}=-1，min{-3，4}=-3.求min{2x,3}.

点评通过铺垫式问题的探究老师引导学生思考，辅助理解,从而达到分散难点.

2.例题练习

求min{x2-1,-2}.

点评由前面的铺垫很多学生自然想到要讨论，但有些学生会发现不需讨论.这时老师正好借此引导学生，即可将例题渗透到函数中,结合数形思想来分类讨论问题,又能帮助学生快速地理解min函数图象这个重难点.由此例题的转化铺垫,为后面的引导性问题渗透了数学思想的运用．

3.理解性变式练习

点评可将代数问题转化为函数图象问题来解决min函数，弄清min函数问题实质是在同一自变量时比较函数图象的高低来解决．在此可顺便提下最值，及函数增减性.

4.探究式变式练习

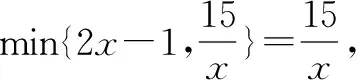
点评通过探究式变式练习的过程，老师引导学生去画函数图象，来解决实际问题.从而让学生领会到借助函数的图象，更突出了画函数图象解决min函数的问题的重要性 ，并且能全面地让学生真正地认识min函数图象的实质．

5.拓展化变式练习

(2)已知min{2x2-3x+n,-5}=-5，求实数n的取值范围；

(3)已知当-1≤x≤2时，min{x2-2x-3，mx-m}=x2-2x-3, 求实数m的取值范围．

点评通过近年来中考试题等新颖试题的要求 ，其实本质上要求学生以数形结合思想来解决函数问题,理解函数图象是解决函数问题的根基．

6.类比变式练习

设xi(i=1,2,3,…,n)为任意代数式，我们规定：y=max{x1,x2,…,xn}表示x1,x2,…,xn中的最大值，如y=max{1，2}=2。

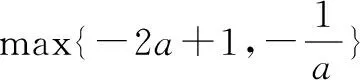
点评①类比变式练习可以高效地培养学生思维综合，即实现数学学习中系统方法的掌握,又可以将相应知识之间有效地结合在一起，起到巩固作用.

②类比思维可以高效地培养学生的数学解题、数学公式推导、扩展解题思维,同时也形成了对学生的数学思维以及逻辑思维等各方面能力的培养和创新思维的培养.

二、数学变式教学的实践成效与反思

笔者认为在我们实践数学变式教学中，教师可以精心设计数学中例题的有效变式的题目，题目可以步步深入地引导学生，并且让学生从一系列题目“变化”的现象中发现问题始终“不变”的本质特征，又能让学生从事物“不变”的现象中进一步探究事物“变”的现象和规律. 并将学生带出题海战术和应试教育，起到事半功倍.

1.变式教学是有效的，可提高学生的学习兴趣，有利于数学知识的掌握，有利于学生能力的培养和思维水平的提升.

2.在变式教学中应在难度、数量和学生的参与度上有所把握，才可以使变式教学事半功倍.实践证明，多进行变式教学，能帮助学生更加深刻地认识到该数学问题的本质特征.有利于培养学生的数学反思能力.

3.有效的数学变式能有效地帮助学生在面对同类型题时一看即有思路，不但为学生省下在遇到新题的重复精力及恐惧感，而且在老题型的思维发散上反倒锻炼了学生数学思维.

笔者通过自己大量练习中考最值问题试题以及在教学方面的实践中，总结出近年来中考试题等新颖试题的要求,其实本质上要求学生以数形结合思想来解决函数问题,理解函数图象是解决函数问题的根基.因此笔者将min、max函数问题通过铺垫式练习，引导学生将问题渗透到数学思想中，帮助学生辅助理解,分散难点.