静电场求解方法的探讨

（昌吉学院物理系 新疆 昌吉 831100）

1 静电场的概念及规律

1.1 静电场的概念

静电场，通常是由静止电荷所激发的一种场。它存在于电荷周围，是一种看不见摸不着的特殊形态的物质，其基本特征是对放入其中的电荷有作用力。［1］两个静止点电荷之间的相互作用就是通过静电场来传递的，其中，它们之间的相互作用力F⇀的大小与它们各自所带的电荷量q1和q2的乘积成正比，与它们之间的距离r的平方成反比；同时，作用力的方向沿着两点电荷之间的连线，同号电荷相互排斥，异号电荷相互吸引，其数学表达式如下：

1.2 电场强度

（2）点电荷系的场强：

（3）电荷连续分布的带电体的场强：

其中，不同形状带电体的电荷元dq可以有不同的表示形式，如：线电荷密度表示为λdl，面电荷密度表示为σds，体电荷密度表示为=ρdV。

1.3 电场强度通量

在电场中穿过任一曲面S的电场线条数称为穿过该面的电场强度通量，其数学表达式为

1.4 静电场的基本定理

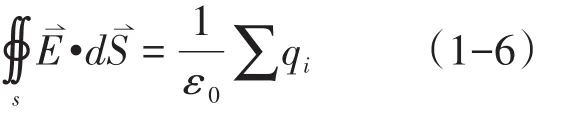
（2）静电场的环路定理：在静电场中，电场强度沿任一闭合路径的线积分恒为零，静电场的环路定理表明静电场是保守场，其数学表达式为

2 静电场的求解方法

2.1 叠加法求静电场

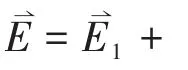
例题：已知一个边长为a的正方形，其四个顶点上放置点电荷，电荷量分别为q（q＞0），2q，-3q和2q（如图1所示），求该正方形中心O点的电场强度。

解析：因正方形四个顶点上分别有四个点电荷，利用点电荷在空间激发电场的公式（1-2），可求出各个点电荷在O点产生的电场强度的大小分别是：

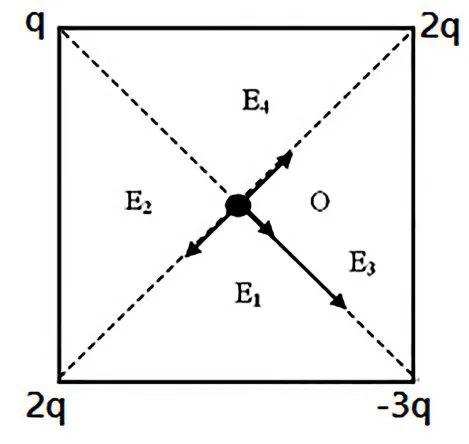
图1 点电荷的分布图

2.2 高斯定理求静电场

高斯定理是静电学中的一个非常重要的定理，主要用于求解电荷分布具有对称性的场强，由公式（1-6）可知，具有高度对称性的带电体，可在周围空间激发具有高对称性分布的电场。［3-4］以下介绍三种典型的带电体：

（1）带电体具有球对称性：如点电荷、电荷均匀分布的球面或球体，等；

（2）带电体具有轴对称性：如电荷均匀分布的无限长直线、无限长圆柱体或圆柱面，或者是无限长均匀带电的同轴圆柱面；

（3）带电体具有面对称性：如电荷均匀分布的无限大平面或平板。

依据高斯定理的文字表述和计算公式（1-6），计算电场场强时，首先根据带电体上电荷分布的对称性，分析出由其激发的场强分布的对称性，依据场强的分布选取合适的闭合曲面作为高斯面，其中，选取的高斯面上各点的电场强度大小相等，方向与其面元的法线方向相同，这样便于场强E⇀与面元dS⇀的点积运算。最后，利用高斯定理中的面积分求出场强的分布。下面是具体例题应用高斯定理求场强：

例题：如图2所示，一半径为R的带电球体，其电荷体密度分布为ρ=Ar (r≤ R)，ρ=0 (r＞ R)，A为大于零的常量。试求球体内外的场强分布及其方向。

图2 半径为R的带电球体

解析：（1）当r＜ R时，在球内取半径为r、厚为dr的薄球壳，该壳内所包含的电荷为 dq=ρdV=Ar⋅4πr2dr=4πAr3dr

得到E1=Ar2/(4ε0)，方向沿径向向外；

（2）当r＞R时，在球体外作一半径为r的同心高斯球面，按高斯定理有

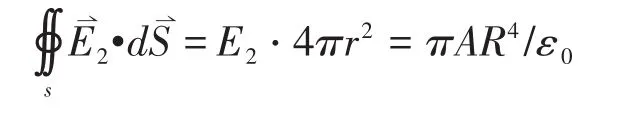
得到 E2=AR4/(4ε0r2)，方向沿径向向外。

2.3 分离变量法求静电场

分离变量法是求解偏微分方程定解问题的基本方法。在解线性偏微分方程的混合问题或边值问题时，先求满足边界条件的变量分离的特解，再利用叠加原理，做这些特解的线性组合，得到定解问题的解，这就是分离变量法。

通常情况下，静电场的电势所满足的微分方程为：

是一个泊松方程，当所处空间为自由空间，及无自由电荷时，静电场的电势所满足的微分方程为：

该方程为拉普拉斯方程，借助一定的边界条件，该方程可利用最有效的方法——分离变量法进行求解。在此，利用分离变量法求解静电势举例如下：

例题：将半径为R0的接地导体球置于一匀强电场E⇀中，如图3所示，求空间电势？

图3 半径为R0的导体球置于一个匀强电场

解析：由题意可知，该问题应选择球坐标系，而且空间中电场分布具有轴对称型，于是具体的求解过程如下：

∵在自由空间，静电场满足的方程为：

利用分离变量法，可知，上方程的通解为：

利用边值关系可知：

最后，确定常数：

∴该问题的解为：

由以上例题可知，分离变量法适用于具有对称性较好的实际问题，具体的解题过程可分为以下三步：第一步根据题意确定坐标系（如球坐标系、柱坐标系）；第二步依据所选的坐标系，待求的偏微分方程的解通常可表示为三个独立变量函数的乘积，及其中的每一个函数仅是一个坐标变量的函数，这样，通过分离变量法就将偏微分方程转化为三个常微分方程。第三步分别求解出三个常微分方程的通解，同时，依据边界条件确定具体的系数，从而最终得到方程的有效解。这类问题随具体情况的不同需要选择不同的坐标系，因此，解题关键在于选取合适的坐标系。

2.4 格林函数法求静电场

格林函数法是一种通过借助格林公式，将静电场边值问题转化为求解相应的格林函数的问题，具体方法就是将非齐次边界条件下泊松方程的求解问题，简化为齐次边界条件下的拉普拉斯方程的求解问题（第二类格林函数除外）。

上面提到的点电荷是电荷分布的一种极限情况，它可以看作一个体积很小而电荷密度很大的带电小球的极限。若电荷分布于小体积ΔV内，当体积ΔV→0时，体积内的电荷密度ρ→∞，而保持总电荷不变，所谓点电荷就是这种电荷分布。处于原点上的单位点电荷的密度用函数ρ(x)表示。

设有包含x′点的某空间区域V，在V的边界S上有边界条件：

则方程（1-12）同时满足边界条件（1-13）的解，称为泊松方程在区域V的第一类边值问题中的格林函数。若在S上有另一边界条件：

则方程（1-12）同时满足边界条件（1-14）的解，称为泊松方程在区域V的第二类边值问题中的格林函数。

这方程中的∇2算符是对x点的微分算符。如果是无界空间，在x′点上一个单位点电荷在空间中某点x处激发的电势为：

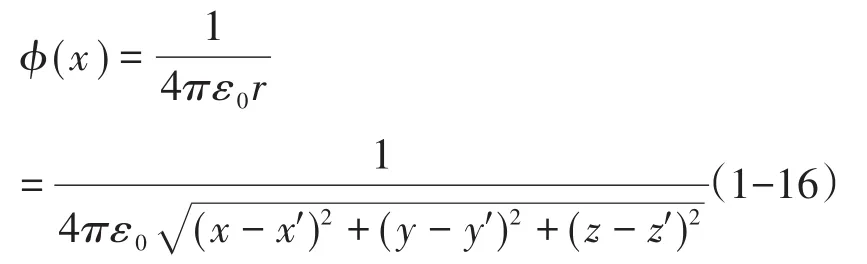
式中r为源点x′到场点x的距离。因此，无界空间的格林函数为

2.5 镜像法求静电场

镜像法是求解边值问题的一种特殊解法。［5］其理论依据是唯一性定理和叠加原理，其基本思想是用假想的集中电荷（镜像电荷）来等效代替分界面上的分布电荷对场的贡献，而无需求出方程的通解，只需求解镜像电荷和区域内给定电荷共同产生的电位，下面举例说明这方法的应用。

例如，真空中放置一个半径为R0的接地导体球，距球导体球心O为a(a＞R0)的位置有一个点电荷Q，求该电荷体系在空间各点产生的电势（如图4）。

图4 （a）半径为R0的接地导体球；（b）等效示意图

由此可见，假象电荷Q′的位置和大小是可以唯一确定的，把假象电荷Q′又称作镜像电荷。

由原电荷Q和镜像电荷Q′激发的总电场，在满足导体面上ϕ=0的边界条件下，可以得到空间中电场的唯一解。于是，球外任一点P（如等效示意图4b）的电势为：

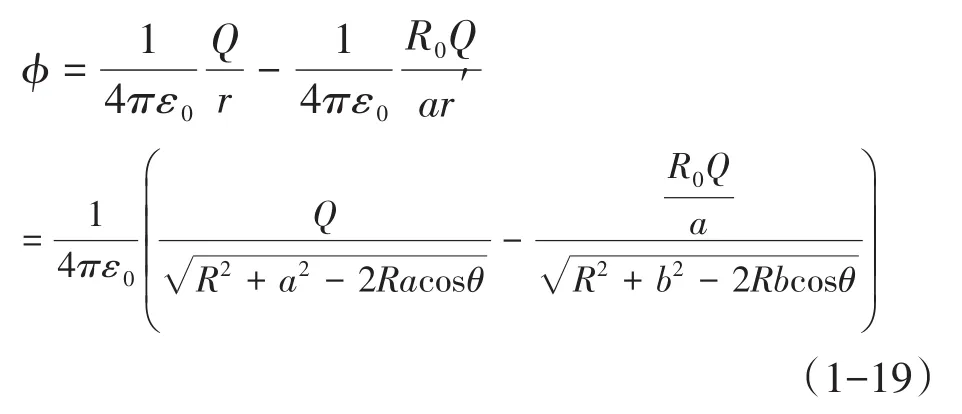
式中r为电荷Q到P点的距离，R为球心O到P点的距离，θ为OP与OQ的夹角。

3 结论

本文通过对各种静电场求解方法的探究，一方面，为静电场的求解提供了完整的方法，另一方面，通过具体的实例对每种求解方法进行应用，使得读着可以更好地理解和应用每一种方法，为静电场的求解提供合理可行的方法。