任意边界下多跨梁弯曲计算及其工程应用

熊剑锋，闫肖杰，江璞玉，刘均，程远胜*

1华中科技大学船舶与海洋工程学院，湖北武汉430074

2中国舰船研究设计中心船舶振动噪声重点实验室，湖北武汉430064

0 引 言

多跨梁模型是船舶、桥梁领域常见的力学模型。目前，国内外针对任意边界条件下梁结构的振动与冲击方面的研究较多。例如，文献［1-3］提出了一种改进的傅里叶级数方法（Improved Fourier Series Method，IFSM），该方法在传统的余弦傅里叶级数的基础上，增加了4项正弦级数，是一种半解析法（Semi-Analytical Method，SAM）。经数学证明，此方法可扩展并收敛于任意一个函数，通过对弹性边界条件下的梁、板的振动分析，验证了此方法的正确性。Xu和Li［4］则在传统的傅里叶余弦级数的基础上添加了4项多项式级数（此方法也可消除傅里叶级数在边界上的不连续问题），并研究了动载荷下多跨梁响应的问题。此外，周渤和石先杰［5］也利用该级数形式研究了任意边界条件下多跨梁振动的问题。目前，针对任意边界条件下梁或多跨梁弯曲的问题，主要采用经典的结构力学法或有限元法（FEM）求解，前者需要先求解三弯矩方程或五弯矩方程，然后再由求得的节点弯矩值得到每跨位移，进而利用其他物理量与位移的微分关系得到待求解的物理量结果，而后者则首先需要在前处理中建立模型，然后再求解，因此整个过程耗时较长，且当几何参数变化时修改也较麻烦。

在滚装船和大型舰船中，车辆装载甲板及机库甲板上的强横梁及纵桁等主要承力构件均可被视为一种多跨梁结构，在轮印载荷下，其承受的载荷大小与作用位置具有不确定性。因此，在多种轮印载荷工况下找到多跨梁的最危险工况，对于船舶结构的安全校核及装载方案的设计具有重要意义。为此，Jeon和Kim［6］研究了遗传算法应用于最危险工况分析的算法性能，成功找到了多个经典数学问题的最危险工况。方陆鹏等［7］将轮印载荷简化为集中力，制作了轮印载荷下连续多跨梁结构模型的试验装置，并对比了弯矩的理论值与实验值，结果表明两者基本一致。康杰豪等［8］采用有限元法与遗传算法相结合的方法，首先利用有限元法计算多跨梁结构各载荷工况下的响应值，然后结合遗传算法找到在轮印载荷作用下各跨弯矩或剪力的最大、最危险工况，以此对多跨梁结构进行优化设计。但是有限元法计算较为耗时，而传统的遗传算法所需的计算设计点较多，导致总体计算效率不高，且由于轮印载荷作用位置采取的是离散取值，故无法找到更精确的载荷危险作用工况。

鉴于此，本文将利用IFSM方法并基于哈密顿原理，首先推导出任意边界条件下多跨梁弯曲问题的平衡方程，并结合边界条件联立求解，然后通过与有限元计算结果的对比，验证所提方法的正确性，最后将该方法与处理连续变量优化问题的遗传算法进一步结合，求解轮印载荷位置处于连续变化情况下多跨梁的最危险工况，以获得其更精确的布置工况。

1 连续多跨梁弯曲问题理论计算

1.1 物理模型

如图1所示，假设n跨连续梁第i跨的物理参数为li，Ei，Ii，分别指第i跨的跨长、弹性模量和剖面惯性矩。对于边界上弹簧的刚度系数，规定如下：k0，K0分别指连续梁的首端位移弹簧及转角弹簧的刚度系数；kn，Kn分别指连续梁的尾端位移弹簧及转角弹簧的刚度系数；ki指中间支撑位移弹簧的刚度系数，在其上作用一个任意形式的横向弯曲载荷q（x）。通过改变各弹簧的刚度系数，即可模拟任意一种边界条件。例如，当模拟两端为刚性固定、中间简支时，仅需将两端的弹簧刚度系数 (k0，K0，kn，Kn)及中间简支的弹簧刚度系数ki均设置为无穷大即可，对于模拟自由边界，仅需将各弹簧的刚度系数设置为0即可。

图1 任意边界条件的多跨连续梁模型示意图Fig.1 Schematic diagram of the multi-span continuous beams model under arbitrary boundary conditions

1.2 模型半解析求解

1.2.1 位移级数的表达形式

对于任意边界下的连续梁第i跨位移函数，可以由如下 IFSM［2］形式表示：

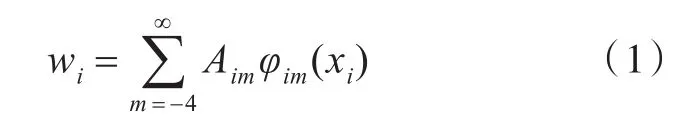
其中，

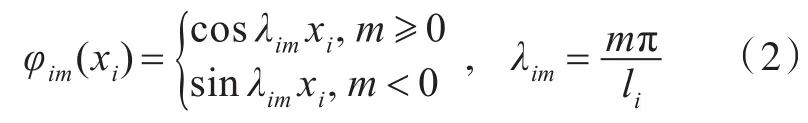
式中：wi为连续梁第i跨的位移；φim为形函数，其中下标m为每项级数的整数序号；Aim为形函数的系数；xi为连续梁第i跨范围内某个点的位置坐标；li为连续梁第i跨的长度。

上述位移级数形式在传统的傅里叶余弦级数形式的基础上，增加了4项傅里叶正弦级数，此形式克服了单一形式的傅里叶级数在边界上的不连续或跳跃现象。从数学上可知，该级数形式可扩展并收敛于任意一个函数f（x）。在实际计算时，位移级数上限值取为某一正整数M，即级数的截断数，每个位移wi共包含M+5个未知系数Aim，而求解这n×（M+5）个未知系数则是关键。

1.2.2 边界条件处理

针对图1所示的n跨连续梁结构，其首端边界方程可分别由式（3）和式（4）表示，尾端边界方程可分别由式（5）和式（6）表示：

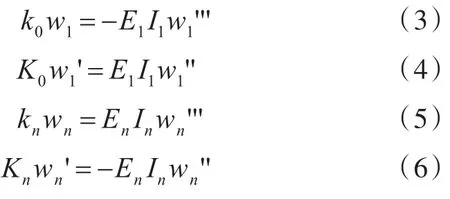
式中，wn，En，In分别为尾端边界处梁的位移、弹性模量和剖面惯性矩。

对于中间第 i个弹簧（0＜i＜n），其对应的边界连续条件可描述为

对于n跨连续梁结构，共可得到4+4（n-1）=4n个边界方程。将位移函数式（1）代入到这4n个边界条件中，并将位移函数的某4n个系数视为待求量进行求解，可得到这4n个系数与剩下的n×（M+1）个系数之间的关系式。假设每跨位移级数的-2，-1，1，2项为待求量，而剩余的为独立变量，则该关系式可表示为

式中，Cb为Aix和Aiy形函数系数之间的关系矩阵，其中，

此时，独立的未知系数的个数剩下n×（M+1）个，由此构造出的位移函数即可满足该边界条件，并表示为

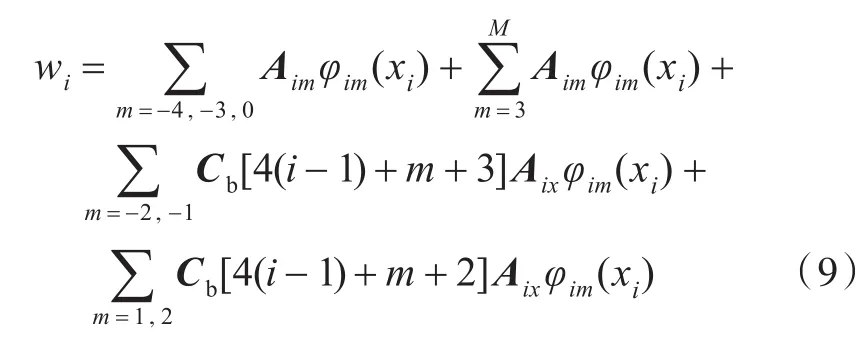
1.2.3 基于哈密顿原理推导平衡方程

根据哈密顿原理，可推导出任意边界条件下连续梁在横向载荷作用下的弯曲平衡方程，即

其中，

式中：UP，US分别为连续梁的应变能和边界上的弹性势能；W为外力功；δ为一次变分。

将式（11）～式（13）代入式（10）中，并将满足边界条件的位移表达式（9）代入式（10）中，运用伽辽金方法得到关于n×（M+1）个独立系数的代数方程组，然后求解该方程组，即可得到n×（M+1）个未知系数值。将这些系数值回代到式（9）中，得到该边界条件下的位移，根据梁结构的应力、转角、截面弯矩、截面剪力整体与位移的微分关系，即可求得相应的物理量。

1.3 算例验证

为验证本文解析法的正确性，基于某三跨梁模型设计了2种边界条件进行计算。边界条件1模拟的是两端固支、中间支座垂向固定的情况，如图2所示。边界条件2模拟的是弹性支撑下多跨梁的情况。为计算简便，梁截面形状和材料属性沿长度方向均相同，各跨距li均为10 m（总长L=30 m），弹性模量E=210 GPa，泊松比 ν=0.3。梁截面为T型材，腹板高400 mm，腹板厚8 mm，面板宽150 mm，面板厚14 mm，带板宽1 000 mm，带板厚15 mm。假设该三跨梁受到了3组轮印载荷作用，每组轮印载荷简化为2个集中力，分别为：F1，1=80 kN，F1，2=120 kN；F2，1=60 kN，F2，2=60 kN；F3，1=120 kN，F3，2=80 kN。每组轮印载荷集中力之间的间距 D1，D2，D3分别为 4，6，4 m。每组轮印载荷的首个集中力与连续梁最左端支座的间距X1，X2，X3分别为5.8，11.8，20.5 m。

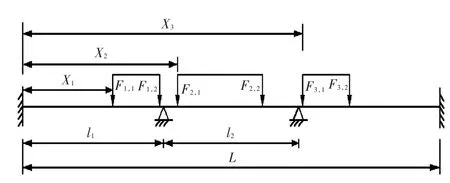
图2 边界条件1下的三跨梁模型示意图Fig.2 Schematic diagram of the three-span beams model under boundary condition 1

计算边界条件1时，将两端的位移弹簧刚度系数取为较大值来模拟，均设为k0=kn=1×1010N/m，两端的转角弹簧刚度系数均设为K0=Kn=1×1010（N·m）/rad。边界条件2模拟的是弹性支撑下的多跨梁情况，计算时将两端的位移弹簧刚度系数均设为k0=kn=1×108N/m，转角弹簧刚度系数均设为 K0=Kn=1×103（N·m）/rad，中间支座刚度系数分别设为 k1=5×107N/m，k2=7×107N/m。表1所示为边界条件1下截断数M取值对位移结果的影响。表2所示为本文方法和有限元法计算得到的各跨最大位移值的对比。图3和图4所示为2种边界条件下多跨梁的整体位移、截面弯矩及截面剪力计算结果与有限元结果的对比。

由表1可以看出，当截断数M=10时，整个计算趋于稳定，计算结果的收敛性较好。由表2可以看出，两种方法计算结果的误差较小。

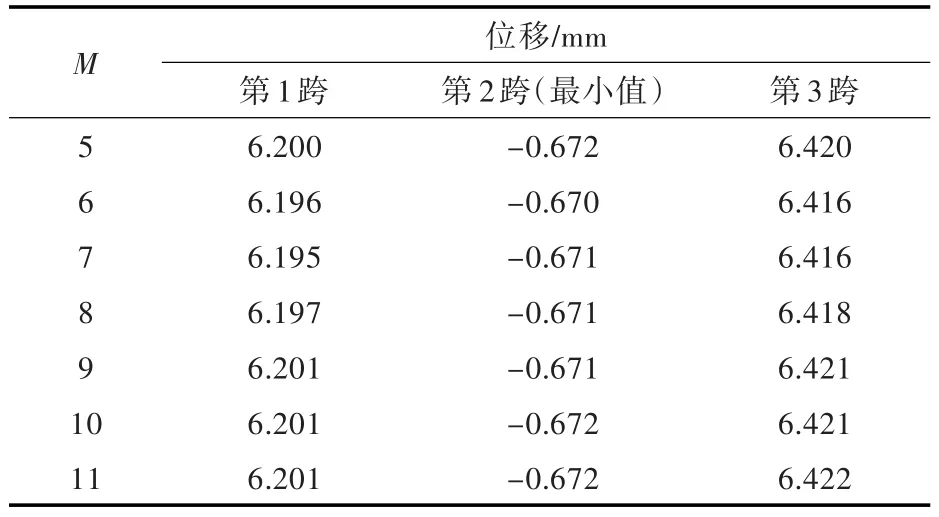
表1 边界条件1下M取值对位移结果的影响Table 1 The impacts of M value on displacement under boundary condition 1

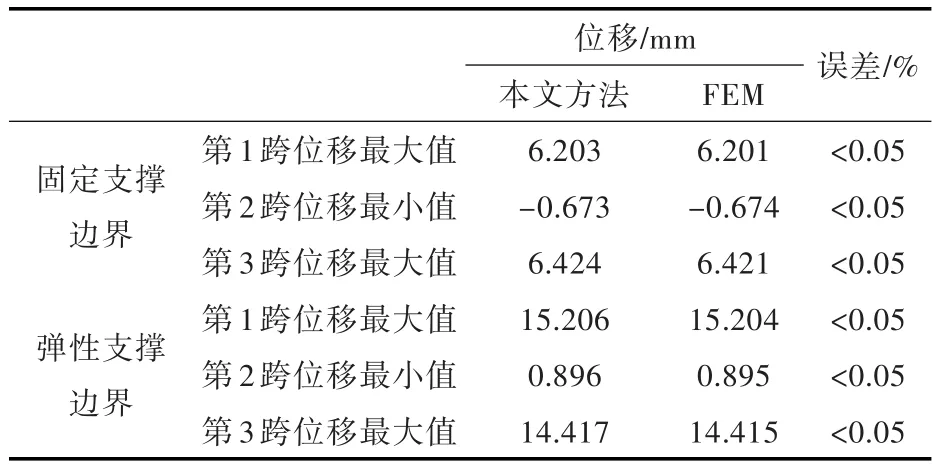
表2 各跨位移计算结果对比Table 2 The comparisons of calculated displacement for each span

图3 边界条件1下本文方法与有限元计算结果对比Fig.3 Result comparisons of the proposed method and FEM under boundary condition 1

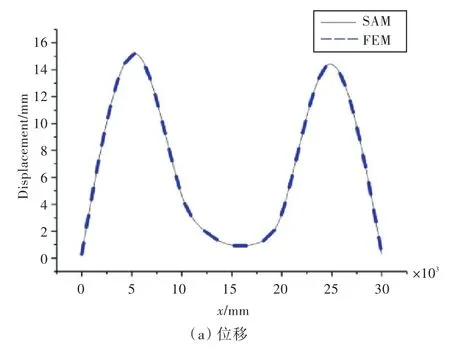
图4 边界条件2下本文方法与有限元计算结果对比Fig.4 Result comparisons of the proposed method and FEM under boundary condition 2

由图3和图4可以看出，剪力图为一系列水平直线，而本文所选用的正弦、余弦形式的形函数对于水平直线模拟需较多的项数，综合考虑，将截断数取为M=40。综合表2及图3和图4的计算结果，可看出本文方法计算得到的整体位移、截面弯矩及截面剪力与有限元计算的结果基本重合，验证了本文方法的正确性。同时，本文方法相对于有限元法计算便捷，设置简单，故有较好的工程应用价值。

2 轮印载荷下多跨梁最危险工况分析

2.1 物理模型

轮印载荷作用下多跨梁最危险工况的问题分析可描述如下［8］：给定多跨梁几何结构、轮印载荷组的数量及轮印载荷大小，寻求轮印载荷作用下的最危险布置工况，即使某一个跨梁的截面弯矩、截面剪力或整体位移取得最大值。由于轮印载荷布置位置的搭配较多，很难直接判断出多跨梁产生最大内力时所对应的最危险工况位置，故借助遗传算法对该问题进行优化计算。

图5所示为轮印载荷作用下多跨梁物理模型。假设有e组轮印载荷作用于多跨梁上，第j组轮印载荷中轮印载荷个数为 sj，Fj，a为第j组轮印载荷中第a个轮印载荷的大小，Xj为第j组轮印载荷的首载荷与多跨梁左端的间距，Dj，a为第j组载荷第a个轮印与第a+1个轮印之间的间距。

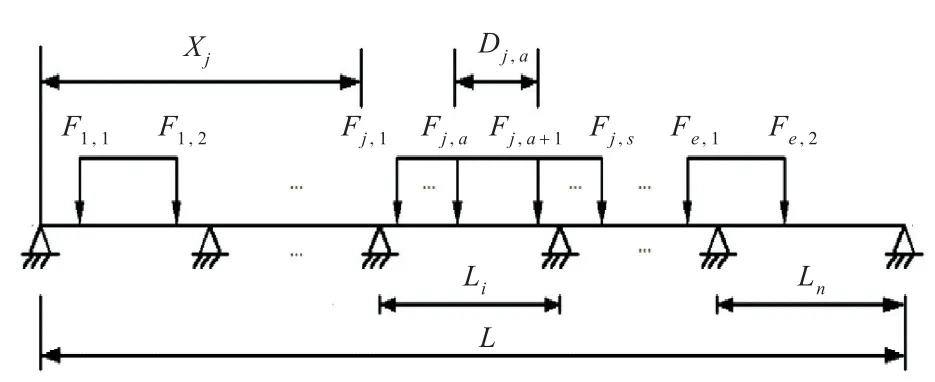
图5 多跨梁几何模型及其轮印载荷示意图［8］Fig.5 Schematic diagram of the multi-span beams model under multiple patch loading［8］

2.2 数学模型

2.2.1 设计变量

在分析轮印载荷作用下多跨梁最危险工况时，变量为各轮印载荷的布置位置。对应上述物理模型，当一组轮印中的首载荷（一组轮印载荷中的第1个载荷）位置确定时，该组轮印载荷的布置位置也就相应得到确定，故以每组轮印的首载荷与多跨梁左端的间距Xj作为该问题的设计变量。

2.2.2 目标函数

在分析轮印载荷作用下多跨梁最危险工况的目标函数为多跨梁上某跨的最大弯矩Mi或最大剪力FSi或最大变形wmax时，每个载荷布置工况下的目标函数值通过本文推导的半解析法进行求解，结果表明具有较好的精度，且相对于有限元法极大地减少了计算时间。

2.2.3 约束条件

在实际船舶的装载甲板上，相邻车辆之间的间距需要满足一定的要求，因此在轮印载荷作用下多跨梁最危险工况分析的约束条件为相邻2组轮印载荷的间距大小。约束条件如式（14）所示，式中Con1j，Con2j分别为第j组与第j+1组轮印载荷之间需要满足的最小间距及最大间距。

2.3 计算实例

运用本文多跨梁弯曲计算方法并结合遗传算法对上述优化问题进行求解。为方便对比，本文选取文献［8］中的方案2进行计算。该方案的几何参数与截面参数及每组载荷的数量、大小和间距均与2.1节算例验证所用的三跨梁相同，而每组载荷的首载荷与多跨梁左端的间距X1，X2，X3是需要求解的设计变量，其取值范围分别为0.5～6 m，10～14 m和20～25.5 m。约束条件为相邻2组轮印载荷之间的最小间距不小于1 m，最大间距不大于5 m。边界选用两端刚性固定、中间支座垂向固定的约束条件，即首、尾两端的位移弹簧刚度系数均设为1×1010N/m，两端的转角弹簧刚度系数均设为1×1010（N·m）/rad，而中间的位移弹簧刚度系数设为1×1010N/m。使用Matlab软件自带的遗传算法ga函数寻求最危险工况的结果，该函数可以处理设计变量连续取值的优化问题。计算时，种群个数设为100个，遗传代数设为100代。最终优化结果与文献［8］计算结果的对比如表3所示。

由表3可以看出，相比文献［8］，由于本文采用的遗传算法可以处理设计变量连续取值的优化问题，所以能够找到更精确的最危险轮印载荷布置工况。该工况的最大弯矩或最大剪力比文献［8］的工况更大，同时，设计变量连续取值也更贴近工程实际，这是因为车辆在装载甲板上的移动是连续的，而不是阶跃的。

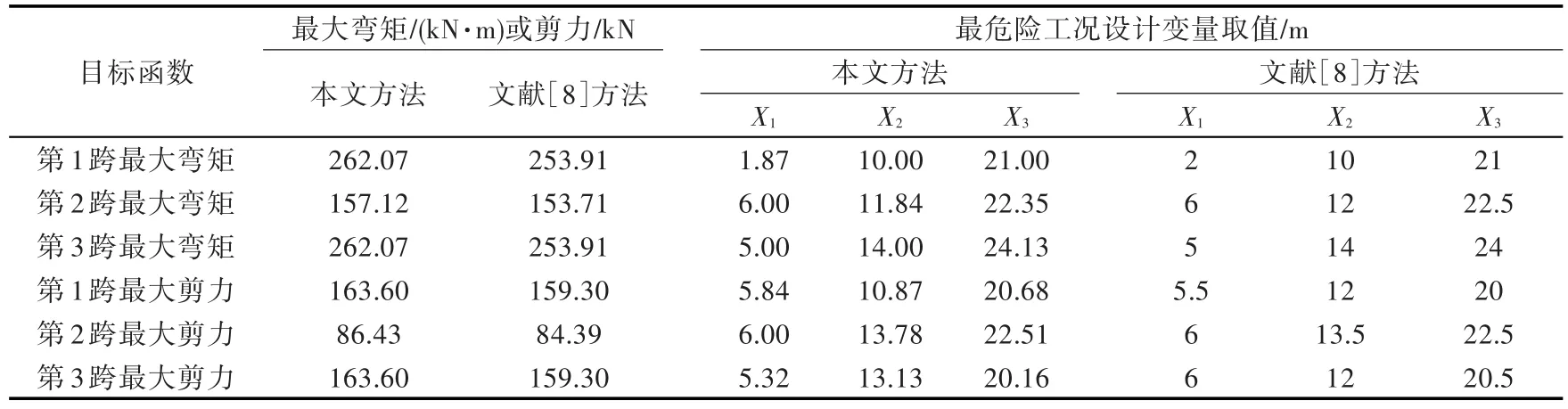
表3 多跨梁最危险工况计算结果Table 3 Numerical results of the worst-case analysis of multi-span beams

3 结 论

本文基于能量原理并结合边界条件，分析了任意边界条件下连续多跨梁结构的弯曲问题。通过将本文方法计算的结果与有限元法计算结果进行对比，验证了本文方法的正确性。运用此方法分析轮印载荷下多跨梁的最危险工况，得到了满意的结果，其计算精度较高，耗时少。根据本文的研究，主要得到如下结论：

1）推导的计算方法随着傅里叶级数截断数的增加，计算结果很快收敛，数值稳定性较好；与算例的有限元法计算结果相比，计算的位移误差小于0.05%。同时，由于基于能量原理，本文计算过程不需要平衡方程，故易于推广到板结构及其他更复杂的结构。

2）在计算分析轮印载荷下多跨梁最危险工况时，运用此方法得到了更精确的最危险布置工况。