巧添“隐形圆”解决初中“几何最值与路径”问题

摘 要：几何最值与路径问题能较好地考查同学们的几何探究与推理能力及数学思想方法的运用。有些立意新颖、构思巧妙的中考题目，将圆隐藏在已知条件里，隐晦地考查圆的有关知识。解题时，需要通过分析探索，发现这些隐圆，做到图中无圆，心中有圆。

关键词：几何最值;隐形圆;定边对定角;定点定长;夹角定位;圆的定义;动点轨迹

初中几何中的最值问题是指在一定的条件下，求平面几何图形中某个确定的量（如线段长度、角度大小、图形面积）等的最大值或最小值。在近几年各地中考中，几何最值与路径问题屡屡受到命题者关注，一批立意新颖、构造巧妙的新题、活题脱颖而出。此类问题不仅涉及平面几何的基础知识，还涉及几何图形的性质、平面直角坐标系、方程与不等式、函数知识等，能很好地考查同学们的几何探究、推理能力及数学思想方法的运用。本文结合笔者的教学实践与这几年的中考题谈谈初中几何“与动点有关的几何最值与路径”问题的求解策略。

一、 几何最值的理论依据与基本模型

求解几何最值的基本依据是：①两点之间线段最短。②垂线段最短。③在三角形中，两边之和大于第三边，两边之差小于第三边。求几何最值问题的基本方法有：特殊位置与极端位置法;几何定理（公理）法;数形结合法等。与圆有关的常用模型如下：

模型1：如图1，当点P是⊙O外一点，直线PO分别交⊙O于点A、B两点，则线段PA的长是点P到⊙O的最短距离，线段PB的长是点P到⊙O上的点的最长距离。

理由：在过点P另做直线交⊙O于点A′、B′，则有PA=PO-OA=PO-OA′PB′（三角形两边之和大于第三边）。

模型2：如图2，当点P是⊙O内一点，直线PO分别交⊙O于点A、B，则线段PA的长是点P到⊙O上的点的最短距离，线段PB的是点P到⊙O上的点的最长距离。

理由：在⊙O另取不同于点A、B的点A′、B′，则有PA=OA-OP=OA′-POPB′（三角形两边之和大于第三边）。

模型3：定边对定角

已知点A、点B是定点，平面内的动点P满足∠APB=n°（n为定角），根据“经过不在同一条直线的三个点有且只有一个圆”可知动点P的运动路径是圆弧。当0°<n<90°时，可知点P的运动轨迹是以AB为弦的一段优弧APB（A、B两点除外），如图3;而当180°>n>90°时，可知点P的运动轨迹是以AB为弦的一段劣弧AB（A、B两点除外），如图4;而当n=90°时，点P在以AB为直径的圆弧上，“定边对直角”是“定边对定角”的特例，如图5。

注：这是动点P的运动轨迹仅做出了弦AB一侧的情形，由对称性可知，AB的另一侧还存在一条弧满足条件。

以上的三种模型，属于单动点问题。在运动过程中动点的运动路径圆（或圆弧）并不直接给出，此时需要根据条件把“隐圆”勾画出来，具体来说“隐圆”一般有如下呈现方式：①定点定长;②定弦定角;③圆的定义。如何确定“隐形圆”的圆心与半径呢？下面结合各地近几年的中考热点考题进一步说明如何利用“隐形圆”巧妙解题。

二、 走进中考，提升思维

（一） 定边对定角：确定动点的位置在确定的圆弧上，再求线段长度的最值

【例1】 （泉州七中2019届中考模拟试题）如图6，∠MON=45°，矩形ABCD的顶点A、B分别在OM、ON上运动，若AB=2，BC=1，则OC的最大值是。

分析：如图7，假设矩形ABCD不动，让点O运动。作以AB为斜边的等腰直角三角形△APB，由AB=2，∠APB=90°，知PA=PB=2，此时圆角角∠AOB=45°，所以动点O在⊙P上运动，OP=AP=2。当O、P、C三点共线时，OC有最大值=OP+PC=2+5（由∠PBC=135°，PB=2，BC=1，可求出PC=5）。

点评：本题的解题很有技巧，把动矩形化为动圆，而定点O在圆上，再用圆与三角函数的知识求线段长。

利用“定边对定角”模型解题的关键是：首先要有“动中找静”求动点的轨迹的意识，在目标动点处看看是否存在定角。若存在，再寻找该定角是否有相对的定边，一旦两者都具有，就自然会产生“圆弧型”路径，然后找其圆心，定其半径，求其弧长或最值即可。

（二） 圆的定义法：到定点的距离为定长的所有动点在确定的圆上，再解决路径长度

在初中阶段，动点的路径常见有三类：直线型路径、圆弧形路径、来回型路径。求动点的路径长的问题，关键是先分析路径的形状。

1. 直线型路径

【例2】 （2017江苏扬州）已知正方形ABCD的边长是4，点P是AB边上的一个动点，连结CP，过点P作PC的垂线交AD于点E，以PE为边作正方形PEFG，顶点G在线段PC上，对角线EG、PF相交于点O。当点P从点A到点B的运动时，求点O经过的路径长。

分析：（1）法一：如图8，Rt△APE的外接圆是以斜为PE为直径的⊙M，连结OM、AM。正方形EFGH中，∠EOP=90°，則有OM=12PE=AM，所以点O一定在△APE的外接圆上。易知∠1=∠2=45°，所以动点O以必在直线AC上运动，再找临界点可知：点O的起点位置是点A，点O的终止位置是点线段AC的中点，所以点O经过的路径长=12AC=22。

法二（双垂直法）：如图9，过O作OH⊥AB于点H，过O作OK⊥AD于点K，易证明△OHP≌△OKE（AAS），所以OH=OK，根据“到角的两边距离相等的点在角的角平分线上”，所以OA平分∠BAD，即点O在AC上运动。剩下同法一可求出。

点评：本题中“用夹角定位法”，可知动点O的路径是直线型。“用夹角定位法”确定动点路径的一般步骤是：①找定点，一般是目标动点的起点与终点;②连结目标动点和该定点，证明它与某直线的夹角确定;③采用临界点法，找出动点的起点与终点，求出路径。

2. 圆弧形路径

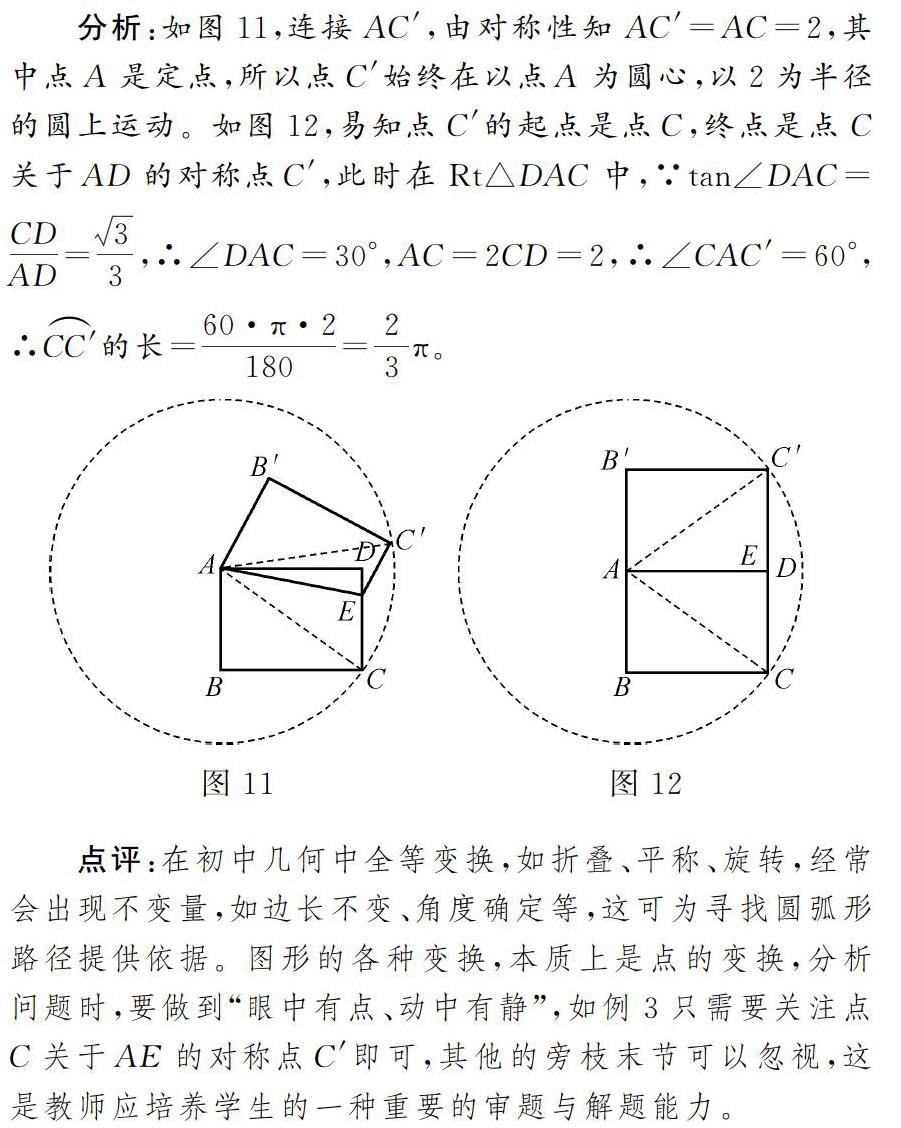
【例3】 （2017年江苏宿迁）如图10，在矩形纸片ABCD中，已知AB=1，BC=3，点E在边CD上移动，连接AE，将多边形ABCE沿直线AE翻折，得到多边形AB′C′E，点B、C的对应点分别为点B′、C′。在点E从点C移动到点D的过程中，求点C′运动的路径长。

分析：如图11，连接AC′，由对称性知AC′=AC=2，其中點A是定点，所以点C′始终在以点A为圆心，以2为半径的圆上运动。如图12，易知点C′的起点是点C，终点是点C关于AD的对称点C′，此时在Rt△DAC中，∵tan∠DAC=CDAD=33，∴∠DAC=30°，AC=2CD=2，∴∠CAC′=60°，∴CC′的长=60·π·2180=23π。

点评：在初中几何中全等变换，如折叠、平称、旋转，经常会出现不变量，如边长不变、角度确定等，这可为寻找圆弧形路径提供依据。图形的各种变换，本质上是点的变换，分析问题时，要做到“眼中有点、动中有静”，如例3只需要关注点C关于AE的对称点C′即可，其他的旁枝末节可以忽视，这是教师应培养学生的一种重要的审题与解题能力。

若遇到“来回型路径”，则需要先定性分析，再定量计算，并且结合解析几何、消参数的技巧，在高中解析几何中会系统学习。本文就不详细举例说明。

三、 小结与反思

从以上的例题分析中，笔者认为有些数学问题，将圆隐藏在已知条件里，隐晦地考查圆的有关知识。解题时，需要我们通过分析探索，发现这些隐圆，做到图中无圆，心中有圆，使动点的轨迹一目了然。由于这类问题具有很强的探索性，解题时需要运用动态思维、数形结合、特殊与一般相结合、逻辑推理与合情想象相结合等思想方法。在平时的教学中老师多引导学生善于从复杂的几何图形中抓住图形的本质特征，抽象出常用的数学模型，化繁为简，化难为易，不断提升数学综合思维与解题能力。

参考文献：

[1]邹黎明，周敏峰，邹瑜.巧添“隐圆”求几何最值[J].中学生数学，2018（12）.

[2]段广猛.广猛说题——中考数学压轴题破解之道[M].上海：华东师范大学出版社，2018年7月.

[3]吉宏军.构造隐形圆，妙求几何最值——以一道几何最值问题为例[J].数学教学通讯，2018（29）.

作者简介：

曾立萱，福建省泉州市，福建省泉州七中金山校区。