一题多变 思维提升


摘 要:本文以一道模拟试题为素材,对试题不断进行变式,最终达到一般性结论,这可以拓宽学生的思维,提高学生的解题能力,增强学生学习数学的兴趣,同时体现数学的美和数学的博大精深.
关键词:变式研究;拓展思维;解题能力
通过一题多变的训练可以激发学生把问题多元化,由浅及深.一题多变的目的在于思维的“激发性”与“创造性”,在于让学生从多变中分析出解题的本质,获得思维水平更高的提升.本文通过一道平面向量试题的多变及解析,希望对学生学习解题有所帮助.
1 题目呈现与解析
题目 已知点O是ΔABC的外心,AB=4,AC=2,则AO·(AB+AC)=( ).
A.10 B.9 C.8 D.6
解析 AO·(AB+AC)=AO·AB+AO·AC
=AB·AO·cos∠OAB+AC·AO·cos∠OAC
=12AB2+12AC2=10.
故选A.
2 题目变式与解析
变式1 已知点O是ΔABC的外心,AB=4,AC=2,AC·AB=-2,若AO=xAC+yAB,则x+y=.
解法1 因为AO=xAC+yAB,
所以AO·AC=4x-2y,AO·AB=-2x+16y.
即4x-2y=2,-2x+16y=8.解得x=45,y=35.
故x+y=75.
解法2 如图1建系,A(0,0),C(2,0),B(-1,15).BC的中垂线为y-152=155(x-12).
令x=1时,y=3155,即O(1,3155).
因为AO=xAC+yAB,所以x=45,y=35.
故x+y=75.
变式2 (2018年吉林松原模拟)已知△ABC外接圆的圆心为O,AB=2 3,AC=2 2,∠A为钝角,M是BC边的中点,则AM·AO等于( ).
A.3 B.4 C.5 D.6
解析 因为M是BC边的中点,
所以AM=12(AB+AC).
因为O是△ABC的外接圆的圆心,所以AO·AB=AO·ABcos∠BAO=12AB2=12×(2 3)2=6.
同理可得AO·AC=12|AC|2=12×(2 2)2=4.
所以AM·AO=12(AB+AC)·AO=12AB·AO+12AC·AO=12×(6+4)=5.
故选C.
变式3 (2018年山西四校联考)△ABC的外接圆的圆心为O,半径为1,若AB+AC=2AO,且|OA|=|AC|,则BA在向量BC方向上的投影为( ).
A.32 B.32 C.3 D.-32
解析 △ABC的外接圆的圆心在线段BC的中点O处,因此△ABC是直角三角形,且∠A=π2.
又因为|OA|=|CA|,所以∠C=π3,∠B=π6.
所以AB=3,AC=1.
故BA在BC方向上的投影|BA|cosπ6=32.
故选A.
变式4 (原创题)已知O是ΔABC内一点(包括三边),AB=4,AC=2,AC·AB=-4,
若AO=xAC+yAB,则x+2y的最大值是.
解析 如图3建系, A(0,0),B(4,0),C(-1,3),设O(x0,y0).
因为AO=xAC+yAB,所以x0=-x+4y,y0=3x.①
因为O(x0,y0)是ΔABC内一点(包括三边),
则满足y0+3x0≥0,y0≥0,35(x0-4)+y0≤0.②
将①代入②得x≥0,y≥0,x-1+y≤0.
问题转化为:x,y满足x≥0,y≥0,x-1+y≤0,求x+2y的最大值,画出x,y的可行域.
当x=0y=1时,x+2y取最大值2.
变式5 (2009年安徽卷理)给定两个长度为1的平面向量OA和OB,它们的夹角为120°,如图4所示,点C在以O为圆心的AB上变动,若OC=xOA+yOB,其中x,y∈R,则x+y的最大值是.
解析 设OA与OC的夹角为θ,则OB与OC的夹角为2π3-θ.|OA|=a,|OB|=b,|OC|=c.
所以OC=ca·sin(2π3-θ)sin2π3OA+cb·sinθsin2π3OB
=sin(2π3-θ)32OA+sinθ32OB.
所以x=sin(2π3-θ)32,y=sinθ32.
所以x+y=sin(2π3-θ)32+sinθ32=23(32cosθ+32sinθ)=3sinθ+cosθ=2sin(θ+π6).
因為0≤θ≤2π3,所以π6≤θ+π6≤5π6.
所以12≤sin(θ+π6)≤1.
所以1≤x+y≤2.
所以x+y的最大值是2.
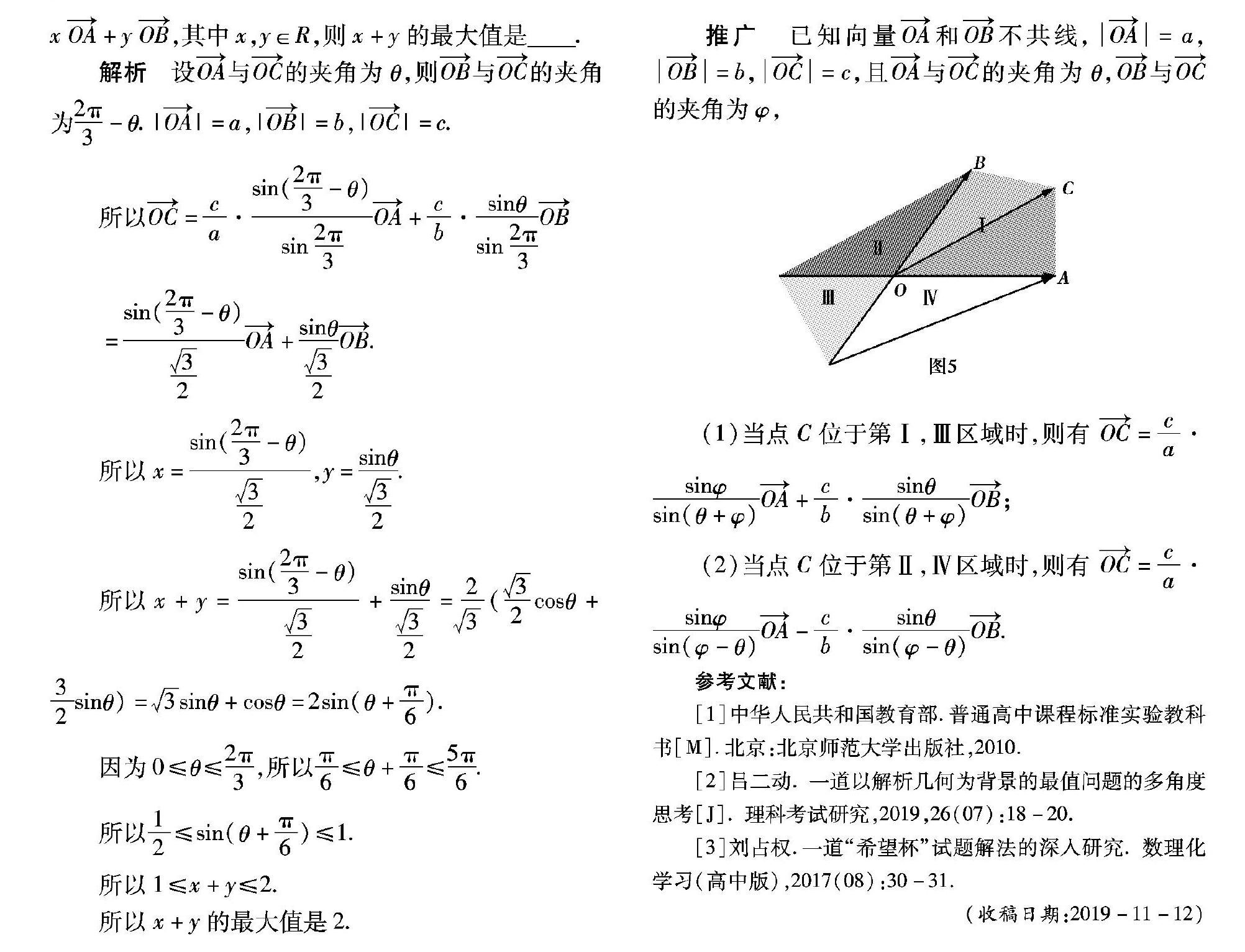
推广 已知向量OA和OB不共线,OA=a,OB=b,OC=c,且OA与OC的夹角为θ,OB与OC的夹角为φ,
(1)当点C位于第Ⅰ,Ⅲ区域时,则有 OC=ca·sinφsin(θ+φ)OA+cb·sinθsin(θ+φ)OB;
(2)当点C位于第Ⅱ,Ⅳ区域时,则有 OC=ca·sinφsin(φ-θ)OA-cb·sinθsin(φ-θ)OB.
参考文献:
[1]中华人民共和国教育部.普通高中课程标准实验教科书[M].北京:北京师范大学出版社,2010.
[2]吕二动. 一道以解析几何为背景的最值问题的多角度思考[J]. 理科考试研究,2019,26(07):18-20.
[3]刘占权.一道“希望杯”试题解法的深入研究. 数理化学习(高中版),2017(08):30-31.
(收稿日期:2019-11-12)

