无参分组大规模变量的多目标算法研究*
朱登京,段倩倩
(上海工程技术大学电子电气工程学院,上海 201600)
1 引言
工程设计问题涉及同时优化多个目标函数,它不同于单目标优化问题,同时优化多个目标函数往往没有唯一解。在没有决策者先验信息的情况下,多目标优化问题MOPs(Multi-objective Optimization Problems)旨在寻找最佳折衷。目前,大规模全局优化问题的求解算法主要分为2种类型:一类是进化算法,对大规模全局优化问题进行整体求解,这种算法的主要代表有群体智能算法、进化计算算法等。另一类是目前取得成果较多的基于分组与局部搜索的算法,即协作型协同进化方法简称 CC(Cooperative Coevolution)算法。CC类算法利用分治的思想,首先将高维问题分解成若干个低维子问题,然后对每个子问题分别进行求解。协作型协同进化框架能将高维的问题分解成多个子问题,因此协作型协同进化算法在大规模变量问题上有更加优秀的表现。
1994年Potter等[1]提出了协同进化算法,通过分解来解决大而复杂的问题,将1个N维问题直接分成N个一维的子问题,再用遗传算法对子问题进行求解。这种方式未考虑到变量之间的关联性。2000年Potter等[2]提出了一种基于子组件体系结构的协同优化算法,将1个N维问题分解成2组N/2维的子问题,该算法虽然在一定程度上考虑到了变量间的关联性,但是如果N很大,每组会产生许多决策变量,导致算法解集质量下降。2005年Shi等[3]将差分分组融入到协同优化算法框架之中,实验表明差分分组的实验结果要优于遗传算法和差分分组本身。随着工程问题变得越来越复杂,相应实际模型的决策变量也更加复杂。因此,在2008年Yang等[4]引入了自适应权重和随机分组的模式,提出了一种能够优化大规模不可分问题的协同进化框架EACC-G(Evolutionary Algorithms Cooperative Coevolution-Group),该方法通过随机分组的方式增大了交互变量分到同一组的概率。随机分组的方式能够有较大的概率使得2个交互变量分到同一组,然而将多个交互变量分到同一组的概率却不够高。2009年Li等[5]提出了差分进化DE(Differential Evolution)的基于分解的多目标优化算法MOEA/D(Multi-Objective Evolutionary Algorithm based on Decomposition)新版本,实验结果表明MOEA/D-DE的性能明显优于NSGA-II。这表明基于分解的多目标进化算法在处理复杂的PS(Pareto Set)形状时能够提升算法解集质量。2014年Omidvar等[6]提出了一种基于变量交互性来划分变量的方法,此方法通过2个变量之间差值的大小来判断变量间是否交互;2个决策变量的交互系数大于某个设定好的阈值,才会将这2个决策变量分到同一组。该方法比随机分组的方式具有更强的鲁棒性。2016年Cheng等[7]提出了一种处理不规则PFs的参考向量再生策略算法RVEA(Reference Vector-guided Evolutionary Algorithm),该算法采用了一种称为角度惩罚距离的尺度化方法来平衡高维目标空间中解的收敛性和多样性。对于多目标问题来说,决策变量的规模越大,变量间的关联性也随之增大。根据决策变量间的交互性对变量进行分组,能够将高维的问题分解为简单的低维问题,从而能够更大程度上保证解集的质量。
本文将协同优化与MOEA/D[8]相结合,并对基于变量交互性分组的方式进行改进,提出了一种无参交互变量分组的多目标优化算法MOEA/DGWP(Multi-Objective Evolutionary Algorithm based on Decomposition-Group Without Parameters)。此算法的主要优点是通过自动计算其阈值参数(ε),能够更加精确地识别出决策变量之间的交互性,提高变量分组的精确性。最后经过实验分析,MOEA/DGWP算法产生的解集具有更好的多样性和收敛性。
2 背景
2.1 多目标问题的定义
一个具有n个决策变量,m个目标变量的多目标优化问题(MOPs)描述为[9]:
(1)
其中,Ω是决策空间,F:Ω→Rm包括m个实值目标函数值,Rm称为目标空间。x是在可行域Ω的决策向量。
令u,v∈Rm,如果对于任意的的i,ui≥vi,当且仅当对于任意的i∈{1,…,m},ui≥vi并且至少存在1个下标j∈{1,…,m},uj>vj,那么称为u支配v(表示成uv)。如果在决策空间中,没有1个点x∈Ω使得F(x)F(x*),那么将x*∈Ω称为Pareto最优解。换句话说,对于Pareto最优点在某一个目标函数上的提高,都会造成至少1个其余目标函数的退化。所有Pareto最优解的集合称为Pareto集合(PS),所有最优向量的集合被称为Pareto前沿PF(Pareto Front)。
2.2 基于分解的多目标进化算法(MOEA/D)框架
基于分解的多目标进化算法的主要思想是使用一个聚合函数将多目标优化问题转化为一系列单目标优化子问题,然后利用一定数量相邻问题的信息,采用进化算法对这些子问题同时进行优化。
MOEA/D算法在每一代中需要保存如下信息:
N个种群{x1,…,xN},其中xi是第i个子问题的当前解;
FV1,…,FVN,其中FVi为xi的F值,即FVi=F(xi),1=1,2,…,N;
z=(z1,…,zm)T,其中zi为目前为止目标函数fi的最优解;
用于存放搜索过程中搜寻到的非支配解的外部种群库EP(External Population)。
MOEA/D算法具体步骤如算法1所示。
算法1 MOEA/D
输入 需要被优化的多目标问题MOP;
N:子问题的个数;
N个均匀分布的权重向量λ1,…,λN;
T:权重向量的相邻向量的个数;
算法终止条件,例如,最大迭代次数、算法最大运行时间等。
输出EP。
步骤1 初始化各项参数:
步骤1.1 使得EP为空集;
步骤1.2 计算任意2个权重向量之间的欧氏距离,再根据欧氏距离来为每个权重向量选出T个权重向量作为它的邻居。设B(i)={i1,…,iT},i=1,…,N。其中λi1,…,λiT为λi的T个最近的权重向量;
步骤1.3 随机产1个初始种群x1,…,xN,令FVi=F(xi)。
步骤1.4 初始化参考点z=(z1,…,zm)T。
步骤2 更新:
Fori=1,…,Ndo
步骤2.1 繁殖操作:从B(i)中随机选择2个索引k,l,再通过遗传算子从xk和xl中产生新的解y;
步骤2.2 修复/改进:使用基于特定问题的启发式对解y修复或改进为y′;
步骤2.3 更新参考点z:如果zj 步骤2.4 更新邻域解:对于每个索引j∈B(i),如果gte(y′|λj,z)≤gte(xj|λj,z),则令xj=y′,FVj=F(y′); 步骤2.5 更新外部种群EP:移除EP中所有被F(y′)支配的向量,如果EP中没有被F(y′)支配的向量,则将F(y′)添加到外部种群EP中。 步骤3 终止:如果满足终止条件,例如达到最大迭代次数、最长运行时间等,则停止算法并输出外部种群EP;否则,返回步骤2。 在生物学中,如果存在2个基因同时对某个生物的特性产生影响,那么称这2个基因之间是相似的。在遗传算法中,当一个变量的改变导致另外一个变量也改变,那么称这2个变量为交互变量。反之,一个变量的改变不会影响另外一个变量,这2个变量称为非交互变量。函数的可分性和不可分离性定义如下: 定义1 函数f(x1,…,xn)是可分的当且仅当[10]: arg minx1,…,xnf(x1,…,xn)=(arg minx1,f(x1,…)…,arg minxnf(…,xn)) (2) 换句话说,如果可以通过一次优化一个维度来找到函数的全局最优值,而不管其他维度的值如何,则该函数被称为可分离函数;否则就是不可分离函数。 定理1 如果f(x)是连续可分离函数,那么对于x中的任意1个分量xp有: (3) 其中,f(xi)为f(x)的任意一个分函数。 证明 因为f(x)是连续可分函数,所以得到: (4) 其中x1,…,xm是互斥的决策向量。因此: (5) 所以: (6) 证明完毕。 定理2 当f(x)是连续可分函数时,若∀a,b1≠b2,δ≠0使得下式成立,则xp和xq为交互变量。 Δδ,xp[f](x)|xp=a,xq=b1≠Δδ,xp[f](x)|xp=a,xq=b2 (7) 其中: Δδ,xp[f](x)=f(…,xp+δ,…)-f(…,xp,…) (8) 定理2说明,给定一个连续可分离函数f(x),如果用任意2个不同值xp和xq对式(8)进行求值,得到不同的结果,那么2个变量xp和xq是交互变量。 证明 由定理1可知,当xp不是xi的分量时: ∀b1≠b2 Δδ,xp[f](x)|xp=a,xq=b1=Δδ,xp[f](x)|xp=a,xq=b2 ∀a,b1≠b2,δ∈R,δ≠0 证明完毕。 为了易于描述,本文接下来将式(7)的左边使用Δ左表示,右边用Δ右表示。通过式(7)可以得出Δ左≠Δ右⟹|Δ左-Δ右|≠0。然而由于在计算机中的浮点精度有限,这种利用等式检查交互变量的方式是不可行的。因此,现在的检查方式是将等式转化为不等式,通过引入1个参数来提高检测的敏感性:λ=|Δ左-Δ右|>ε,ε通常是1个很小的数。如果λ大于ε,那么就认为2个变量之间是交互的,便将变量分在同一组。如果λ小于ε,那么就认为2个变量之间不存在交互性。 本文通过估计舍入误差的最大下界einf和最小上界esup来得到1个阈值。如果λ=|Δ左-Δ右|>esup,则认为2个变量之间是交互的;如果λ=|Δ左-Δ右| 目前绝大多数的个人计算机和工作站采用的是IEEE754标准,在使用有限精度的计算机存储单元来表示无限精度的实数时,舍入误差的产生是不可避免的。 在IEEE754标准中,浮点数集合(包括0)是1个有限的集合,记为F。集合F中的非零浮点数均匀地分布在[-M,-g]和[g,M]上,其中g和M是机器能表示的最小和最大正浮点数。 对于实数x,对应机器上的浮点数记为fl(x)。如果x=0,那么fl(x)取0。如果g≤|x|≤M,采用舍入法,取fl(x)为F中最接近x的数。若|x| fl(x)=x(1+δ) (9) (10) 除了上述提到的舍入误差以外,计算机上基本算术运算也将产生舍入误差。在IEEE标准中规定了x⊕y=fl(x+y),其中⊕意为浮点求和运算。换句话说,保证了2个数字的浮点和等于与2个数字的实际和最近的浮点数。 定理4 若给定一系列满足IEEE754标准的浮点数,则|δi|<μM,可以得到[12]: (11) 为方便描述本文将nμM/(1-nμM)用γn代替。 定理4可以用于在任何计算中找出累积算术误差的上界。本文利用定理4给出了计算误差的一个合理的上、下界。为了估计舍入误差大小的最大下界,假定f(x)的计算是无误差的,错误的唯一来源是在计算λ=|Δ左-Δ右|时产生的,因此: fl(Δ左)=f(x)⊖f(x′)= (f(x)-f(x′))(1+δ1)=Δ左(1+δ1) fl(Δ右)=f(y)⊖f(y′)= (f(y)-f(y′))(1+δ1)=Δ右(1+δ2) fl(λ)=|fl(Δ左)⊖fl(Δ右)|= |fl(Δ左)-fl(Δ右)|(1+δ3)= |f(x)(1+δ1)(1+δ3)-f(x′)(1+δ1)(1+δ3)- f(y)(1+δ2)(1+δ3)+f(y′)(1+δ2)(1+δ3)| 通过上面的推导可以看出n=2,因此通过定理4可以得到下式: |λ-fl(λ)|≤γ2|(f(x)-f(x′))- (f(y)-f(y′))|=γ2|(f(x)+ f(y′))-(f(y)+f(x′))|≤γ2· max{(f(x)+f(y′)),(f(y)+f(x′))} 即舍入误差的最大下界einf=γ2·max{(f(x)+f(y′)),(f(y)+f(x′))}。 (12) (13) 通过估计最小上界esup和最大下界einf,可以识别可靠的λ值。所有λ大于esup的值将被视为真正的非零值(交互变量),所有小于einf的值被视为真正的零值(分离变量)。最后,对于(einf,esup)范围内的值,使用下面的边界加权平均值设置阈值: (14) 其中η0是通过λ=|Δ左-Δ右|计算得的值中大于einf的个数,η1是通过λ=|Δ左-Δ右|计算得的值中小于esup的个数。 算法2 无参变量分组算法 步骤1 利用定理4计算出舍入误差的最大下界einf和最小上界esup,再利用式(14)计算出ε的值。 步骤2 从种群中随机选取2个不同变量i和j,计算λ=|Δ左-Δ右|的值并作出如下判断:若λ大于esup,则认为变量i和j是交互变量,将它们放入同一组中;若λ小于einf,则认为变量i和j为可分离变量;若λ∈[einf,esup],则将λ与ε比较,大于ε便认为i和j是交互变量,否则为可分离变量。 步骤3 重复上述步骤2识别其它所有变量是否与变量i交互,若存在交互,则放在同一组中。然后与第i+1个变量进行交互性检测和分组,直到所有的决策变量都被检测完为止。 本文提出的无参变量分组的分解多目标优化算法(MOEA/DGWP),不仅将协同优化算法引入到MOEA/D算法中,还对交互变量识别、分组方式进行改进。算法通过将交互变量尽可能地分到同一组中,减少分组后子问题之间的相互依赖,从而能够有效地提高解集的质量。该算法步骤如算法3所示。 算法3 MOEA/DGWP 输入:MOP;停止准则;MOEA/D中考虑的子问题的数量;1组均匀的权重向量;每个权向量的邻居权向量的个数。 输出:EP。 步骤1 初始化和设置各项参数大小; 步骤2 对种群进行交叉变异操作产生子种群; 步骤3 通过无参变量分组算法对决策变量进行分组; 步骤4 使用MOEA/D算法对步骤3所产生的交互变量分组后产生的子问题进行求解,得到局部最优解; 步骤5 将步骤4产生的局部最优解合并到全局最优解; 步骤6 若满足终止条件,输出EP;否则,更新每个子问题权重系数,返回步骤3。 在MOEA/DGWP算法中,将交互变量分组和基于分解的多目标优化进化算法进行协同来优化多目标问题。通过计算舍入误差的方式来提高分组的精确性,将大规模变量问题分解为低维问题来提高算法解集的质量。 为了测试本文所提出的算法处理大规模变量多目标问题的性能,本文使用测试多目标问题的测试函数UF1和UF2。仿真实验中所有种群大小N统一设置为100,迭代次数均为1 000 000次。为降低实验的偶然性,各算法将各多目标问题测试30次。决策变量维数为100,200。并且与MOEA/D、RVEA、MOEA/D-DE多目标优化算法进行比较。 从图1~图4中可以看出,随着决策变量的增加,算法MOEA/D、RVEA和MOEA/D-DE的解集质量变得越来越差。MOEA/DGWP的解集质量在不同测试函数和不同决策变量维数下均要优于所测试的其它多目标优化算法的。 Figure 1 PF of test function UF1 with different algorithms under 100 variables图1 100个决策变量下各算法测试函数UF1的Pareto前沿 Figure 2 PF of test function UF1 with different algorithms under 200 variables图2 200个决策变量下各算法测试函数UF1的Pareto前沿 Figure 3 PF of test function UF2 with different algorithms under 100 variables图3 100个决策变量下各算法测试函数UF2的Pareto前沿 Figure 4 PF of test function UF2 with different algorithms under 200 variables图4 200个决策变量下各算法测试函数UF2的Pareto前沿 本文使用综合评价指标反世代距离(IGD)来衡量算法的收敛性和分布性。反世代距离采用Pareto最优解集PFture中的个体到算法所求的非支配解集PFknown的平均距离表示[13]。计算公式为: (15) 其中,P是优化算法求得的解集,P*是从PF上采样的一组均匀分布的参考点,dis(x,y)表示参考集P中点x到参考集P中点y之间的欧几里得距离。IGD的值越小,就意味着算法的综合性能就越好。 仿真实验得到的结果如表1所示。表1统计了5个算法在不同决策变量个数下求解测试函数UF1和UF2的IGD均值和均方差(括号内为均方差),D表示决策变量个数。从表1可以看出,MOEA/DWPG的IGD均值和均方差都要低于MOEA/D和其它先进算法的。IGD的均值越低表示算法的收敛性和分布性能越好。IGD的均方差表示了IGD的离散程度,均方差值越低,则代表每次运行结果差异性越低,结果更加稳定可靠。从实验结果可以看出,基于无参数交互变量分组的方法能够有效地将交互变量分到同一组,MOEA/DGWP在求解测试问题UF1和UF2时所获得的解集质量更高,有着比MOEA/D和其它先进算法更好的收敛性和分布性。 本文提出的基于无参数交互变量分组的多目标进化算法(MOEA/DGWP),将协同优化与基于分解的多目标优化算法相结合,设计了一种新的分组方式,该分组方式通过计算舍入误差提高了变量分组的精确性。通过与MOEA/D和其它先进算法的比较表明,MOEA/DGWP算法在求解大规模变量优化问题时所获得的解集质量更高。 Table 1 IGD standard values and mean square error表1 IGD的标准值和均方差2.3 交互变量的定义
3 不含参数的交互变量分组的多目标优化算法
3.1 不含参数的分组策略
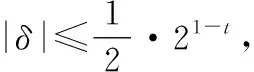



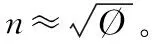


3.2 不含参数的交互变量分组的多目标优化算法框架
4 实验研究
4.1 测试问题及参数设置
4.2 实验结果

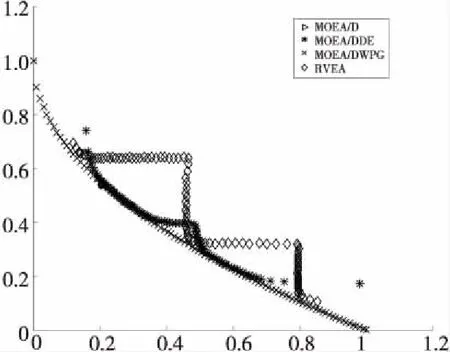


4.3 算法评价指标
5 结束语


