张量化扩展变换的低秩图像修复算法
诸葛燕1,徐宏辉,郑建炜
(1.浙江经济职业技术学院 数字信息技术学院,浙江 杭州 310018;2.浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
图像修复[1](Image inpainting),又称图像补全,不仅可以填充图像丢失的像素,而且可以移除图像中不需要的物体或文字,其工作原理为利用周围已知的信息即先验知识或者先验假设,建立数学模型并寻找最优化准则求解缺失部分的信息。与此同时,修复过程中要保留图像的细节以及整体结构的连贯性,最终完成图像修复。传统基于结构扩散[2]的方法以像素为单位沿着等照度线由外到内依次进行迭代修复,通过偏微分方程(Partial different equation,PDE)将图像中已知的结构和颜色等信息扩散到待填补区域,但该方法只能应用于较小区域的修复,例如划痕、文字等破损。针对较大区域的图像修复,张桂梅等[3]提出了基于纹理的修复技术,根据等照度线驱动采样过程,通过搜索最佳相似匹配块,将其纹理复制到目标区域,此方法通过平衡优先权函数中置信项和数据项来同时处理图像中的结构信息和纹理信息。张剑华等[4]提出了一种基于目标形状特征和纹理特征的迭代配准的方法,并运用在医学诊疗中。近年来,矩阵逼近[5]问题成为图像处理领域和计算机视觉领域的研究热点,其核心思想是利用数据矩阵的某些结构信息来恢复丢失的数据元素。如冯雅莉等[6]将图像修复问题建模为矩阵填充问题。然而,矩阵秩函数[7]不是一个凸函数,为解决该问题,高成英等[8]提出了基于稀疏表示的图像修复,Chen等[9]将自然图像编码为纯四元数矩阵,提出了一个新的低秩四元数近似模型来实现修复。Geng等[10]提出了一种基于联合截断核范数和组稀疏表示的图像修复算法。Jin等[11]利用Hankel矩阵的低秩性,将Hankel卷积结构矩阵移植于自然图像的修复应用。金燕等[12]提出一种总变分和小波框架双正则化模型对图像进行修复。综上所述,在图像处理领域,图像修复可以归结为矩阵补全问题,这方面已经有了很好的研究。但随着现在科学技术的发展,人们现在存储、处理和分析的数据规模更大、维度更高、结构更复杂,仍采用矩阵补全算法来处理可能会付出大量的计算代价,因此近年来很多学者提出了低秩张量补全的方法来对图像进行修复。Liu等[13]提出了简单低秩张量补全算法对图像缺失的像素进行填充。Lu等[14]重新定义了张量谱范数、张量核范数和张量平均秩,提出了新型的张量分解模型。Liu等[15]提出了新的低秩光滑张量树逼近张量补全模型,对全局数据结构采用张量树秩最小化,对局部结构采用全变分最小化。受文献[11,15]启发,笔者把数据延伸到高维张量空间中,并将张量Hankel化,使其具备低秩性,再对变换后的张量进行缺失数据补全。具体而言,现存优化算法将矩阵结构化技术运用于填充问题,在自然图像修复、磁共振图超解析[16]等领域,并获得了成功。矩阵结构具有低秩性、光滑性,张量中同样具备矩阵的一些性质。因此,笔者应用Hankel化技术,深入挖掘张量的低秩性,并在Tucker分解[17]的基础上,提出辅助张量分解方法,从而简化分解过程的复杂度,提升优化过程的收敛性。
1 Hankel张量化的低秩图像修复算法
1.1 符号表示
所采用的向量由粗体小写字母α∈RI表示,矩阵用粗体大写字母A∈RI×J表示,高阶(N≥3)张量用粗体书写字母A∈RI1×I2×…×IN表示,向量的第i个元素表示为ai,矩阵的第(i,j)项用aij来表示,N阶张量A的第(i1,i2,…,iN)个元素用ai1i2…iN表示。张量是一个多维数组或多维矩阵。张量的阶(order)称为维数或模。常见的自然图像可视为三维张量。矩阵的行和列在解决矩阵补全问题发挥着重要作用。类似于矩阵的行和列,在张量中我们称其为纤维。三阶张量A有行纤维、列纤维和管纤维,分别表示为a:jk,ai:k,aij:,如图1所示。

图1 三阶张量的三种纤维Fig.1 Three different types of any 3-order tensor
除张量纤维外,和矩阵不同的还有张量切片,其实际上是二维子阵列。例如三阶张量A有水平切面、侧面切面和正面切面三种切面,分别表示为ai::,a:j:,a::k,如图2所示。

图2 三阶张量的三种切片Fig.2 Three different slices of any 3-order tensor
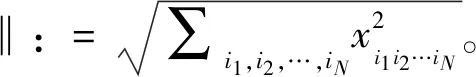
1.2 Hankel化操作
本节主要回顾Hankel化操作[11],首先针对向量实施Hankel化操作,其向量可以视为一个时间序列信号v,其具体形式为
v=(v1,v2,…vL)T∈RL
(1)
定义矩阵束τ,则可将信号v进行结构化变换,使其变化为Hankel矩阵。例如当矩阵束τ=3时,可将时间序列信号v=(1,2,3,4,5,6,7)THankel化为
(2)
根据式(2)的操作,时间序列信号v在矩阵束τ下Hankel化为
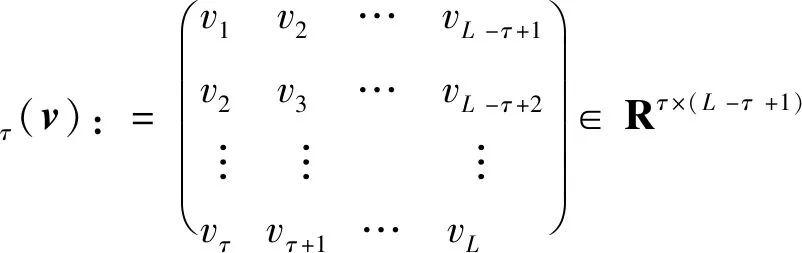
(3)

vec(Hτ(v))=Sv
(4)

式(3)可以重新表示为
Hτ(v)=fold(L,τ)(Sv)
(5)
式中fold(L,τ)是将向量转变成Hankel矩阵的算子,其形式为fold(L,τ):Rτ(L-τ+1)→Rτ×(L-τ+1)。
接下来介绍逆Hankel化。由前文可知,正变换通过构造复制矩阵和折叠操作将向量转变为Hankel矩阵,因此逆变换也可以分解为相对应的反变换:矢量化操作和Moore-Penrose广义逆[19],即Hankel矩阵的逆变换为
(6)
式中VH为Hankel化之后的结构矩阵,S°:=(STS)-1ST。
1.3 Hankel技术的有效性
在信号处理中,Hankel矩阵的低秩特性[11]被广泛用于信号线性定常系统的建模。例如,Li等[20]提出了一种基于低秩Hankel近似的阻尼正弦信号建模方法。受文献[20]的启发,笔者把所提的Hankel技术应用在信号重构方面以验证所提Hankel技术的有效性,结果如图3所示。图3为在矩阵束τ=20的约束下构建的Hankel矩阵重建含噪信号x(t)的实验图,其中图3(a)为原始完整信号,图3(b)为受破坏后的信号,图3(c)为修复后的信号。从图3(b)可以看出信号已经被严重损坏,不能被正常识别,经过Hankel矩阵化技术修复后(图3c)接近于原始信号,通过上述分析,笔者在矩阵束约束下所构建的Hankel化技术可以完好地将受损信号重构。
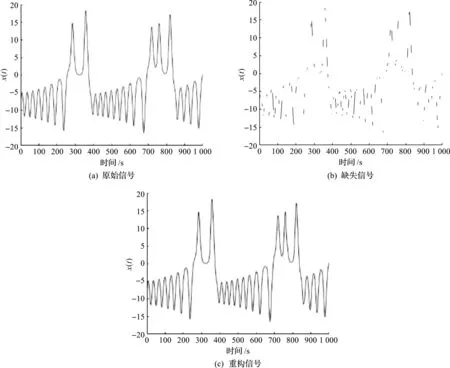
图3 Hankel矩阵重构含噪信号示意图Fig.3 Schematic diagram of noisy signal reconstruction
1.4 张量的Hankel化
前面几节介绍了向量的Hankel变换,本节将主要介绍对张量进行Hankel操作。类似于向量Hankel折叠化是线性复制和折叠操作的结合,张量中的Hankel折叠化操作也为多维线性复制和多维的折叠操作。一个N阶张量X∈RI1×I2×…×IN的Hankel化可表示为
Hτ(X)=fold(L,τ)(X×1S1…NSN)
(7)
式中fold(I,τ)表示Rτ1(I1-τ1+1)×…×τN(IN-τN+1)→Rτ1×(I1-τ1+1)×…×τN×(IN-τN+1)。通过fold(I,τ)可将输入的N阶张量构造成一个2N阶张量,例如矩阵L∈R5×8可在重复矩阵S∈R9×5的作用下构成结构矩阵,具体操作为
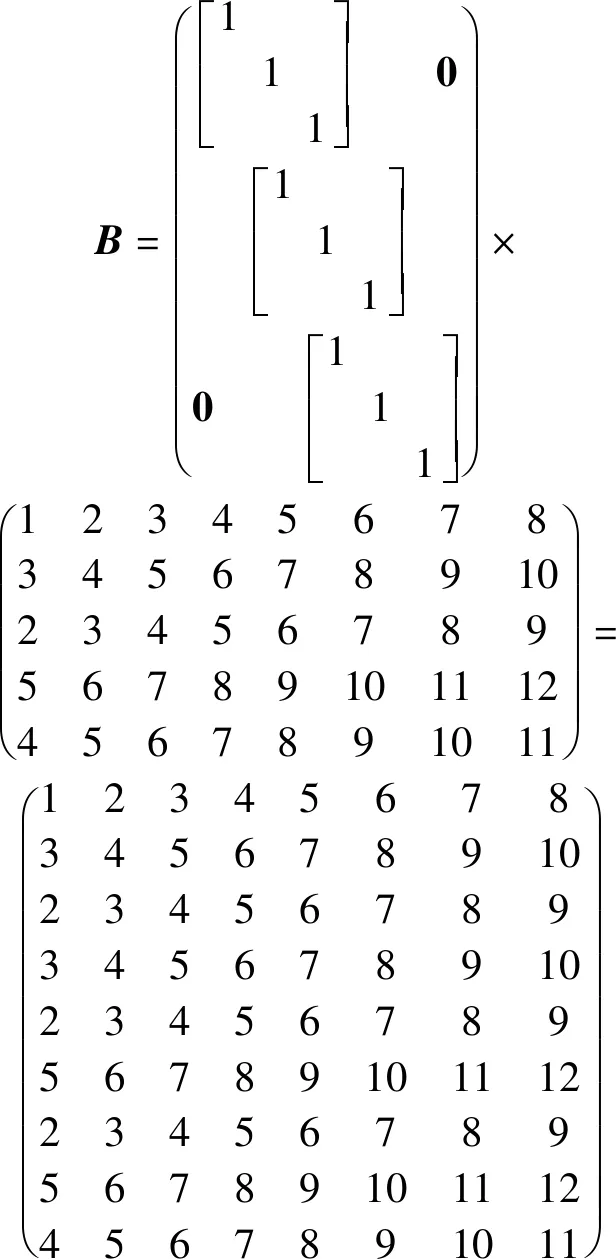
(8)
式中B的每一列依照前文1.2所述在矩阵束τ1的约束下可构成Hankel矩阵,例如当矩阵束τ1为3时,B的第一列可Hankel化为
(9)
因此B在矩阵束的约束下构成了3×3×8的Hankel张量,其一般矩阵X∈Rm×n构造方法如图4(a)所示。式(8)展示了一维的张量Hankel化,B可继续在重复矩阵S的作用下进行多维Hankel化,具体形式为

(10)
式(10)的每一行如B的每一列,也可在矩阵束τ2的约束下构建成Hankel矩阵,经过式(8)与式(10)的操作可构建出本文所需的多维Hankel张量,构建流程如图4(b)所示。

图4 张量Hankel折叠化过程Fig.4 Tensor Hankel folding process
类似地,Hankel张量XH的逆Hankel化可表示为

(11)
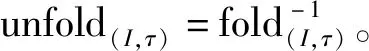
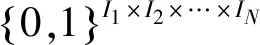
TH=H(T)∈RJ1×J2×…×JM
(12)
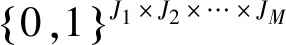
(13)
其中M≥N。综上,提出一种基于Hankel化的张量补全图像修复算法(Low rank tensor model based on Hankelization, LRTH),具体形式为

(14)
式中Rm≤Jm(∀m)。
2 模型求解
由于输入的缺失数据为Hankel折叠后的高阶张量,因此需要对式(14)进行张量分解得到TH的低秩近似。常用的张量分解方式有CP分解[21]和Tucker分解。当针对数据完整张量使用Tucker分解时,可以使用交替最小二乘(Alternating least squares, ALS)[22]获得其驻点。而针对数据丢失的张量,近年来多采用梯度下降法[23],但其优化通常是缓慢收敛的。笔者在Tucker分解的基础上,提出使用一种基于辅助函数的方法对有缺失元素的张量进行分解,提升了优化过程的收敛性。首先,定义原始损失函数g(θ)和辅助函数w(θ|θ′),具体形式为
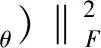
(15)


w(θ|θ)=g(θ)
(16)
w(θ|θ′)≥g(θ)(θ≠θ′)

g(θk):=w(θk|θk)≥
w(θk+1|θk)≥g(θk+1)
(17)
由式(17)可知,损失函数是单调递减的。值得注意的是,θk+1只有满足w(θk|θk)≥g(θk+1|θk),式(17)才具有非单调性。因此,可将辅助函数重新表示为

(18)
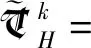
在实际应用中,该算法包括以下两个步骤。
步骤1计算辅助张量,即
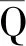
(19)

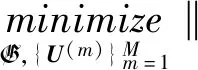
s.t.U(m)TU(m)=IRm(∀m)
(20)
所提的辅助Tucker分解算法总结在算法1中,其中只以U(m)和G的一次循环更新为例。
算法1基于Tucker分解的张量补全
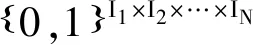
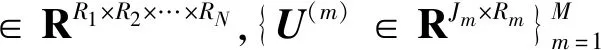
3)Xθ←G×{U}
5) 对m=1,…,M依次进行步骤6,7
6)Y←Z×-m{UT}
7)Um←Rm
8)G←Z×{UT}
9) 收敛结束
10) 输出:G,U(1),…,U(M)
最后通过Tucker分解的逆Hankel操作得到最终合成张量,即

(21)
3 实验分析
为验证所提Hankel张量化方法应用在图像修复的有效性,实验图像选择标准库中具备不同纹理信息的Lena,house,peppers和facad 4 张图像(图5),并与其他修复模型进行实验对比。对比算法由最近提出的5种修复模型组成,包括SILRTC[13],ALOHA[11],LRTV[15],TNN[10],TRPCA[14]。修复结果的主观评判主要采用人眼观察,笔者采集了30 名不同年龄段(10~20,20~30,30~40各10 名),不同性别(男、女各5 人)对于不同算法图像修复效果的评价数据,统计表格如表1所示,客观评判使用峰值信噪比(Peak signal to noise ration,PSNR)[24]来进行数据评判。PSNR定义为
(22)

图5 实验图像Fig.5 Experimental images
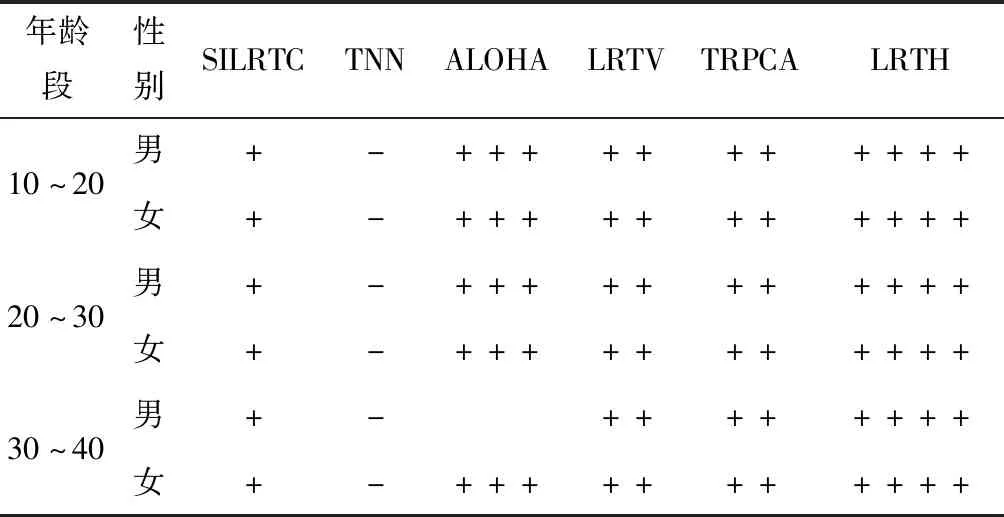
表1 不同人群对于实验效果的统计表Table 1 Statistical table of experimental effects of different people
注:1. “+”代表积极评价,“+”越多即为修复效果越好。
2. “-”代表负面评价,“-”越多即为修复效果越差。
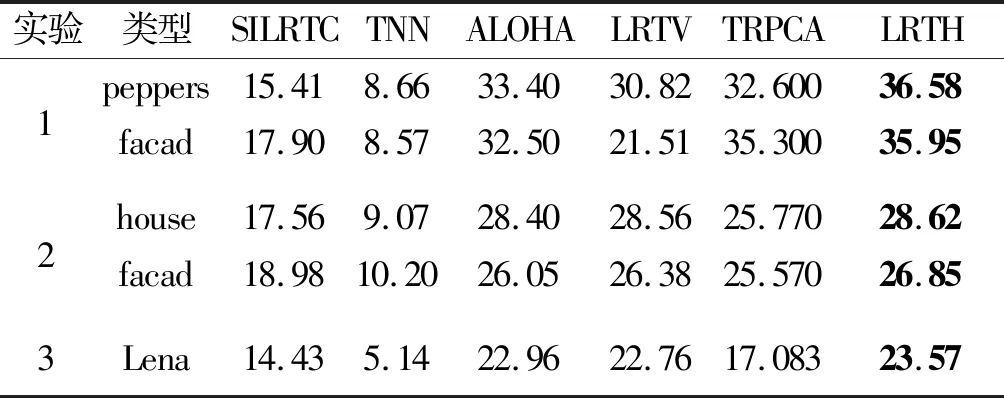
表2 各组实验PSNR值Table 2 PSNR value
为衡量各算法在不同丢失情况的实施效果,分别采用3种元素丢失方式进行实验。实验1:对peppers和facad实施少量的条状丢失;实验2:在house和facad图像加入大量的条状丢失;实验3:使Lena图像中丢失95%的像素值。
针对实验1,表2和图6,7分别显示了本实验的数值评价结果和可视化对比结果,其中表2中粗体字表明最优数值指标。

图6 facad少量条状像素缺失修复实验图Fig.6 A small number of strip pixel missing experimental diagram
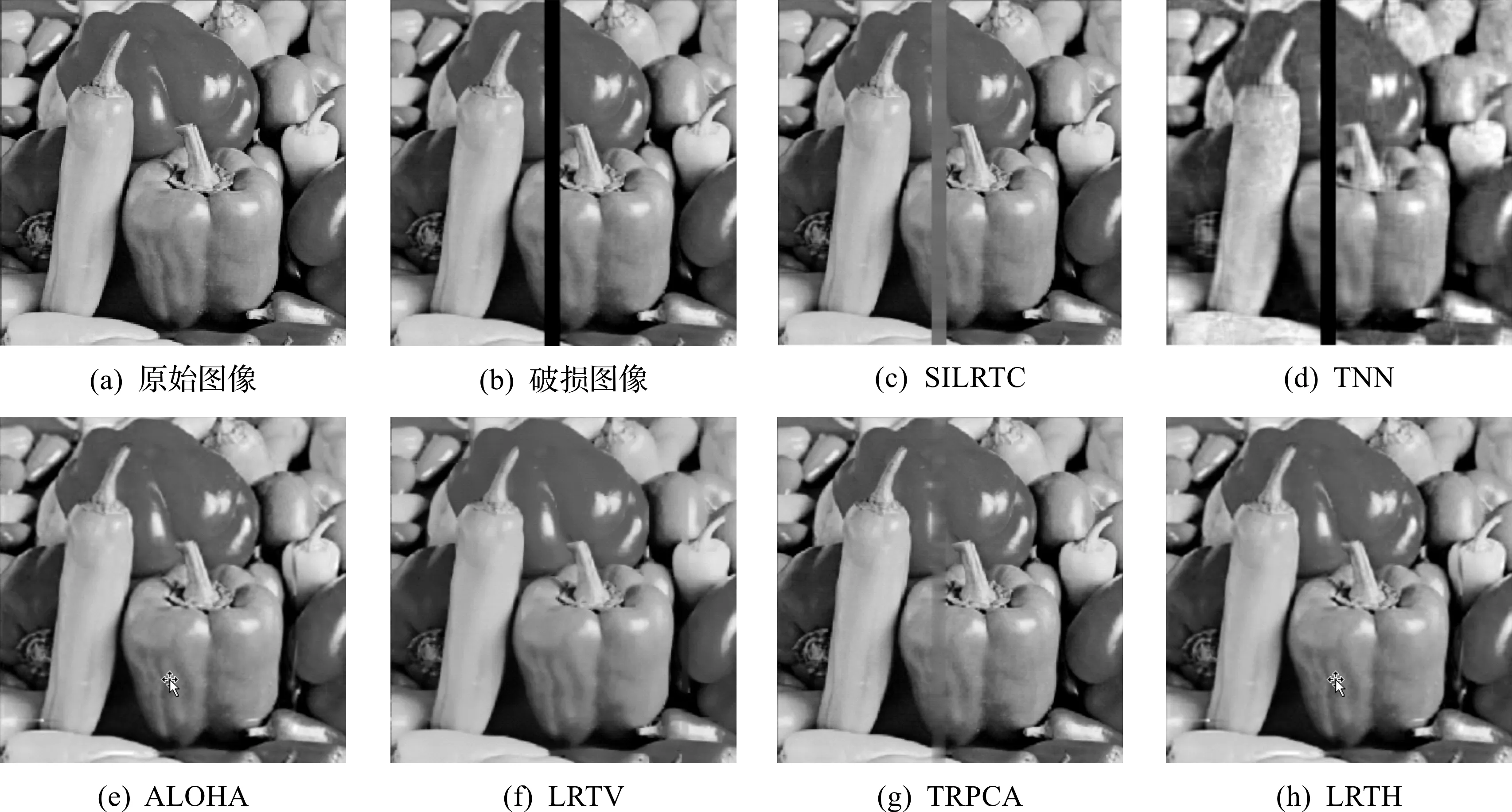
图7 peppers少量条状像素缺失修复实验图Fig.7 A small number of strip pixel missing experiment diagram
从图6可见:TNN和LRTV对于图像facad的条状缺失基本没有修复能力;SILRTC能够将条状缺失像素填充,但其修补后留下了较明显的痕迹;ALOHA和TRPCA整体上能够修补缺失的条状像素,但图像细节方面还是存在着缺陷;LRTH恢复图在视觉上基本与原输入样本一致,修复效果显著。从图7可以看出:TNN的修复效果仍为最差;SILRTC与TRPCA修复之后的图像存着较为明显的痕迹;从视觉上来看,ALOHA、LRTV和LRTH都能较好地进行图像填充,但从表2来看,LRTH的PSNR值较次优的ALOHA领先3.18 dB。从实验1的两组实验可得,LRTH对于少量条状像素缺失的修复能力优于其他算法。
针对实验2,表2和图8~9分别显示了本实验的数值评价结果和可视化对比结果,其中表2中粗体字表明最优数值指标。

图8 facad大量条状像素缺失修复实验图Fig.8 A large number of strip pixel missing experiment diagram

图9 House大量条状像素缺失修复实验图Fig.9 A large number of strip pixel missing experiment diagram
从图8以及表2可以看出:SILRTC和TNN的表现较弱,所恢复的图像存在明显的痕迹。TRPCA存在着少量的痕迹,LRTV虽然修复痕迹不是很明显,但其细节信息和边缘信息没有得到很好地处理,ALOHA和LRTH能够较好地填充大量条状像素缺失区域,从表2看出,LRTH略优于ALOHA。类似于图8的修复效果,在图9中,SILRTC,TNN,TRPCA的修复效果较弱;ALOHA,LRTV和LRTH能够较好地还原,从数据上来看,LRTH稍稍优于前两种算法。
针对实验3,表2和图10分别显示了本实验的数值评价结果和可视化对比结果,其中表2中粗体字表明最优数值指标。

图10 95%像素点缺失的Lena修复实验图Fig.10 95% pixel missing experiment diagram
从图10看出:TNN的修复效果最差,其可视化结果已经无法辨认出图像信息;SILRTC能够修复出轮廓,但具体细节依旧无法辨认且颜色还原度较差;TRPCA较好地还原了整体轮廓,但其与原图的色差较大;ALOHA和LRTV较于前三者能够较好地恢复轮廓和颜色信息,但其细节、纹理没有得到很好地处理;笔者算法在图像的细节方面表现更优,能够很好地保留边缘、细节信息,从表2数值评价角度,LRTH的PSNR值较次优结果领先0.61 dB。
综上所述,在少量条状像素缺失的情况下,LRTH修复效果远远优于其他算法;当条状像素缺失较多时,无论在视觉方面还是数据方面,笔者算法优于其他算法,并且能够较好地还原边缘、细节信息。在像素点丢失较多的情况下,笔者算法依然能够还原出轮廓清晰、细节信息完好的图像。总体而言,笔者算法对图像的综合修复效果占优。
4 结 论
受低秩Hankel矩阵方法启发,笔者把Hankel化技术扩展应用至张量领域中。考虑到矩阵的低秩性、光滑性同样存在于张量中,首先将数据嵌入到高维张量中,经过多维线性复制和多维的折叠线性操作将张量Hankel化;其次通过笔者提出的基于辅助函数的Tucker分解对低秩张量进行近似求解,具有良好的收敛性;最后将求得的多维张量逆Hankel化至原始张量,并恢复至原始数据尺寸。实验结果表明,笔者算法在可视化效果和定量评价分析上都优于其他算法。通过实际应用过程发现,Hankel化之后的张量维度较大,笔者算法的实现效率有待进一步改性。因此,后续工作将重点针该问题展开,提升算法的扩展应用能力。

