全景思维在解题中的应用

叶鋆纯 王向东

【摘要】解决问题是数学学习的核心活动，而解决数学问题需要有全景性的思维来支撑.当前，由经验性知识转向实证性知识已成为国内外研究数学问题解决的新趋势.[1]本文通过介绍全景思维的定义、特征及研究现状，阐述了全景思维在解决数学问题中的应用范围、应用步骤及一些方法技巧，为拓展学生解题思维给出了相应的探讨.

【关键词】全景思维;解题;应用

一、全景思维的提出及其发展

全景思维是指在给定的数学问题情境下，能尽可能地认识和再现问题的本质和全貌，多层次全方位的获取相关信息，与已有知识经验充分联结，最终寻得问题突破的一种思维方法.它能对已有经验进行重组和改造，且能对解题过程中的行为活动进行自我监控.全景思维具有个体性、系统性、发散性和创造性等特征.它对学习者已有的知识经验不断进行融会贯通，梳理修正，最终形成越来越完备的认知结构从而影响学习者今后的学习.用波利亚的话说，学习从行动和感受开始，再从这里上升到语言和概念，最终形成该有的心理习惯.[2]目前，已有不少学者对数学知识表征、知识体系和解题策略等方面进行相当多的研究，但较少有全面系统的解题思维的研究.

罗增儒在《数学解题学引论》一书中对波利亚怎么解题的思维进行研究[3]，其概括为四个层面：一是程序化的解题系统;二是启发式的过程分析;三是开放式的念头诱发;四是探索性的问题转换.本文提出的全景思维具体表现同样为四个层面：一是能在脑海中全景建立数学知识结构;二是全面深刻剖析数学问题中蕴含的数学本质;三是能整体把握解题方向，且能对答题思维进行自我监控，及时纠错;四是能跳出数学问题本身，培养学习者全面而深入的思维习惯.[4]这四个思维层面实际上与前者相当吻合，或者可以说前者的四个层面包含于全景思维之内，这时全景思维就显现出其优势.

二、全景思维的作用及其运用步骤

全景思维主要应用于数学解题当中.由于数学知识的难度按层级结构递增，各层知识点间相互贯通，巧妙联系，且各层间紧密联结.因此，学生在解决数学问题前，需要对已学知识有全景性的把控，当其心中有“会当凌绝顶，一览众山小”的底气，才能全面细致地看待数学问题，从而迎刃而解.全景思维以大空间、系统性的思考模式去打开学生封闭的思维常态，恢复学生的个性思维和创造思维.在解决数学问题的过程中，该思维首先指导我们以全景的方式洞察和联想知识点与知识点之间的相关联系，巧妙运用多种化归方法.当我们遇到难题时，先有针对性地思考“这道题难在哪？”“为何化难为易？”进而想方设法把未解决或难以解决的问题转化为已解决或容易解决的问题.在解题过程中，全景思维发挥其自我监控性，督促我们及时检验，以免“一步错，步步错”.在解题过后，我们应总结每一道题或某一类题所用知识点，解题策略及出错的原因.对自己答题策略进行反思，与他人答题策略进行对比，进而修正、丰富自己的思路和方法，使自身全景思维得到加强.[4]以上是全景思维大致的应用步骤，下面本文将从这四个方面分别阐述全景思维在解决数学问题中的应用.

（一）全景建立数学知识结构体系

首先，它可以帮助学生持续激活已掌握的知识，形成良好的知识结构网络，使学生有完备的依据对问题做出准确而全面的指導性判断.而且，它使学生在以后的学习中更有逻辑地进行思考和判断，提高数学关联能力和抽象概括能力.[5]俗话说，“磨刀不误砍柴工”，要解决数学问题首先要深刻理解数学理论基础，明确每个定义和定理的内涵与外延，有清晰全面的数学知识网络体系做武器才能去解题.

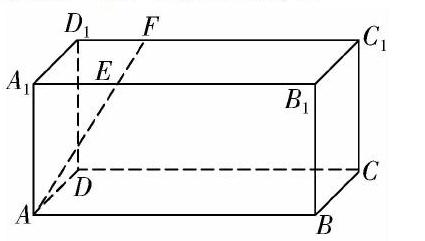
例如，（2015年高考全国2理科卷第19题）如图所示，长方体ABCD-A1B1C1D1中，AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F=4.过点E，F的平面α与长方体的面相交，交线围成一个正方形.在图中画出这个正方形;求直线AF与平面α所成角的正弦值.

该题难度较小，但需要学生对正方形、勾股定理、线面角等定义有清楚的认识，且积累下一定的作图能力、空间想象能力与解决实际问题能力等数学素养做支撑，才能快速无误地解答此题.

（二）精准全面地分析和把控题意

全景思维能帮助解题者遇到数学问题时，全面收集信息，挖掘出题目隐含条件，透过问题看到其所反映的数学本质.它首先引领解题者抓住问题中图形的几何特征、文字所表述的数量关系、数学符号的形式化暗示，透过形式化语言分析出其所蕴含的结构特征和运算法则;然后指导解题者确定问题转化方向，解题方向有可能是不定且多维的，要视题目具体情况而定.在明确解题方向之后，解题者展开联想，运用全景思维从知识结构体系中抽取所可能用到的知识，进而找出题目所给的条件与问题的联系.而从条件所涉及的知识点到所要求的问题点，中途可能要遍历多个关联点，这些关联点连接起来就是解题的推理链，即该题的解题思路.

例如，上述第二小题是求线面角的正弦值，这种题目有两个大方向的解法：向量法和几何法.几何法中首先要找出AF在面EFGH中的映射（记为AO），即证明AO⊥面EFGH.由观察图形的几何特征和边长的数量关系，不难猜想O在EG上，进而需要证得AO分别垂直于GH和EG，由题目所给的条件显然问题得解.

（三）拓展思路的广度和深度

实际上解决一个问题可行的推理链可能是多样的，就如实际生活中你从出发地到目的地可采取多种多样的出行方案.然而，我们通常希望找出那条换乘次数最少，花费最少而且耗时最少的路线.同理，解题也需要在多种解题思路中找最简便直接的途径，而当发现思路纷杂或计算量太大时，则会才用特殊化法、数形结合法、反推法等方法以退为进来求解问题，又或者先抓住问题隐藏的一般规律，再用该规律反解问题.探索出一般规律的新意义，创新典型题的解题方法，学会一题巧解和多解.比如，上述题目如果一时找不到映射AO，也可以采用模糊化的方法：等体积法来求解.设AO为锥A-EFG的高，利用V锥A-EFG=V锥F-AEG求得AO的高，也可以解出此题.此外，理科生还掌握着一条解空间几何的救命稻草：建立适当的空间直角坐标系用纯向量的方法也一样使问题得解.可见，全景思维能为我们拓展多种思路.

本题考查对函数、不等式的综合应用，要正面难度较大.通过观察四个选项的特征不难发现，可用排除法求解.当a=0时，f（x）的解集有无数个整数解，故排除A和B.而C和D选项排除关键在于a能否等于34.当a=34时，f（x）=ex（2x-1）-34（x-1）<0，设g（x）=ex，h（x）=34（x-1）（2x-1），结合g（x）和h（x）的图像可得f（x）<0的解集中有唯一的整数解x=0，故a=34适合题意，选D，题目得以巧解.

（四）答题思维缜密且能够自我监控

全景思维强的学生在解题时目标明确，解答过程瞻前顾后，及时检测自己所选的解题策略的效果，对自己所导致的失误进行反思和把控，能纠正错误的思维定式.这属于全景思维的元认知层面.可见，全景思维可帮助学生按题目要求答题，清楚地表述答题步骤，得出合理的计算结果.例如，解决函数问题应先考虑定义域，换元时应注意所换字母范围的变化，使用基本不等式时应留心等号成立的条件等等，还包括解题过程的逻辑性和规范性，将计算结果用不同的方法进行演算，这些都需要很好的全景思维来调控.

当然，全景思维也存在其应用的局限性，它依赖于学习者的经验背景和学习自主性，若学习者自身的知识储备量较少，是很难发挥全景思维的作用.而学生日常的学习过程中如果没有自觉积累知识和解题策略，不愿意尝试一题多解，其全景思维也难以很好地应用在解题当中.

三、全景思维的应用案例

四、結 语

数学知识本身具有全景性，我国越来越注重多元与开放的数学解题教学，且越来越重视数学思想方法运用和变式教学的理论探讨.[6]良好的全景思维在数学解题时屡试不爽，我们没有一种方法能解答所有数学问题，但全景思维给了我们一种解题的通用思维能力.只有经常对所学知识进行多方向贯通联结，对数学问题多维度思考，及时总结反思;在新的问题情境下灵活运用有效的思维策略，才能在解题过程中收获“山重水复疑无路，柳暗花明又一村”的惊喜.

【参考文献】

[1]刘京莉，李佳.国内外数学问题解决研究热点与趋势探析[J].教育导刊，2018（5）：58-62.

[2]乔治·波利亚.数学的发现——对解题的理解、研究的讲授·第2卷[M].呼和浩特：内蒙古人民出版社，1981.

[3]罗增儒.数学解题学引论[M].西安：陕西师范大学出版社，2016：38-40.

[4]张宏伟.我与“全景式数学教育”[J].中国教师，2017（10）：47-51.

[5]邵玉丽.统筹知识“网”“点”提高学生素质[J].商丘职业技术学院学报，2004（4）：87-88.

[6]方均斌.“数学问题解决”研究的中国特色[J].课程·教材·教法，2015（3）：58-62.