整数上离散高斯取样的常数时间实现方法
卢嘉嘉,杜育松
(中山大学 数据科学与计算机学院,广州 510006)
0 概述
格密码被认为是未来能够抵抗量子计算机攻击的一类新型密码[1-2]。研究表明,使用量子计算机有可能破解基于大整数分解或离散对数问题的传统公钥密码,如RSA和椭圆曲线公钥密码。常见的数字签名和公钥加密等密码学原语,都已经有了基于格密码的实例[3-4]。
离散高斯取样是指在n维格中取出格点,满足特定参数的n维离散高斯分布[5]。离散高斯取样在格密码中具有基础性作用,是许多格密码体制实现的基本操作[6-7]和决定这些密码体制安全性的重要因素[8]。整数上的离散高斯取样是一般离散高斯取样的子问题,也是实现一般离散高斯取样的核心子过程[5,9],主要指产生符合含特定参数的一维离散高斯分布的整数[10]。由于整数上的离散高斯取样相比于一般离散高斯取样,具有计算简单且取样效率高的特点,因此在一些密码体制中直接作为一般n维格上的离散高斯取样被使用[11]。然而,传统的连续高斯分布取样算法不能直接应用于这种离散的情形[12],现有的整数上的离散高斯取样算法预计算存储量大,无法抵御计时攻击,或者取样性能不高,无法很好地满足格密码实现的要求[13],一定程度上制约了格密码方案的推广与应用。因此,研究整数上的离散高斯取样算法对于格密码的实现具有重要的理论和实际意义。
针对密码方案的侧信道攻击是密码学领域非常重要的研究课题。但格密码体制有可能因为针对离散高斯取样过程的计时攻击导致秘密信息泄露[14-15],而先前设计的整数上的离散高斯取样算法大多无法抵御计时攻击。因此,在保证离散高斯取样功能和效率的同时,如何防止离散高斯取样由于计时攻击造成的秘密信息泄露成为一个倍受关注的问题[16]。
基于Knuth-Yao算法的离散高斯取样算法的优点是取样速度快,不需要在线的浮点运算,并且能够实现常数时间取样。例如,文献[17-18]将基于Knuth-Yao算法的取样算法转化为常数时间的对随机比特串的位操作,既保证了取样速度,又防止了由于计时攻击造成的秘密信息泄露。然而,在实现该算法的过程中,将取样过程转化为对随机比特串的位操作包含了复杂的预计算过程(需要编写专门的复杂预计算程序去实现,预计算中涉及的部分参数还需要通过额外的实验数据比对才能确定),并且实现位操作的代码规模巨大,有可能导致硬件实现中所需的电路规模较大,不适合在存储资源受限的电子设备上实现。
针对整数上离散高斯取样的问题,本文提出一种常数运行时间的简单实现方法。该方法在支持单指令多数据(SIMD)的设备上采取向量化操作手段,从而提高取样速度。
1 预备知识
1.1 离散高斯分布及取样




1.2 Knuth-Yao算法

实际上在采样操作之前不需要将DDG树按树的形式存储,它可以从概率矩阵中被快速地构造并使用。考虑样本点概率的二进制扩展,它们可以写为二进制矩阵的形式,写成的矩阵被称为概率矩阵并由M表示。对于i,j≥0,设pj=pj0+pj12-1+pj22-2+…+pji2-i+…是第j个样本点概率的二进制展开,其中pji∈{0,1}。在概率矩阵M中,第j行Mj即为(pj0,pj1,…,pji,…),对应第j个样本点概率的二进制展开。概率矩阵与DDG树的对应关系如图1所示。

图1 概率矩阵与对应的DDG树Fig.1 Probability matrix and corresponding DDG tree
基于对DDG树内部节点相对距离的分析,文献[12]将基于Knuth-Yao采样过程描述为如算法1所示的形式。
算法1基于离散高斯分布的Knuth-Yao取样算法[4]
输入λ+1行的概率矩阵M
输出采样结果x
1.j←0,d←0
2.采样均匀随机比特r
3.d←2d+r
4.for i←λ down to 0 do
5.d←d-M[i][j]
6.return i if d=-1,否则continue
7.end for
8.j←j+1并返回步骤2
在算法1中,d表示DDG树访问节点和同层最右节点的距离,j表示矩阵列索引,r取1表示往靠近内部节点的方向游走。
对于一个具有无限支撑的离散分布,样本点的数量及其概率的二元展开式可能是无限的,这将导致生成一个无限规模的概率矩阵。在现实中必须对概率矩阵进行截断处理,同时保证足够的精度。如算法1中概率矩阵M的行数被设置为λ+1,使得算法输出绝对值大于λ/2的概率是可忽略的。同时,矩阵M的列数也是有限的,因为每个样本点的概率值只能以有限的精度存储。一般来说,对于给定的σ,取λ=12σ(表示算法输出的整数在-6σ~6σ之间),而矩阵的列数可以被设置为64 bit,从而保证大多数应用的精度需求[10,19]。
1.3 穷尽比特扫描的Knuth-Yao算法
为抵御计时攻击,可以将标准的Knuth-Yao取样算法改造成为常数运行时间的“穷尽比特扫描”的Knuth-Yao取样算法。具体地,要求执行算法在得到d=-1时,并不立即返回输出值,而是设法记录输出值,并继续完成对整个概率矩阵的遍历。
2 常数运行时间的实现方法
为减少运行时间,本文考虑对算法1进行改进。主要思想可以分为3点:快速初始化变量d;快速确定d=-1时所在的概率矩阵列,即d=-1时变量j的值;按比特扫描概率矩阵的第j列,返回输出值。为实现上述方法,在预计算阶段,需要确定并记录概率矩阵各列的汉明重量(记为wt),从而借助概率矩阵各列的wt实现d的快速初始化和更新。例如,参数σ取6,则概率矩阵大小为73行64列。一列的wt较大概率不会超过64,因此各列的wt可以用6位二进制数来表示。
2.1 快速初始化变量
在算法1中,变量d被初始化为0,以d←2d+r的方式进行更新,然后按比特扫描概率矩阵,并在每扫描完一列时再以d←2d+r的方式进行更新。
注意到一个给定概率矩阵的前若干列有可能均为零列,即wt=0。例如,当参数σ=6且c=0时,概率矩阵的前4列均为零列。一般地,如果概率矩阵的前N列均为零列,那么对于j=0,1,…,N-1,算法1的第4步~第7步对变量d没有影响。或者说,在扫描概率矩阵的前N列时,变量d仅以d←2d+r的方式进行更新,且一定有d≥0。设执行算法时产生随机比特串为b0b1…bN-1…。可以验证,在即将扫描概率矩阵的第N列时,变量d的值满足:
d=b0×2N-1+b1×2N-2+…+bN-1×20
即变量d的值为:将比特串b0b1b2…bN-1看成是二进制数时所表示的十进制整数。于是,在概率矩阵的前N列均为零列时,可以直接将变量d初始化为(b0b1…bN-1)2,并令j=N,避免遍历零列造成不必要的时间开销。
2.2 d=-1时所在列的快速确定
算法1通过对概率矩阵的列逐比特遍历以更新d的值。如果记录了的概率矩阵每一列的wt值,从首列非零列开始,逐列检查d-wt是否小于等于-1,当首次发现d-wt≤-1时,就可以确定对应的列即为输出结果所在的列。相反,如果d-wt>-1,则令d←d-wt,再以d←2d+r的方式更新变量d的值,然后对概率矩阵下一列继续检查d-wt,直到在某一列时,发现d-wt≤-1。
称输出结果所在的列为目标列,在确定目标列的过程中,若找到满足条件的列随即停止扫描,攻击者将有可能检测到程序停止运行,通过计时攻击的手段确定目标列所在范围,而目标列的信息泄露进而将导致输出结果的信息泄露。为了防止这一问题,需在确定目标列时,不立即停止检查d-wt,而是设法记录目标列,继续完成对剩余所有列的检查,从而保证常数的运行时间。对上述确定目标列的方法在下文以C/C++伪代码的形式进行描述。
1.WhichCol←FirstNonZeroCol,s←1
2.for j←FirstNonZeroCol to 63 do
3.d←d+s (d+(rnd64bits&1))
4.rnd64bits←rnd64bits≫1
5.s←s&unsigned(d>=ColWts[j])
6.d←d-s ColWts[j]
7.WhichCol←WhichCol+s
8.end for
在伪代码中,rnd64bits为预先生成的64位随机比特串。FirstNonZeroCol表示概率矩阵的首列非零列。数组ColWts存储概率矩阵各列的wt。引入变量s作为指标,并用WhichCol表示目标列的位置。在确定目标列的过程中,j从概率矩阵的首列非零列FirstNonZeroCol开始,直到j=63,检查完概率矩阵后续所有列。
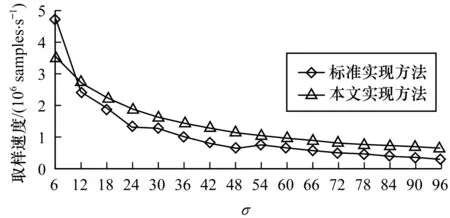
当首次出现d 在确定目标列WhichCol和对应的d值后,按比特扫描概率矩阵的第WhichCol列确定d=-1时所在的行WhichRow,即可确定返回的输出值。为了确保常数运行时间,同样引入变量s作为指标。初始化s为1,在确定WhichRow后,s由1置为0,程序保持对第WhichCol列所有剩余比特的扫描。变量WhichCol虽然继续参与运算,但它的值不再变化。 需要指出的是,为了抵御可能的cache攻击[14],概率矩阵应按行来存储,而不应按列来存储。例如,参数σ取6时,概率矩阵有73行64列,这时应使用73个uint64_t型整数,而非64个bitset<73>("…")型对象来存储整个概率矩阵。如果按列来存储,因为程序会只读取其中一个bitset<73>型对象,cache攻击有可能确定当前正在扫描的概率矩阵的第WhichCol列,从而造成输出值的信息泄露。当概率矩阵按行来存储时,扫描概率矩阵的第WhichCol列需要概率矩阵所有行的数据参与计算,从而避免了cache攻击的可能。 在处理器i7-8550U内存为16 GB的笔记本电脑上,使用g++编译器进行编译,实现了本文设计提出的取样过程,涉及的均匀随机数通过AES-256-CTR方式产生。图2比较了标准实现方法和本文实现方法的取样速度。 图2 参数σ控制下的算法采样速度对比Fig.2 Comparison of algorithm sampling speed under parameter σ control 从图2可以看出,本文的常数运行时间实现方法较算法1的标准实现方法速度略快,可以满足密码方案的性能需求。对于“穷尽比特扫描”版本的取样算法,当σ=6时,其取样速度仅为0.155 5×106samples/s,并且随着σ的增大,取样速度将低至无法使用。 此外需要说明的是,图2涉及的算法1的两种实现方法在初始化变量d时,均使用了2.1节中的快速初始化方法,以避免遍历零列造成的不必要的时间开销。 本文算法中的概率矩阵行数被设置为12σ+1,实际上,对于中心化离散高斯分布,由于概率分布的对称性,概率矩阵只需6σ+1行,这使得可以进一步提高取样算法的实现效率。本文为了保证普适性,考虑实现的是非中心化离散高斯分布的取样。 在所有具有常数运行时间的、中心化离散高斯分布的取样算法中,到目前为止,文献[17]设计实现的取样算法是速度最快的算法,达到15×106samples/s。本文算法的取样速度虽然未能达到文献[17]算法的速度,但是优势在于预计算过程简单,存储量小,对于资源受限的设备更加友好。 具体来说,本文的预计算过程仅是计算给定离散高斯分布的概率矩阵,并确定概率矩阵每个列向量的汉明重量。预计算存储则只包括概率矩阵和每个列向量汉明重量的值。例如,对于参数为σ=6的中心化离散高斯分布,概率矩阵规模可以设置为73行64列,可以保证多数应用所需的安全精度。73个行向量用73个uint64_t型整数存储,而每个列向量汉明重量的值则可以用64个uint8_t型整数存储,再用一个uint8_t型整数记录一个非零列向量的位置,因此总的存储量为73×8+64+1=649 Byte。如果需要更大的安全精度,则可以增加概率矩阵规模,如将概率矩阵的行和列数量都加倍,总的存储量不超过4×649≈2.5 KB。 文献[17]算法实现之前需要先将基于Knuth-Yao的取样算法转化为对随机比特串的位操作(布尔表达式)。这一过程需要编写复杂的预计算程序去实现,涉及Karnaugh图优化技术或者Espresso启发式逻辑最小化工具,并且预计算中涉及的部分参数需要通过额外的实验数据比对才能确定。当离散高斯分布的参数σ发生变化时,上述的整个转化过程还需要重新进行。因此,其整体预计算开销较大。该算法在实现时,需要在源代码中写入大约18×103个位与运算 AND、5×103个位或运算 OR以及11×103个位非运输 NOT[17]。如果每个运算占用一个字节,那么源代码规模将至少达到18+5+11=34 KB,远大于本文的2.5 KB。 目前的CPU多数支持单指令多数据(SIMD),可以并行处理包含多个数据的向量。本文提出的取样算法也可以通过使用SIMD将其进行向量化,从而实现取样速度的进一步提高。特别地,可以使用Agner Fog的VCL (C++向量类库)对取样算法进行向量化[20]。VCL向量化类库在SIMD的支持下为整数和浮点数提供了优化的向量操作,使程序员更容易编写向量化代码,而不必为调用SIMD指令而使用汇编语言或内部函数。 VCL类库支持Vec64c数据类型。如果AVX512指令集在目标CPU上是可以使用的,那么Vec64c是具有64个int8_t型整数的向量类型。然而,目前大多数CPU支持AVX和AVX2指令集,但不支持AVX512。因此,本文仅使用了Vec32c类,它在AVX2的支持下并行处理具有32个int8_t型整数的向量。结合VCL类库,可以将实现过程分为PopulatePoolColumns()和Sampler()两个子函数。PopulatePoolColumns()函数每次产生两个Vec32c类型的向量vWhichCol和 vd,其中vWhichCol对应概率矩阵中的目标列,算法最终输出的32个整数将分别通过扫描这些目标列来产生。Sampler()子函数则依次完成这些扫描任务,且每次扫描时的d值分别对应于vd中的分量。在相同实现环境下的实验结果表明,当σ=6时,使用上述向量化实现方法可以使得取样速度提升至14.9×106samples/s。 本文给出一个整数上离散高斯取样的常数时间实现方法。通过使用单指令多数据将其进行向量化操作,并在单指令多数据的处理器上使用向量化技术,以获得更好的取样速度。该方法预计算过程简单,存储量较小,对于存储资源受限的电子设备更加友好。本文的实现方法预计算过程简单,下一步将研究中心可变的(非中心化)离散高斯分布常数运行时间的取样算法,以尽可能减少预计算存储量。2.3 按比特扫描概率矩阵的第WhichCol列
3 本文方法的实现与比较
4 算法的向量化实现
5 结束语

