线段求值不简单 勾股定理来引路

文 顾晶晶

勾股定理即直角三角形的两条直角边的平方和等于斜边的平方。众所周知，其不仅历史悠久，而且应用广泛。在求线段的长时，将勾股定理与一些基本图形或一些基本数学思想如方程思想、数形结合、建模思想等相结合，能为线段求值“引路”助力，可谓简约而不简单。

一、构造基本图形

例1如图1，正方形ABCD的4个顶点在相互平行的四条直线l1、l2、l3、l4上，且l1与l2，l3与l4之间的距离分别为1，l2与l3之间的距离为2，求AD的长。

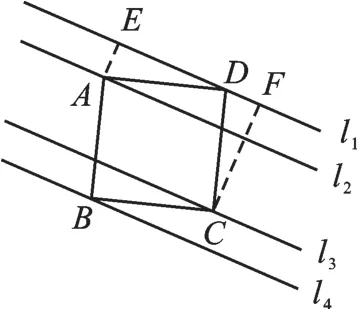
图1

【解析】因为已知l1与l2之间的距离为1，所以我们可以赋予AD一个适当的求值“环境”：过A作AE⊥l1，垂足为E，则AD是Rt△ADE的一条边。已知AE=1，则由勾股定理可知，求出DE的长即可解决问题。

我们回看已知条件，不难发现，l1与l3之间的距离为3。结合正方形的性质，过点C作CF⊥l1，垂足为F。由全等三角形的基本图形“K”字形，我们可以证得△ADE≌△DCF（AAS），则DE=CF=3。

所以，在Rt△ADE中。

二、结合方程思想

例2如图2，折叠矩形的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，求EC的长。

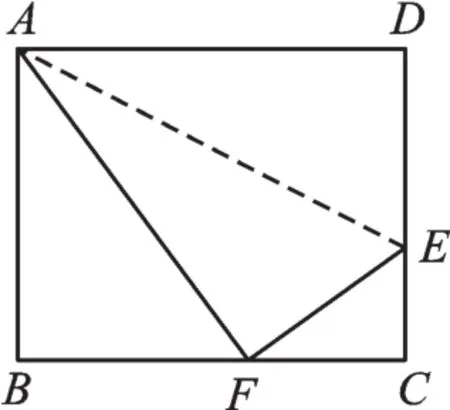
图2

【解析】由矩形可得直角，所以EC可放在Rt△CEF中解决，那么，由勾股定理可知，我们需要求出EF、CF的值。

由折叠可知：AF=AD=10，DE=EF。在Rt△ABF中所以CF=4。如何求EF的长？我们发现，EF与EC存在数量关系：EF+EC=ED+EC=CD=8，所以，勾股定理为“引路人”，方程为“铺路石”。设CE=x，则EF=8-x，由勾股定理得方程：x2+42=（8-x）2，不难求得x=3，即CE=3cm。

三、数形结合

例3求代数式的最小值。

【解析】我们观察式子，发现其形如勾股定理中，已知两条直角边a、b，求斜边c的公式，即c要求的代数式的前半部分可以看作直角边分别是x和5的直角三角形的斜边，后半部分可以看作直角边分别是6-x和3的直角三角形的斜边。

我们发现，x的值是变化的，6-x的值也在变化，但动中有定，两者的和是个定值6。因此，数形结合思想油然而生。我们把“式”变成“形”，构造Rt△ABC和Rt△DEF，使直角边BC和EF在同一直线上，且点B、E重合（如图3所示）。

图3

则 有CF=BC+EF=x+（6-x）=6，AC=5，DF=3，问题转化成：点B在线段CF的何处时，AB+DB最短？

根据“两点之间线段最短”，连接AD，则线段AD就是AB+DB的最小值。那如何求AD呢？

我们赋予AD一个有直角三角形的求值“环境”：作AG⊥DF交DF的延长线于G。所以，在Rt△ADG中，由勾股定理可得，AD所以，原代数式的最小值为10。

同学们，勾股定理为线段求值创造了一个良好的求值平台，我们在以后解题过程中还要继续多思考，多应用，多探究，慢慢体悟其中的奥秘。