基于改进多点估计与最大熵的概率谐波潮流算法

王庆岩，孙媛媛，谢香敏，李亚辉，许庆燊，张 岩

（1. 山东大学电网智能化调度与控制教育部重点实验室,山东省济南市250061；2. 国网山东省电力公司电力科学研究院,山东省济南市250003）

0 引言

当代电力系统中,电力电子装置广泛应用于电能的发、输、配、用各环节,由此引发的谐波污染愈加严重。谐波潮流计算可有效计算系统中各节点的谐波畸变水平［1-2］,是谐波治理的基础。传统的谐波潮流未考虑随机因素,只反映系统某一时间断面的状态,而当今电力系统中不确定性增强［3-4］,谐波潮流也呈现出随机性、波动性等特征,研究不确定性谐波潮流具有重要意义。

不确定性谐波潮流的概率分析方法可分为模拟法、解析法与近似法［5］。模拟法以蒙特卡洛仿真（Monte Carlo simulation,MCS）法为代表,基于大量采样,计算准确但效率低［6］。解析法以卷积法和半不变量法为主,卷积法不易实现,半不变量法中谐波潮流方程的线性化较复杂,且当输入变量波动较大时,基准点的线性化会引入误差［7］。近似法以点估计法（point estimate method,PEM）为主［8］,通过少量确定性的计算获得输出变量的统计特征,无须对潮流方程进行线性化,计算简单且较为准确,因此在不确定谐波潮流分析中获得应用。其中,文献［9］从谐波节点电压方程入手,分析了风机接入后的谐波水平；多变换器系统中的不确定性谐波也基于点估计法得以计算［10］。然而,无论是2m还是2m+1 点估计,都属传统点估计,受限于采样点数量,估计精度受随机变量个数及分布的影响。另外,上述方法一般结合级数展开来实现随机变量的概率密度函数拟合,但级数展开存在截断误差,不易拟合概率密度函数尾部特征,易在部分区域出现概率密度为负的情况［11］。

传统点估计方法性能提升可通过构造多重采样点实现,因此有文献研究了多采样点估计在基波概率潮流中的应用［12］。由于概率谐波潮流存在不同的分析场景,相比基波潮流存在频谱不确定以及谐波电流幅值相角双重不确定性等问题,分析过程的不确定性以及非线性程度进一步增强,因此不同分析场景下,概率谐波潮流统计特征的准确求解与概率密度函数的有效拟合仍有待研究。文献［13］提出基于随机变量联合分布的Rosenblatt 变换,实现原变量空间与标准正态变量空间的转换,从而简化采样点与权重的计算,进而实现谐波分析,但现实中随机变量多以样本形式给出,联合分布不易获取,且仅对谐波潮流的单一分析场景进行研究,同时对多点估计后期的概率密度函数拟合关注较少。

为实现不同分析场景下概率谐波潮流中统计特征以及概率密度函数拟合精确度的提升,提出一种改进多点估计与最大熵（improved multi-point estimate method and maximum entropy,IMPEM&ME）的概率谐波潮流算法。基于随机变量的离散近似理论,确定独立标准正态分布随机变量的多重采样点和权重；根据随机变量空间变换,获得功率、谐波电流等任意分布随机变量的权重与采样点,计算谐波电压等输出随机变量的统计特征,进而基于最大熵分布求取输出随机变量的概率分布。所提方法通过采样点数的增加,有效提升了待求变量统计特征的计算精确度；基于随机变量空间变换避免了原变量空间获取多点时的复杂计算,并可有效处理变量之间的相关性；结合最大熵概率分布,可较好地保证所求概率分布拟合的准确度。

1 改进多点估计和最大熵概率分布

1.1 基于随机变量离散近似的多点估计

点估计法可应用于概率谐波潮流计算。三点估计通过匹配输入变量的前四阶矩,求得采样点与对应权重［8］,从而计算待求变量的原点矩或中心矩,然而少量的采样点使得计算精度受限。基于高斯数值积分的离散近似可获取多个估计点与权重［14］,实现原点矩的准确求解。若通过离散近似随机变量x的分布,则应满足：

式中：E（·）为期望函数；n为采样点数量（多点估计下,n＞3）；l为 阶 数；xk与pk分 别 为 第k个 采 样 点 与权重。

通过对应的采样点与权重实现随机变量原点矩的匹配,从而逼近原连续分布。此时,对于单输入随机变量x的函数y(x),其l阶原点矩亦可通过上述采样点与权重获取,即

对于随机变量x,假设取n个采样点,则式（1）中共有2n个未知数,需2n个方程才可定解,可通过匹配随机变量的前2n-1 阶原点矩并结合各权重之和为定值来实现。式（1）可展开为：

通过式（3）求解实现离散近似所必需的随机变量的采样值与权重,获得待求输出变量的统计特征。

当输出变量y的自变量中包含m个随机变量时,应对每一个随机变量进行上述运算,求解每个输入随机变量的采样点与权重,并将式（3）中对应随机变量期望值的权重p1进行如下替换,以保证输出变量含多个输入随机变量时估计的准确性：

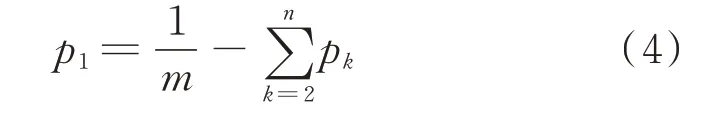
将多输入随机变量下第i个随机变量的第k个采样点记为xi,k,对应权重记为pi,k,此时对于含有m个自变量的输出变量y,可通过单变量确定性评估方法获取待求变量的原点矩,如下式所示：

式中：μ表示随机变量的期望,下标表示对应的随机变量。

1.2 多点估计法改进

当输入的随机变量为任意分布时,高阶原点矩不易获取,直接计算采样点过程复杂。考虑到标准正态分布变量u采样计算简单,因其l阶原点矩可通过递推公式获得,即

为保证计算效率,同时便于处理输入随机变量之间的相关性,应用Nataf 变换理论对基于离散近似理论的多点估计进行改进,使得采样值与权重的计算在标准正态分布变量空间内进行,并通过Nataf反变换实现任意分布随机变量空间下采样点与权重的求解,以满足实际需要。

当任意分布的随机变量之间相互独立时,应用Nataf 变换理论。对任意分布的随机变量xi,其采样点xi,k与对应的标准正态分布空间内的采样点ui,k之间应满足：

式中：F（·）和Φ（·）分别表示原任意分布和标准正态分布随机变量的累积分布函数。

若原任意分布随机变量组成的向量中某些随机变量具有相关性,记其相关系数矩阵为ρ。Nataf 变换后,所得的各标准正态分布随机变量组成的向量U依然具有相关性［15］,相关系数矩阵为ρ1。该矩阵一般对称正定,进行平方根分解可得下三角矩阵L。由Z=L-1U可实现相关性的消除,此时Z向量内各随机变量服从独立标准正态分布。基于独立标准正态分布空间计算采样点与权重,并结合矩阵变换及Nataf 逆变换可实现具有相关性的任意分布随机变量采样点与权重的求解。

1.3 改进多点估计框架下的最大熵概率分布

信息熵用以表征信息的不确定性,最大熵原则认为在满足原点矩约束条件下,信息熵最大的概率分布是最客观的。在改进多点估计框架下,最大熵可表述为：

式中：w（y）表示随机变量y的概率密度函数；C为应满足的原点矩约束的阶数。

引入拉格朗日乘数法求解上述问题,可得到解析解：

式中：λc为对应于c阶原点矩的拉格朗日乘子（c取0时,原点矩为1）。通过牛顿-拉夫逊法求得未知参数λc,获得最符合客观实际的概率分布［16］。

相比于传统通过有限项的级数展开拟合概率密度函数的方法,最大熵概率拟合利用有限的信息,对未知信息作最少的假定,所获得的概率分布是基于有限信息获得的最客观的分布,同时基于负指数形式,保证了所求解的概率密度函数值不小于0。

2 概率谐波潮流实现框架

2.1 确定性谐波潮流计算

谐波潮流计算方法可分为统一迭代法、交替迭代法、解耦法以及非迭代式方法。解耦法将基波计算与谐波计算解耦处理,计算过程得到简化,同时也保证了精度,在谐波潮流计算中获得广泛应用。解耦法谐波潮流首先计算基波潮流,考虑到谐波电气量相比基波电气量一般较小,因此在求解基波潮流时可忽略谐波影响。含分布式电源（distributed generator,DG）系统的基波潮流计算,DG 接入节点可依据其容量以及并网控制方式等确定节点类型［17］。

当获取基波状态后,需根据不同的谐波源特性［18］计算谐波电流。负荷侧的非线性负荷可采用恒流源模型、诺顿模型、谐波耦合导纳矩阵模型或非线性建模方式［13］确定其谐波电流与负荷参数的关系；对于发电侧可再生能源DG 并网,可基于数据拟合［19］或输出阻抗模型［20］等建立输出的谐波电流与可再生能源DG 出力或运行状态之间的联系。依据谐波源特性可通过迭代或非迭代的方式确定谐波源所注入的谐波电流。上述非线性负荷与可再生能源DG 的谐波电流可分别表述为：

式中：I˙h表示谐波源的h次谐波电流相量；Fh表示谐波源特性方程；下标l 与g 分别表示负荷和可再生能源DG；对非线性负荷,V˙与V˙2和V˙3等分别表示基波与对应次数的谐波电压相量,下标为谐波次数；Cl表示负荷参数；对可再生能源DG,Ci与Cw分别表示内部运行或控制参数以及外部参数。

当系统中的主要谐波源有谐波电流监测装置时,可直接依据监测所得的谐波电流以及网络参数计算系统各节点的谐波电压。考虑到谐波节点电压方程的求解为相量运算,可通过实部虚部解耦实现谐波电压相量的求解：

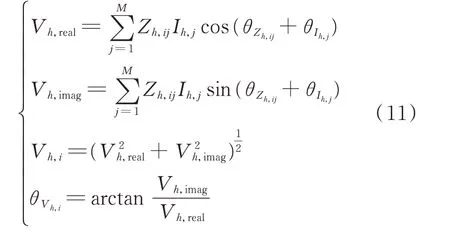
式中：Vh,real和Vh,imag分别为节点i的h次谐波电压实部分量和虚部分量；M为系统独立节点数；Zh,ij和θZh,ij分别为谐波节点导纳矩阵逆矩阵Zh中第i行第j列元素的幅值和相角；Ih,j和θIh,j分别为节点j发出的h次谐波电流的幅值和相角；Vh,i和θVh,i分别为节点i的h次谐波电压的幅值和相角。

2.2 IMPEM&ME 框架下的概率谐波潮流

概率谐波潮流分析中,首先应对节点功率或谐波源注入电流等输入量建立概率模型。与功率以及出力相关的随机变量,负荷采用正态分布,风速采用Weibull 分布,光强采用Beta 分布；谐波电流幅值与相角可通过正态分布及均匀分布进行描述［21］。

对于不确定性谐波潮流,无论是基于解耦法或是基于谐波源监测数据的直接求解,不同分析场景下谐波潮流方程中输入的随机变量与输出的谐波电压相量之间均存在一定的映射关系。基于解耦法时,输入随机变量为不确定性负荷、风速、光伏等,考虑可再生能源出力与外部天气状况的关系以及谐波电流含有率与DG 出力的关系,即可建立输入与输出之间的映射关系,如式（12）所示；基于谐波源监测的谐波电流数据直接求解时,考虑谐波电流幅值与相角的双重不确定性,输入变量为不确定性谐波电流幅值及相角,此时输入与输出之间的映射关系可表述为式（13）。

式中：H（·）与G（·）分别表示基于解耦法与基于谐波电流监测数据时,h次不确定谐波电压向量矩阵V͂h与输入变量的映射关系；L͂、W͂和S͂分别为系统中输入的不确定性负荷、风速和光强矩阵；I͂h和θ͂h分别为不确定性h次谐波电流的幅值和相角矩阵。

考虑到谐波潮流不同分析场景下映射关系以及输入随机变量的概率分布,可通过IMPEM&ME 方法获得谐波电压等输出随机变量的统计特征与概率密度函数,具体求解过程如图1 所示。

图1 基于IMPEM&ME 方法的概率谐波潮流计算流程Fig.1 Flow chart of probabilistic harmonic power flow calculation based on IMPEM&ME method

1）基于解耦法或谐波源监测数据,根据基波潮流方程及式（10）、式（11）建立确定性谐波潮流方程,确定系统输入变量与输出变量及其对应的映射关系。

2）基于经验分布或实际数据,建立输入随机变量的概率描述,确定输入变量的累积分布以及各输入随机变量之间的相关系数矩阵。

3）基于式（3）、式（4）、式（6）,确定独立标准正态分布变量的多重采样值以及权重,并基于相关系数矩阵,依据矩阵变换与式（7）实现原任意分布变量空间内采样点的求取。

4）依据每一随机变量所取的采样点,按式（5）的形式对输出的随机变量进行确定性评估。当某一随机变量取采样值时,其他随机变量取期望,进行若干次确定性计算,通过加权的形式获取输出变量统计特征。建立约束条件,基于式（8）求解最大熵概率分布,实现概率密度函数的重构。

3 算例分析

3.1 基于解耦法的概率谐波潮流

以改进的IEEE 33 节点系统为例［22］,研究改进多点估计（以5 个采样点为例）与最大熵结合法在解耦谐波潮流分析场景中的性能。光伏与风机分别接入节点16 与33,采取文献［20］中的DG 典型特性,将风机节点、光伏节点简化为PQ节点,且认为光伏系统只输出有功功率,风机系统发出有功功率,吸收无功功率,且均经过并网装置接入电网。不计负荷注入系统的谐波电流与系统背景谐波,谐波节点导纳矩阵根据不确定因素取期望值时系统基波参数以及对应谐波次数获取。DG 经变换器接入节点为谐波源节点,考虑可再生能源DG 节点注入的谐波电流与其出力有关,因此以文献［19］给出的分段线性关系确定5 次谐波电流含有率与DG 出力之间的关系,谐波电流相角频谱相对基波电流相角频谱超前π/12。

负荷节点的期望与原系统相同,功率因数在负荷与出力波动期间认为保持恒定,并取变异系数为5%。风机的切入风速、额定风速与切出风速分别为3,14,25 m/s,所研究时段内该地区的风速、光强的分布参数（如均值μ与变异系数）以及风机的有功出力的额定功率Pr、光强为1 kW/m2时光伏输出的功率Pmax和对应的功率因数角δ等参数见附录A 表A1。风速Weibull 分布与光强Beta 分布的参数可依据所研究时段风速、光强的期望与变异系数求取,风机、光伏的出力与风速、光强的关系可分别依据文献［23-24］获得。

不计输入变量的相关性,对系统中谐波潮流进行分析。考虑到风机出力与风速之间呈现非线性关系,风机出力的大小以及分布受风速影响较大。当风速在切入风速与额定风速之间较小时,风机出力近似服从Weibull 分布；当风速接近额定风速时,风机出力偏离Weibull 分布。风速的大小对系统谐波水平分布影响较大,因此设置2 种风速期望场景,分别为场景1（风速期望为7 m/s）与场景2（风速期望为13.5 m/s）,并以风速变异系数为变量反映一定时段内风速的波动程度,分析不同风速场景、不同风速变异系数下所提算法的性能,变异系数取值以5%为步长,范围为5%～20%。以MCS 方法为基准,比较三点估计与Gram Charlier 级数展开（point estimate and Gram Charlier, PEM&GC） 与IMPEM&ME 方法对谐波电压统计特征的估计精度,并通过概率密度函数拟合曲线比较拟合效果。定义相对误差R如下：

式 中：Mo和Mb分 别 为 其 他 方 法（PEM&GC 或IMPEM&ME）和MCS 方法所得的随机变量统计特征。

2 种风速场景下的不同方法所求得的谐波电压幅值统计特征的平均相对误差如图2 所示；以风机与光伏接入节点的谐波电压幅值为例,在相同变异系数（10%）与约束条件下,不同场景下3 种方法的概率密度函数比较如图3 所示。

图2 2 种风速场景下不同方法的谐波电压幅值统计特征的平均相对误差对比Fig.2 Comparison of average relative errors for statistical characteristics of harmonic voltage magnitude with different methods in two wind speed scenarios

图3 不同风速场景下3 种方法概率密度函数比较Fig.3 Comparison of probability density function of three methods in different wind speed scenarios

从图2 可以看出,当风速期望为7 m/s 时,所提方法与PEM&GC 方法所求得的谐波电压的统计特征精确度差距不大。对于谐波电压幅值期望,不同变异系数下2 种方法的平均相对误差均不高于2%；对于谐波电压幅值标准差,2 种方法的平均相对误差均不超过10%。当风速期望达到13.5 m/s 时,2 种方法开始显现出较大差异,随着风速变异系数的增大,二者的平均相对误差均呈现增大趋势。由IMPEM&ME 方法计算得到的统计特征始终比PEM&GC 方法更精确,在变异系数较大时（如20%）,PEM&GC 方法所得标准差的平均相对误差已超过20%,而IMPEM&ME 方法依旧保持较高的准确度。因此,所提算法对风速的变化敏感度较低,在不同风速期望与变异系数下,均能获得较为准确的计算结果。对于2 种算法的概率密度函数拟合性能,不同风速场景下2 种算法所得的概率密度函数曲线均具有一定的拟合效果,其中IMPEM&ME 方法所得的概率密度函数在尾部始终大于零,且更贴近MCS 方法,因此性能更优。相同仿真硬件条件下,MCS 方法耗时最长,而所提方法与PEM&GC方法耗时相当,均具有一定的计算效率。

3.2 基于谐波源监测数据的概率谐波潮流

本节所研究系统与3.1 节中相同,在风机光伏并网节点装有谐波电流监测装置。采用文献［9］中的正态分布描述谐波源监测所得的5 次谐波电流的幅值,均匀分布描述5 次谐波电流相角。选定光伏接入节点的谐波电流相角为参考,风机接入节点发出的谐波电流相角相对节点16 的谐波电流相角在一定范围内均匀分布。在求解过程中,同时考虑谐波电流幅值与相角的不确定性。所研究时段内,5 次谐波电流幅值的期望以及相角相对参考相角分布的最大值θ5,max与最小值θ5,min如附录A 表A2所示。

改变风机节点谐波电流的分布范围,不计谐波源谐波电流之间的相关性,研究基于监测数据直接求解时,不同变异系数下的系统谐波电压相对误差的变化趋势以及概率密度拟合的性能。不同变异系数下系统的5 次谐波电压平均相对误差如图4 所示；以常用变异系数（5%和10%）为例,风机节点的谐波电压的概率密度函数如图5 所示。

图4 不同变异系数下谐波电压幅值统计特征的平均相对误差Fig.4 Average relative errors for statistical characteristics of harmonic voltage magnitude with different variation coefficients

图5 风机节点谐波电压概率密度函数比较Fig.5 Comparison of probability density function for harmonic voltage on bus with wind turbine connected

从图4 可以看出,在该分析场景下,IMPEM&ME 方法获得的统计特征依然具有较高的精度。不同变异系数下,IMPEM&ME 方法所得到的期望的平均相对误差始终低于1%,标准差的平均相对误差低于5%,而PEM&GC 方法所获得的谐波电压标准差的平均相对误差在10%左右。同时,由于谐波电流幅值与相角采用的概率分布与3.1 节中随机变量的概率分布不同,所得的谐波电压的概率密度函数也与3.1 节不同。在所提变异系数下,所得谐波电压呈现近似双峰的分布特点,且谐波电压的分布范围较广。根据图5 概率密度函数拟合结果可以看出,IMPEM&ME 方法所得的概率密度函数较好地反映了谐波电压双峰分布的特点,而PEM&GC 方法难以反映这一特点。由于前期估计误差以及后期拟合的数值积分误差会导致一定的偏差出现,但依旧可反映概率密度函数的尾部特征、最大可能取值等分布特点。3 种方法相比解耦法的计算时间均减少,所提方法效率始终高于MCS 方法。

3.3 谐波电流相关性分析

实际电力系统中,由于相近的用电习惯或外部天气因素影响,功率、谐波电流数据在某一时段的随机变化可能存在一定相关性,这会对系统谐波水平产生一定影响。以3.2 节中系统为例,令谐波源的谐波电流变异系数为10%,假设2 个谐波源所发出的谐波电流幅值存在相关性,其相关系数为0.6,各节点的5 次谐波电压的期望与标准差的平均相对误差Ra、最大相对误差Rmax、最小相对误差Rmin对比结果如表1 所示。

表1 谐波电压幅值统计特征相对误差Table 1 Relative errors of statistical characteristics of harmonic voltage magnitude

对比表1 结果可知,计及相关性时,在谐波电压幅值的期望以及标准差等指标上所提方法相对PEM&GC 方法所得统计特征的估计精度有较大提升。因此,所提方法可较好地处理相关性问题,相比传统方法可更准确地反映系统真实状态。

为反映变量之间的相关性给系统谐波水平带来的影响,以2 个谐波源5 次谐波电流的相关系数r为变量,分析相关性对5 次谐波电压幅值分布的影响。以变异系数为15%为例,不同相关系数下部分节点谐波电压的标准差如图6 所示。

图6 变量相关性对谐波电压幅值标准差的影响Fig.6 Impact of variable correlation on standard deviation of harmonic voltage magnitude

由图6 可知,随着变量相关性的逐渐增强,系统部分节点的谐波电压幅值标准差逐渐减小。统计特征的改变会对输出变量的分布特征产生影响,在实际中可通过所提方法对计及相关性的不确定谐波潮流问题进行准确分析。

4 结语

本文提出一种基于IMPEM&ME 的概率谐波潮流算法。该算法通过采样点的增加,有效提升了待求输出变量统计特征的估计精度；通过引入变量空间变换,提升了计算效率,并可对变量之间的相关性进行研究；引入最大熵概率分布获得更切合实际的概率密度函数。以改进的IEEE 33 节点系统中对所提出的算法的有效性与性能展开研究,结果表明：所提算法在2 种不同谐波潮流分析场景下均表现出较好的适用性,相比目前普遍使用的三点估计与级数展开法所求得的统计特征精度更高,拟合所得的概率密度函数更贴近真实概率密度函数的趋势,可较好地处理与分析随机变量相关性问题。所提方法可帮助运行人员有效分析电力系统不确定谐波状态,以制定合理的谐波治理措施。考虑到概率密度函数拟合精度会受前期估计原点矩误差的影响,下一步将对此展开研究以实现更好的拟合效果。

本文研究得到山东大学青年学者未来计划项目(2016WLJH07)的资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。