弹性体内一类表面波的求解
王 杰 许兰喜
(北京化工大学 数理学院, 北京 100029)
引 言
表面波又叫作瑞利波,这种波在弹性体表面传播,只侵入弹性体内一小段距离,当离弹性体表面很远时,位移趋于零。表面波的发现对地震科学的发展起到了推动作用,不仅可以解释许多地球物理、声学和工程力学现象,而且还具有实际意义,例如应用于地震、石油、地质的勘探,材料的无损探伤,工程结构的抗震抗爆以及岩土动力学等领域。常见的关于表面波的研究有两种方法:一种是解析法,即求解表面波在相应定解条件下的解,该方法大部分都是从直角坐标系出发,导出经典的波动方程从而进行研究;另一种是数值方法,利用有限元、边界元等手段对一些复杂结构中的表面波问题求近似解。Thomson[1]最早提出求解固体介质中弹性波的矩阵方法,之后被Haskell[2]推广到表面波垂直分量的计算中。近年来,针对表面波的研究主要集中在其传播及性质应用方面。如杨天春等[3]采用水平层状介质模型,利用传递矩阵方法推导表面波的质点位移表达式,同时对曲线特征进行分析。柴华友等[4]研究表面源激发的瑞利波的传播特性,比较了激发模态与简正模态相速度的差异。阎守国等[5]利用数值方法研究了半空间表面波的传播和衰减特性,发现通过该特性可以提高表面波勘探的准确性并扩大其应用范围。本文应用解析法对表面波的解进行分析,得到了表面波的一般解。此外,还研究了表面波一般解的结构以及不同行波解波速之间的关系。
1 数学模型
弹性体内的表面波也是一种弹性波,因此满足弹性力学基本方程组[6]
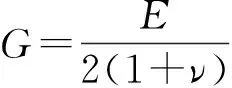
1.1 表面波的平面应变假设
对本文所讨论的弹性体,以y=0为弹性体表面,y轴指向弹性体内,建立如图1所示的坐标系。在平面应变假设下,边界的法向量N=(0,-1,0),弹性体变形为二维的,即U=(u(x,y,t),v(x,y,t),0)。
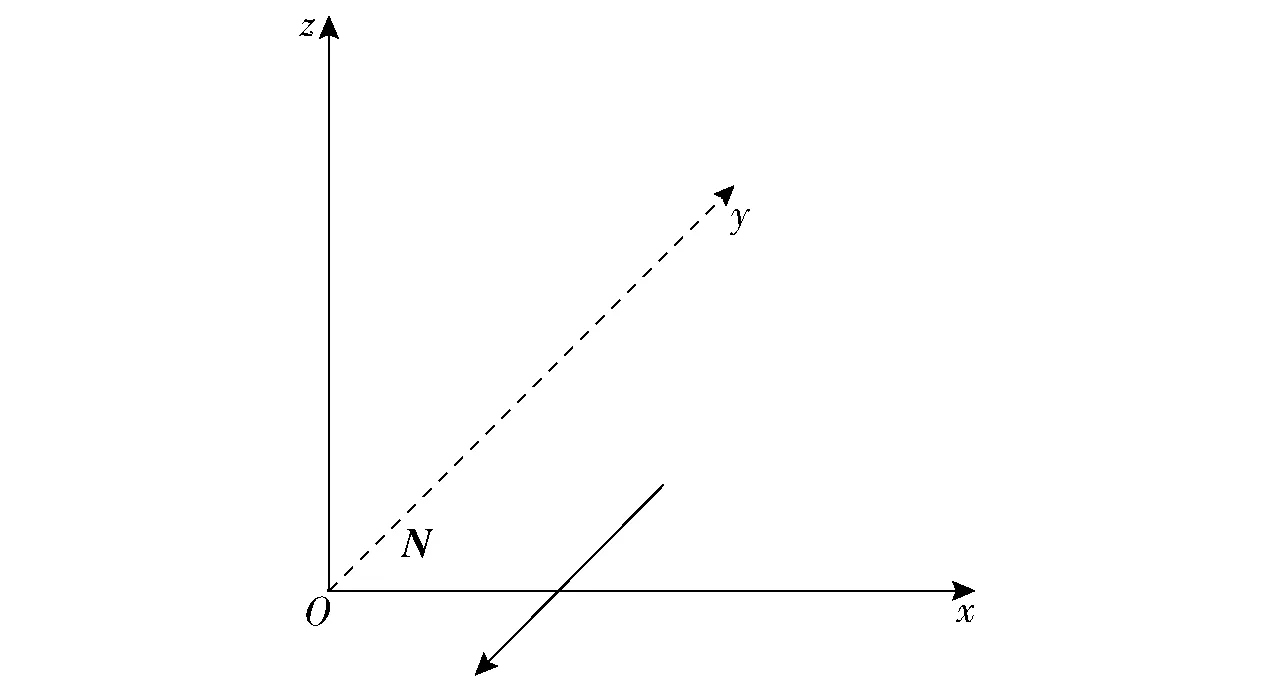
图1 表面波的求解坐标系Fig.1 Solving the coordinate system of a surface wave
由表面波的特性可知表面波满足

(1)
弹性体表面为自由振动,数学表示为
(2)
式中,e为体积膨胀率。
自然边界条件为
(ⅰ)U=U(x,y,t)有界
(3)
(4)
1.2 模型的求解方法
根据向量分析引理,将弹性波分解为膨胀波和畸变波的叠加,即U=U1+U2,分别满足
(5)
和
(6)

2 模型的求解
2.1 膨胀波的解
求解v1,令v1=X1(x)Y1(y)T1(t),代入得X1(x)Y1(y)T″1(t)=a2(X″1(x)Y1(y)T1(t)+X1(x)Y″1(y)T1(t)),两边同除X1(x)Y1(y)T1(t),得到
(7)
先求解本征值问题T″1(t)=pT1(t),步骤如下。

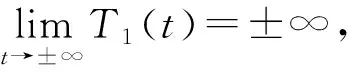
2)p=0,通解为T1(t)=a1+a2t。
(ⅰ)当a2=0时,T1(t)=a1,由自然边界条件(4)可知a1=0。
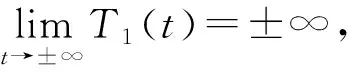
综上,该本征值问题没有p=0的本征值。

T1(t)=a1cos(p1t)+a2sin(p1t)
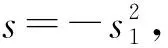
本征值问题Y″1(y)=rY1(y)的求解步骤如下。
1)r<0,通解为
此时不满足条件(1),所以r<0不是该本征问题的本征值。
2)r=0,通解为Y1(y)=c1+c2y。
当c1≠0或c2≠0时,不满足条件(1),所以该本征值问题没有r=0的本征值。
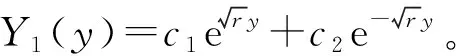

综上,X1(x)、Y1(y)和T1(t)分别表示为
(8)
式中a1、a2、c2、d1、d2均为常数。
将式(8)代入v1=X1(x)Y1(y)T1(t),得
v1=c2e-r1y(d1cos(s1x)+d2sin(s1x))(a1cos(p1t)+a2sin(p1t))
(a1cos(p1t)+a2sin(p1t))+C1(x,t)
故u1,v1分别为
(9)
式中C1(x,t)是关于x,t的函数。
又由式(7)可得
(10)
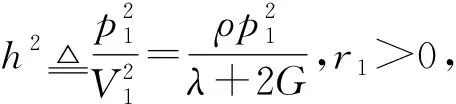
2.2 畸变波的解
(11)
式中C2(x,t)是关于x、t的函数,且有
(12)

2.3 表面波的解
将式(9)、(11)这两个解叠加得
(13)
式中φ1、φ2、φ3和φ4都是关于x,t的函数。
由式(1)得
所以C1(x,t)=0,C2(x,t)=0。
利用C1=C2=0,则式(13)变为
(14)
将式(14)代入式(2)中第一个式子,可得当y=0时有
(15)
下面证明s1=s2。由于系数c2,c′2,di,d′i,ai,a′i具有任意性(i=1,2),不妨取c2=c′2=1,d1=-d′2=0,d2=d′1=1,a1=a′1=1,a2=a′2=0。
则式(15)变为
k1cos(s1x)cos(p1t)+k2cos(s2x)cos(p2t)=0
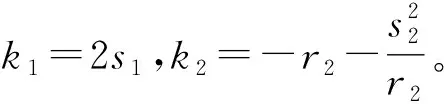
k1cos(s1x)+k2cos(s2x)=0
又k1=2s1≠0,可得cos(s1x)、cos(s2x)线性相关,由此有s1=s2。同理可得p1=p2。
利用s1=s2,式(15)变为
(16)
下面证明对任意的x,t都有φ1(x,t)=φ2(x,t)。
由系数的任意性,不妨令
将式(14)代入式(2)中第二个式子,同理得φ3=φ4。
将φ1=φ2,φ3=φ4和s1=s2代入式(14)得
(17)
将式(17)代入式(2)可得
(18)
求解式(18)即可得表面波的解。
3 解的性质
3.1 解的波速
虽然表面波的解不唯一,但是其波速并不会随解的不同而发生改变,下面证明这一性质。从一般解式(14)入手,将式(14)代入式(2),得到式(18),发现与变量x、y、t有关的项全部被消除了,只与常数r1、r2、s1、c2、c′2有关,因此不妨预测不同解的波速是相同的。
由式(18)得
(19)
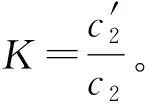
可得
将K代入式(19)中第一个式子,有
(20)
(21)
式(21)的求解参考文献[1]。由式(21)可得α的值只与ν有关,当ν取定时,α为定值。当ν=0.25时,可得α=0.919 4,则波速
(22)
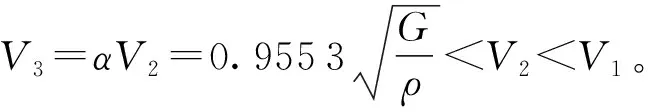
由式(22)可知,α确定后,表面波的波速只与剪切弹性模量G和弹性体的密度ρ有关。当这两个量固定时,表面波所有行波解的波速是相等的,并且与文献[1]所求右行波解的波速吻合。
同时,还可以得到弹性体内膨胀波、畸变波和表面波的速度大小关系为V3 (23) 对式(23)利用积化和差公式,得 式中l1、l2、l3、l4和h1、h2、h3、h4分别为 易证h1,h2,h3,h4线性无关。 事实上,由k1h1+k2h2+k3h3+k4h4=0,通过取x,t分别为0,联立解得k1=k2=k3=k4=0。 综上,可得解的结构为 (24) 式中,ξ∈span{h1,h2,h3,h4},a′∈span{e-r1y},b′∈span{e-r2y}。 由此可知解有3种可能,即左行波、右行波或者左右行波的叠加。特别地,当l2=1,l1=l3=l4=0时,得到了文献[1]所给的右行波解。 本文基于弹性力学基本方程组和向量分析引理,利用分离变量法,分别得到了满足条件的膨胀波和畸变波的解,通过叠加最终得到表面波的一般解。在对一般解的分析中得到的结论如下。 (1)表面波的解不唯一。它的一般解的结构为 其中ξ∈span{h1,h2,h3,h4},a′∈span{e-r1y},b′∈span{e-r2y}。 这些行波解可能为左行波,也可能为右行波,还可能为左右行波的叠加。 (2)当ν取定时,表面波不同解的波速只与弹性体密度ρ和剪切弹性模量G有关。膨胀波、畸变波和表面波的速度大小关系为V33.2 解的结构

4 结论

