概周期系数的时滞广义系统概周期解的存在性

黄记洲

(1.广东清远职业技术学院；2.广东清远开放大学，广东 清远 511510)

1 引言与研究背景

生物数学模型与微分方程有着密切的关系，以微分方程建立的生物系统往往有其特性，即周期性和概周期性，因此，研究微分方程的解的周期性和概周期性有着极其重要的意义。近年来有不少的专家学者对微分方程的概周期解的存在性作了研究，得到了满意的结果。如文献[1-3]。

文献[4-5]黄建吾、孟艳双等分别以指数型二分性及Schauder不动点定理研究了微分方程组

周期解和概周期解的存在问题，并得到此类微分方程组的周期解和概周期解存在的充分性条件。

文献[6]运用二分性及Schauder不动点定理，研究一类时滞概周期系数的五次微分方程组

并得到了此类微分方程概周期解存在的充分条件。

对于广义系统

(1)

当常量m≥1的整数，τ∈R,变量t∈R，a(t),b(t),c(t),d(t)都是概周期函数，f(t,y),g(t,y)定义在R2上的连续函数且对y∈R关于t的一致概周期函数。此系统是否也有概周期解呢？下面我们就研究这个问题。

定义1[7]设线性系统

x′=A(t)x

(2)

这里A(t)是定义在某区间J上的连续矩阵函数，常见的情况为J=R+,R-或R，若存在投影矩阵P和k>0，α>0，β>0的常数，使得线性系统(2)的基解矩阵X(t)对任意s,t∈J满足

|X(t)PX-1(s)|≤kexp(-α(t-s)),t≥s,

|X(t)(E-P)X-1(s)|≤kexp(-β(s-t)),s≥t,

则称线性系统(2)在J上满足指数型二分性。

引理1[8]线性系统(2)有指数型二分性，A(t)是概周期矩阵函数，f(t)∈AP(En)，则非齐次线性系统x′=A(t)x+f(t)有惟一界周期

引理2[9]设fn(t)(n=1,2,3…)为区间I上可微的函数族，若{fn′(t)}在I上一致有界，则{fn(t)}在I上等度连续。

引理3[10](Ascoli定理)若{fm(t)|fm:R→Rn}(m,n=1,2,3…)一致有界，等度连续。则{fm(t)}必存在子列{fmk(t)}在任意有限区间上一致收敛。

引理4[10](Schauder不动点定理)设B是Banach空间中的有界闭凸集，若T:B→B连续，且TB紧致，则T在B上必有不动点。

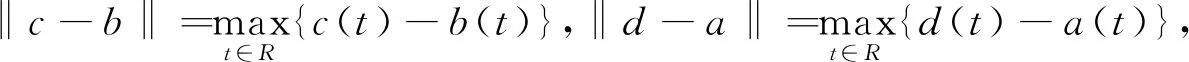
2 主要结论

定理1设系统(1)满足下列条件：

(Ⅰ)f(t,y),g(t,y)定义在R2上的连续函数，对y∈R关于t的一致概周期函数，且分别满足Lipschitz条件。即存在正常数L1,L2，对于任意(t,y1),(t,y2),(t,y3),(t,y4)∈R2使得

|f(t,y1)-f(t,y2)|≤L1|y1-y2|,|g(t,y3)-g(t,y4)|≤L2|y3-y4|

则方程(1)存在概周期解。

现把(1)化为

x′=a(t)x-c(t)ym+1+[c(t)-b(t)]ym+1+f(t,y(t-τ))

y′=c(t)xym+a(t)y+[d(t)-a(t)]y+g(t,y(t-τ))

对于任意h(t)∈B1,我们考虑线性系统

x′=a(t)x-c(t)[h(t)]my+[c(t)-b(t)][h(t)]m+1+f(t,h(t-τ))
y′=c(t)[h(t)]mx+a(t)y+[d(t)-a(t)]h(t)+g(t,h(t-τ))

(3)

其齐次系统

x′=a(t)x-c(t)[h(t)]my

y′=c(t)[h(t)]mx+a(t)y

(4)

可以找出它的基础解系

当t≥s时有

由定义1，系统(4)具有投影为P=E(单位矩阵)的指数型二分性。由引理1得系统(3)有唯一概周期解

我们作一个映射T：B1→B1，Th(t)=yh(t)

(ⅰ)∀h(t)∈B1

所以Th(t)∈B1即TB1⊂B1

(ⅱ)T是紧致的。事实上,对于任意hn(t)∈B1,记yhn(t)=Thn(t)，则

即yhn(t)一致有界。考虑

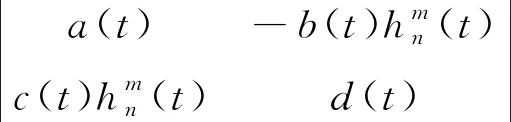
(ⅲ)T是连续的．事实上,对于任意

考虑

所以

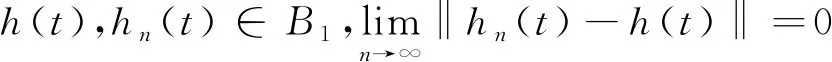
hn(t-τ)→h(t-τ)，明显地，当n→∞时，有|Thn-Th|→0，因此T是一个连续的算子。

由引理4(Schauder不动点定理)知，系统(3)有不动点，记为h(t)。由h(t)=Th(t)=yh(t)有

注：当m=4时，就是文献[6]的系统，因此，定理1推广了文献[6]的定理1。

定理1的条件可以进一步减弱，可不要求f(t,y),g(t,y)对y∈R关于t的一致概周期函数，便得到下列定理。

定理2设系统(1)满足下列条件：

(Ⅰ)f(t,y),g(t,y)定义在R2上的连续函数并有f(t,0)=g(t,0)=0，且分别满足Lipschitz条件。即存在正常数L1,L2，对于任意(t,y1),(t,y2),(t,y3),(t,y4)∈R2使得

|f(t,y1)-f(t,y2)|≤L1|y1-y2|,|g(t,y3)-g(t,y4)|≤L2|y3-y4|；

则系统(1)存在概周期解。

定理2的证明与定理1相类似，所以这里就不再赘述了。

注这个结论推广了文献[6]的定理2。

3 结语

本文运用二分性、不动点定理等理论，研究概周期系数的时滞广义系统概周期解的存在性，得到此系统的概周期解存在的充分性定理，推广和丰富了文献[4-6]的结果，理论上解决了具有时滞的生物系统在某一状态变化问题。当系统(1)第二个方程的d(t)y的变为d(t)ym,其他项不改变，这样的系统是否也存在概周期解，如果存在，它的充分性定理是怎样的呢？这是可以进一步研究和探讨的问题。