对称因子表的快速形成及直角坐标和极坐标PQ分解法的比较
陈 恳,丁 戈,3,唐婧璇,万新儒
(1.南昌大学信息工程学院,江西 南昌 330031;2.江西电力职业技术学院,江西 南昌 330032;3.国网睢宁县供电公司,江苏 徐州 221200)
因子表法一般用于求解常系数线性方程[1-7]。不少文献提及求取因子表时一般均采用“按行消元,逐行规格化”的过程[1,5]。对于对称矩阵,按行消元的方式并不利于根据元素的对称性进行计算。文献[1-2]虽提及利用对称性简化下三角元素计算,或仅存储和计算上三角元素。但在按行消元的前代计算中,获取下三角元素并不方便,而仅存储和使用上三角元素也会增加对对角元的反复乘除计算。此外,文献[1-6]中都是在形成因子表后再对对角元取倒数,无形增加了程序的除法运算,降低了计算速度。
在牛顿-拉夫逊法(牛顿法)潮流计算基础上发展起来的PQ分解法(PQ法)是电力系统中广泛使用的潮流计算方法,其特点是将牛顿法潮流中变系数、不对称的雅可比矩阵简化成常系数、对称的系数矩阵,从而将有功无功分开迭代[1-8]。然而当系统中有PV节点时,直角坐标牛顿法的方程数多于极坐标牛顿法,且前者的潮流迭代次数有时也会多于后者。但在实际潮流计算中,一般前者的计算速度快于后者,主要原因是受后者三角函数计算的影响[12]。受极坐标牛顿法的修正方程数及潮流迭代次数均少于直角坐标牛顿法等表象的影响,极坐标PQ法的应用极为广泛,而直角坐标PQ法几乎没有被介绍和应用。
本文对传统因子表的形成过程进行改进,包括:规格化前就对对角元取倒,而不是在形成因子表后才将对角元取倒;采用逐行规格化按列消元的方式、利用对称矩阵的特点按对称算法形成因子表。分别将这些方法用于IEEE-30~-118节点系统,可大大减少因子表的形成时间,提高计算速度。
通过比较系统中PV节点数、方程数、三角函数等对潮流迭代次数和计算速度的影响,对直角坐标和极坐标PQ分解法的计算原理进行了详细地对比分析可发现,尽管极坐标PQ法中的方程数和迭代次数均少于直角坐标PQ法,但由于前者三角函数的计算,其潮流计算速度仍比后者慢很多。
1 对称因子表法
1.1 按行消元形成因子表的问题
设n阶线性方程组为AX=F。传统因子表法对A阵采用“按行消元,逐行规格化”,对第k行元素消元后的A(k)′阵为式(1)。
(1)

(1)第1~k-1各行中仅一个元素与第k行中ak1~ak,k-1的一个元素对应,其对应元素的寻找、行列的变化均过于复杂。
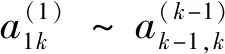
(3)由于在形成整个因子表后才将所有的对角元取倒,在其规格化计算式如式(2)中仍然有不少除法计算而影响计算速度。
(2)
1.2 按列消元形成因子表的优势
如果对A阵采用“逐行规格化,按列消元”,且在每行元素规格化前将对角元取倒,则对第k列元素消元后得的A(k)′阵为式(3)。
(3)

(4)
(5)
比较“按行消元,逐行规格化”和“逐行规格化,按列消元”的计算过程可看出,后者在对应元素的寻找、程序中行列的变化以及元素对称性的应用上均有极大的优势。如果再考虑元素规格化前将对角元取倒,则还可进一步提高计算速度。实际上,在形成因子表后对F阵的前代过程中,不少文献均采用按行消元的计算方式[4],如果该过程也用按列消元方式,同样可大大提高计算速度。
1.3 对称因子表法
根据式(3)可看出,“逐行规格化,按列消元”是用第k行对角元及其以右的元素对对角元以下元素进行消元。而对对称矩阵,其第k行对角元以右的元素与第k列对角元以下的元素仅相差其对角元。因此,在形成因子表的消元计算过程中,可仅计算上三角元素,而将规格化前对角元以右元素赋值给对角元以下相应的元素获得下三角元素。
根据上述计算规律,对称因子表的形成过程可归纳如下:
(1)将对第k行规格化前的元素赋值给第k列对角元以下的元素,再将对角元取倒后对第k行规格化,然后对第k列元素消元,且仅计算各行中的上三角元素;
(2)将对第k+1行规格化前的元素赋值给第k+1列元素,再将对角元取倒后对第k+1行规格化,再对第k+1列元素消元,且仅计算各行的上三角元素;
(3)依此循环。
对称因子表法是通过规格化前的上三角元素赋值得到,因而可省去所有下三角元素的计算,并由于对角元在规格化前取倒,可大大减少规格化的除法计算,从而加速因子表的形成。
1.4 对称因子表法中四角规则应用
用四角规则可直接完成消元的前代计算而无需应用消元计算公式[13],大大简化程序的编制。
对第k列元素消元前后其简化矩阵如图1所示。

用四角规则只要根据相应元素在矩阵中的位置就可直接写出计算元素的表达式,而无需使用消元计算公式。且在对称因子表法中,只需计算所有的上三角元素,其下三角元素可通过规格化前的元素直接赋值得到。四角规则可大大简化编程计算。
2 极坐标与直角坐标PQ法的比较
2.1 极坐标PQ法
极坐标PQ法修正方程如式(6)、(7)。
[ΔP/V]=[B′][VΔδ]
(6)
[ΔQ/V]=[B″][ΔV]
(7)
展开式(6)、(7)可得
(8)
(9)
2.2 直角坐标PQ法
直角坐标牛顿法修正方程式如式(10)。
(10)
由于电力网络中各元件的电抗x远大于电阻r,因此有功功率Pi变化主要受电压虚部fj影响,无功功率Qi和电压幅值Vi变化主要受电压实部ej影响,为此可略去式(10)中N、M、R子阵。再根据fi≪ei、Gij≪Bij,可得Gijfi≈0,并忽略接地支路。对式(10)中H、L、S子阵简化后可得直角坐标PQ法修正方程如式(11)、(12)。
[ΔP/e]=[B′][Δf]
(11)
(12)
展开式(11)、(12)可得式(13)、(14)
(13)
(14)
2.3 极坐标与直角坐标PQ法的比较分析
虽然极坐标与直角坐标PQ法的计算原理接近,但仍有以下几点主要不同:
(1)比较式(8)、(9)和式(13)、(14)可看出,与牛顿法类似,极坐标PQ法的方程数比直角坐标PQ法更少。
极坐标PQ法的式(8)、(9)中,B′阵为(n-1)阶,B″阵为m阶,且均为对称阵;直角坐标PQ法的式(13)、(14)中,B′阵和B″阵均为(n-1)阶,前者为对称阵,后者为不对称阵。
(2)虽然直角坐标PQ法的式(14)中阶数为(n-1)阶,但由于其与PV节点对应的方程中仅其对角元为-2,其它元素均为零。因此式(14)中可只对第1~m个方程消元,而对第m+1~n-1个方程无需消元。因此可将式(14)方程简化为式(15)。
(15)

(3)分别比较式(8)、(9)和式(13)、(15)可看出,直角坐标PQ法的有功迭代过程略简单,极坐标PQ法的无功迭代过程略简单。
(4)极坐标PQ法中在节点电流或节点功率的计算中需使用大量三角函数,而直角坐标PQ法没有。

3 算例分析
不考虑稀疏性时,对IEEE-30~-118节点系统用传统因子表法、规格化之前先对对角元取倒的改进因子表法以及对称因子表法形成因子表时间的比较结果如表1;且在均用对称因子表法时,直角坐标PQ法和极坐标PQ法潮流的收敛时间、迭代次数等比较结果如表2。收敛判据均为ε≤10-5。

表1 不同因子表法形成时间的比较

表2 PQ法潮流计算时间和迭代次数的比较
根据表1可看出,与传统因子表法相比,在规格化之前先对对角元取倒的改进因子表法形成因子表的速度对各个系统均可提高约4%,而用对称因子表法形成因子表的速度随着系统规模的增加而增加。如对IEEE-30节点系统其速度可提高约20%,而对IEEE-118节点系统可提高约35%。
根据表2可看出,虽然极坐标PQ法的迭代次数一般均少于直角坐标PQ法的迭代次数,但由于直角坐标PQ法中无三角函数的计算,其收敛所需时间反而比极坐标PQ法少很多。如IEEE-118节点系统,极坐标PQ法的迭代次数为6/5,直角坐标PQ法的迭代次数为9/8;但直角坐标PQ法收敛的计算时间仅为极坐标的32.84%,且该优势随着系统规模的增加而增加。因此,直角坐标PQ法比极坐标PQ法可能有更好的应用前景。
4 结论
本文在规格化之前将对角元取倒,可进一步减少除法计算;利用元素对称性,仅计算上三角元素,下三角元素按列通过赋值上三角规格化前的元素得到,可大大提高因子表的形成速度;用四角规则可直接完成相应的消元计算,而无需应用消元计算公式,极大地便于编程。提出直角坐标PQ法,尽管其与常用的极坐标PQ法相比需求解的方程数和迭代次数更多,但由于对其方程采用特殊解法,且没有三角函数计算,因此与极坐标PQ法相比,其潮流计算速度大大加快。且随着系统规模的增加,优势更加明显。

