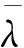一种严格成立的惩罚函数法及其求解
侯小秋
(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
0 引 言
惩罚函数法求解约束最优化问题,将问题的目标函数与约束函数构造增广目标函数,即惩罚函数,将约束最优化问题转化为无约束最优化问题求解。根据惩罚函数构造的思想不同,分为内点惩罚函数法[1]、外点惩罚函数法[2]和混合惩罚函数法[3],还可分为静态惩罚函数法[4]、动态惩罚函数法[4]、退火惩罚函数法[4]和自适应惩罚函数法[4]。各种惩罚函数法都有自己的优缺点。笔者分析一种外点惩罚函数法[2]解析解和数值解在可行域内成立的条件,针对具有偏置量的外点惩罚函数法,同样分析其数值解和解析解在可行域内的条件,当偏置量满足允许误差限的限制条件时,偏置量外点惩罚函数法具有严格成立性,提出一种高数值稳定性的改进DFP拟牛顿法,应用文中求解偏置量外点惩罚函数法。
1 外点惩罚函数法
1.1 解析解
一般约束最优化问题为
式中:x——优化变量;
f(x)——优化函数;
gj(x)——等式约束;
cm(x)——不等式约束。
构造惩罚函数[2]为
(1)
式中:F(…)——惩罚函数;
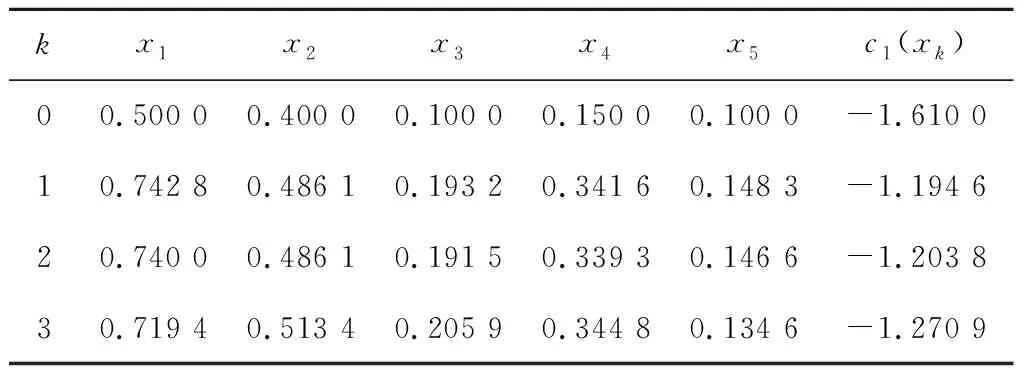
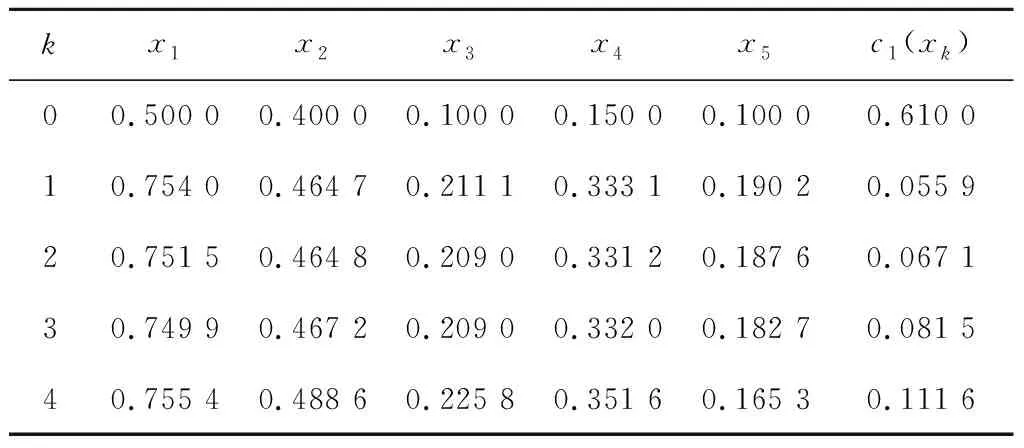
M(k)——惩罚因子,且有,0 式(1)的解析解x*为 (2) 由式(2)求得的x*,若 cm(x*)≤0,m=1,2,…,M。 (3) (4) 则,解析解x*在可行域外,外点惩罚函数法解无效。 数值解可采用无约束最优化的最速下降法和牛顿法及拟牛顿法等求解,当 cm(xk+1)≤0,m=1,2,…,M, (5) 式中:xk+1——k+1步数值解; k+1——迭代步数。 (6) 则,数值解在可行域外,外点惩罚函数法解无效。 在文献[2]的外点惩罚函数法的惩罚函数中加入偏置量,构造惩罚函数为 (7) μ——偏置量,μ>0。 针对式(7)求解可构成偏置量外点惩罚函数法,由式(7)可得其解析解为 同样,具有式(3)、(4)的解,在可行域内或可行域外的问题。 分析表明,其数值解形式与式(5)、(6)一致的结论。 令 fm(x,μ)=cm(x)+μ。 (8) 选取终止条件为 f1(xk+1,μ),…,fM(xk+1,μ)‖p≤ε, (9) 式中:ε——允许误差限,ε>0适当正数; ‖…‖p——范数,p=1或2。 则由式(9)得 -ε1/p≤fm(xk+1,μ)≤ε1/p。 (10) 将式(8)代入式(10)得 -ε1/p≤cm(xk+1)+μ≤ε1/p, (11) 则由式(11)得 -ε1/p-μ≤cm(xk+1)≤ε1/p-μ, 选取 μ≥ε1/p, (12) 则有 cm(xk+1)≤ε1/p-μ≤0。 (13) 满足不等式(13)约束,偏置量外点惩罚函数法的严格成立。可采用无约束最优化的最速下降法[5]、修正牛顿法[6]、共轭梯度法[7]和拟牛顿法[8]等算法求解,文中采用改进的DFP拟牛顿法求解。 文献[9]的DFP拟牛顿法的迭代矩阵为 Hk+1=Hk+ΔHk, (14) 式中:Hk——近似矩阵; ΔHk——校正矩阵。 (15) 式中:Zk——近似解增量; Yk——梯度增量。 且 Zk=xk-xk-1, Yk=∇f(xk)-∇f(xk-1), 式中:f(…)——目标函数; ∇f(xk)——梯度。 Hk+1应满足的拟牛顿条件 Hk+1Yk=Zk, (16) 将式(14)代入式(16)得 ΔHkYk=Zk-HkYk。 (17) 文献[9]的DFP校正公式为 改进为 (18) 式中:λ1——权重矩阵; λ2——辅助矩阵。 式(18)右乘Yk得 (19) 比较式(19)和式(17)得 (20) (21) 由式(21)得 (22) 可取 (23) 令 Uk=αk(Zk+δ1Yk), (24) Vk=βk(HkYk+δ2Yk), (25) 式中:δ1——权重因子; δ2——权重因子; αk——加权因子; βk——加权因子。 由式(24)代入式(20)得 (26) 由式(26)可得 由式(25)代入式(23)得 (27) 由式(27)得 由文献[6]可知, 当Yk不是零向量时,只要适当选取δ1和δ2,即可使αk和βk的分母不趋于零,提高了算法的数值稳定性。 式(24)、(25)、(22)代入式(18),再代入式(14)、(15)得 (28) 由式(28)可知,Hk+1不对称,要使改进的DFP拟牛顿法有效,需保证Hk+1广义正定,由文献[11]的引理2,若Hk+1广义正定,其对称分量 正定。 式中:n——SA的维数; SA(i,j)——SA的元素。 式中,b——适当的正数。 下面讨论式(28)的2个简化算法。 算法1 λ2=λ3Hk, 式中,λ3——对角矩阵。 算法2 δ1=δ2=0, λ2=λ4Hk, 式中,λ4——加权因子。 则,式(28)退化为 (29) 下面证明式(29)的算法,因引入加权因子λ4,可提高算法的数值稳定性。此时,Hk+1对称,引入Hk=QTQ,Q非奇异矩阵,代入式(29)得,∀Y∈Rn,且Y≠0,有 YTHk+1Y=YTHkY(1+λ4)+ 记QY=w,QYk=q,则 (30) 选取λ4>0,则式(30)的第二项与文献[13]的证明扩大1+λ4倍,加强了算法的数值稳定性。 由式(7)可得 (31) 则 (32) 式(31)、(32)代入式(28)求解 待优化问题 s.t.g1(x)=x2+x4-x5-1=0, g2(x)=x1+x2+x3+x4+x5-2=0, g3(x)=2x1-0.5x3+x4-x5-1.5=0, 初始化x1(0)=0.5,x2(0)=0.4,x3(0)=0.1,x4(0)=0.15,x5(0)=0.1。选取ε=1M(k)=2×1.1k,H0=I,λ2=diag[2,3,4,3,2]。 采用Matlab软件编程实现数值分析,选取μ=ε1/2=1,严格成立的具有偏置量的惩罚函数法的优化过程如表1所示。由表1可知,在优化步骤k=3时,得优化解,且c1(x3)=-1.270 9<0,不等式约束满足,其最优解合理有效。选取μ=0.1,具有偏置量的惩罚函数法的优化过程如表2所示。 表1 严格成立的具有偏置量惩罚函数法的优化过程 表2 具有偏置量的惩罚函数法的优化过程 由表2可知,在优化步骤k=4时停止优化,此时,c1(x4)=0.111 6>0,不等式约束不满足,其最优解也是不合理的无效。 (1)理论分析表明,外点惩罚函数法和具有偏置量的外点惩罚函数法其解析解和数值解有时不满足不等式约束。当偏置量和允许误差限满足式(12)时,具有偏置量的外点惩罚函数法得数值解满足不等式约束,严格成立。 (2)在DFP拟牛顿法的校正公式中引入辅助矩阵和权重矩阵,获得了改进的DFP拟牛顿法,式(24)、(25)对Uk和VK进行改进,使αk和βk的分母中引入了δ1‖Yk‖2和δ2‖Yk‖2项,合理地选取δ1和δ2,可使αk和βk的分母不趋于零,提高了算法的数值稳定性。给出了改进后DFP拟牛顿法的两个简化算法,其简化算法2具有提高算法数值稳定性的性能。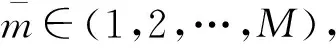
1.2 数值解
2 偏置量外点惩罚函数法
2.1 解析解
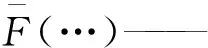
2.2 数值解
2.3 偏置量外点惩罚函数法的严格成立

3 改进的DFP拟牛顿法
3.1 改进的DFP拟牛顿法的推导

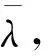
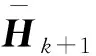
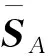

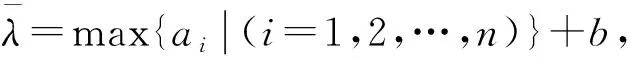
3.2 改进的DFP拟牛顿法求解
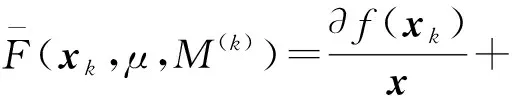
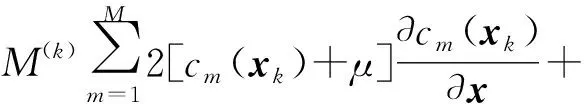

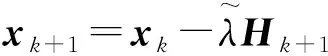

4 算例的数值分析
5 结 论