基于GeoGebra的数学探究性活动设计
——以“瓜豆原理”的教学为例

翟小芳 (江苏省江阴实验中学 214433)

动点问题涉及图形变换，学生往往很难看到动点之间的变换、路径之间的联系，动点问题也是当下中考的一热门话题，此类问题又以所谓的“瓜豆原理”模型为典型．笔者带领学生围绕具体问题，以GeoGebra(简称GGB)为平台开展了一次数学探究之旅，在挖掘问题的教育价值的同时，帮助学生从图形变换视角认识并归纳动点运动问题的本质．

1 过程实录

1.1 创设情境，聚类分析

出示两个问题，并演示其动图，教师引领学生思考问题解决策略．

图1 图2

问题2(2019年宿迁中考)如图2，正方形ABCD的边长为4，E为BC上一点，且BE=1，F为AB边上的一个动点，连结EF，以EF为腰向右侧作等边△EFG，连结CG，则CG的最小值为．

两问题均属于典型的动点问题.以问题1为例，点F因点E的变化而变化(通常称F为“从动点”、E为“主动点”)，要求出OF的最小值便需追踪动点F的轨迹，而从动点的轨迹显然取决于主动点的轨迹和图形变换规则(将E绕D顺时针旋转90°后得到点E′，再将E′点以D为中心缩放一半得到点F)，而这种“旋转+位似”的变换恰是我们需要重点关注的模型．

设计意图与文[4]的设计相区别的是，我们不是简单地将探究任务抛给学生，而是从具体实际问题出发，在动点间依存关系的具体分析中，聚类提炼出需要探究的具体任务，即“旋转+位似”的变换模型．

1.2 尝试探究，形成命题

(1)创建角度滑动条α(范围0～π)和数值滑动条t(范围0～5)，构造两点A,P，输入指令“位似(旋转(A,α,P),t,P)”得到从动点B，构造线段PA,PB；

(2)任意构造点C,D，输入“圆周(C,D)”得到圆f，修改主动点A的属性为“描点(f)”，输入指令“轨迹(B,A)”，得到从动点B的运动轨迹loc1，拖动滑动条改变参数α,t的值，可以发现轨迹loc1始终为圆(图3)；

图3 图4

(3)输入“直线(C,D)”得到直线g，修改主动点A的属性为“描点(g)”，可以发现从动点B的运动轨迹loc1变为了直线，而拖动滑动条改变参数α,t的值，轨迹loc1始终为直线(图4)；

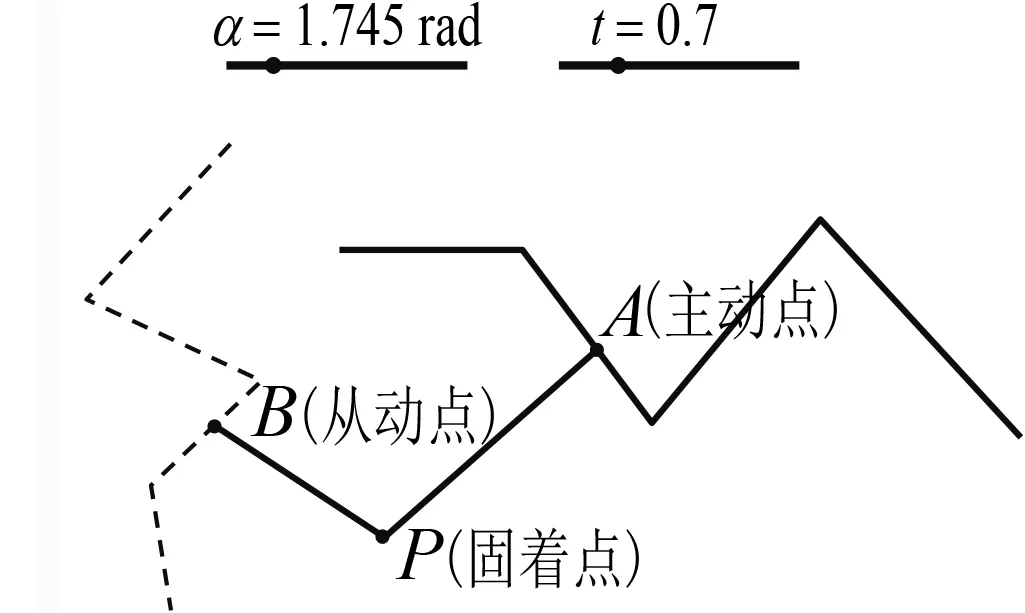
图5

(4)任意构造点E,F,G,H，输入“折线(E,F,C,G,H)”得到折线h，修改主动点A的属性为“描点(h)”，可以发现从动点B的运动轨迹loc1变为了折线，而拖动滑动条改变参数α,t的值，轨迹loc1始终为折线(图5)．

从上述实验探究结果可以发现，从动点轨迹与主动点轨迹相似；正如“种瓜得瓜，种豆得豆”，这儿可是“种”圆得圆，“种”线得线，于是不难归纳出可谓之“瓜豆原理”的如下命题：如图3～5，已知P为定点，A,B两点为动点，在运动过程中始终有∠APB=α,PA=tPB；若点A在曲线Γ(圆、直线、折线等)上运动，则点B的运动轨迹T与曲线Γ相似．简而言之可概括为：一条折线段，固定其折点；邻边定比例，夹角不改变．主动于直线，从动于直线；主动于圆(弧)，从动于圆(弧)．

设计意图将所谓“瓜豆原理”的结论寓于实验、观察、探究中，在此过程中不仅有结论的发现，更有规则的强化，通过“旋转+位似”的表达，演绎运动轨迹的相似，而这恰是证实的基础．

1.3 正本清源，证实命题

通过前面的实验探究，我们已经确信从动点B的运动轨迹T与主动点A的运动轨迹Γ相似，即“种”圆得圆、“种”线得线，那么如何证明呢？考虑到旋转变换不改变曲线形状，而位似变换说明相似，因此命题的证明可以从三角形的相似角度加以证实．

图6 图7

当曲线Γ为圆时，设圆心为C、半径为r；如图6，构造圆心C的旋转位似变换点D．由PA=tPB，PC=tPD，∠APB=∠CPD=α⟹∠APC=∠BPD=α-∠CPB．证得△APC∽△BPD，从而有BD=tAC=tr，即点B在以D为圆心、tr为半径的定圆上运动．当曲线Γ为直线时，如图7，作PA0⊥Γ于点A0，构造点A0的旋转位似变换点B0，设直线AA0,BB0相交于点Q．易证△APA0∽△BPB0，所以∠AA0P=∠BB0P=90°；于是四点P,A0,Q,B0共圆，故而∠A0QB0=π-∠A0PB0=π-α．从而证得点B在定直线T(与直线Γ的夹角为α或π-α)上运动．

设计意图数学中讲究“大胆猜想、小心求证”，在求证过程中可以触及数学问题的本质.事实上，旋转改变位置、位似改变大小，这正可以在命题证明的过程中帮助学生理解“旋转+位似”的涵义．

1.4 应用模型，彰显实效

当我们认识了“瓜豆原理”，便可以由主动点的运动轨迹得到从动点的运动轨迹，继而从整体上解决相关的运动路程求解及线段最值问题.这样上课伊始给出的两个问题便可轻松得到解决．

问题1主动点E的轨迹为半圆弧，故而从动点F的轨迹也为一个半圆．

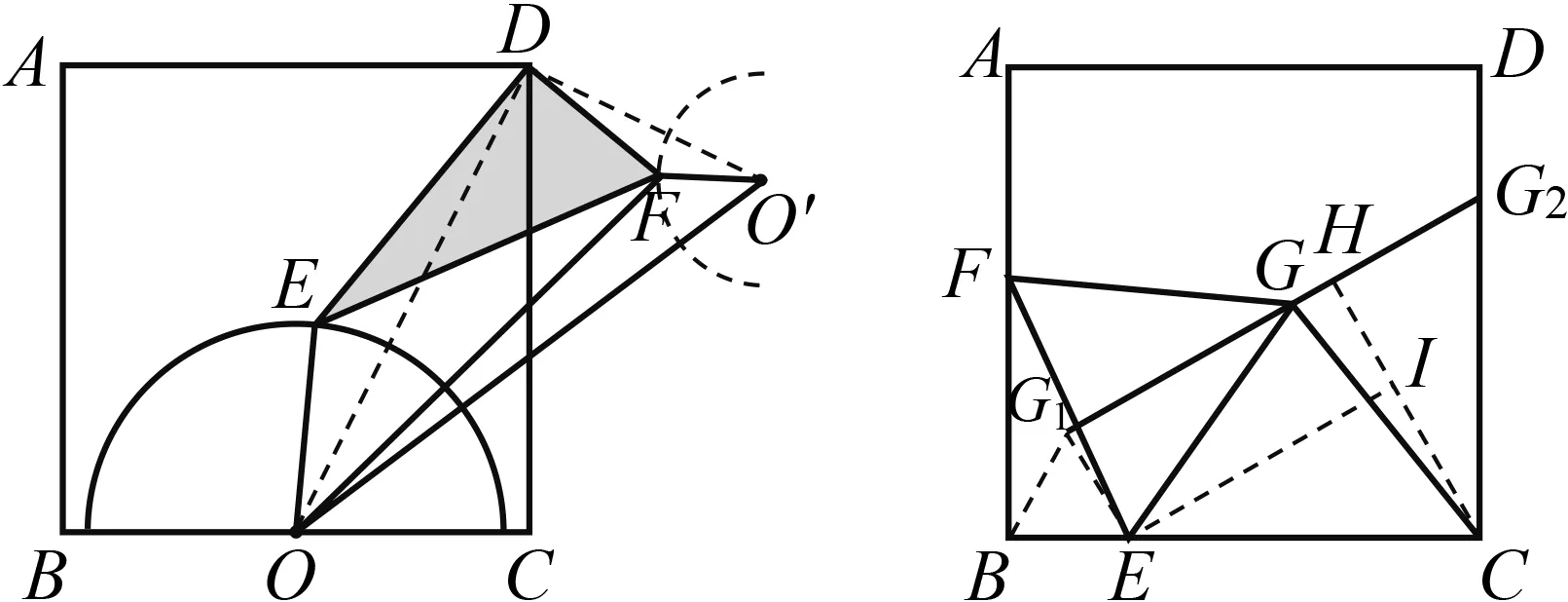
图8 图9

问题2主动点F的运动轨迹为线段AB，则点G的运动轨迹也是一线段(长度与AB相等)．

如上两例是当前中考试题和中考模拟试题中的热点和难点，其实质是旋转(全等)变换，以“瓜豆原理”为指向，使解决问题的思路变得简约通畅．

图10

例如图10，AB=4，O为AB的中点，⊙O的半径为1，P是⊙O上一动点，PC⊥PB(点B,P,C顺时针方向排列)且满足PC=tPB，则线段AC的取值范围为．

2 教后反思

随着新一轮课程改革的逐步深入，如何帮助学生“用数学的眼光、视角发现问题，用数学的语言、模型描述问题，用数学的思想、方法解决问题”，已成为摆在数学教育人面前的共同课题．开展数学探究性活动，在经历“数学化”的过程中深入思考学科问题，可引领学生的数学思维从表层进入深层，在其内心深处培植理性的种子．

2.1 探究活动——深度教学的重要课题

核心素养时代，要求我们的数学教学必须超越表层的符号教学，在准确把握学科本质的基础上触动学生情感和思维的深处，即“通过数学学会思维”，这其实就是深度教学．类似于本节课开展的数学探究活动，围绕某些具体问题(问题1、问题2)，从共性角度发现和提出有意义的数学问题(“旋转+位似”动点问题)，通过动态观察猜测出合理的数学结论(种瓜得瓜、种豆得豆)，开展自主探究、合作研究来证实一般性的结论(瓜豆原理)，并最终应用一般结论解决具体问题．在这样的探究活动中，学生经历了数学活动的全过程，从发现、证实到应用，不仅有问题解决更有问题提出，不仅有逻辑推理更有归纳猜想，不仅有教师点拨引导更有学生自主参与.这样的数学课堂因探究而精彩，因深度而富于启迪．

2.2 技术融合——探究活动的必然选择

“种瓜得瓜、种豆得豆”固然通俗易懂，但引用到数学问题中却显艰涩.我们应用GGB创设图3这样的活动场景，使所有学生都过目难忘，且“种瓜得瓜、种豆得豆”的想法或结论几乎都是瞬间脱口而出、异口同声．所谓“工欲善其事，必先利其器”，GGB不仅可对点进行变换操作，更可对曲线直接操作，如1.2第(2)步中我们增加指令“位似(旋转(f,α,P),t,P)”便可得到一新圆(与轨迹loc1重合)；也可从平面推广到三维空间；图11也只是增加一个指令输入而已.当然，对于本节课更有意义的是，我们可以将对于数学本质的考查寓于具体的操作之中(通过具体的操作强化对变换的认识)．事实上，数学有着高度概括的特性，在抽象的数学与生动的现实间构建联系通道，离不开现代教育技术的支持．我们需要借助技术的表征优势，为概念理解创设背景，为规律探索启发思路，为问题解决提供直观，真正促进学生的自主发现和真正理解，为学生“沉浸”于学习提供支撑．

图11