Extended Binding Number Results on Fractional(g,f,n,m) critical Deleted Graphs
Lan MeihuiGao Wei
(1.School of Information Engineering,Qujing Normal University,Qujing655011,China;2.School of Information Science and Technology,Yunnan Normal University,Kunming650500,China)
Abstract As an extension of the factor,the fractional factor allows each edge to give a real number in the range of0to1,and degree of fraction of each vertex to be controlled within a certain range(determined by the values of functions g and f,corresponding to the upper and lower fractional degree boundary).The score factor has a wide range of applications in communication networks,and the score critical deleted graph can be used to measure the feasibility of transmission when the network is damaged at a certain moment.In this short note,we mainly present some extended binding number conclusions on fractional(g,f,n,m) critical deleted graphs.
Key words Graph Binding number Fractional factor Fractional(g,f,n,m) critical deleted graph
1 Introduction
All graphs considered in this paper are simple and finite.LetGbe a graph with vertex setV(G)and edge setE(G).We denote bydG(v)andNG(v)(simply byd(v)andN(v))the degree and the neighborhood of any vertexvinG,respectively.Letδ(G)=minv∈V(G){d(v)}.ForS⊆V(G),we denote byG[S]the subgraph ofGinduced byS,and setG−S=G[V(G)S].For two vertex disjoint subsetsS,T⊂V(G),seteG(S,T)=|{e=uv|u∈S,v∈T}|.Notations and terminologies used but undefined in this paper can be found in[1].
Suppose thatgandfare two integer valued functions defined on vertex set ofGsatisfying0≤g(v)≤f(v)for anyv∈V(G).A fractional(g,f) factor can be considered as a functionhwhich assigns to each edge a number in[0,1]andg(v)≤(v)≤f(v)for each vertexv,whereh(e)is the fractional degree ofvinG.Ifg(v)=aandf(v)=bfor allv∈V(G),then a fractional(g,f) factor is a fractional[a,b] factor.A graphGis called a fractional(g,f,m) deleted graph if for each edge subsetH⊆E(G)with|H|=m,there exists a fractional(g,f) factorhsuch thath(e)=0for alle∈H.A graphGis a fractional(g,f,n,m) critical deleted graph if the resting subgraph after deletingnvertices fromGis a fractional(g,f,m) deleted graph.
We sayGhas all fractional(g,f) factors ifGhas a fractionalpfactor for eachp:V(G)→N withg(v)≤p(v)≤f(v)for anyv∈V(G).Ifg(v)=a,f(v)=bfor each vertexvandGhas all fractional(g,f) factors,then we say thatGhas all fractional[a,b] factors.A graphGis an all fractional(g,f,m) deleted graph if after deleting anymedge ofGthe remaining graph has an all fractional(g,f) factor.A graphGis an all fractional(g,f,n,m) critical deleted graph if after deleting anynvertices ofGthe remaining graph is an all fractional(g,f,m) deleted graph.Ifg(v)=a,f(v)=bfor eachv∈V(G),then an all fractional(g,f,n,m) critical deleted graph becomes an all fractional(a,b,n,m) critical deleted graph,i.e.,after deleting anynvertices ofGthe remaining graph is still an all fractional(a,b,m) deleted graph.




The following subsection depends heavily on two lemmas which are given by Liu and Zhang[1]and their equivalent description can be found in[3]and[4].We only prove Theorem1.1 since the tricks to prove Theorem1.2 and Theorem1.3 are the same.The main idea and tricks to prove Theorem1.1 are followed from[3]and[4],but we have new techniques here.
2 Proof of Theorem1.1
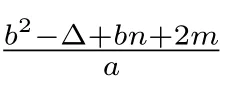

whereScontains at leastnvertices.
The subsetsSandTare chosen so that|T|is minimum.Clearly,T̸=∅anddG−S(x)≤b−1for anyx∈T.
The definitions ofl,H′,T0,H,H1,andH2are the same as in[3]and[4].If|V(H)|=0,then from(2.1)we obtain
a|S|≤b|T0|+bl+bn+2m−1
or


which contradicts todG−S(x)≤b−1for anyx∈T.We acquire

a contradiction by|T0|+l≥2.Therefore,we have|V(H)|>0.
Assume thatI1,C1,I(i)for1≤i≤binH1,andI2,C2,Tj,cj,ijfor1≤j≤b−1inH2(as well asWandU)are as the same as defined in[3]and[4].By Lemma3.5 in[4],we get

According to Lemma3.4 in[4],we infer

By the definition ofU,we acquire

LetX=T0∪lKb∪I1∪I2.Then,

wheret0=|T0|.Setbind(G)=B,then we get

By(2.4 ) (2.6 ),we infer

Using

and combining with(2.7),we get

In light of(2.3 ),(2.8 )and(2.2 ),we acquire

We consider two cases oft0+l.
Case1t0+l≥1.In this case,byaB≥b2+bn+m−∆,we haveaB(t0+lb)−b(t0+l)−bn−2m+1≥0.Thus(2.9)becomes

(b−2)(b−j)≥aB−aj−b+j.

Now consider

A contradiction can be obtained by using the similar discussion in[3]and[4].Therefore,whatever|I1|=0,or|I2|=0,or both|I1|≥1and|I2|≥1,we get a contradiction.
Case2t0+l=0.In this case,by(2.9)we acquire

The following discussion is divided into three subcases relying on whetherI1orI2is empty.
Subcase2.1|I1|=0.

We notice that(2.11)becomes Ifa=b,then(b−2)(b−j)−(aB−aj−b+j)≤j−a−bn−2m.Whenj=a−1,it reaches the minimum value−bn−2m−1,and whenj=a−2,it reaches the second minimum value−bn−2m−2.By learning the proof of Lemma2.3 in[1],we know that when choose the maximum independent set,for each connected component,we first select vertex which has minimum degree inG−S.ThusI2contains vertex which has degree at mostb−2inG−S,and furthermore we have(b−2)(b−j)−(aB−aj−b+j)≤j−a−bn−2m≤−bn−2m−2.Ifb≥a+1,then(b−2)(b−j)−(aB−aj−b+j)≤−bn−2m−2 since(a,b)̸=(1,2).In all,we get a contradiction to(2.12).
Subcase2.2|I2|=0.

It equals to

which contradicts to|I1|≥1.

Using the similar trick as in Subcase2.2,we deduce a confliction.
In all,the desired conclusion is completely proved.
3 Conclusion and discussion
In this contribution,we extended the result published in“Journal of Ambient Intelligence and Humanized Computing”by Gao et al.[5].Here,we introduce the following open problem.
Problem3.1What is the tight binding number bound(without parameter|V(G)|)for a graph to be fractional(g,f,n,m) critical deleted(resp.fractional(a,b,n,m) critical deleted or all fractional(g,f,n,m) critical deleted)?
- 数学理论与应用的其它文章
- Peakon,Pseudo Peakon,Periodic Peakon and Compacton Determined by Exact Solutions of Singular Nonlinear Traveling Wave Systems
- On the Geodesic transitivity of Finite Graphs
- Higher Accuracy Shape-preserving Modeling Based on the Two-level Fitting Method
- A Note on the Minimal Nonnegative Solution for Regular M matrix Algebraic Riccati Equations
- p2维融合范畴的扩张及应用
- 射影平面上点的合冲

