解一类变分不等式问题的半内点同伦方法

何 非, 商玉凤, 吴 睿

(1. 长春财经学院 数学教研部, 长春 130122； 2. 长春财经学院 经济学院, 长春 130122)

0 引 言

解有限维变分不等式问题(VI(X,F))就是找到一个向量x*∈X, 使得

(x-x*)TF(x*)≥0, ∀x∈X,

(1)

其中F是从n中的一个闭凸集X到n的一个映射, 称X为可行集.

变分不等式问题(VIP)在经济学、 交通运输、 区域科学等领域应用关泛, 目前求解变分不等式问题的算法主要有牛顿型方法、 投影型方法、 半光滑牛顿法和光滑化牛顿法.这些算法一般都是局部收敛的, 而具有全局收敛性的结果都建立在单调性假设或类似的条件下[1-3].同伦算法在求解非凸规划问题、 变分不等式问题中得到了许多有效结果[4-12].利用同伦算法解变分不等式问题不需要单调性假设.文献[5]给出了用动约束同伦算法求解变分不等式问题, 构造了一个满足X(t)⊆X(1)的动约束集X(t), 在较弱条件下证明了同伦路径的存在性, 初始点是X(1)的内点, 不需要为X的内点, 但不能保证解点x*∈X.

基于此, 本文给出一种新的同伦方程构造方法, 同样不需要初始点为X的内点, 但能保证解点x*∈X, 因此该方法使用更方便.数值算例结果表明了本文方法的有效性.

1 预备知识

本文假设可行集X为

X={x∈n:g(x)≤0,h(x)=0},

(2)

其中g(x):n→m,h(x):n→l.记X0={x∈n:g(x)<0,h(x)=0}, 称为严格可行集;I(x)={i|gi(x)=0,i∈{1,2,…,m}}, 称为紧指标集.

引理1[13]设gi(x)(i=1,2,…,m)是二次连续可微的凸函数,hj(x)(j=1,2,…,l)为线性函数,X由式(2)定义, 则x*是VI(X,F)的一个解当且仅当存在向量y*,z*, 使得(x*,y*,z*)是VI(X,F)的KKT系统:

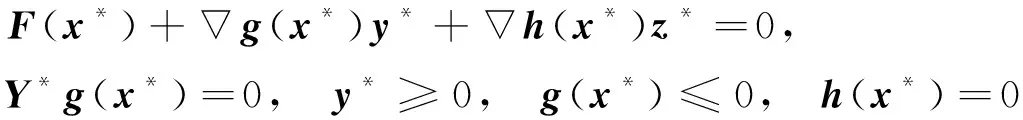
(3)

的解, 其中Y*=diag(y*).

为解系统(3), 构造半内点法组合同伦映射为

(4)

其中:

z∈l;w=(x,y)T,w(0)=(x(0),y(0))T;α(x(0),t)=(α1(x(0),1),…,αm(x(0),1))T,

式中δ∈(0,1).

记

X(t)={x∈n:gi(x)-αi(x(0),t)≤0,i=1,2,…,m},

X0(t)={x∈n:gi(x)-αi(x(0),t)<0,i=1,2,…,m},

∂X(t)=X(t)-X0(t),

I(x,t)={i∈{1,2,…,m}:gi(x)-αi(x(0),t)=0}.

假设条件:

(H1) Slater条件成立, 即X内部非空;

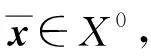
(5)

(H3) {gi(x),hj(x)|i∈I(x),j=1,2,…,l}正独立, 即对任给的和z∈l, 有

2 同伦路径的存在性及收敛定理

下面证明当假设条件(H1)～(H3)成立时,H-1(0)包含一条经过点(w(0),z(0),1)的有界光滑曲线, 当t→0时, 曲线另一端极限点(w*,z*,0)的x分量为VI(X,F)的解.

定理1设F:n→n,F∈Cp-1,gi∈Cp(p>2)(i=1,2,…,m), 且gi(x)为凸函数,h(x)为线性函数.假设条件(H1)～(H3)成立, 同伦映射H(w,z,t)由式(4)定义.则对几乎所有的非空并包含一条从(w(0),z(0),1)出发的光滑曲线Γ.如果(w*,z*,0)是曲线Γ在t=0的极限点, 则x*为式(1)的解.

其中

P=(P1,…,Pm)T,

G(x(0))=diag(g(x(0))-α(x(0),t)).

由α(x(0),t)的定义, 有g(x(0))-α(x(0),t)<0(i=1,2,…,m), 因此

于是DH(w(0),w,z,t)是行满秩的, 即0是H(w(0),w,z,t)的正则值.由参数化Sard定理和逆映射定理知, 对几乎所有的x(0)∈n和是H(w,z,t)的正则值且H-1(0)由一些光滑曲线组成.又由H(w(0),z(0),1)=0知, 必存在一条从(w(0),z(0),1)出发的光滑曲线, 记该曲线为Γ.取Γ上任一点列并记(w*,z*,t*)为当k→+∞时点列的极限点, 则可能发生下列几种情形:

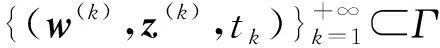
(1-tk)(F(x(k))+g(x(k))y(k)+h(x(k))z(k))+tk(x(k)-x(0))=0,

(6)

Y(k)(g(x(k))-α(x(0),tk))-tkY(0)(g(x(0))-α(x(0),1))=0,

(7)

h(x(k))-tkz(k)=0,

(8)

由方程(7)可知, 情形(iii)也不可能发生. 下证情形(i)也不可能发生.

由g(x(k))为凸函数, 有

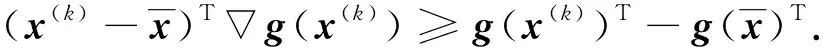
(10)

对式(10)两端右乘y(k), 并利用式(7), 有

(11)

于是

(12)

又因为

(13)

其次, 分下列3种情形说明‖(y(k),z(k))‖是有限的.

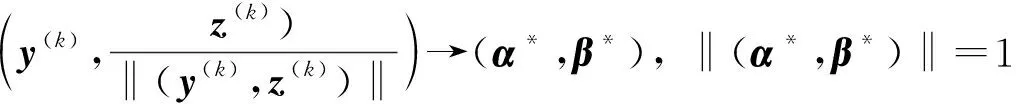
h(x*)α*+g(x*)β*=0,

(15)

与条件(H3)矛盾, 因此‖(y*,z*)‖是有限值.

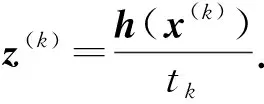
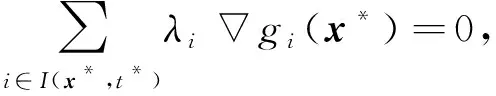
(16)

与g为凸函数矛盾, 因此‖y*‖是有限值.

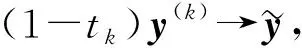
与g为凸函数矛盾, 因此‖y(k)‖是有限的.

综上所述, 只有情形(iv)成立, 因此当k→∞时, 极限点(x*,y*,z*)是系统(3)的解.

下面给出求解变分不等式问题的算例.

例1

例2

例3

表1 非内点法的计算结果

表2 半内点法的计算结果