带工作休假和工作故障的M/M/1/N排队系统性能分析

杨喜娟 ，李忠学，王海涌，武 福

(1.兰州交通大学电子与信息工程学院，甘肃 兰州 730070;2.兰州交通大学机电工程学院，甘肃兰州 730070)

1 引言

2002年，Servi和Finn[1]在M/M/1排队系统中引入了工作休假策略(working vacation，WV)，即服务台在休假期间不是完全停止工作，而是以较低的服务速率继续服务顾客.之后，工作休假策略在连续时间排队模型和离散时间排队系统中都得到了广泛研究.Liu和Xu等[2]在文献[1]的基础上，求解了M/M/1工作休假排队模型中稳态队长和等待时间的随机分解结构，并与经典M/G/1休假排队模型进行比较.Tian等[3]提出了拟生灭过程和矩阵几何解方法对M/M/1工作休假排队模型进行求解，得到系统稳态下顾客数的概率分布，并得到各项性能指标的随机分解.Li和Cheng[4]则分析了带有m-策略和(N，m)策略两种阈值策略的M/M/1工作休假排队模型，并应用拟生灭过程和矩阵几何解方法得到顾客数的分布和系统稳态概率等多项性能指标.Li等[5]和Tian等[6]讨论了考虑休假中断的M/M/1工作休假排队模型的顾客均衡加入策略和优化策略.张雪梅和岳德权等[7]对带有不耐烦顾客可批量到达的MX/M/1工作休假排队模型进行分析，使用概率母函数方法得到系统平均队长及稳态下系统顾客逗留时间等多项系统性能指标.张宏波和王红蔚[8]对正规忙期和工作休假期服务的顾客数服从不同分布的M/M/1排队模型进行分析，使用GI/M/1型Markov过程对系统进行建模分析，求解出系统稳态分布及队长的随机分解结构.Wu和Takagi[9]将工作休假策略拓展到服务时间为一般分布的M/G/1休假排队模型，通过瞬态解分析，求解出了系统队长的稳态概率分析和任意顾客系统逗留时间的拉氏变换.Baba[10]考虑了到达过程为一般分布的GI/M/1工作休假模型，求解得到了到达时刻和任意时刻顾客数的稳态分布及任意顾客的逗留时间.在文献[10]的基础上，Kempa和Martyna[11]则利用线性代数方法分析了带有限缓存的GI/M/1工作休假模型中瞬时队长分布.相应地，Tian等[12]将工作休假策略拓展到离散时间排队模型Geom/Geom/1中，使用拟生灭过程和矩阵几何解方法得到系统队长和顾客等待时间的分布.Li[13]应用M/G/1经典休假模型矩阵分析方法对离散时间Geo/G/1工作休假排队模型进行分析，得到系统稳态队长的概率分布函数.Yu等[14]研究分析了带有启动时间和有限缓存的GI/Geom/1工作休假排队模型，应用离散Markov链和补充变量法求得不同时刻稳态队长的分布及其顾客逗留时间的概率质量函数等多项系统性能指标.

上述文献考虑的工作休假排队模型，都是假定服务台不会出现故障的，但在实际中经常会碰到服务台发生故障，修理后继续为顾客服务的情形.而现有文献中考虑服务台故障工作休假排队模型的相对较少.Jain等[15]研究了服务台可有多重故障的M/M/1工作休假模型，利用矩阵几何方法求得了稳态队长等系统性能指标，同时，利用母函数法对服务时间服从埃尔朗分布的M/Ek/1工作休假模型进行分析，求得稳态队长等性能指标，并对系统性能的敏感性进行分析.Rajadurai 等[16]在带有可修服务台和反馈重试策略的M/G/1休假排队模型中考虑了工作休假策略，并使用补充变量法求得了稳态队长的概率分布函数.Ma等[17]研究了带有启动时间、伪故障和N-策略的离散时间Geo/Geo/1工作休假排队模型，并通过拟生灭过程和矩阵几何解方法求解得到系统稳态队长的分布和各项系统稳态性能指标.最近，黎锁平等[18]研究了带启动时间和可修服务台的M/M/1/N工作休假排队模型，使用拟生灭过程和矩阵几何方法得到系统方差、系统稳态可用度、系统吞吐率、系统队长等多项性能指标，并对系统的敏感性进行分析.

2012年，Kalidass和Kasturi[19]将工作故障策略引入了M/M/1可修排队系统.与工作休假策略相同的是，服务台有可变服务速率的能力，不同的是，服务台在故障期可低速为顾客服务.文献[19]使用概率母函数求得稳态下服务台状态和队长的联合分布、顾客等待时间分布及多项系统性能指标.Yang和Wu[20]在带有限缓存和不耐烦顾客的M/M/1排队模型中考虑了工作故障策略，采用四阶龙格-库塔方法得到系统的瞬态特点，并用矩阵方法对系统的稳态概率进行求解.Ma和Cui[21]研究了带多重休假、到达率可变和工作故障策略的M/M/1排队模型，使用拟生灭过程和矩阵几何解方法得到稳态队长的分布及期望，并对系统性质进行分析.杨喜娟等[22]对带有启动时间、有限缓存和工作故障的M/M/1/N排队模型进行分析，使用拟生灭过程和矩阵几何方法得到系统吞吐率、系统稳态可用度及多项稳态性能指标，并对系统的敏感性进行分析.Zhang和Gao[23]对有备用服务台和因工作故障导致不耐烦顾客的M/M/1模型进行分析，求解得到队长的分布及其队长和指定顾客逗留时间的均值.马占友等[24]在带不耐烦顾客的多重休假M/M/1排队模型中引入了工作故障策略，使用母函数法求解得到不同状态下队长的概率母函数，并求解出稳态队长等系统性能指标.同时，许多学者将工作故障策略拓展到其他排队模型中.Kim和Lee[25]对带有备用服务台的M/G/1排队模型中引入了工作故障策略，计算求得队长和顾客逗留时间的分布，分析得到系统参数对逗留时间影响情况.Li和Zhang[26]在重试时间为一般分布的M/G/1重试排队模型中考虑了工作故障策略，使用补充变量法，得到队长的一般分布及各项稳态概率.Rajadurai[27]考虑了带工作休假和工作故障策略的重试M/G/1排队模型，使用补充变量法得到系统稳态队长的概率母函数及多项系统稳态性能指标.Liu和Song[28]在批量到达的MX/M/1排队模型中考虑了工作故障策略，建立系统的二维Markov链模型，求得稳态队长的概率母函数及其随机分解结构.Li等[29]对有负顾客和工作故障的MX/G/1模型进行分析，使用补充变量法和矩阵分析方法得到队长的概率母函数及多项系统性能指标.Jiang和Liu[30]对一般到达过程和多阶段服务的GI/M/1排队模型中考虑了工作故障策略，使用矩阵分析方法和semi-Markov过程，得到顾客到达时刻、任意时刻稳态队长的分布和顾客逗留时间的分布.Ye和Liu[31]对考虑工作故障和到达过程服从Markov过程的MAP/M/1 排队模型进行分析，使用矩阵几何方法得到系统稳态队长、稳态顾客逗留时间的递归公式等系统性能指标.Jain等[32]考虑了机器在维修过程中带工作故障和维修工在休假过程中带工作休假策略的容错加工系统，使用矩阵方法得到瞬时队长分布及多项稳态性能指标.Gao等[33]使用嵌入Markov链和补充变量法，求得带工作故障策略的离散时间排队模型中顾客离开时刻队长的分布及任意时刻队长和机器状态的联合分布等.

综合现有考虑工作休假或工作故障策略的排队模型的文献，同时考虑了启动时间和有限缓存的文献相对很少，且仅文献[27]同时考虑了工作休假和工作故障策略.本文受文献[27]的启发，在文献[18，22]的基础上，在带启动时间和有限缓存的M/M/1/N排队模型中，同时引入工作休假和工作故障策略，并考虑了机器在不同的服务阶段都可能出现故障，以填实这方面研究的内容.实际应用中经常会有这种情况出现.比如，在生产制造系统中，企业会通过尽量减少停机次数来提高生产效率，当系统中没有可生产的产品时，机器将不立刻停机而是进入工作休假期，在此期间，若有需要加工的产品，机器仍可以较低速度进行生产，直至工作休假结束进入正常生产;当机器出现故障时，可不停机修理或使用备用机器直到机器修理完成进入正常生产.由于启动时间、工作休假和工作故障等策略，以及不同阶段机器故障的引入，增加了问题求解的难度，仅使用经典排队理论难于对系统进行建模.本文的主要贡献是建立了带有启动时间、同时考虑工作休假和工作故障策略的M/M/1/N排队模型的拟生灭过程模型，且除了求得系统吞吐率、系统稳态队长及各项稳态状态概率等性能指标外，还使用基本阵和协方差矩阵理论知识求得了系统方差和系统稳态可用度.这一研究是现有关于带工作休假和工作故障策略排队系统的文献中从未涉及的，但将为此类排队模型的实际应用提供很好的理论依据.本文解决的主要问题是:1)建立带有启动时间、工作休假和工作故障的M/M/1/N排队模型的三维时间Markov过程;2)通过分析系统平衡方程，得到系统有限状态拟生灭过程;3)使用矩阵几何解方法求解出系统稳态概率向量，在此基础上求解系统方差、稳态可用度、系统吞吐率及其各稳态状态概率等多项性能指标，并通过数值实验对系统敏感性进行分析.

本文的结构安排如下:第2节描述系统模型;第3节建立系统的连续时间三维Markov模型，分析得到系统平稳方程，将模型表示为有限状态拟生灭过程，通过矩阵几何方法求解系统稳态概率向量;第4节对机器各种状态的参数进行限定，给出几种典型情况;第5节在系统稳态概率向量的基础上，求解系统方差、系统稳态可用度、系统吞吐率及其他各项稳态概率等系统性能指标;第6节通过数值实验，分析系统性能指标的敏感性;第7节为结论.

2 模型描述

考虑一个带有启动时间、工作休假和工作故障的可修M/M/1/N排队系统，其模型描述如下:

1) 缓冲区:到达服务系统的顾客依次进入缓冲区，缓冲区的容量为N(不包括正在服务的顾客);

2) 服务规则:服务台遵循先来先服务的服务策略，且一次只能为一个顾客服务;

3) 到达过程:顾客的到达过程是参数为λ的Poisson过程，当缓冲区为满时，到达的顾客将不能进入系统;

4) 正规服务过程:在正规忙期，服务台的服务速率服从参数为μ的指数分布;

5) 工作休假过程:在工作休假期，服务台以较低的服务速率为顾客服务，且服务速率服从参数为μw(μw＜μ)的指数分布;

6) 休假过程:当系统中无顾客时，服务台进入一个随机长度为V、服从参数为θ的指数分布的休假，即平均休假时间为.在休假期内，如果系统有顾客到达，则服务台进入工作休假期;当休假结束时，如果缓冲区中有顾客，则服务台进入正规忙期.否则，服务台进入一个关闭期;

7) 启动过程:在关闭期内，如果系统中有顾客到达，则结束关闭期进入启动期，启动时间服从参数为s的指数分布，即平均启动时间为.启动期结束后，系统进入正规忙期;

8) 故障过程:服务台在运行过程中随时会出现故障，且在关闭期、启动期、休假期和正规忙期的服务台的寿命时间分别服从参数为α，αs，αw和αb的指数分布，即平均寿命时间分别为修理时间分别服从参数为β，βs，βw和βb的指数分布，即平均修理时间分别为.服务台出现故障后立即进行修理，且在正规忙期，服务台并不是完全停止工作，而是以较低的服务速率为顾客服务，且服务速率服从参数为μb(μb＜μ)的指数分布.当维修完成后，若系统中有顾客，服务台的服务速率重新调整为μ继续为顾客服务，否则，系统进入休假期;

9) 假设系统中的各种随机变量之间相互独立.

从模型的描述来看，在该模型中，具有3个服务速率μ，μw，μb(μw＜μ，μb＜μ)，当系统处于工作休假期和工作故障期时，服务台分别以慢速率μw，μb为顾客服务，当系统处于正规忙期时，服务台以服务速率μ为顾客服务，可见该模型本质上属于具有可变服务速率的可修排队系统，仍可使用Markov过程的理论知识对模型进行求解.

3 稳态概率向量求解

3.1 系统平稳方程

令L(t)为t时刻系统中的顾客数，则0≤L(t)≤N，C(t)为t时刻服务台的工作状态，且

设W(t)表示t时刻服务台是否有故障，且

则{L(t)，C(t)，W(t)}为三维Markov 过程，其状态空间为

其中:(0，1，0)表示系统处于关闭期，且服务器出现故障;(0，1，1)表示系统处于关闭期，且服务器无故障;(k，1，1)，k≥1表示系统处于启动期、缓冲区中有k个顾客且服务器无故障;(k，1，0)，k≥1表示系统处于启动期、缓冲区中有k个顾客且服务器有故障;(k，2，1)，k≥0表示系统处于休假期、缓冲区中有k个顾客且服务器无故障;(k，2，0)，k≥0 表示系统处于休假期、缓冲区中有k个顾客且服务器有故障;(k，3，1)，k≥1表示系统处于正规忙期、缓冲区中有k个顾客且服务器无故障;(k，3，0)，k≥1表示系统处于正规忙期、缓冲区中有k个顾客且服务器有故障.系统的状态转移图如图1所示.

图1 带工作休假和工作故障的M/M/1/N排队系统状态转移图Fig.1 State transition diagram of M/M/1/N queueing system with working vacation and working breakdown

根据图1且系统在稳态下给定状态的转移出入率平衡，可得系统的平稳方程为

为了计算的方便，将状态k=0用状态k=1进行表示.在 式(1)-(3)中，将P(0，1，0)，P(0，1，1)，P(0，2，0)用P(0，2，1)表示，有

对状态按字典序排列，可得到系统的无穷小生成元为

即Q为分块三对角矩阵，则根据文献[34-35]可知，Markov过程{L(t)，C(t)，W(t)}为有限状态的拟生灭过程(quasi birth and death，QBD)，为后续计算方便起见，记Q=(qij)，i，j=1，2，3，···，6×N.

3.2 求解稳态概率向量

鉴于分块矩阵C=λI(I为6阶单位矩阵)为对角阵，结合文献[36]的矩阵几何方法，对Q的稳态概率向量进行求解.设Q的系统稳态概率向量为π=(π1，···，πN)，其中子向量πi(1 ≤i≤N)为6 维行向量.求解平衡方程πQ=0和归一化方程πe=1(e是值为1的列向量)，结合式(15)，得到以下矩阵形式的方程组:

且由归一化条件

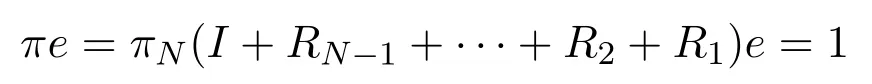
可求得πN，即而稳态概率向量π得以求解.

4 典型情况

对系统中的某些参数作特殊限定后，当前系统将被简化.本部分对简化后的模型做一简要分析.

1) 服务台无故障.

这种情况下，系统中服务台无故障，即服务台的平均寿命时间趋于无穷大，服务台的平均修理时间趋于无穷小，同时，无故障期服务速率，对应参数取值为μb=0，

此时，本系统简化为带有启动时间的M/M/1/N单重工作休假排队模型，由于服务台没有故障，系统中的状态可用二维Markov状态表示，系统的状态转移图如图2所示.系统求解过程和系统性能的求解可参考文献[37].

2) 空闲期和启动期无故障，无工作故障.

这种情况下，系统参数为μb=0，

此时，本系统简化为带有启动时间和可修机器的M/M/1/N工作休假排队模型，系统状态转移图、系统建模和系统性能的求解过程可参考文献[18].

3) 空闲期和启动期无故障，无工作休假.

这种情况下，空闲期和启动期无故障，即空闲期和启动期服务台的平均寿命时间趋于无穷大，空闲期和启动期服务台的平均修理时间趋于无穷小，系统参数为μw=0，

此时，本系统简化为带有启动时间和工作故障的M/M/1/N排队模型，系统状态转移图、系统建模和系统性能的求解过程可参考文献[22].

4) 服务台无故障，不考虑工作休假策略.

这种情况下，系统中服务台无故障，同时，对应故障期和休假期均无服务速率，则参数取值为μb=0，μw=0，

此时，本系统简化为带有启动时间的M/M/1/N休假排队模型，由于服务台没有故障，系统中的状态可用二维Markov状态表示，系统的状态转移图如图3所示.

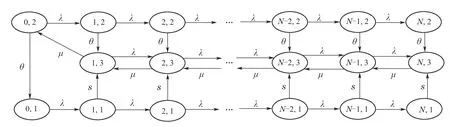
图3 带启动时间的M/M/1/N排队系统状态转移图Fig.3 State transition diagram of M/M/1/N queueing system with setup time

5) 无启动时间，空闲期无故障.

这种情况下，系统中无启动时间，即平均启动时间趋于0，即s →∞，空闲期服务台无故障，即空闲期服务台的平均寿命时间趋于无穷大，服务台的平均修理时间趋于无穷小，即α →0，β →∞，本系统简化为无启动时间、带工作故障和工作休假的M/M/1/N排队模型，系统的状态转移图如图4所示.

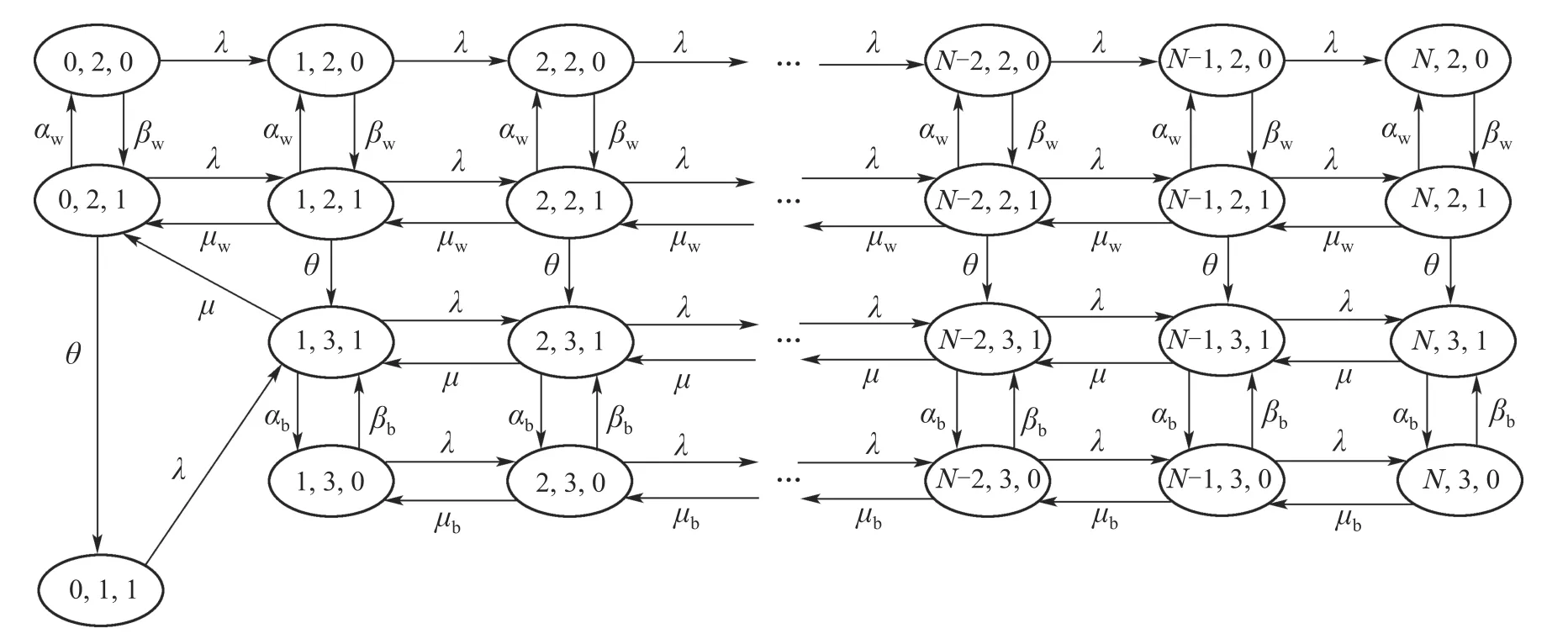
图4 无启动时间、带工作休假和工作故障的M/M/1/N排队系统状态转移图Fig.4 State transition diagram of M/M/1/N queueing system with working vacation and working breakdown and no setup time

对于情况4)-5)，当前文献中还没有具体的求解过程，这部分内容将在后续的研究中进行求解，本文中不给出具体求解过程.

5 系统性能指标

5.1 系统稳态概率

根据平稳方程及其第3.2节中求解出的稳态概率向量π的值，可计算出系统稳态概率如下.

1) 系统处于关闭期的概率.由式(12)有

2) 系统处于正规忙期的概率

3) 系统处于无故障启动期的概率

4) 系统处于无故障工作休假期概率

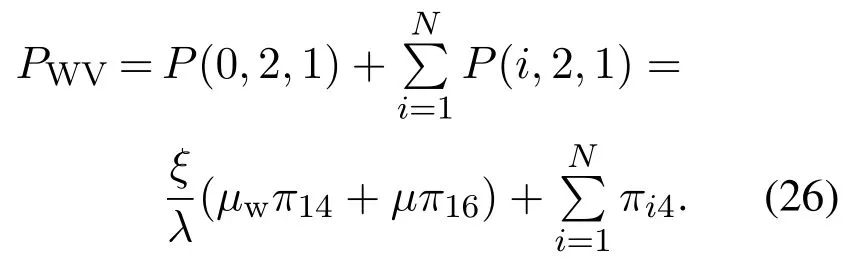
5) 系统处于故障期的概率

5.2 系统稳态性能

根据系统稳态概率向量和系统各稳态概率，可求得以下稳态性能.

1) 系统稳态可用度和系统方差.

设σi(n)表示从某一初始状态出发，n个服务周期中系统仍处于状态i的次数;cov(σi(n)，σj(n))表示从某一初始状态出发，n个服务周期中系统处于状态i的次数和系统处于状态j的次数的协方差，记为cij;

为第3.2节中所求的平稳概率向量.

设系统的概率转移矩阵为P，根据参考文献[38]和文献[39]，此QBD过程的基本阵表示为

其中I为单位阵，e为元素都是1的(6×N)维列向量.而P=I -Y Q，其中

则可得到此QBD过程的基本阵为F=(Y Q+eπ)-1.

由此，系统的协方差矩阵C={cij}由下式确定:

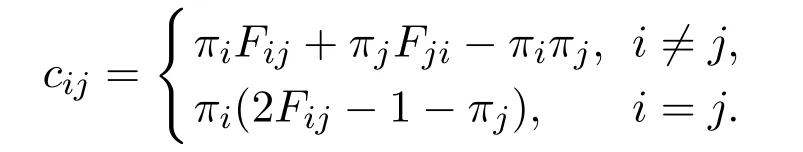
设U为服务台处于工作故障状态、工作休假期或正常忙期的有效状态集，即

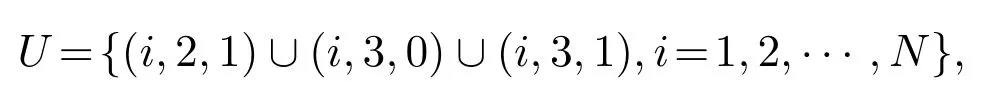
则系统的稳态可用度和系统方差为

2) 系统吞吐率

3) 系统稳态队长

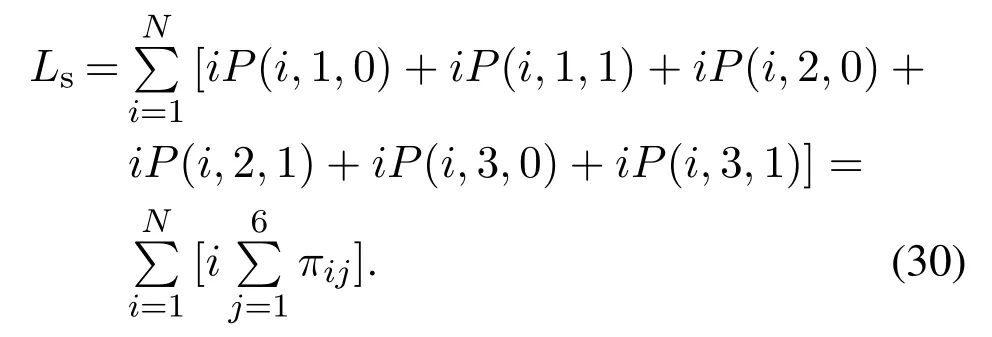
6 数值分析

本节在MATLAB R2016a平台下进行一些数值实验，给出各系统参数对系统性能的影响情况.

在稳态条件下，设定缓冲区容量N=8，基本参数λ=4，μ=5，μw=4，μb=2，θ=5，s=4，α=0.2，β=5，αs=0.3，βs=4，αw=0.4，βw=5，αb=0.5，βb=5.在保证μw＜μ，μb＜μ和矩阵B1可逆的前提下，改变各参数取值，分析各参数对系统性能的影响.图5-11给出了参数α，αs，αw，αb，β，βs，βw，βb，μ，μw，μb，λ，θ，s，N变化时对系统性能的影响情况.

图5 服务台的寿命时间参数对系统性能的影响Fig.5 Influence of parameters of the server’s life time to system performances

从图5中可看出:1)TP，PB，PI，PS，PWV均会随着α，αs，αw，αb的增大而减小;2)Ls，PF均会随着α，αs，αw，αb的增大而增大;3)Avai随着α，αs，αw的增大而减小，而随着αb的增大而增大;4)α和αs对V几乎没有影响，而V随着αw的增大而增大，随着αb的增大，V有先增后减，之后趋近于0的变化过程.

从图6(a)中可以看出，β对系统各性能指标的影响都特别小，而从图6(b)-6(d)可以看出，当βs，βw和βb取值较小时，各系统性能指标的变化趋势较为明显，而当βs，βw，βb增大到一定值后，各系统性能指标的变化趋于平缓.具体地，1)TP，Avai，PB，PI，PS，PWV随着βs，βw的增大而增大，Ls，PF和V随着βs，βw的增大而减小，2)随着βb的增大，TP，PB，PI，PS，PWV，Ls，PF与上述有相同的变化趋势，而Avai有减小的趋势，V有增大的趋势.

图6 服务台的修理时间参数对系统性能的影响Fig.6 Influence of parameters of the server’s repair time to system performances

从图7(a)可以看出，相比较于μw和μb，μ对系统各性能指标的影响较大，且TP，PI，PS，PWV，PF随着μ的增大而增大，Ls，Avai，PB，V随着μ的增大而减小，且当μ增大到一定值后，V的取值趋近于0;而μw和μb仅对TP和Ls有较大的影响，且TP和Ls的变化曲线接近于线性变化.具体地，TP均随着μw和μb的增大而增大，Ls随着μw的增大而增大，随着μb的增大而减小;V随着μb的增大而增大.

图7 服务台的服务速率参数对系统性能的影响Fig.7 Influence of parameters of the server’s serving rate to system performances

从图8可以看出，λ对系统性能指标的影响较大，且对Ls和PI的影响最明显.具体地，TP，Avai，Ls，PB随着λ的增大而增大，PI，PF，PS，PWV，V随着λ的增大而减小，并且当λ增大到一定取值后，PI，PS，PWV，V的取值趋于0.

图8 系统到达过程参数λ对系统性能的影响Fig.8 Influence of parameters of the customers’ arriving rate λ to system performances

由图9可知，TP，Avai，Ls，PWV随着θ的增大而减小，PB，PI，PF，PS，V随着θ的增大而增大，且θ对PWV的影响最为明显.

图9 系统休假时间参数θ对系统性能的影响Fig.9 Influence of parameters of the server’s vacation time θ to system performances

而从图10可以看出，TP，Avai，PB，PI，PF，PWV均随着s的增大而增大，Ls，PS，V随着s的增大而减小，且对系统的各性能指标的影响均较大.由此可见，为了提高系统生产率，可增大s的取值，即减小系统平均启动时间.从图11中可以看出，TP，Avai，PB，Ls随着N的增大而增大，PI，PF，PWV，PS，V随着N的增大而减小.同时，当N增大到一定取值后，除Ls外，其余各性能指标几乎不再受N的影响.因此，在实际应用过程中，考虑到节约成本，缓存区的容量并不是设置的越大越好.

图10 系统启动时间参数s对系统性能的影响Fig.10 Influence of parameters of setup time s to system performances

图11 缓冲区容量N对系统性能的影响Fig.11 Influence of buffer capacities N to system performances

图12分析了在M/M/1/N休假模型、M/M/1/N工作休假模型、M/M/1/N工作故障模型及带工作休假和工作故障的M/M/1/N模型4种不同的排队系统中，μ对系统稳态可用度Avai和系统吞吐率TP的影响情况，其中在工作休假模型中μw仍表示工作休假期的服务速率，在工作故障模型、带工作休假和工作故障策略的模型中μb仍表示为工作故障期的服务速率.4种模型通用的参数为λ=5，μw=4.5，θ=1.5，s=1，α=3，β=4，N=5，且在工作休假和工作故障策略的模型中，其余参数的取值为μb=4.9，αw=0.5，βw=8，αs=0.5，βs=8，αb=2，βb=2.

由图12可见，在4种排队模型中Avai均随着μ的增大有减小的趋势，相比于M/M/1/N 休假模型、M/M/1/N 工作休假模型、M/M/1/N 工作故障模型，带工作休假和工作故障的M/M/1/N模型Avai随μ的变化较小，即带工作休假和工作故障的M/M/1/N模型的服务台稳态可用度较高，这与服务台利用休假期和故障期仍可为顾客服务有关.在M/M/1/N工作休假模型中，当μ较小时，TP随着μ的增大而增大，而当其值增大到一定值后，TP随着μ的增大有减小的趋势，而其他3种模型中TP均随着μ的增大而增大，且带工作休假和工作故障的M/M/1/N模型的增大趋势较M/M/1/N休假模型和M/M/1/N工作故障模型更为明显.

图12 4种排队系统中μ对TP和Avai的影响Fig.12 The influence of μ on TP and Avai in four different queueing systems

因此，带工作休假和工作故障的M/M/1/N模型一定程度上弥补了M/M/1/N工作休假模型和M/M/1/N工作故障模型中μ对TP的影响趋势.

综合上述分析，本文发现:

1) 空闲期服务台寿命时间和修理时间对各系统性能指标的影响最小，正规忙期服务台寿命时间和修理时间对各系统性能指标的影响最大.同时，随着平均寿命时间的增大(或平均修理时间的减小)，系统吞吐率有增大的趋势，而系统稳态队长和系统处于故障期的概率有减小的趋势.

2) 比较服务台各时期的服务速率，服务台在正规忙期的服务速率对各系统性能指标的影响最大.但就对系统吞吐率和系统方差的影响而言，系统吞吐率均随着服务台在正规忙期的服务速率、在工作休假期的服务速率、在工作故障期的服务速率的增大而增大;而随着正规忙期的服务速率的增大，系统方差有减小的趋势，随着工作故障期的服务速率的增大，系统方差有增大的趋势;而随着工作休假期的服务速率的增大，系统方差有增大的趋势，但变化浮动相对较小.理想的实际应用系统是系统吞吐率越大越好，而系统方差越小越好，因此，从这个角度出发，增大服务台正规忙期的服务速率是增加系统吞吐率，降低系统方差的最有效方式.

3) 随着平均启动时间的减小，系统吞吐率和系统稳态可用度均增大，而系统稳态队长和系统方差均会减小，因此为提高系统吞吐率，降低系统方差，需采取有效措施减少启动时间.

4) 系统中的缓存区容量并不是越大越好，当缓存区容量增大到一定值后，除稳态队长外各系统性能指标的变化均趋于平缓，取值均不再发生变化.因此，需要根据系统各参数取值选择合适的缓存区容量.

5) 同时引入工作休假和工作故障策略，此系统中工作休假时间对系统吞吐率影响的变化规律与文献[18，22]有所不同，系统吞吐率会随着平均工作休假时间的减小而减小;同时，在文献[18]，当正规忙期服务速率较小时，系统吞吐率会随之增大，而当正规忙期服务率较大时，系统吞吐率会有小幅的下降，之后趋于平缓.而在本文提出系统中，系统吞吐率随着正规忙期服务速率的增大而增大;数值分析表明，同时带有工作休假和工作故障策略的M/M/1/N排队系统的系统吞吐率高于仅带有工作故障策略的M/M/1/N排队系统，因此，同时引入工作休假和工作故障策略的M/M/1/N排队系统一定程度上可改善仅带工作休假策略或工作故障策略的M/M/1/N排队系统的系统性能.

7 结论

本文对带有启动时间、工作休假和工作故障策略的M/M/1/N排队系统进行了分析.在这种排队系统中，服务台在休假期和故障期仍以较低的服务速率为顾客服务，且服务台在启动期、休假期和正规忙期有不同的寿命时间和修理时间，这种情况比服务台无故障或仅在正规忙期有故障更贴近于实际.文中考虑的模型在当前竞争日趋激烈的制造业生产和维修过程中广泛存在.通过对此模型三维连续时间Markov链最小生成元的分块矩阵化表示，得到系统的有限状态拟生灭过程，并使用矩阵几何方法求解出系统稳态概率向量，从而给出系统稳态可用度、系统方差、稳态队长及各稳态概率等多项性能指标.本文中使用的拟生灭过程和矩阵几何方法将为研究复杂环境排队系统提供很好的理论依据，对作者更近一步的研究带有工作休假和工作故障策略M/M/1/N排队系统的定性研究有很大的启发性.在后续的研究工作中，将研究带有工作休假和工作故障策略的其他排队模型，并尝试拓展到多服务台系统或排队网络中，同时，将应用此模型求解制造业等实际复杂服务系统中的诸多问题，考虑各系统参数的组合优化，以期为实际应用提供理论依据.