热波耦合系统的指数镇定及其H∞鲁棒性
金雪莲,张思佳,郑 福
(1.辽宁工业大学 理学院,辽宁锦州 121002;2.渤海大学 数学科学学院,辽宁 锦州 121013)
1 引言
本文研究由如下偏微分方程组描绘的一维热波耦合系统,

这个系统是一维空间中流体结构交互作用的线性化模型,由一根热杆和一根振动的弦组成.这里假设热杆所占的空间为(-1,0),弹性弦所占的空间为(0,1),z(t,x)表示t时刻热杆在x ∈(-1,0)处的温度,y(t,x)表示t时刻震动弦在x ∈(0,1)处偏离平衡态的位移,热杆的左端点温度恒为零,在弦的右端实施Neumann边界控制yx(t,1)=u(t),并具有同位速度观测O(t)=yt(t,1),热杆和弦在内部节点x=0(也称作传输界面)相连.文献[1]对系统的零可控性、可观性和稳定性进行了详细的研究,结果表明当控制u(t)=0时,系统是多项式稳定的,而不是指数稳定的;当控制u(t)存在时,系统是零可控的.文献[2-3]给出了更多相关的结果,但是在系统的稳定性分析方面,只是得到系统是多项式稳定的,而不是指数稳定的.
系统(1)具有多项式稳定性的原因在于它是由一个指数稳定的系统(热方程部分)和一个能量守恒系统(波方程部分)耦合在一起的,由于连接2个部分的耗散机制太弱,只有热方程部分是指数稳定的,并不能把整个系统交互作用成指数稳定的.文献[4]的研究结果进一步表明,即使将控制u(t)设计为如下的动态反馈控制:

此时波方程部分相应于一个多项式稳定的系统(见文献[5]),但是整个系统仍然是多项式稳定的.可见想要指数镇定系统(1),需要从指数稳定的波方程中寻找控制,因而受文献[6-10]的启发,本文采用如下负比例反馈:

和动态反馈控制

其中:u(t)∈Rn是控制器的状态,A ∈Rn×n是常数矩阵,b,c ∈Rn是列向量,d是正常数.本文主要采用Lyapunov函数法验证系统(1)在负比例反馈控制(2)和动态反馈控制(3)-(4)下都是指数稳定的.
系统(1)描绘的是流体结构交互作用的线性化模型,原模型应该是由Navier-Stokes方程和弹性方程通过自由接触界面耦合在一起的,但是对于这种复杂的情形,系统解的存在性和唯一性都是未解决的难题,文献[12]给出了变形的此类系统的解的存在性相关结果.相比较而言,虽然系统(1)易于研究,但是它的稳定性分析不但是非平凡的,而且还是非常复杂和困难的.事实上,耦合方程一直是工程学、数学和控制论中的重要研究内容,特别是耦合方程的镇定是热点研究问题,但有一定困难和复杂性[13-17].除了上面提及的热波耦合系统[11]外,还有抽象双曲-抛物耦合系统(Russell将这种耦合称之为间接阻尼机制)[18-19]、波-波耦合系统[14,20-21]、热弹性系统[15,19,22-23]、流体结构通过界面耦合系统[24-26]、热-波平面网络系统[27]、梁方程-波方程耦合系统[16]和梁方程-薛定谔方程耦合系统[17]等.
负比例反馈(2)是非常经典的,可见文献[10,28]及其中的参考文献.动态反馈控制(3-4)来自[6-9].但是事实上,动态反馈控制在当代控制论中是广泛使用的[29-32],特别是输出调节问题中的鲁棒控制仅在动态控制中是存在的,这可由内模原理得到[33](Lemma 1.21,p.19).关于无穷维空间上抽象系统的动态控制和静态控制之间的关系可见文献[34-35].
本文结构如下:第2节对相应于负比例反馈(2)的闭环系统的指数稳定性进行了研究;第3节对相应于动态边界反馈(3)-(4)的闭环系统的指数稳定性进行了研究;第4节给出了2种控制是H∞鲁棒的充分条件;第5节是总结和展望部分.
2 静态反馈系统的指数稳定性
系统(1)在静态反馈(2)下的闭环系统为
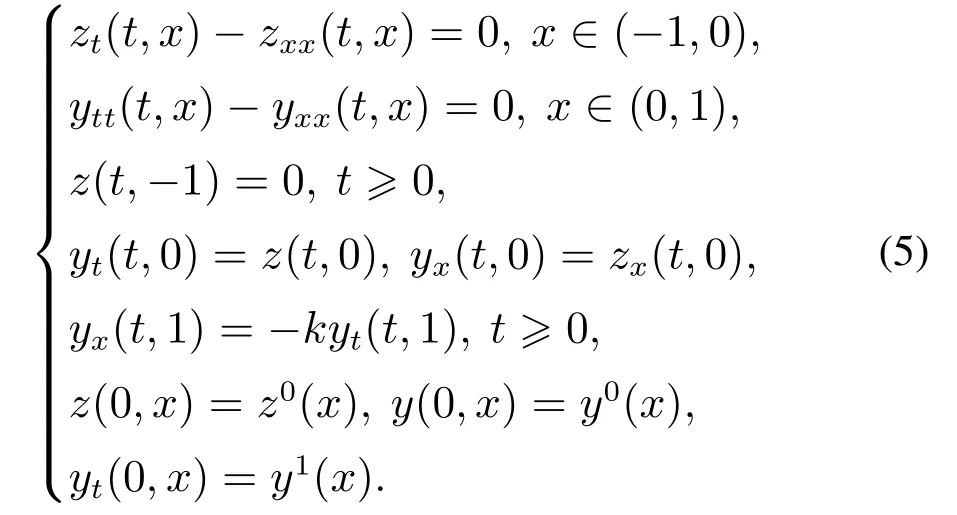
引入系统(5)的状态空间为

及其内积

是相应于上述内积导出的范数.
若令X(t)=(z(t,-x)y(t,x)yt(t,x))T,则可将系统(5)写成抽象微分方程形式:

定理1算子B在H上生成的半群是收缩的C0半群.
证很容易看出,算子B是稠定闭算子,由直接计算得

进而有Re〈Bm,m〉≤0,即B是耗散算子.此外,利用共轭算子的定义,易于求得

所以,B*也是耗散算子,进而得出由算子B生成的半群T(t)是收缩半群[36](定理6.1.8). 证毕.
利用算子半群理论可知系统(5)是适定的,并且系统(5)的唯一解可以由T(t)X0给出.此外,从定理1的证明和能量E(t)与半群T(t)的关系可知系统(5)能量满足

为了得到系统(5)的指数稳定性,令0<ε <1是可以自由选取的参数,构造Lyapunov函数:G(t)=E(t)+εφ(t),其中φ(t)是待定的函数.为了给出εφ(t)的具体表达式,首先由式(5)的第1个等式并利用分部积分公式有


而且根据能量E(t)和Lyapunov函数G(t)的表达式,还有如下性质.
引理1Lyapunov函数G(t)等价于能量E(t),即如下关系式成立:
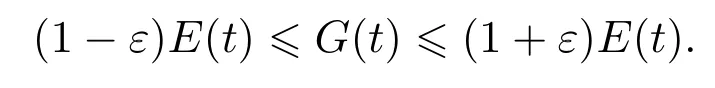
引理2辅助函数φ(t)满足
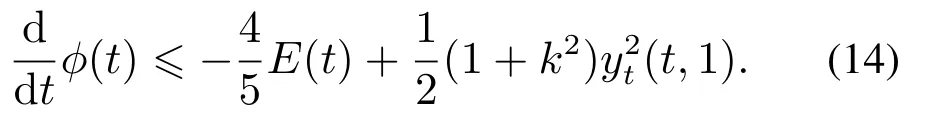
在给出本节的主要结果之前,先给出一个注.
注1辅助函数φ(t)由3部分组成,前2部分分别来自研究热方程和波动方程指数稳定性所用到的Lyapunov函数[37],第3部分是为了消掉交叉项yt(t,0)yx(t,0)而引入的.辅助函数的系数是为了平衡φ(t)中各项使其相关项合在一起与能量E(t)中各项一致,可见,系数的选取是不唯一的,也就是说辅助函数φ(t)有无穷多种设计方法.
定理2能量E(t)具有如下指数衰减率:
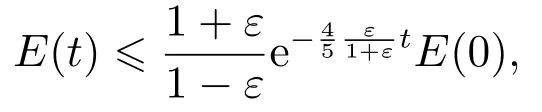
其中ε满足0<ε <1.
证由式(8)和引理2可知
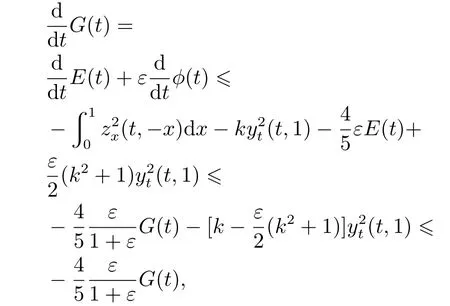
其中:选取参数ε确保

最后由引理1得

3 动态反馈系统的指数稳定性
系统(1)在动态反馈控制(3)-(4)下的闭环系统为

其中A,b,c,d和w(t)在引言中已给出.本节的结果依赖于如下假设:
H1:矩阵A的所有特征值有负实部;
H2:(A,b)是可控的和(c,A)是可观的;
H3:对任意的实数s,存在另一常数γ≥0,使得d≥γ和
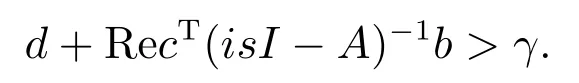
由Meyer-Kalman-Yakubovich引理[6](P.1786)可知,在这几个假设下,对给定任意对称正定矩阵Q ∈Rn×n,存在对称正定矩阵P ∈Rn×n,向量q ∈Rn,常数Δ >0满足

引入系统(16)空间
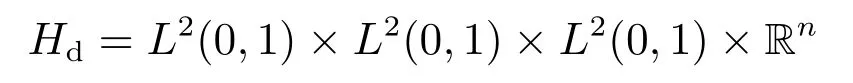
及其上的内积

可将系统(16)写成抽象微分方程形式

则有如下适定性结果.
定理3算子Bd在Hd上生成的半群是收缩的C0半群Td(t).
证很容易看出,算子Bd是稠定闭算子,由直接计算得

进而有Re〈Bdm,m〉≤0,即Bd是耗散算子.此外,利用共轭算子的定义,易于求得

所以,也是耗散算子,进而得出由算子Bd生成的半群Td(t)是收缩半群. 证毕.
这样利用上节同样的分析可知系统(16)是适定的,并且它的唯一解可以由Td(t)Y0给出.此外,显然系统(16)的能量

是相应于上述内积导出的范数,从上述定理的证明还可以看出系统(16)能量的导数满足

为了利用Lyapunov函数法得到系统(16)的指数稳定性,构造Lyapunov函数:Gd(t)=Ed(t)+εφ(t),其中0<ε <1和φ(t)与上节相同.与引理1类似,有如下结果.
引理3Lyapunov函数Gd(t)等价于能量Ed(t),即如下关系成立:
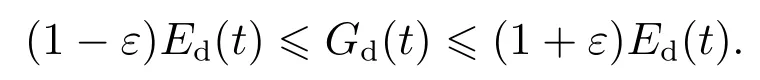
对于系统(16),辅助函数φ(t)具有如下性质.
引理4辅助函数φ(t)满足


定理4系统(16)的能量Ed(t)具有如下指数衰减率

这就是定理中所列的ε需要满足的条件.其次由比较原理可得

最后再根据引理3,得

证毕.
4 H∞边界控制
在本节,受文献[38]的启发,研究系统(1)在负比例反馈控制(2)和动态反馈控制(3)-(4)下内部扰动的H∞控制问题.首先考虑负比例反馈控制是H∞鲁棒的,也就是考虑系统(1)的内部扰动形式:
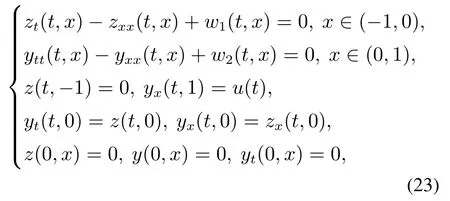
其中w1(t,x),w2(t,x)∈L2(0,∞;L2(0,1))是外部扰动,可容许的外部扰动虽然对受控输出

有影响,但是使得上述系统是内部可稳的.本文所关心的H∞边界控制问题是指,给定γ >0和负比例反馈控制(2),对于所有的可容许外部干扰w1(t,x),w2(t,x),相应的系统(23)和式(2)的解都满足

为了解决上述问题,寻求条件确保下式成立:

这里G(t)是在第2节内定义的,上述关于时间t的导数是对闭环系统(23)和式(2)的解进行的.事实上,如果上式成立,则对上式两侧关于t从0到∞求积分,则有
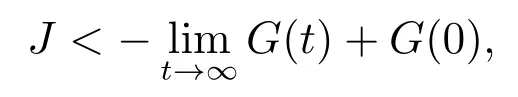
由于G(t)是正定的并且G(0)=0,所以J <0.
现在寻求条件使得式(24)成立.若令Y(t,x)=(z(t,-x),yt,yx,yt(t,1),w1,w2),则仿照(8)的证明,利用Wirtinger不等式(见文献[38]的引理1)和闭环系统(23)和式(2)有


定理5如果选取参数ε,γ和k使得矩阵Ψ是负定的(-Ψ >0),则系统(23)在负比例边界反馈控制式(2)下是H∞鲁棒的.
需要强调的是,一方面,利用MATLAB中LMI工具包很容易验证矩阵Ψ对于什么参数ε,γ和k是负定的;另一方面,利用本节和第3节类似的办法也可给出系统(23)在负比例边界反馈控制(3)-(4)下是H∞鲁棒的充分条件.
5 总结和展望
对于具有边界控制和同位观测的热波耦合系统,当不施加控制时,系统仅是多项式稳定的.为了提升系统的衰减率,本文设计了2种边界反馈,利用直接Lyapunov函数法验证闭环系统是指数稳定的.需要特别指出的是,不但验证2种闭环系统所用到的Lyapunov函数类似,而且系统指数稳定性的验证方法很容易平移用于研究系统关于内部扰动是H∞鲁棒的,从而很容易给出系统是H∞鲁棒的充分条件.然而,除了内部扰动外,边界观测也存在扰动,此时如何设计反馈使其可稳是重要的研究课题,如文献[8,39].此外,利用本文的结果还可以研究系统的一致指数稳定性以及可观性的反问题等.

