二维趋化-Navier-Stokes方程的全局吸引子①

刘婷熙，范小明

西南交通大学 数学学院， 成都 611756

趋化现象最早在文献[1-2]中提出， 描述的是生物学中由于化学物质的影响， 细胞进行定向运动的现象． 众所周知， 细菌细胞一般是生活在各种各样的粘性流体当中的， 所以近十年来趋化-Navier-Stokes方程[3-7]已经成为生物学家和数学家们比较关注的数学模型． 对于趋化-Navier-Stokes方程， 前人关于它在不同边界条件下解的存在情况已有了很多研究[8-12]． 但是对于该系统吸引子的存在性的研究甚少． 本文主要讨论二维有界域下的趋化-Navier-Stokes方程的全局吸引子． 趋化-Navier-Stokes方程如下：

(1)

(2)

(3)

(4)

下面是这个方程的初边值条件：

n(x， 0)=n0(x)，c(x， 0)=c0(x)，u(x， 0)=u0(x)，x∈Ω

在这个模型中，Ω⊂R2是一个带有光滑边界Γ： =∂Ω的有界区域． 其中ν(x)是x∈Γ上的单位外法向量，φ是重力势并且有φ∈L∞(Ω)， Δφ=0，n表示细菌的种群密度，c代表化学浓度，p和u=(u1，u2)分别代表流体的压力和速度． 设n(x，t)，c(x，t)是关于空间和时间t>0的连续函数， 因为c是化学浓度， 故可设

再设f，g可导，f(0)=0，g(0)=0并满足下列条件：

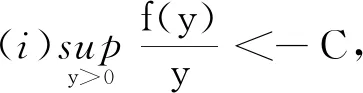
假设细菌和化学物质在一种不可压缩的流体(如水)中求解， 利用Navier-Stokes方程中的速度u来模拟其流动， 由于重力势的存在， 细菌细胞的重量将会影响流体的流动．

本文主要包含了以下几个部分．

第1部分， 给出了半群和吸引子的定义、 吸引子的存在性定理； 讨论了n，c是正解及解的适定性， 从而方程(1)-(4)决定了一个解半群．

第2部分， 证明趋化-Navier-Stokes方程(1)-(4)所对应的解半群在所研究的空间上存在正向不变的有界吸收集． 前人在处理这部分时是将趋化-Navier-Stokes方程看作一个整体来证明其系统的吸收性， 但由于方程(1)-(4)的复杂程度， 采用整体法无法处理其吸收性． 因此我们可以利用此方程的强耦合性， 将它分成3部分来处理． 首先利用能量估计等方法证明化学浓度c的吸收集是存在的， 再从c的吸收集出发证明细菌种群密度n的吸收集存在， 最后由n的吸收性证明了流体速度u的吸收集存在， 综上所述得到了(n，c，u)的吸收集是存在的．

第3部分， 证明方程所对应的解半群是一致渐近紧的． 首先得到u的光滑性， 再利用方程的强耦合性， 通过u的光滑性得到c的光滑性， 再由u的光滑性得到n的光滑性， 最后利用半群性质， 得到解半群在所研究的空间上是一致渐近紧的．

1 预备知识

本章节将会给出一些证明所需的基本定义和定理．

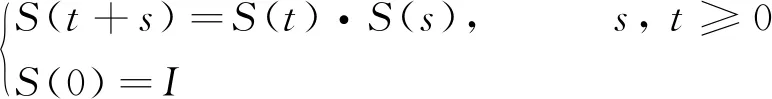
则称S(t)为算子半群．

定义2[13]如果紧集A满足下面的条件：

1) 不变性： A是半群S(t)作用下的不变集， 即S(t)A=A， ∀t≥0；

2) 吸收性： A吸收H上的所有有界集． 即对于任意一个有界集B∈H， 这里的B满足

3) A有一个开邻域U， 使得对于U上的任意一个n0， 当t→∞时， 所有从n0出来的轨迹S(t)n0都收敛到A． 即当t→∞时， dist(S(t)n0， A)→∞， 则称这个紧集A为半群S(t)的一个吸引子． 如果A还吸收相空间H， 则称A为全局吸引子．

引理1[13]设{S(t)}t≥0是一个算子半群， U⊂H是一个开集， 并且

1) B是U上的一个吸收集；

2)S(t)是一致紧的(对于充分大的t)， 则B的ω-极限集A=ω(B)是U上的一个紧的全局吸引子．

引理2若(n，c，u)是方程(1)-(4)在Ω×[0，T]， ∀T>0中的弱解， 则

n(x，t)>0，c(x，t)>0 a． e． (x，t)∈Ω×[0，T]

证由文献[12]可知方程(1)-(4)在没有f(n)，g(c)这两项时， 它的解n(x，t)>0，c(x，t)>0是成立的， 则可以推出

其中A(t)=-u·+Δ-(c·+Δc)， 所以因此有

又因为f(0)=0， 所以由中值定理可以得到

则

同理可证c(x，t)>0．

‖u‖Lq(Ω)≤C‖u‖Lp(Ω)

其中

该定理给出了解的适定性， 其证明主要利用Faedo-Galerkin方法[13]， 与文献[11]类似， 本文不做过多赘述． 再结合引理2， 我们得到n，c>0．

由定理1足以在空间H上定义连续的算子半群{S(t)}t≥0：

下面将利用文献[13-15]证明在空间H上半群{S(t)}t≥0存在全局吸引子A．

2 H上吸收集的存在性

首先证明在H上存在有界吸收集， 其过程需要在相应的空间中对解进行估计．

引理5设B1是L2(Ω)中的任一有界集，c是从B1中出发的方程(2)的一个解． 存在常数γ1>0和时间t1=t1(B1)>0， 当t≥t1时，

证由条件(ii)可得存在常数β∈(0，λ1)和充分大的正常数K1， 使得

g(c)≤(λ1-β)c+K1

(5)

对方程(2)的两边分别与c作L2(Ω)的内积

由(5)式得

(6)

(7)

(8)

对(8)式使用Gronwall不等式， 有

(9)

引理6设B2是L2(Ω)中的任一有界集，n是从B2中出发的方程(1)的一个解． 存在常数γ2>0和时间t2=t2(B2)>0， 当t≥t2时，

证设L2(Ω)上一球形邻域包含B1， 其圆心为零点， 半径为γ1． 由引理5知，c从L2(Ω)的有界集出发， 在时刻t1后将一直在有界集B1中． 不妨设c总在B1中．

对方程(1)的两边分别与n作L2(Ω)的内积， 得到

由化学浓度c的有界性和连续性得

再由条件(i)可得f(n)≤-Cn+K1，K1是一个充分大的常数， 则

对K1‖n‖L1使用Young不等式得

因此

(10)

由Gronwall不等式得

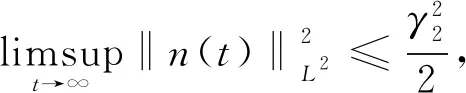
(11)

证设L2(Ω)上一球形邻域包含B2， 其圆心为零点， 半径为γ2， 由引理6知，n从L2(Ω)的有界集出发， 在时刻t1+t2后仍在有界集B2中． 不妨设总在B2中．

此时压力项将会消失， 得到

(12)

由(19)式

利用Gronwall不等式，

(13)

综合(9)， (11)， (13)式可以得到在H上以零点为圆心，RB=γ1+γ2+γ3为半径的有界闭球B=B(0，RB)是(n，c，u)的有界吸收集， 且是正向不变的， 即H上任意有界集B⊆B(0，RB)， 经过时间t*=t1+t2+t3后， (n，c，u)进入B中且不再离开． 故由引理5- 7得到．

定理2方程(1)-(4)生成的解半群{S(t)}t≥0在空间H上存在正向不变的有界吸收集．

3 解半群{S(t)}t≥0一致渐近紧

设B是{S(t)}t≥0在H中的正向不变集． 设(n，c，u)是方程(1)-(4)的整体解． 现证明从B出发， 方程的解最终都进入K的有界集， 从而得到解半群{S(t)}t≥0是一致渐近紧的．

引理8∀r>0， 存在常数γ4(r)>0， 当t≥r时， 有

证对(12)式从t到t+r上积分， 有

(14)

让方程(3)在Ω上与-Δu作内积， 得

利用引理4和Young不等式

再利用(13)式可得

(15)

(16)

由(15)，(16)式得

根据(11)式得

这意味着对所有的t≥r，

(17)

引理9∀r>0， 存在常数γ5(r)>0， 当t≥r时， 有

证将(7)式从t到t+r上积分， 有

(18)

让方程(2)在Ω上与-Δc作内积得

利用Young不等式、 Hölder不等式和引理3得

由(17)式可得

(19)

(20)

结合(19)-(20)式得到如下不等式

(21)

对(21)式从0到r上积分

由(18)式得

这意味着对所有的t≥r

(22)

引理10∀r>0， 存在常数γ6(r)>0， 当t≥r时， 有

证对(10)式从t到t+r上积分， 有

由(11)式可得

(23)

让方程(1)在Ω上与-Δn作内积

利用Young不等式、 Hölder不等式和引理3

(24)

由(17)和(24)式可得

(25)

这里C4是一个充分大的正常数．

(26)

(27)

由(25)-(27)式可得

(28)

对(28)式从0到r积分， 得

由(23)式得

这意味着对所有的t≥r，

(29)

定理3方程(1)-(4)生成的解半群{S(t)}t≥0是一致渐近紧的．

证设K上以零点为圆心，RM=γ4+γ5+γ6为半径的有界闭球M=B(0，RM)． 由引理8、 引理9和引理10知(n，c，u)从H中的正向不变集B出发， 经过时间r后， 进入K中的有界集M． 而K紧嵌入到H中， 从而得到解半群{S(t)}t≥0在H中是一致渐近紧的． 证毕．

由定理2和定理3以及引理1得到方程(1)-(4)在H上存在紧的全局吸引子．