一种基于CORDIC 算法的高精度反正切求解*

仲雅莉 ，吴俊辉 ，刘炫 ，高萍 ,3，段晓辉 ，4

(1.国家超级计算无锡中心，江苏 无锡 214072；2;江南大学，江苏 无锡 214122；3.山东大学，山东 济南 250100；4.清华大学，北京 100084)

0 引言

坐标旋转计算机(Coordinated Rotation Digital Computer，CORDIC）算法只有移位和加减运算，便于在FPGA 等硬件平台上实现复杂的三角函数、双曲函数、指数函数和复数求模等计算，广泛应用于数字鉴相、数字上下变频、波形产生、快速傅里叶变换等方面[1-4]。

针对CORDIC 算法中由于迭代次数多、输出延时大和精度较低等问题，国内外很多学者进行了研究和改进。文献[5]提出了基于自适应旋转角度的CORDIC 算法，该算法虽然减少了迭代次数，但每次迭代都需要额外判断，增加了实现难度。文献[6]提出了将查找表和传统CORDIC 算法相融合，通过查找表将角度值细化，通过数学量化分析，根据细化后的较小角度补码，直接按位值进行角度单向旋转，该算法随着对精度要求的提高，查找表存储空间大大增加，硬件资源消耗巨大。文献[7]提出了一种基于最佳一致逼近方法的幅度与相位补偿算法，第一步是利用传统的CORDIC 算法迭代数次后得到向量信息，第二步是采用最佳逼近法进行多项式补偿，该算法虽然提高了精度，但逼近算法需要存储多项式系数，硬件资源消耗较大。文献[8]提出来一种基于CORDIC 算法的反正切函数计算的改进算法，该算法对累加器中因截尾而产生的误差做了算法改进，仅增加了运算速度，精度并未明显提高。文献[9]提出了一种基于查找表的改进的CORDIC 算法，该方法通过缩减有效数据位宽、合并迭代等手段节省了剩余角度Z 的计算量，该算法把迭代次数进行拆分，用了14 次迭代和查找表的结合，硬件资源消耗较多，性能提升却不足。

在分子动力学模拟中[10-11]，成键力的计算引入了三角函数。常见的一种情况是从三维坐标计算角度，通常需要根据sinθ 和cosθ 的值求解反正切，该应用场景下对反正切的精度要求较高，传统的CORDIC 算法很难满足[12-13]。

本文在文献[7]的基础上，简化逼近算法，提出了一种改进算法，测得不采用函数拟合也可得到高精度的剩余相位跟踪，从而有效提高了CORDIC 求反正切算法的精度，降低了延时，减少了电路面积。

1 CORDIC 算法基本原理

在X-Y 坐标平面上将向量(x0，y0)逆向旋转角度θ 得到向量(x1，y1)，如图1 所示。两向量间坐标变换关系为：

图1 向量旋转示意图

两边同时除以cosθ，可得到伪旋转方程，即：

除以cosθ 后，旋转角度还是正确的，但向量的模长发生了变化。

CORDIC 求反正切的本质就是从坐标(x0，y0)开始旋转，每次旋转固定角度θi，旋转方向为di=sign(y(i))，旋转的目标是纵坐标yi趋近于0，进行N 步迭代，则有反正切角。为了能够简化运算部件，CORDIC算法常采用每一小步的旋转角度θi满足tanθi=2-i，从而可以通过简单移位来完成乘法运算，因此原始的算法可以简化为迭代移位相加算法，迭代方程为：

如果需要保持向量的模长，则可以通过加入旋转补偿因子K 实现。当N 确定时，经历N 次迭代后的K 是一个常数：

该补偿因子常在求三角函数sin 和cos 时使用。

2 基于CORDIC 求反正切的算法改进

对CORDIC 算法进行分析可以看出，θi=arctan2-i。而进行i 次迭代后，残余的角度的绝对值即是求反正切值时的误差。定义εi为第i 次旋转后的误差，则：

所以CORDIC 求反正切算法在残余角度较小时的误差以每次1 bit 的速度收敛。对于定点数而言，即每次迭代使得精度收敛1 bit。以在进行均匀取样仿真了不同迭代次数下的CORDIC 最大误差如表1 所示，对于相位精度要求极高的场景，如果要达到10-9数量级，需要迭代28 次，其带来的硬件资源消耗和时延都是不可承受的。

表1 不同迭代次数下CORDIC 算法的最大误差

2.1 使用sinε 逼近ε

当CORDIC 经过第N 次旋转之后，设其估计的角度剩余误差为ε，显然：

即N 次迭代后的残余误差小于2-(N-1)。根据微积分中正弦函数的极限，有：

所以使用sinε 来逼近ε 是一种有潜力降低误差的手段。

由于sinε 与ε 在ε 比较小时非常接近，一种可以考虑的方案是直接采用sinε 来代替ε。该方案的误差可以通过泰勒展开进行估计，ε-sinε 在ε=0 处展开可得：

也就是说，sinε 和ε 的差值以三次方的速度缩小，比直接CORDIC的收敛速度快得多。当ε接近2-9≈1.95×10-3时，从式(9)可以估计出ε-sinε≈1.24×10-9，意味着用CORDIC算法迭代10次后，反正切的误差约为1.95×10-3，而使用sinε 对反正切结果进行校正后，误差降为约1.24×10-9。

实验的结果可以与上述估计相吻合：令err=ε-sinε，画出曲线如图2所示，可以看出ε越小，ε与sinε的差值越小。当ε＜2-9时，ε与sinε的差值可达到10-9数量级，这也意味着当CORDIC迭代10次后，残余的ε足够小，可以用sinε的值代替ε的值来修正CORDIC 的结果。

图2 区间[2-14，2-3]上的ε-sinε(对数坐标轴)

根据上述对误差的论证，在一定迭代步数后采用sinε 代替ε 是安全的，如果输入的初始向量已经在单位圆上，那么最终向量的纵坐标即为sinε。所以本文对应修改了CORDIC 求反正切的算法，如算法1 所示。

算法1输入在x 轴正半轴单位圆上的改进CORDIC算法

在迭代步数N 的选取上，可以根据式(7)和式(9)，按照所需的误差t 来对N 进行选取：

而对于普通的CORDIC 算法，第N 步的误差约为2-(N-1)，则需要：

从式(11)和式(12)可以看出，在需求精度较高的情况下，本文改进的CORDIC 算法只需要大约三分之一的迭代步就能实现与原有的CORDIC 相似的精度。

2.2 sinε 的计算

根据CORDIC 的原理可知，CORDIC 的旋转过程中向量模长会发生变化，需要对模长进行修正。设迭代初始向量为(x0，y0)，经过N 步旋转后，根据式(3)得到(xN，yN)，zN，式(4)可求得旋转修正因子K 使得：

当(x0，y0)在单位圆上时，如图3 所示，l=1，yN即为sinε，这就可以解决输入的坐标在单位圆上的问题。

图3 (x0，y0)在单位圆上时的余角

若输入的坐标(x0，y0)不在单位圆上，则需要根据式(14)进行模值归一化：

从而使得：

如式(14)所示，模值归一化引入了平方根倒数，直接求解资源消耗大。可以用牛顿迭代法求得，迭代公式如式(17)所示，其中p 是式(14)中初始坐标(x0，y0)的模值平方，q 是对其平方根倒数的估计。

在定点数实现牛顿迭代法时，由于没有尾码对齐的性质[14]，因此很难通过简单的变换就获得一个良好的初值[15]。本文考虑将p 映射到[1，4)之间，如式(18)所示：

其中22k和2k均可通过移位实现。当p'落在[1，4)之间时，可以分段通过线性变换获得一个较为良好的初值：

式(19)中初值与结果的误差基本可以控制在2×10-2以内，如图4 所示。这样只需两步牛顿迭代就可以获得较为准确的。由于CORDIC 旋转与模值无依赖性，模值归一化流程仅在最后一步将s 与Kyn相乘时会导致额外的一次乘法的时延。

图4 初值q0与之差

2.3 整体架构

改进的CORDIC 求反正切算法整体架构如图5 所示。其中，角度预处理是指把坐标转换到第一或第四象限，预处理后的坐标先按照传统CORDIC 进行N 级迭代，再根据式(16)进行纵坐标修正和误差补偿，最后结果映射还原到原始象限的角度。算法2 展示了该架构对应的伪代码。

图5 改进的CORDIC 算法的整体流程

算法2整体的CORDIC 算法架构

2.4 改进算法在分子动力学模拟中的应用

在分子动力学模拟中，常见的一种情况是从三维坐标计算角度。以分子动力学中的二面角ϕ 为例，很多实现就选择了使用sinϕ 和cosϕ 作为二维反正切函数的输入，从而获得值域为[-π，π)的结果。此时由于坐标显然在单位圆上，模长归一化的过程就可以省略。

图6 展示了求解平面ijk 和jkl 间二面角ϕ 所需的向量，r 是两个原子间的向量，n 是平面的法向量。其中：

图6 二面角求解时的向量

n'是nijk和njkl所确定的平面上与nijk垂直的向量：

其二维视图如图7 所示。这样，ϕ 的计算方式为：

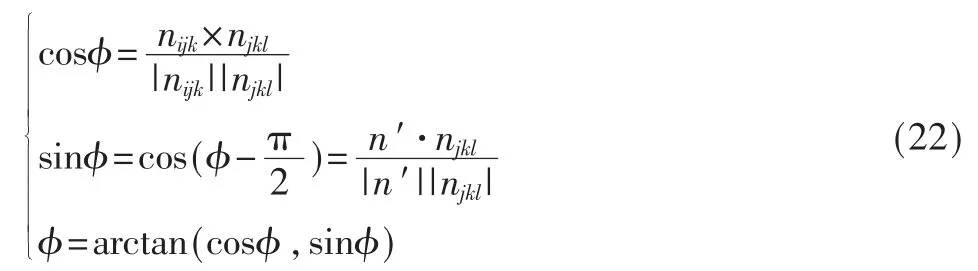
图7 图6 中几个向量的二维视图

也就是说此处的模长归一化已经隐含在了二面角计算的流程中，从而可以省略反正切函数的模长归一化过程。

类似地，在CHARMM 键角的计算中：

这里V是键角的势能，K和θ0是经验参数，θ是两个键形成键角的角度，对于以i 原子为中心，j、k 构成的键角，一般以反余弦函数求解：

计算原子受力F 时需要根据链式法则求解V 对三个原子坐标x 的梯度，以j 原子为例：

也就是说，cosθ 本来就需要计算，通过对计算流程进行修改后即可避免反正切函数进行模长归一化的过程。

综上所述，虽然在必要时可以利用牛顿迭代法实现模长归一化的过程，但是在分子动力学等求解具体计算几何问题的情境下，基本不需要额外的模长归一化实现。此时，改进的CORIDC 算法可以更好地发挥其优势。

3 算法仿真和分析

将传统CORDIC 求反正切算法和改进的CORDIC 求反正切算法分别用MATLAB 建模仿真，并与理论值进行了误差分析。输入数据的横坐标和纵坐标分别以0.001为间隔遍历[-1，1]，统计相同迭代次数下所有数据的最大绝对误差，性能曲线如图8 所示。可以看出改进后的CORDIC 算法性能提升明显，在迭代10 次的情况下，精度从10-3数量级提升到10-9数量级。

图8 改进CORDIC 算法与传统CORDIC 算法的误差比较

本研究采用Verilog HDL 语言进行设计，并在Xilinx公司的Virtex UltraScale+HBM VCU128 型号FPGA 上完成了电路实现。整个模块的设计采用了32 bit(3 bit 整数位+29 bit 小数位)的定点化输入输出。在保证绝对误差小于5×10-9的前提下，比较了硬件资源消耗如表2 所示。

表2 改进CORDIC 算法与传统CORDIC 算法的资源消耗对比

对于需要模值归一化的应用场景，归一化处理引入了DSP 资源的消耗，但查找表(Look Up Table，LUT)资源消耗降低了64.8%，触发器(Flip-Flop，FF)资源消耗降低了35.3%，输出时延降低了53.3%。对于无模值归一化应用场景，LUT 资源消耗降低了64.3%，FF 资源消耗降低了61.6%，输出时延降低了60%。改进的CORDIC 算法在硬件消耗和时延方面有明显优势。

4 结论

针对传统CORDIC 求反正切函数硬件资源消耗大，迭代次数多等问题，实现了一种改进的CORDIC 算法计算反正切函数的解法。在保证与传统CORDIC 算法精度数量级相同的情况下，减少了算法迭代次数，用旋转后的纵坐标补偿了相位，从而显著提高了算法运算速度。采用32 bit 定点的硬件实现，在保证相同计算精度的前提下，改进CORDIC 算法的硬件资源消耗和时延方面均有明显降低。算法仿真和FPGA 实际测试结果表明，改进后的CORDIC 算法适用于高速高精度场合。

该设计在包含模长归一化实现时已经比经典的CORDIC 算法拥有更短的延时，在很多计算几何的具体问题中，可以通过对计算流程的适当重构从而使用单位向量作为输入，从而可以进一步降低该设计的开销，尤其适合分子动力学等三维空间中需要使用计算几何方法求解的问题。