基于MCMC的无线传感器网络目标定位算法

张沛朋，李冬锋

(1.济源职业技术学院 艺术设计系，河南 济源 459000； 2.华北水利水电大学 信息工程学院，河南 郑州 450045)

0 引 言

由于在智能交通、目标跟踪等军事和民用领域的广泛应用，基于时延-多普勒频率的无线传感器网络(wireless sensor networks，WSN)目标定位问题近年来备受关注[1-4]。针对该问题，现有算法可分成两类：两步定位和直接定位(direct position determination，DPD)。两步定位的基本框架是：第一步从接收信号中提取时延[5,6]和多普勒[7,8]参数；第二步基于时延-多普勒，估计目标位置参数[7,8]。两步定位会损失一部分有用信息，导致最终目标定位误差增大，特别是在信噪比或信号采样点数较低时。近年来，随着通信带宽和芯片计算能力的提升，直接定位开始得到关注，并发展出一系列有效算法[9-15]，这类直接定位算法的思路是从接收信号中直接估计出目标位置参数，无需提取中间定位参数，避免了额外的信息损失，因此比传统两步定位具有更高的精度和稳健性。然而，上述直接定位算法[9-15]存在计算复杂度过高、初值依赖和局部收敛问题，特别是对于目标位置-速度估计这样的高维问题求解。

为提高基于时延-多普勒的WSN目标定位的精度、稳健性和计算效率，本文提出一种基于马尔科夫链-蒙特卡罗(Markov-chain Monte-Carlo，MCMC)[16-18]的直接定位算法。首先从传感器接收信号中推导目标位置和速度估计的优化函数，然后将其转化为目标位置和速度的分布函数，利用MCMC方法对分布函数抽样，通过统计样本均值得到目标位置和速度估计值。最后通过计算机仿真实验将估计结果与现有算法对比，突出本文算法的性能优势。

1 定位场景与信号模型

本文考虑的WSN运动目标定位场景如图1所示。

图1 WSN目标定位场景

根据上述场景假设，目标与传感器节点m在第k个时隙内的距离及其变化率可以表示为

(1)

(2)

rm,k(t)=am,kxk(t-τm,k)eι2πfm,kt+wm,k(t)

(3)

假设以频率fs对各传感器接收信号进行采样，得到式(3)的离散形式如下

rm,k(n)=am,kxk(n-τm,kfs)eι2πfm,kn/fs+wm,k(n)

(4)

式中：n=0,1,…,N-1，N为每个时隙内的采样点数。

定义如下向量

n=[0,1,…,N-1]T

(5)

rm,k=[rm,k(0),rm,k(1),…,rm,k(N-1)]T

(6)

xk=[xk(0),xk(1),…,xk(N-1)]T

(7)

Dm,k=diag{eι2πfm,kn/fs}

(8)

Γm,k=diag{e-ι2πfsnτm,k/N}

(9)

F=[e-ι2π(0)n/N,e-ι2π(1)n/N,…,e-ι2π(N-1)n/N]T

(10)

wm,k=[wm,k(0),wm,k(1),…,wm,k(N-1)]T

(11)

则传感器节点m在第k个时隙内接收到的目标基带信号可以表示为如下的向量形式

rm,k=am,kHm,kxk+wm,k

(12)

其中，Hm,k=Dm,kFHΓm,kF，m=1,2,…,M，k=1,2,…,K。

2 基于MCMC的直接定位算法

为了以较低的计算复杂度实现对目标位置和速度的估计，本节提出一种基于MCMC的直接定位算法。算法具体过程如下。

2.1 直接定位优化函数构建

(13)

(14)

式(14)中的未知参量中，含有冗余参数am,k， 其最大似然估计为

(15)

(16)

(17)

(18)

那么，目标位置和速度的估计可以通过式(18)中目标函数的极大化得到。

2.2 目标位置参数求解

2.2.1 优化函数全局最大化

根据Pincus提出的优化理论[19]，式(18)中θ的估计问题可以转化为如下积分形式

(19)

(20)

(21)

根据伯努利大数定律，当随机样本数量Ns足够大时，式(21)的数值运算结果即可收敛至式(19)积分结果。至此，积分问题被转化为了从概率密度函数pρ(θ) 中产生随机样本，也即pρ(θ) 的抽样问题。然而，由于pρ(θ) 的形式比较复杂，因此要从pρ(θ) 抽取样本并不容易，而MCMC方法就是为此目的而诞生的。

2.2.2 MCMC方法

MCMC方法由两个MC组成：第一个“MC”为“马尔科夫链(Markov Chain)”缩写，意为利用马尔科夫链从目标分布中抽样；第二个“MC”为“蒙特卡罗(Monte Carlo)”缩写，意为根据抽取的样本，利用蒙特卡罗方法对积分进行计算。具体来说，在MCMC方法中，首先建立一个马尔科夫链，使得目标分布pρ(θ) 为其平稳分布p(θ)， 即p(θ)=pρ(θ)， 然后运行此马尔科夫链充分长时间直至其收敛至平稳分布p(θ)， 那么从达到平稳分布的马尔科夫链中产生样本，即可实现对目标分布pρ(θ) 的抽样。Metropolis-Hastings抽样是一类常用的构造马尔科夫链的方法，包括了Metropolis抽样、Gibbs抽样等。对于一维随机变量θ， Metropolis抽样的基本流程如下：

(1)构造提议分布q(·|θ(l))；

(2)在待估参数空间内初始化马尔科夫链的状态θ(0)；

(3)对于l=0,1,2,…,重复以下过程进行抽样：

1)从提议分布q(·|θ(l)) 中产生候选状态θ*；

2)生成均匀分布随机数u～(0,1)；

3)若u<α(θ(l),θ*)， 其中α(θ(l),θ*) 为接受概率

(22)

则将马尔科夫链状态转移至候选状态，即令θ(l+1)=θ*； 否则马尔科夫链维持当前状态，即令θ(l+1)=θ(l)。

4)增加l， 返回到步骤1)。

上述过程中，提议分布q(·|θ(l)) 应为一个程序可抽样的分布，通常可用随机游走法构造。随机游走法假设候选状态θ*从一个对称的提议分布q(θ*|θ(l)) 中产生，即在每一次迭代中，从提议分布中产生增量Δθ，然后令θ*=θ(l)+Δθ。 典型地，可用高斯分布产生增量Δθ， 此时候选状态服从高斯分布θ*～增量方差对生成马尔科夫链的效果有重要影响。一般来说，增量方差过大，会导致大部分候选样本被拒绝，此时算法效率很低。如果增量方差过小，则候选样本几乎都被接受或拒绝，链几乎不再游走，同样效率较低。一般来说，接受率在0.5～0.85才能保证得到的马尔科夫链具有较好的性质[20]。为此，可以设置增量方差的调节参数，并在游走过程中监视马尔科夫链的接受率，以使算法达到预设的接受率。

(23)

(24)

生成均匀分布随机数u～(0,1)： 若令否则令

2.2.3 基于MCMC的目标位置参数求解

基于上述MCMC方法，对于本文WSN目标定位问题，待估参数为目标位置和速度参数构成的2dim×1维列向量，因此本文采用Gibbs抽样生成马尔科夫链，采用随机游走法构造提议函数。算法具体实现过程如下：

(1)设置状态转移次数阈值Nb(保证马尔科夫链收敛)，需要的样本数量Ns；

(3)令l=0，j=1， 重复如下抽样过程：

1)利用随机游走法构造提议分布

(25)

4)生成随机数u～(0,1)：

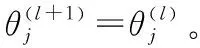
5)调整随机游走步长：

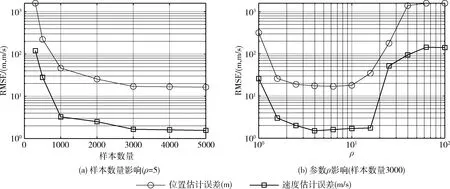
6)如果j

7)如果l

(4)根据抽取的样本θ(0),θ(1),…,θ(Nb+Ns)， 估计目标位置和速度参数的估计值

(26)

3 克拉美罗界分析

(27)

其中， Re(·) 和Im(·) 分别表示复数的实部和虚部。那么，由式(13)中向量r的概率密度函数，可得待估参数的Fisher信息矩阵为

(28)

式中：H表示矩阵共轭转置运算。根据待估参量φ的构成，偏导矩阵∂r/∂φT可以表示为

(29)

根据复变函数求导规则，式(29)右侧子矩阵可以表示为

(30)

(31)

J2=diag{J2,1,J2,2,…,J2,K}

(32)

J2,k=diag{H1,kxk,H2,kxk,…,HM,kxk}

(33)

(34)

(35)

Λ1=ι2πdiag{n}

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

根据克拉美罗界的定义，待估参量φ的CRLB为Fisher信息矩阵的逆，即

CRLB(φ)=[FIM(φ)]-1

(44)

4 仿真实验

(45)

载频fc=10 MHz。 目标信号能够同时被WSN的M=4个传感器节点所接收。每个传感器节点在K=50个时隙段对目标辐射的电磁信号进行接收和采样，采样频率为fs=1 MHz， 每个时隙段持续时间为T=1 ms， 接收信号的幅度am,k=1。 WSN各传感器节点的位置和速度见表1。为了模拟实际的信号数据，我们为各传感器节点接收信号添加零均值的高斯白噪声，噪声方差根据仿真实验场景调整。

算法的估计性能通过500次独立计算机仿真实验统计得到的目标位置和速度均方根误差(root mean square error，RMSE)来衡量，定义如下

(46)

(47)

表1 传感器节点位置和速度

首先，为了直观展示本文所提算法的有效性，我们设置噪声方差σ2=1， 然后利用本文所提算法对目标进行定位，算法的目标函数如图2所示。

图2 目标函数

从图2(a)可以看出，目标信号在其真实位置参数处得到峰值，并且得益于多个时隙的长时间信号能量积累，原本淹没在噪声中的目标信号数据积累后的峰值远高于周围噪声。从图2(b)中可以看到，通过调整参数ρ的值，目标函数的峰值被进一步强化，噪声被一定程度抑制，这将有利于后续MCMC方法抽样。

本文算法利用MCMC方法抽取样本的效果如图3所示。

图3 MCMC方法抽样(ρ=5)

从图3中生成的马尔科夫链可以看到，抽样过程开始后，随机游走的增量方差较大，体现在马尔科夫链的路径步长较大。较大的步长有利于马尔科夫链迅速遍历参数空间，并快速收敛至平稳分布。收敛至平稳分布后，马尔科夫链的样本在目标位置参数附近游走，步长较小。对生成样本统计发现，MCMC抽样的接受率在0.7左右，说明了生成马尔科夫链具有较好的性质。

如上文所示，本文所提算法涉及到的两个重要参数——样本数量和参数ρ。接下来通过仿真实验分析样本数量和参数ρ对定位精度的影响。仿真实验结果如图4所示。

图4 MCMC方法参数对定位精度的影响

首先，为定量分析样本数量对目标定位精度的影响，并确定样本数量的最优选取，我们统计了不同样本数量下的目标位置和速度估计RMSE，结果如图4(a)所示。从图4(a)可以看到，与直观预期一致，整体上随着样本数量的增加，目标位置和速度估计的RMSE呈下降趋势。然而，当样本数量增加至3000以后，目标位置和速度估计的RMSE下降速度趋近于0，此时再增加样本数量将无法显著提高目标位置和速度的估计精度，反而会增加计算复杂度。因此，对于本文所设置的定位场景，样本数量设置为3000为宜，后续仿真实验亦如此设置。

然后，为了确定参数ρ的合理取值，我们在不同的参数ρ下进行定位仿真，并统计目标位置和速度估计RMSE，结果如图4(b)所示。从图4(b)可以看到，在参数ρ的取值较小时，与前文所述一致，增大参数ρ的值可以显著提高目标位置和速度的估计精度，这是因为一个较大的ρ可以抑制噪声影响，使得目标分布峰值更加尖锐，继而使得生成样本更加集中于目标位置处；然而，当参数ρ取值过大时，也会导致目标位置和速度的估计精度降低，这是因为参数ρ取值过大会导致目标分布峰值过于尖锐，从而导致MCMC抽样困难，并且参数ρ取值越大意味着指数运算次数越高，计算复杂度越高。因此，对于本文定位场景，参数ρ取值为10左右为宜。后续仿真实验中设置为ρ=10。

接下来，为了评估算法在不同信噪比条件下的定位性能，我们将各传感器节点接收信号添加不同方差的噪声，从而得到不同信噪比的接收信号，并在不同的信噪比条件下利用本文算法进行仿真定位实验。为了突出本文算法的定位性能，我们将现有5种算法，包括文献[7]中传统的两步定位方法、文献[9]中基于网格搜索的直接定位算法(DPD-GS)、文献[13]中基于期望最大化的直接定位算法(DPD-EM)、文献[14]中基于粒子滤波的直接定位算法(DPD-PF)、文献[15]中基于改进粒子滤波的直接定位算法(DPD-MPF)，作为对比算法。对比结果如图5所示。

图5 不同信噪比条件下算法的定位精度比较

图5中结果表明，随着接收信号信噪比的提升，几种算法的定位精度总体上也都随之提升，但几种算法的定位精度却不尽相同。传统的两步定位算法由于其两步处理体制会损失一部分信息，导致最终目标位置和速度估计RMSE始终明显高于其余几种直接定位算法以及CRLB。DPD-GS算法通过网格搜索确定目标位置和速度参数，定位精度受到搜索网格大小的限制，在高信噪比条件下定位精度无法进一步提高。DPD-EM算法通过期望最大化迭代算法确定目标位置和速度参数，在高信噪比条件下定位精度可以接近CRLB，但是当信噪比较低时，目标位置和速度估计RMSE高于DPD-PF、DPD-MPF以及本文DPD-MCMC算法，这说明了期望最大化算法作为一种局部最优算法，在低信噪比条件下的稳健性较差。DPD-PF算法和DPD-MPF算法的定位性能相当，总体上定位误差略高于本文DPD-MCMC算法。本文DPD-MCMC算法的定位误差要低于现有几种算法，并且在一般的信噪比条件下定位精度可以达到CRLB。

算法的平均运行时间也是衡量算法性能的重要指标。因此，我们在相同的计算机仿真环境下比较了现有算法的平均运行时间。计算机仿真环境配置如下：电脑Lenovo ThinkCentre M920t；内存32 GB；处理器Intel I9-9900(8核，3.1 GHz)；操作系统Win10 64位专业版；软件：MATLAB R2019b。仿真结果见表2。

表2 算法计算复杂度比较

表2中6种算法的平均运行时间比较结果表明，直接定位算法的计算复杂度要高于传统的两步定位算法，但是直接定位算法可以得到更高的定位精度。在几种直接定位算法的比较中，本文DPD-MCMC算法的计算复杂度要显著低于DPD-GS、DPD-PF、DPD-MPF算法，与DPD-EM算法相当。这是由于本文DPD-MCMC算法通过MCMC方法获取参数样本，继而利用样本统计结果实现目标位置和速度参数估计的方式，无需像DPD-GS算法那样在多维空间内进行网格搜索，也无需像DPD-PF和DPD-MPF算法那样产生大量粒子，有效降低了计算复杂度。需要指出的是，虽然本文DPD-MCMC算法在本文仿真环境下平均需要2.68 s时间才能估计出目标位置和速度，但是利用更为专业和强大的计算平台，运行时间有望进一步缩短至可对目标实时定位的程度。

5 结束语

本文提出了一种针对无线传感器网络的目标直接定位方法。首先依据最大似然准则推导了基于时延和多普勒频率的运动目标直接定位数学优化模型。针对该模型以矩阵特征值的形式给出而难以解析求解的问题，提出了一种基于马尔科夫链-蒙特卡罗的数值求解方法。此外，本文推导了基于时延和多普勒频率的无线传感器网络目标定位克拉美罗界，从理论上分析了算法定位误差的理论极限。计算机仿真实验结果表明：相比于传统的两步定位方法，本文算法具有更高的定位精度；相比于现有的直接定位算法，本文算法的计算复杂度更低，并且在一般信噪比条件下，定位性能能够逼近克拉美罗界。