有限群的正规子群

王雪影， 乔守红

(广东工业大学数学与统计学院，广州 510520)

1 引 言

本文所考虑的群都是有限群，下面所提到的群G总是有限群.

在有限群理论中，极大子群对有限群结构的影响是显著的. 我们知道，群G是幂零群的充要条件是G的每个极大子群在G中都是正规的；G是超可解群当且仅当G的每个极大子群在G中的指数是素数. 对于可解性，参考文献[1]介绍了子群的c-正规性，并且证明了G是可解群的充要条件是G的任意的极大子群在G中c-正规.

定义1[1]设H是群G的子群. 称H在G中c-正规，如果存在G的正规子群T，使得G=HT且H∩T≤HG，其中HG表示包含在H中的G的极大正规子群.

用u来表示超可解群系，Zu(G)表示G的超可解超中心，G的所有正规子群H的乘积使得在H下的所有G-主因子皆为素数阶循环群；Zu Φ(G)表示G的非Frattini超可解超中心，G的所有正规子群H的乘积使得在H下的所有非Frattini-G-主因子都为素数阶循环群. 用|G|表示群G的阶数；G/K表示群G关于正规子群K的商群；N∶M表示子群N被子群M扩张.

2007年， Ahmad， Jaraden和Skiba给出了c-正规子群定义的一种推广[2].

定义2[2]设H是群G的子群.称H是G的uc-正规子群，若存在G的次正规子群T使得G=HT且(H∩T)HG/HG≤Zu(G/HG).

在参考文献[2]中，作者证明了如下的结果.

定理1设F是包含u的饱和群系，E是群G的正规子群满足G/E∈F.如果E的每个非循环的Sylow子群的极大子群在G中有一个超可解的补(supplement)或是uc-正规的，则G∈F.

一般来说，对于群G，子群Zu Φ(G)比子群Zu(G)要大一些. 在本文中，用Zu Φ(G)替换Zu(G)，给出以下子群的嵌入性质.

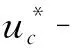
注 在定义1-2中，可以规定T包含HG替换T被THG表示.故在定义3中，直接假设“T包含HG”.

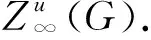
2 预备知识

本节列出一些后面证明中用到的引理.

引理1[3]设H◁G，H1和H2是H的G-主因子系，则H1和H2的主因子是一一对应的，并且使得对应的主因子是G-同构，从而G中的H1的Frattini主因子和H2的Frattini主因子相对应.

引理2[3]设Z=ZF Φ(G)，N和T皆为G的正规子群，F是某群类，则

(i)Z的每个非-Frattini-G-主因子在G中是F-中心；

(ii)ZN/N≤ZF Φ(G/N)；

(iii) 如果TN/N≤ZF Φ(G/N)且(|T|，|N|)=1，则T≤Z.

引理3[4]设U，V和W是G的子群，则下列表述等价

(i)U∩VW=(U∩V)(U∩W)；

(ii)UV∩UW=U(V∩W).

下面这个引理是由Wielandt给出来的.

引理4[4]设G是有限群，U◁◁G，则Soc(G)≤NG(U).

引理5设G是一个群，则有

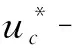
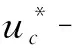
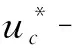
(H/K∩T/K)/(H/K)G/K≤Zu Φ((G/K)/(H/K)G/K).

因为(H/K∩T/K)/(H/K)G/K=((H∩T)/K)/(HG/K)且

Zu Φ((G/K)/(H/K)G/K)=Zu Φ((G/K)/(HG/K))，

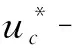
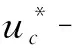
T∩HK=K(T∩H)≤HZ，

这里Z/HG∶=Zu Φ(G/HG).通过G-同构，下列式子成立

KZ/KHG=KHGZ/KHG≅Z/KHG∩Z=Z/HG(Z∩K).

再由引理1得出KZ/KHG≤Zu Φ(G/KHG).记X/KHG∶=Zu Φ(G/KHG).则

(T∩KH)/KHG≤HZ/KHG≤Zu Φ(G/KHG).

由于HGK≤(HK)G，所以(T(HK)G∩KH)/(KH)G≤Zu Φ(G/(KH)G).显然，

G=(KH)(T(KH)G) 且T(KH)G◁◁G.

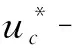
证假设N不是Φ(G)的子群. 下面证明N是p阶的. 设L/N◁P/N且L/N的阶为p，那么存在一个元素a∈L/N，使得L=N〈a〉，ap∈N.如果N=Φ(L)，那么L是循环群，从而N也是循环群，从而|N|=p.接下来讨论Φ(L)

(T∩S〈a〉)/(S〈a〉)G≤Zu Φ(G/(S〈a〉)G).

如果N∩Op(G)=1，那么N的阶数为p.假设N≤Op(G)，那么S≤N≤Op(G)≤T，从而

S(S〈a〉)G/(S〈a〉)G≤Zu Φ(G/(S〈a〉)G).

若S(S〈a〉)G/(S〈a〉)G=1，则S≤(S〈a〉)G，因此S≤(S〈a〉)G∩N.这意味着S=1且|N|=p.如果S(S〈a〉)G/(S〈a〉)G≠1，则有

S(S〈a〉)G/(S〈a〉)G≤(N(S〈a〉)G/(S〈a〉)G)∩ZΦ(G/(S〈a〉)G).

因此

N≅N(S〈a〉)G/(S〈a〉)G≤Zu Φ(G/(S〈a〉)G).

因为N是非-Frattini子群，所以|N|=p.

引理7[5]令G为有限群，N是G的极小正规子群，M是G的极大子群. 如果G=N∶M且M可解，那么G可解.

3 主要结果

证只需要证明定理的必要性. 假设结论不真且G是一个极小阶反例.

步骤1设N是G的极小的正规子群，则G/N超可解. 因此N是G的唯一的极小正规子群.

下面证明G/N满足定理的假设. 设M/N是PN/N的一个极大子群，显然对于P的某个极大子群P1有M=P1N，其中P是G的非循环的Sylow子群. 由此可知P∩N=P1∩N是N的一个Sylow子群. 根据假设，G有次正规子群T，并且T包含(P1)G，使得G=P1T且

(P1∩T)/(P1)G≤Zu Φ(G/(P1)G).

从而有

G/N=(M/N)(TN/N)=(P1N/N)(TN/N)，

显然TN/N◁◁G/N.因为

(|N∶P1∩N|，|N∶T∩N|)=1，

所以

(P1∩N)(T∩N)=N=N∩G=N∩(P1T).

根据引理3得出

(P1N)∩(TN)=(P1∩T)N.

由于N◁G，因此N(P1)G≤(NP1)G且(P1N/N)G/N=(P1N)G/N.又因为

黄羊、黄鹿、桂花和巧云听到动静，慌忙跑过来，见伯父哭成这样，彼此交换了眼神，都没有上前去劝住他；直到黄石趴在地上，轻轻地咽呜，才过去扶他进屋去。桃花绞了块热毛巾，细细地给父亲擦脸和洗手。黄方永拉起黄石的手，轻轻地摇道：“爷爷，爷爷，不哭噢；我以后不骑马了。”他那奶声奶气的童音，惹得大家洇红了眼睛，黄石更是泪如雨下，一把抱起孙子，哽咽道：“宝宝呀，宝宝呀……”伯父总算清醒了，黄羊和黄鹿安排伯父躺下去后，就领着桂花和巧云回家了。

(P1∩T)/(P1)G≤Zu Φ(G/(P1)G)，

于是

(P1∩T)N/(P1N)G≤Zu Φ(G/(P1N)G).

从而

(P1N/N∩TN/N)/(P1N/N)G/N=(P1∩T)N/N/(P1N)G/N≤Zu Φ(G/N/(P1N)G/N).

步骤2NΦ(G)且N非循环.

假设NΦ(G)或N是循环群. 由步骤1，G超可解.

步骤3若对于任意的整除|G|的素数p有Op(G)=1，因此Zu Φ(G)=1.

若否，存在素数p使得Op(G)≠1，那么由步骤1可得N≤Op(G).根据步骤2，P是非循环的群，且NΦ(P).我们选择P的极大子群P1，使得P=NP1.由假设可知P1在G中正规，则因此存在T◁◁G且(P1)G≤T，使得

G=P1T， (P1∩T)/(P1)G≤Zu Φ(G/(P1)G).

因为N是唯一的，所以(P1)G=1，从而P1∩T≤Zu Φ(G).

步骤4存在G的Sylow-子群P使得1≠N∩P

显然，G非单群. 因此，N

步骤5最终矛盾.

定理得证.

设N是G的任意极小正规子群. 因为亚幂零群类是饱和群系，请见参考文献 [6]，所以N是G唯一的极小正规子群且Φ(G)=1.继而可得CG(N)=N是p-子群，其中p为某素数.

如果Zu Φ(G)≠1，由于Φ(G)=1，则N≤Zu Φ(G)是p阶子群. 存在G的极大子群M，使得G=N∶M，那么M≅G/N≅G/CG(N)且M为交换群. 因此，G超可解，故G是亚幂零群.

下面假设Zu Φ(G)=1.设Q是G的Sylowq-子群，则QG=1.由假设，存在T◁◁G，使得G=QT且Q∩T≤Zu Φ(G)=1.因为T是G的次正规的Hall子群，所以T◁G.由于Φ(G)=1且G的Sylowp-子群在G中正规，因此N是G的Sylow子群. 从而G=N∶M，其中M是幂零的.

定理的必要性显然可得.

定理4设G可解当且仅当G有可解的极大子群M满足：存在T◁◁G使得G=MT并且(M∩T)/MG≤ZS(G/MG)，这里S表示可解群系.

证仅需要证明定理的充分性. 对G的阶数进行归纳，证明G是可解的.

步骤1MG=1.

显然，G/MG满足定理的假设. 如果MG≠1，通过归纳假设知G/MG是可解的. 因为M可解，所以得到G可解. 因此，我们可以假设MG=1.

步骤2ZS(G)=1.

若ZS(G)≠1，取G的极小正规子群N包含于ZS(G)，则N是交换群. 由于MG=1，故G=N∶M可解. 因此，ZS(G)=1.

步骤3完成证明.

根据定理条件，存在T◁◁G，使得G=MT且M∩T≤ZS(G)=1.若T=G，那么M=1，故G的阶为素数，从而G可解. 假设T

下面假设M∩N≠1.从而N不包含于T.令N=T1×T2×…×Tk，其中这些Ti是非交换的同构单群. 由于1≠N∩T◁◁N，可以假设N∩T=T1×T2×…×Tl.由于N是G的极小正规子群，且G=MN，则M共轭作用在集合{T1，T2，…，Tk}上是传递的. 再根据M∩T=1，可推出

M∩T1=M∩T2=…=M∩Tl=1，

根据M在{T1，T2，…，Tk}上的传递性，那么M∩Ti=1，其中i=1，2，…，k.

考虑G右乘作用在陪集空间[G∶M]上，作用是本原的. 记α=M，则Gα=M，Nα=M∩N.如果Nα=M∩N在Ti上的投影不是满射，由参考文献[7]，得到

M∩N=R1×R2×…×Rk，

其中Ri真包含于Ti，矛盾于M∩T=1.因此M∩N=Nα在Ti上的投影是满射. 从而Ti是可解的，最后的矛盾. 证毕.

推论1[8]有限群可解的充要条件是存在一个c-正规的可解极大子群.

4 总 结

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.