一类高阶非线性分数阶多点边值问题解的存在性
刘 畅,王文霞
(太原师范学院 数学系,山西 晋中 030619)
0 引言
分数阶微积分的概念是整数阶微积分到任意阶的推广。相比于整数阶导数,分数阶导数可以更好地描述过程的记忆性和遗传性。分数阶微分方程在自动控制、航天技术、信号识别、生物数学、物理学、力学等领域广泛应用。
分数阶微分方程边值问题近年来备受关注,见文献[1~4]。在不同边界条件下的微分方程解的存在性是分数阶微分方程理论研究的一个重要领域,见文献[5~8]。近年来一些作者研究了高阶分数阶微分方程的边值问题,见文献[9~11]。
文献[9]研究了如下分数阶微分方程m点边值问题正解的存在性:
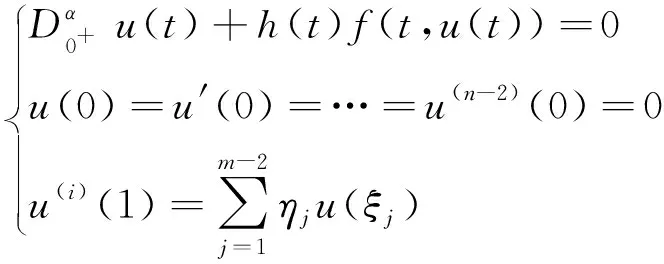
(1)
其中i≥0是整数,n为整数,i≤n-2,α≥2,0 文献[10]研究了如下非线性项依赖未知函数的分数阶导数,且具有非线性边界条件的分数阶微分方程的边值问题: (2) 其中n>3,1≤γ≤β≤n-2,f∶[0,1]×[0,∞)×[0,∞)→[0,∞),g∶[0,1]×[0,∞)→[0,∞),k∶[0,∞)→[0,∞)是连续函数。作者运用了锥上的不动点理论,得到了边值问题(2)的唯一正解存在的充分条件。 文献[11]研究了如下分数阶微分方程无穷点边值问题: (3) 其中α>2,n-1<α≤n,i∈[1,n-2]是整数,αj≥0,0<ξ1<ξ2<…<ξj-1<ξj<…<1 (j=1,2,…)。作者运用Schauder不动点定理,建立了边值问题(3)正解的存在性定理。进一步,利用凹算子的不动点定理给出了边值问题正解的存在唯一性结果。 受上述文献启发,本文研究如下高阶非线性分数阶微分方程多点边值问题: (4) 其中n>3,1<γ≤β≤n-2,j∈[1,n-2]是整数,0≤ξ≤1,0<η≤1,a,b,λ,μ都为正数,f∶[0,1]××→,g∶→是连续函数,是Riemann-Liouville导数。 本文运用Leray-Schauder非线性抉择原理,讨论边值问题(4)解的存在性的充分条件。 定义1[1]连续函数f∶(0,+∞)→的α>0阶Riemann-Liouville分数积分定义为 其中,等式的右端在(0,+∞)有定义。 定义2[1]连续函数f∶(0,+∞)→的α>0阶Riemann-Liouville分数导数定义为 其中n=min{m∈∶m≥α},等式的右端在(0,+∞)有定义。 引理1[1]假设u∈C(0,1)∩L(0,1)有α>0阶导数属于C(0,1)∩L(0,1).则 ci∈,i=1,2,…,n,其中n大于或等于α的最小整数。 引理2 若h(t)∈C[0,1],则下面边值问题 有唯一解x(t)且 其中 证明 由引理1,将微分方程转化为等价的积分方程 于是 由xi(0)=0得,cn=cn-1=cn-2=…=c2=0.即 则 于是 故 因此我们得到 证毕。 引理3 函数G(t,s)满足以下性质: 1)G(t,s)在[0,1]×[0,1]上是连续的; 2) ∀(t,s)∈[0,1]×[0,1],有 证明 由G(t,s)在表达式可知结论1)成立。以下证明结论2)成立。 ∀(t,s)∈[0,1]有 证毕。 类似于引理3的证明可得 我们引入如下记号 下是一个Banach空间。 定义算子T∶E→E如下 则 引理4[4](Leray-Schauder非线性抉择原理)设F是Banach空间,Ω⊂F是凸的,且0∈Ω.若T∶Ω→Ω是一个全连续算子,则下列结论至少有一个成立: i)算子T在Ω上有一个不动点, ii)集合E={x∈Ω∶x=λT(x),0<λ<1}是无界的。 本文将用到如下假设: H1)存在非负函数ω(t),φ(t)∈L1[0,1],使得 |f(t,u,ν)|≤ω(t)|u|+φ(t)|ν|,∀t∈[0,1],u∈+,ν∈+ 且 注2 若条件H2)满足,则存在k>0,使得 |g(x)|≤k 定理1 假设H1),H2)成立,则算子T∶E→E全连续。 证明 首先证明T∶E→E是连续的。 由条件H1)可知 <2l[ω(s)+φ(s)] 由Lebesgue控制收敛定理可知, 于是由条件H1)、H2)和注1可得, 故有 设Ω为E中的有界集,则存在常数r>0,使得 以下证明T(Ω)是相对紧的.对任意的x∈Ω有 此外,因为G(t,s),G1(t,s)在(t,s)∈[0,1]×[0,1]上一致连续,所以∀ε>0,∃δ>0,使得当t1,t2∈[0,1],|t1-t2|<δ时有 进而对∀x∈Ω有 <ε <ε 即TΩ等度连续。 由Arzela-Ascoli定理可知,算子T∶E→E是全连续算子。证毕。 定理2 假设条件H1)、H2)满足,则边值问题(4)在E上至少有一个解。 证明 设X={x∈E|x=λTx,λ∈(0,1)},由引理4可知只需证明集合x是有界的。当x∈X时x=λTx,对∀t∈(0,1)有 |x(t)|=|λTx(t)|≤|Tx(t)| 因此 故集合X有界。由引理4可知算子T至少有一个不动点,则边值问题(4)至少有一个解。 例 考虑下面边值问题 显然有 通过简单计算可知,Γ(α)≈11.632,Γ(α-β)=1,Γ(α-γ)=2,进而有 故 于是定理2条件都满足,所以边值问题(4)至少存在一个解。 Existence of solutions for a class of higher order nonlinear fractional multipoint boundary value problems LIU Chang,WANG Wen-xia


1 预备知识和引理

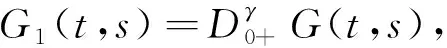

2 主要结果











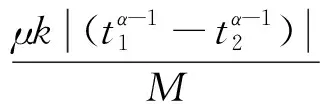
3 示例


