非线性-积分抛物型方程零阶项的识别问题

许瑶瑶，杨 柳

（兰州交通大学 数理学院，兰州 730070）

数理物理方程反问题是以具有物理背景的偏微分方程（组）作为研究的主要对象，它与其他数学分支及物理、化学等自然科学和工程技术的很多领域都有着广泛的联系［1］.众所周知，正问题的求解过程一般是由条件推导出结果.对于正问题而言只要条件充分，那么正问题的解必然存在且唯一.对于反问题的求解过程来说，它是一个逆向的，因此反问题的研究难度非常大.我们应该指出正问题和反问题之间有一个主要的区别是在Hadamard意义上，正问题是适定的，而大多数反问题是不适定的［2］，即反问题的解是不存在，不唯一或不稳定的.因此为解决反问题的不适定性，大多会采用正则化［3］和最优控制等理论方法来解决.例如文献［4］中的方程：

使用Tikhonov正则化方法，识别椭圆型方程Dirichlet问题中系数q（x）的收敛速度.文献［5］考虑一个二阶抛物型方程反演辐射系数的初边值问题：

其中ϕ（x）是区间（0，1）上给定的一个光滑曲线，q（x）是所要反演的系数，假设给定如下附加条件：u（0，T）=f（x），x∈（0，1）利用最优控制的方法确定满足问题的u和q.文献［6］研究期权定价中著名的Black-Scholes方程：

主要基于最优控制理论利用市场观测数据重构隐含波动率σ的反问题，文献［7］基于极值原理讨论退化抛物型方程的源系数反演问题，文献［8］在最优控制的框架下分析带有积分源项的抛物型方程的反源问题，证明解的存在性、唯一性和稳定性.文献［9］主要运用最优控制方法来考虑具有积分型源项的二阶抛物型方程的初值反演问题.通过阅读相关文献可知对于非线性带积分型源项的抛物型方程的系数反演问题的研究较少，在实际应用中如污水治理、污染物挥发等都会遇到这一类的问题.

本文研究当终端观测数据已知时，重构非线性-积分抛物型方程的零阶项识别问题，该问题P可描述为如下形式：

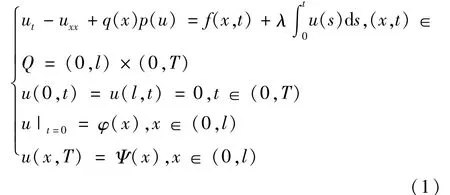
其中：f（x），φ（x），Ψ（x），p是（0，l）上已知的光滑函数，Ψ（x）表示在终端时刻T＞0时的观测值，φ（x）是初始时刻的观测值.如何确定满足问题P的u和q（x）？

本文主要是从理论分析的角度出发对问题P进行研究，由于问题P的不适定性，可转化为一个新的控制问题来代替原来的问题P.

1 最优控制问题

这里我们假设φ（x）＞0，φ∈C2，α［0，l］，0＜α＜1且Φ=maxx∈［o，l］|φ（x）|.在方程（1）中，假设函数p∈C2［0，Φ］并且p满足Lipschitz条件：

以及p（0）=0，|p′|，|p″|≤L，且q（x）是有界函数，即|q（x）|≤c，考虑到问题（1）的不适定性，以及对于一般终端观测数据Ψ（x），问题P可能没有解，我们转而考虑以下问题P1如下所示.

问题P1求，使得

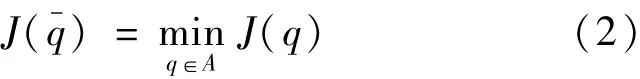
这里

A=｛q（x）|0＜α0≤q≤α1，▽q∈L2（0，l）｝U（x，T，q）是问题（2）的解，q（x）=A，N是正则化参数，α0，α1是两个给定的正常数.

引理1.1［10］假设φ∈C2，α［0，l］，0＜α＜1，对于∀q（x）∈A，问题存在唯一解

引理1.2假设φ（x）∈L2［0，l］，对q（x）∈L2（0，l），存在一个与T和M有关的非负常数C满足下式

证明根据问题（1），对于0＜t≤T，有

即

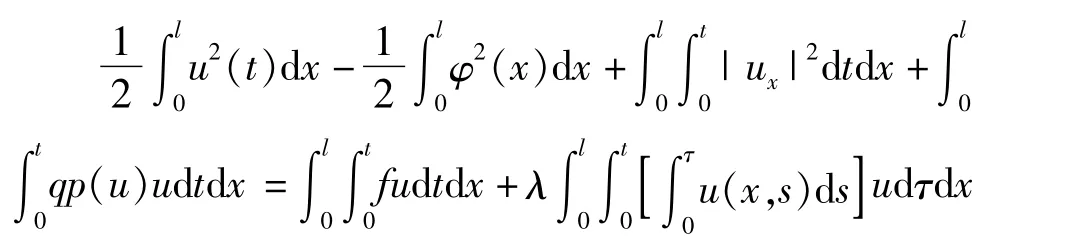
又因为

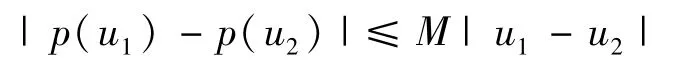
那么

这里|q|=abs（q）

又因为

因此

即

由Gronwall’s不等式得

引理1.2得证.

2 存在性

定理2.1 存在一个J（q）的极小元q∈A，即

定理2.1的证明是标准的，可参考文献［11-13］.

3 必要性

定理3.1 若q为最优控制问题（2）的解，则存在一个三元函数（u，v；q）满足以下方程

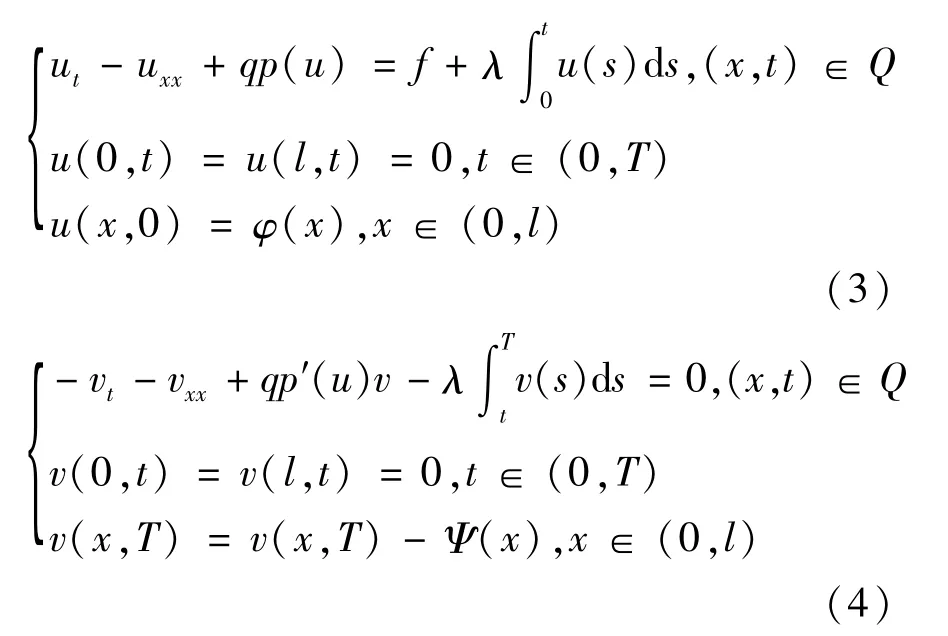
且对于∀h∈A有

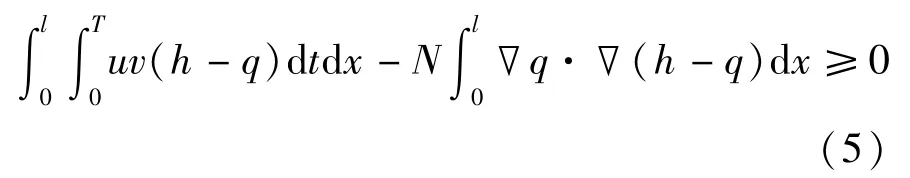
证明对于∀h∈A，0≤δ≤1，令

则

令uδ是方程（1）的解，其中q=qδ从而有

由式（7）可得

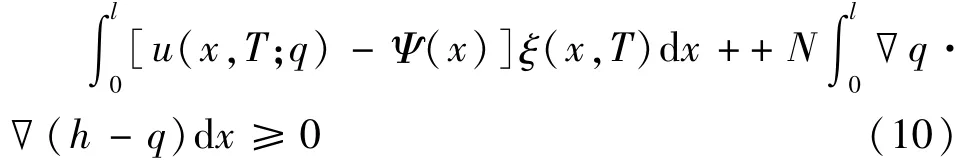
假设v是以下问题的解

其中L*是L的共轭算子，

由式（9）和（11），可得

所以

由式（10）和（12）可得

定理3.1得证.

4 局部唯一性和稳定性

由于最优控制问题P1的控制泛函是非凸的，故不存在全局唯一解，但当T足够小时，可以证明P1的解具有局部唯一性和稳定性.

引理4.1对于任意有界连续函数h（x）∈C（0，l），有

这里的x0是（0，l）上的不动点.

证明对于0＜x＜l

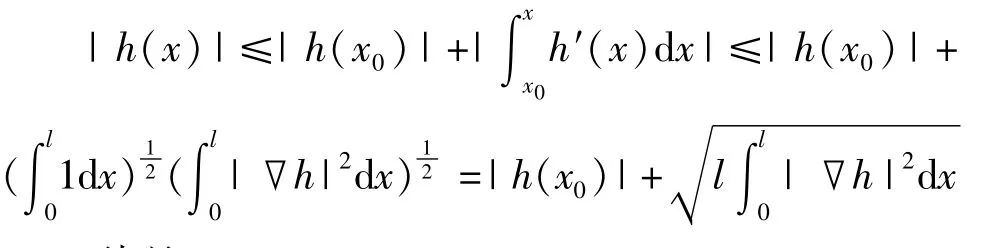
引理4.1得证.

引理4.2对于方程（4）由极值原理可得

引理4.2的证明是标准的.

引理4.3［14］设u（x，t）∈C2（Q）∩C（）是问题（1）的解，则有如下估计

在这一节中，本文证明解的局部唯一性和稳定性.假设Ψ1（x），Ψ2（x）是给定的函数，并满足Ψ（x）∈C［0，l］.令q1（x）是问题P1对应的Ψ1（x）的极小元，q2（x）是问题P1对应的Ψ2（x）的极小元，｛ui，vi｝分别是当q=qi时（i=1，2）问题（3）和（4）的解，令u1-u2=U，v1-v2=Λ，q1-q2=Q.因此U和Λ满足

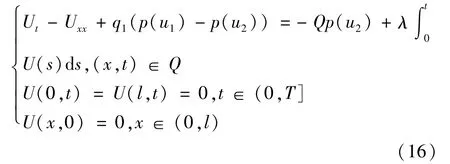
引理4.4对于方程（16），有以下估计

证明有0≤θ≤1

从方程（16）中，有0＜t≤T

则有

即

整理得

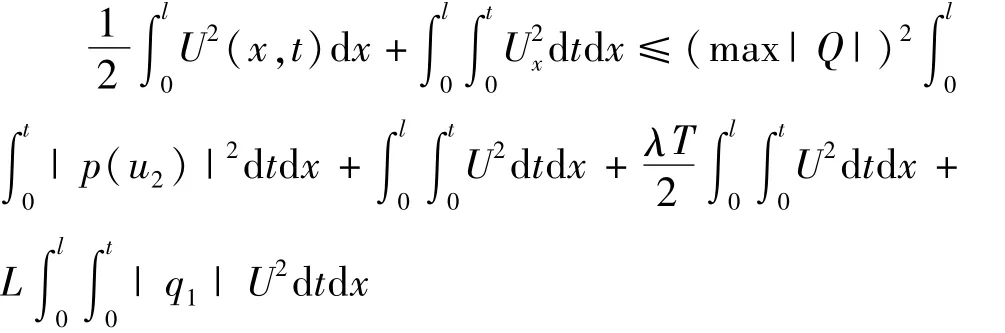
其中|q1|为q1的绝对值.

从而有

由Gronwall’s不等式得

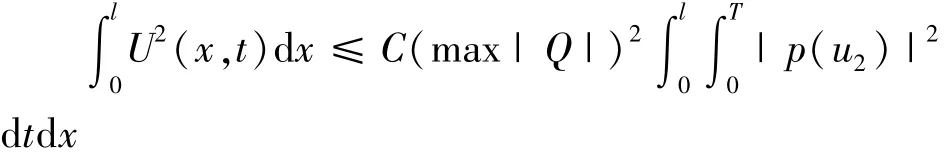
其中：C是与T无关的常数.

引理4.4得证.

引理4.5由方程（17）可得如下估计

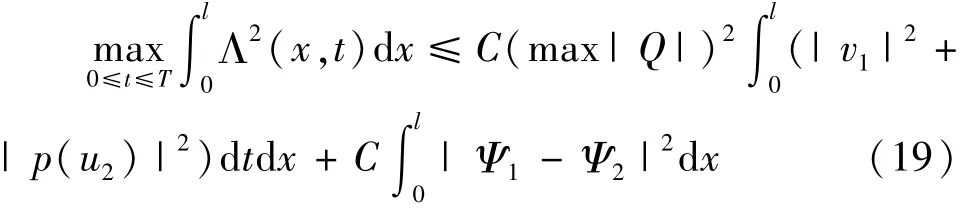
证明由方程（17）可得

通过积分可得

即

从P满足的条件可知

从而有

又因P是光滑函数，有

由引理4.2和Cauchy不等式得

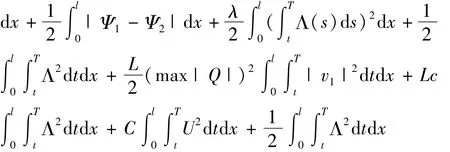
结合式（18）可得

由Gronwall’s不等式可得

引理4.5得证.

定理4.6令q1（x），q2（x）是最优控制问题P1的两个最小值，如果存在x0∈（0，l），使q1（x0）=q2（x0），这里T≪1，C是不依赖T，l，N的常数，有以下估计

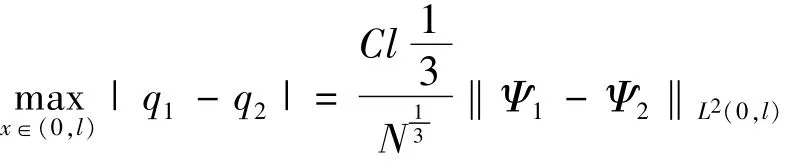
证明在式（5）中，当q=qi时取h=q2，当q=q2时取h=q1，则有

当q=qi（i=1，2）时，｛ui，vi｝（i=1，2）分别是式（3）和（4）的解

由式（20）和（21）得

即

由定理4.6假设知存在x0∈（0，l）使

由引理4.1知

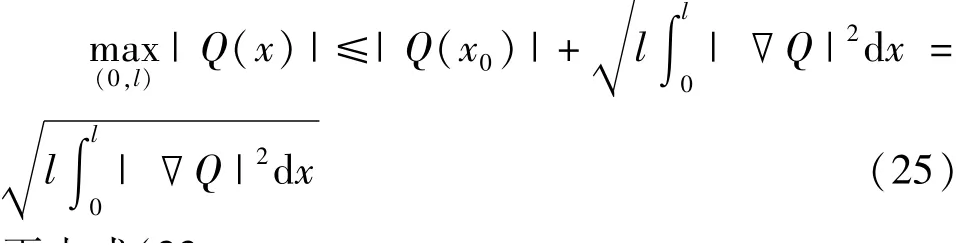
再由式（23），（25）和Young不等式可得

由引理4.2和4.3可知

又因为p（u）是有界函数，故

则

当T≪1时，使

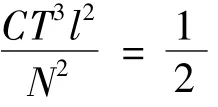
则

定理4.6得证.

注：极小元的唯一性是定理4.6的直接推论，正则化参数的选取会对反问题的研究产生影响.由定理4.6容易得到如果存在误差界δ，令N→0，δ→0，则，那么最优控制的解是局部稳定且唯一的.

5 结论

本文主要是在最优控制理论框架下，研究当终端观测数据已知时，反演非线性-积分抛物型方程零阶项q=q（x）的识别问题.并通过建立控制泛函，完成了对控制泛函极小元的存在性、必要性、局部唯一性和稳定性的证明.本文着重于对一维情况下进行理论分析，将在后续工作中考虑对此模型在二维情况甚至更高维情况下进行研究，将其应用到实际生活的问题当中，实现研究的价值.