基于改进修正Barzilai-Borwein迭代大规模MIMO信号检测算法

代 涛,李正权,2,王舟明

(1.江南大学 物联网工程学院,江苏 无锡 214122;2.江苏省未来网络创新研究院,江苏 南京 211111)

大规模多输入多输出(MIMO, multiple-input multiple-output)技术具有数据传输速率高、信道容量大[1]的显著优势,能够扩大信号传输范围,提高通信质量,因此是未来无线通信领域的研究热点。在功率受限情况下,信号传输实时性和精确度无法满足数据业务应用需求,故大规模MIMO上行链路中需引入快速准确的信号检测技术以提升系统性能,但基站端有海量天线,会使信号检测运算复杂度大幅增加,因而亟待设计一种高性能且复杂度低的信号检测算法。

一般来说,信号检测算法可以分为非线性检测和线性检测两种类型。常见的非线性检测算法有最大似然(maximum likelihood, ML)检测算法[2],它可以实现最佳的性能,但其复杂度随着天线数呈指数增加,难以应用于大规模MIMO系统。为了得到复杂度低并且接近ML算法性能的非线性算法,文献[3]提出了消息传递(message passing,MP),文献[4]提出了期望传播(expectation propagation,EP),但在天线数量很高或者调制阶数很高时,其实现复杂度依然不小。在大规模MIMO系统中,天线的数量一般要比用户的数量大很多,每个用户之间的信道近似正交,会出现信道硬化现象[5]。由于这个特性,一些线性检测算法可以得到很好的检测性能,与此同时信号处理方式也更为简便,常用的有迫零(forced zero,ZF)检测算法[6],不过ZF算法没有考虑噪声影响,尤其当信噪比较低时其误码率性能差。为此，提出了最小均方误差(minimum mean square error,MMSE)算法[7],但ZF和MMSE都带来了高维矩阵求逆的问题。

对于高维矩阵求逆问题,典型算法可以分为两类:一类是基于级数展开替代矩阵求逆典型算法。文献[8]提出了Neumann级数近似算法,该算法将矩阵求逆转换为一系列的矩阵向量乘法。然而,复杂度的降低并不明显,尤其当Neumann级数阶数高于2时,算法的复杂度仍高达O(K3),并且随着用户数的增加,性能明显下降。另一类是使用迭代替代矩阵求逆，将MMSE检测中求逆问题转化为求解线性方程组问题,通过迭代算法求解线性方程组。Richardson迭代[9]虽然实现复杂度较低,但是算法收敛速度慢;还有高斯赛德尔(GS, Gauss-Seidel)[10]、连续超松弛(SOR, successive over relaxation)[11]、Kaczmarz[12]算法等,这些方法的计算步骤之间有很高的关联性,只能按顺序进行计算,并且存在初始的收敛性较差问题。因此,研究者提出了一些检测方法来提高计算的并行性。Jacobi算法[13]是一种简单的迭代算法,具有很高的并行性,但是算法依然存在初始收敛性较差的缺点。而最速下降法(steepest descent,SD)[14]在初始更新就可以得到较好的收敛性,通过为算法提供有效搜索方向,来使得算法收敛加快。不过传统最速下降法步长固定,相对比下Barzilai-Borwein算法[15]是沿着最速下降的方向,来选择合适步长以进行迭代,提高算法性能。因此在实际的应用中可以得到更好的性能。文献[16]提出Barzilai-Borwein和最速下降法结合的一种信号检测算法(SDBB),虽然性能得到提升,但该算法并没有选取一个合适的初值,来提高算法的收敛速度,与此同时对步长选取没有进行更细致的考虑。文献[17]对上述算法进行了分析和证明,描述为CBB算法,为防止出现歧义,下文统称SDBB算法为CBB。

文中通过对文献[16]算法进行改进来解决信号检测问题,通过对该算法设置一个合适的初值,通过对不同步长进行了仿真,分析出更加合适的步长。仿真结果证明,对于Barzilai-Borwein算法的性能随着天线数量增加而明显下降的问题,所提出的改进算法在适应不同数量的用户方面更有效率,同时算法在误码率性能方面优于Barzilai-Borwein和CBB算法。该算法在误码率方面可以接近MMSE,同时又避免复杂度过高的问题。同时该算法在无创微波成像[18]中也被应用。

文中的其余部分组织如下:第1节介绍了大规模MIMO和信号检测的系统模型;第2节介绍了MMSE信号检测算法、Barzilai-Borwein迭代算法以及所提算法;第3节对不同算法的复杂性进行分析对比;第4节对MMSE、Barzilai-Borwein、CBB算法、改进修正Barzilai-Borwein算法进行了误码率性能仿真;最后,在第5节中得出结论。

1 系统模型

如图1,大规模MIMO系统中,假设接收端有N根天线,发送端有K个用户,每个用户配备单个天线,一般情况下N≥K。

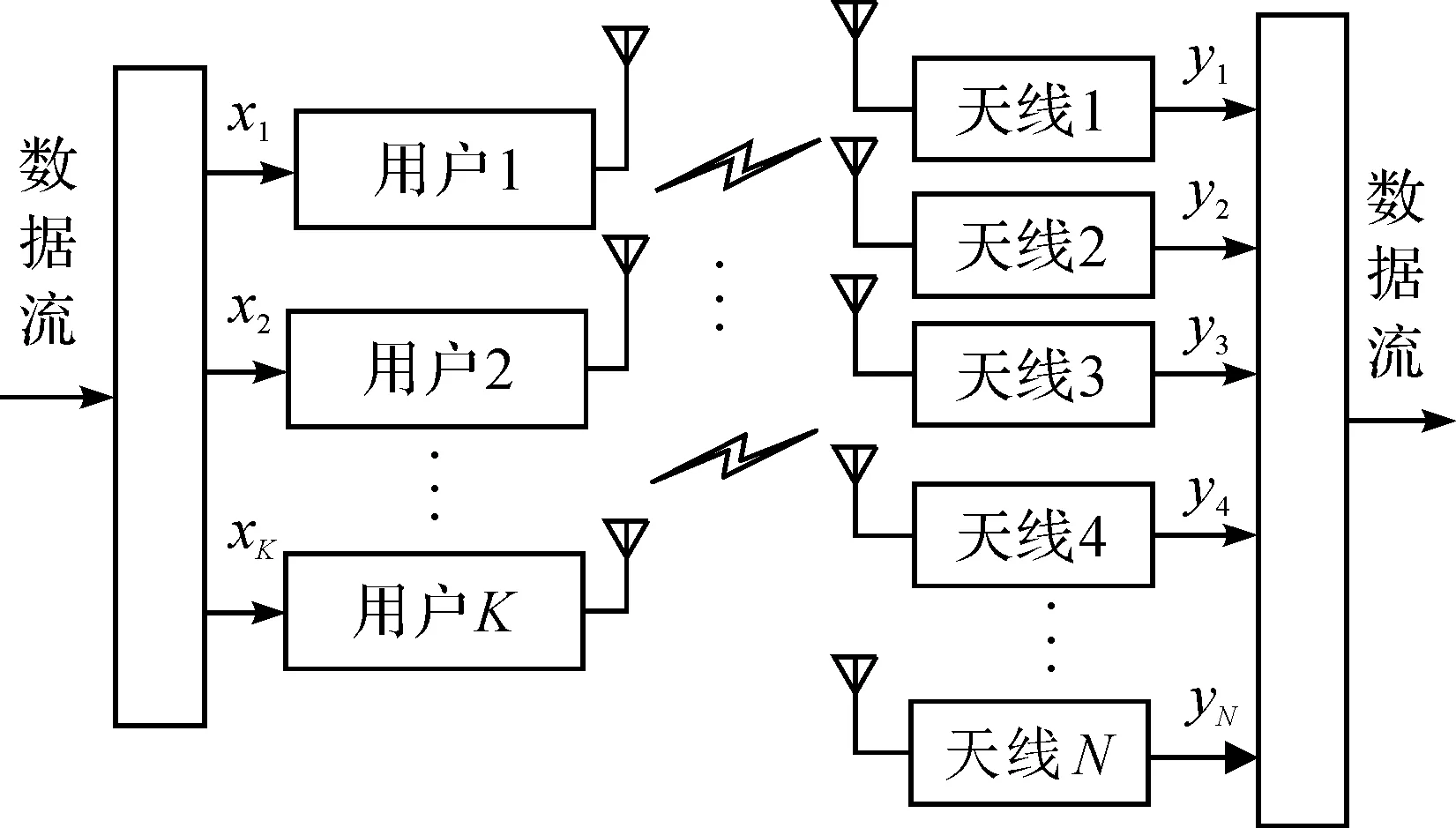
图1 大规模MIMO系统模型

大规模MIMO系统接收端信号yC可以表示为

yC=HCxC+nC。

(1)

文中,假设每个用户使用单根天线,同时每个用户功率设置为E|xi|2=1,xi∈Q,其中Q代表调制符号集。xC=[x1,x2,…,xK]T∈CK×1表示K个用户同时发送的经过调制以后的符号,信号经过的是瑞利衰落信道,信道增益矩阵[19]为HC=[h1,h2,…,hK]∈CN×K,信道增益向量为hj=[h1,j,h2,j,…,hN,j]T∈CN×1,hi,j表示第j个发送天线与第i个接收天线之间的信道衰落系数,与此同时hi,j是满足均值为0,方差为1的复高斯分布。其中nC=[n1,n2,…,nN]∈CN×1表示N维的加性高斯白噪声(additive white Gaussian noise,AWGN),ni满足均值为0,方差为σ2。

为了对数据进行分析处理,将复数信道模型HC转换为实数信道模型,同时对发送信号xC,接收信号yC以及噪声nC都进行复实数转换,各个模型可以转换为:

(2)

(3)

(4)

(5)

其中R(·)表示复矩阵或者向量的实部,I(·)表示复矩阵或者向量的虚部。

之后信号传输可以改写为

y=Hx+n。

(6)

文中的SNR是指每个接收天线的平均信噪比(signal-to-noise ratio, SNR),表达式如下:

(7)

2 算法设计

2.1 MMSE算法信号检测

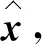
W=(HTH+σ2I2K)-1HT。

(8)

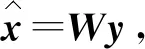
(9)

A表示MMSE滤波矩阵,b表示y的匹配滤波输出。通过式(9)可以发现,检测过程可以看作线性方程组问题。不过需要注意的是,A矩阵直接求逆需要复杂度数量级为O(K3)。

2.2 Barzilai-Borwein迭代算法

Barzilai-Borwein迭代是由Barzilai和Borwein提出的迭代方法,与传统最速下降法使用固定步长相比,该迭代方法式在沿着最速下降方向来选择合适的步长。式(9)可以转换为线性方程组问题:

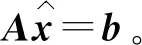
(10)

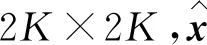
(11)

Barzilai-Borwein迭代的基本形式[15]为

(12)

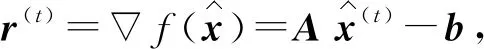
(13)

迭代算法的初始值不影响算法的收敛性,但初始值选取对迭代算法的收敛速度和检测精度有一定影响。一般来说,初始值用零向量时,算法收敛会很慢。为了拥有更快收敛速度,本文算法选取Richardson初值[21]

(14)

2.3 改进修正Barzilai-Borwein迭代算法

修正Barzilai-Borwein算法[17]是Raydan和Svaiter结合Barzilai-Borwein和最速下降法提出的一种非单调下降算法,具体的迭代表达式:

(15)

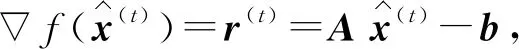
(16)

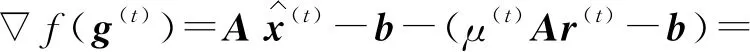
(17)

令h(t)=Ar(t),整理式(15)可得

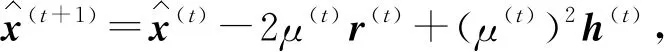
(18)

本文尝试对上式中步长改进变为θμ(t),其中θ∈(0～α),考虑到步长如果太大,会导致算法无法收敛,所以α最大值设定为2,式(7)可改写为

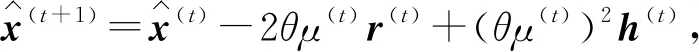
(19)

图2图3为对于不同θ进行仿真对比。

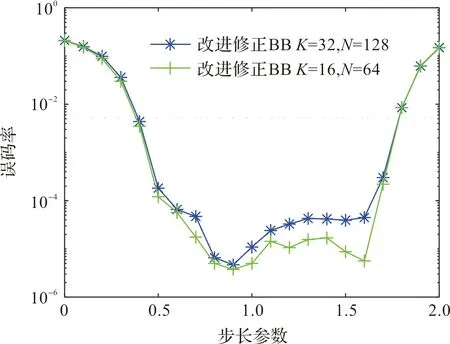
图2 32QAM情况下,不同步长与误码率之间关系

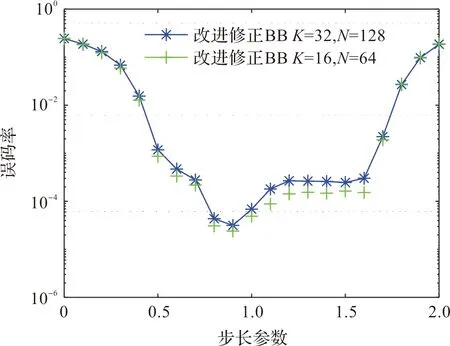
图3 64QAM情况下,不同步长与误码率之间关系

通过图2图3的仿真可以看出,两种情况下,采用步长为0.9倍时,误码率是相对最低的,后续本文算法采用0.9倍步长来进行算法仿真。

结合上文描述,改进修正Barzilai-Borwein算法的流程可以总结如表1。

表1 改进修正Barzilai-Borwein的信号检测算法

3 性能分析

对于大规模MIMO信号检测系统,计算复杂度是衡量检测器性能的重要指标之一。虽然CBB迭代算法比Barzilai-Borwein多出来一项,但其实其中复杂度高的部分h(t)=Ar(t)在求解μ(t-1)过程中已经得到,因此两种算法的复杂度差不多,同时本文在修正CBB算法基础上进行改进,复杂度的增加很少。本文将一次实数乘法的复杂度记为1,不同算法都需要HTH的复杂度为8NK2,HTy的复杂度为4NK。

通过修正Barzilai-Borwein迭代算法的形式,计算各部分的复杂度。

1)初始解的复杂度

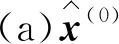
2)修正Barzilai-Borwein迭代复杂度

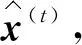
(b)h(t)的复杂度:包括一个2K×2K的矩阵A和一个2K×1的向量r(t),它需要的复杂度为4K2。

(c)θμ(t)的复杂度:包括一个1×2K的向量(r(t))T和一个2K×1的向量r(t),还有一个1×2K的向量(r(t))T和一个2K×1的向量h(t),还有两个常数相乘需要复杂度为1,需要的复杂度为4K。

表2为不同算法复杂度的比较。

表2 不同算法复杂度对比

4 仿真分析

为了验证本文算法的有效性,采用MATLAB程序对算法进行了仿真实验,将其与Barzilai-Borwein算法、CBB算法和MMSE算法进行了对比,采用误码率作为指标来对改进修正Barzilai-Borwein算法性能进行评价。为了更好对比Barzilai-Borwein和本文所提算法,将Barzilai-Borwein算法也采用了Richardson初值进行仿真,各仿真选用的帧数L=20 000;信噪比范围设置在0∶15 dB;信源数据采用randi函数随机生成,天线采用了两种配置32×128和16×64;调制方式采用了32QAM和64QAM两种方式;不过图4的具体参数设置为32×128,调制方式为32QAM;图9的信噪比设置为12 dB,用户天线范围设置为32∶64,基站天线数为128,调制方式为32QAM。

如图4可以发现在低信噪比的情况下,由于噪声对于信号的比重很高,检测算法无法有效区分信号,因此无论迭代的次数如何改变,误码率曲线基本保持不变。对比之下,在信噪比到10 dB时候,误码率曲线开始有下降趋势,并且最终随着迭代次数增加到4时,误码率基本保持到一个稳定值;在信噪比12 dB可以明显发现误码率曲线随着迭代次数增加下降快速,并且在迭代4次时,误码率基本维持在10-6,随着迭代次数提高,误码率还有小的提升,但是相对于提升的复杂度来说,继续进行迭代,并不是一个好的策略。

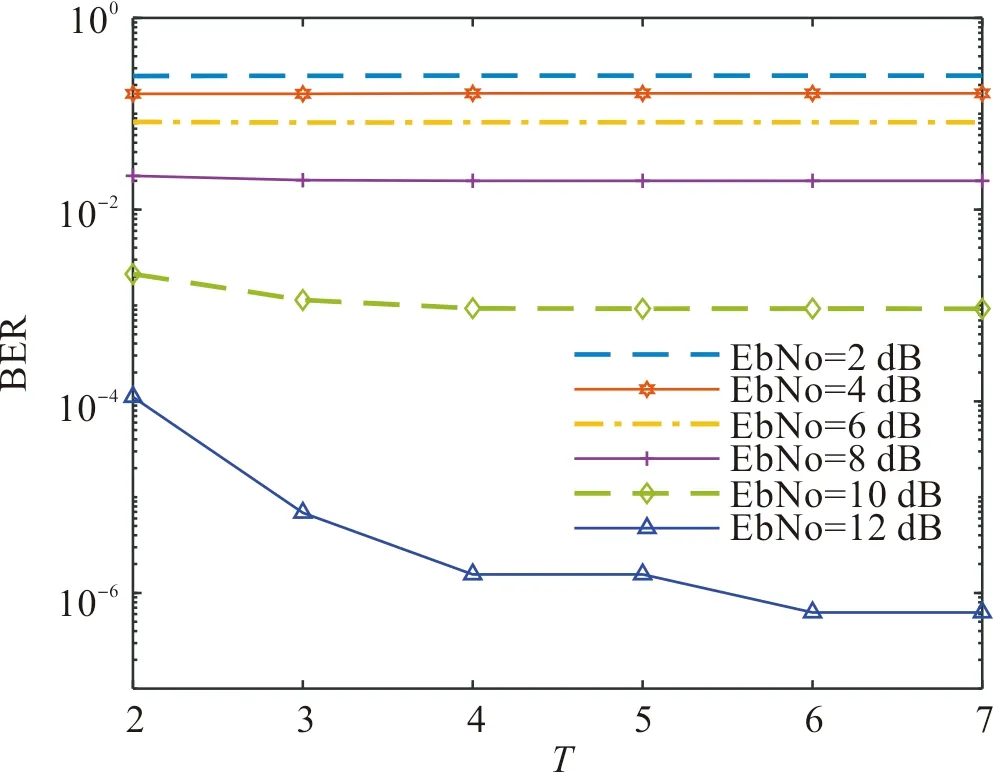
图4 不同迭代次数下,不同信噪比对应的误码率曲线

如图5,表示的是采用32QAM调制方式下32×128天线数情况下不同算法的误码率曲线图。Barzilai-Borwein算法误码率曲线随着迭代次数增加误码率虽然下降速度较快,但是与MMSE算法相比较来说,依然存在差距;CBB算法在迭代3次时,算法的误码率曲线与Barzilai-Borwein算法迭代4次时的曲线基本相同。改进修正Barzilai-Borwein算法的收敛速度明显更快,该算法在迭代3次时已基本接近CBB算法迭代4次曲线,并且迭代4次时已基本接近MMSE检测性能。

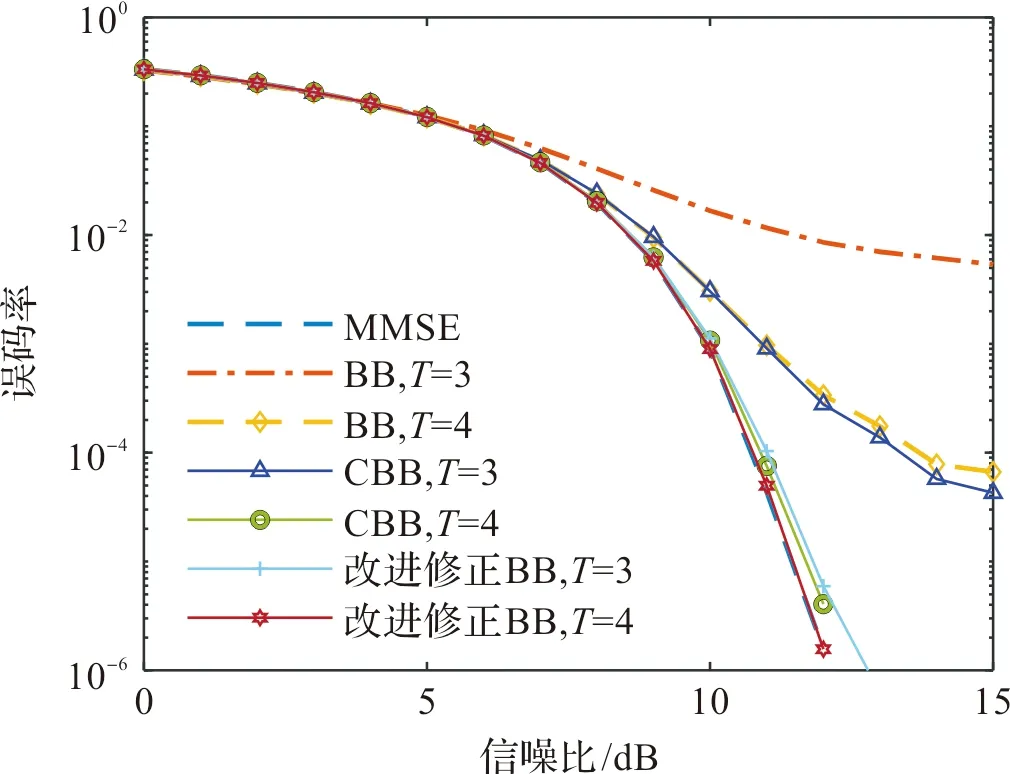
图5 在32QAM和32×128条件下,不同信噪比下误码率

图6表示的是32QAM调制16×64的情况下,不同算法的误码率曲线。Barzilai-Borwein算法在迭代4次时,信噪比在15 dB左右时,误码率才降低到10-4左右;CBB算法,迭代3次时,信噪比在13dB左右误码率已经降到10-4,同样的改进修正Barzilai-Borwein在迭代3次时,13 dB左右误码率就已经低到10-6,并且改进修正Barzilai-Borwein算法在迭代4次误码率曲线已接近MMSE算法。

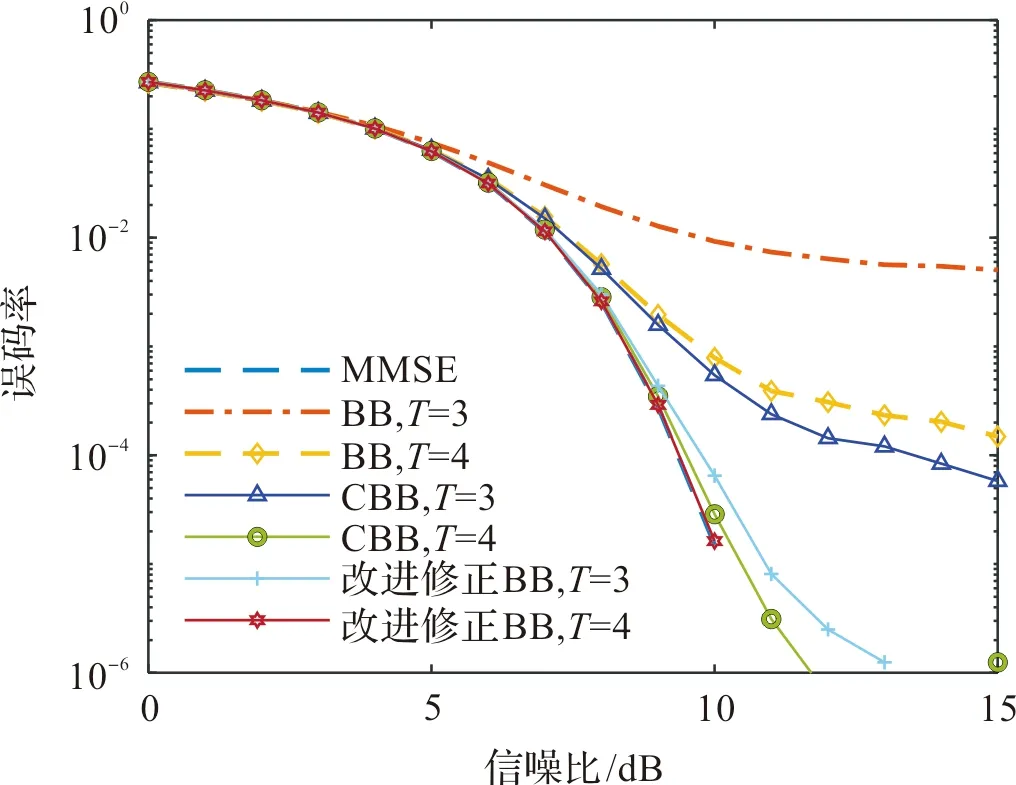
图6 在32QAM和16×64条件下,不同信噪比下误码率

如图7,与图5相比,随着调制方式提高,各个算法误码率曲线降低变缓,通过两图对比,即使调制方式提高,改进修正Barzilai-Borwein算法依然保持自己的优势,在迭代4次时依然与MMSE接近。

图8与图7对比也可以发现,在基站天线数与用户数比值不变时,基站天线数和用户天线数大小变化并不会影响本文所提算法的性能,改进修正Barzilai-Borwein算法依然保持这高收敛,仅需要很少的迭代次数就可以达到MMSE性能。

图7 在64QAM和32×128条件下,不同信噪比下误码率

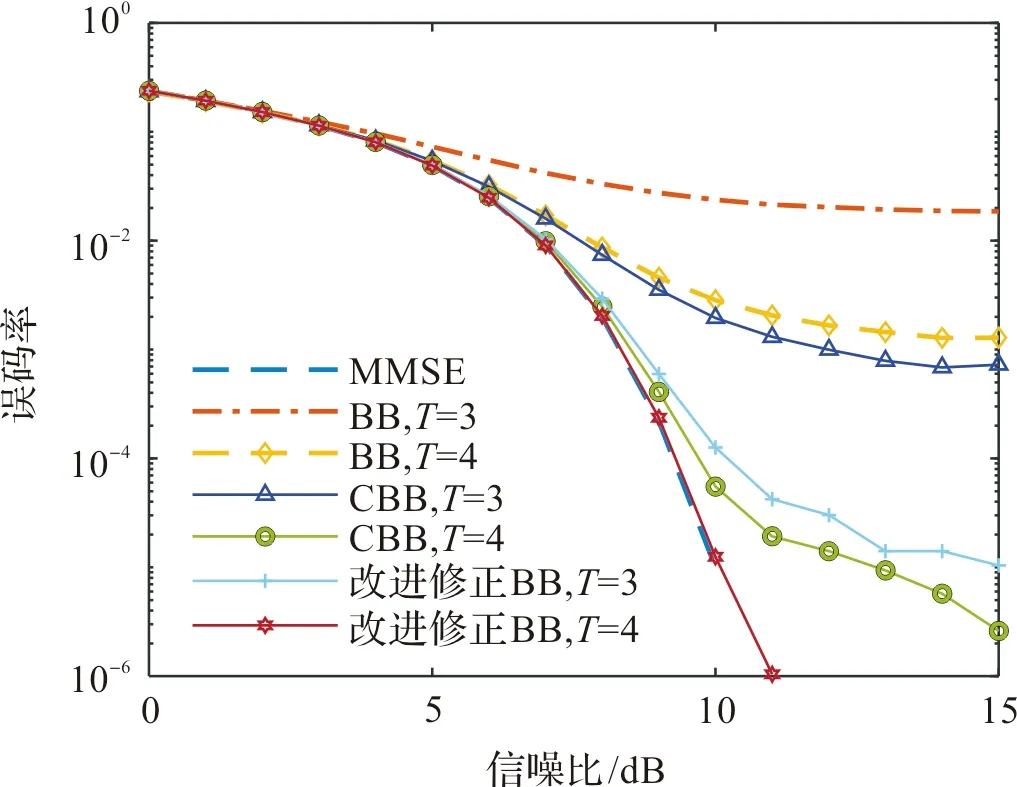
图8 在64QAM和16×64条件下,不同信噪比下误码率

图9是在不同用户数下各算法的误码率曲线图,随着用户数的降低,各算法的误码率都在降低,CBB算法迭代4次与改进修正Barzilai-Borwein的迭代3次误码率曲线基本重合,与此同时也改进修正后的Barzilai-Borwein算法误码率在迭代4次时,虽然在用户数较高的情况下,与MMSE相比较性能稍差一点,但总体依然很接近MMSE性能,并且通过整体可以发现,用户数在32:64变化,本文提出算法整体性能依然优于Barzilai-Borwein和CBB算法。

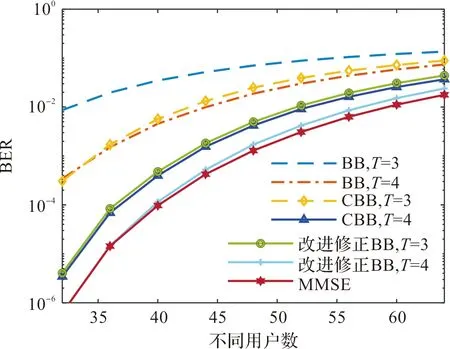
图9 天线数为128,不同用户数对应的误码率曲线

5 结 语

MMSE算法可以实现近似最优的性能,但是由于其实现需要的复杂很高,无法满足实时性要求,在实际场景中无法应用,而改进修正Barzilai-Borwein算法相对MMSE算法复杂度降低了一个数量级,同时在迭代4次时也基本达到MMSE性能。Barzilai-Borwein和CBB算法虽然单次迭代实现复杂度与改进修正Barzilai-Borwein来说相对较低,但是本文提出算法需要更少的迭代次数,就可以基本达到MMSE算法的检测性能,所以在一定程度上,该算法依然有优势。总的来说,该算法可以在检测性能和实现复杂度方面达到平衡。