非饱和渗流模拟中非均匀空间网格的改进方法

朱帅润，何 博，吴礼舟，李绍红，卿毅伟

（1.上海交通大学土木工程系，上海 200240；2.重庆交通大学山区桥梁及隧道工程国家重点实验室，重庆 400074；3.成都理工大学环境与土木工程学院，四川 成都 610059）

非饱和渗流问题广泛存在于众多领域，如地质工程中降雨作用下土质边坡的稳定性分析[1−4]，地下水科学中溶质迁移模拟[5−6]，以及矿业工程中煤层注水和煤层气开采等[7−8]。其中，Richards方程[9]是非饱和渗流数值模拟的基本方程，有效并可靠地数值求解Richards方程对相关领域的科学研究和生产具有十分重要的意义。

Richards方程通常有3种形式，包括压力水头形式、含水率形式和混合形式[10−12]。其中，压力水头形式的Richards方程备受关注。Richards方程的解析解可在一些简化条件下获得[13−14]。如，Parlange 等[15]求解推导了一维Richards方程的复杂级数解以便获得入渗通量；Warrick等[16]假设了一个简单的土水特征曲线并推导出一维Richards方程的解析解。然而，水力传导系数和土水特征曲线在现实中非常复杂，这导致高度非线性的偏微分方程，因此解析解的获得非常困难。因此，在实际条件下Richards方程的求解只能通过数值方法获得[17−20]。

在Richards方程的数值求解中，数值离散方法通常是必要的，常用的空间数值离散方法包括有限差分法[21]（FDM）、有限体积法[22]（FVM）以及有限元法[23]。对于时间离散化，通常采用向后差分法[24]。例如，吴梦喜[25]发展了求解Richards方程具有更好数值稳定性的一般有限元算法。Zambra等[26]构造了在空间和时间上具有很高精确度的有限体积法，用于求解非线性Richards方程。Chávez-Negrete等[24]提出了改进的有限差分法并结合自适应步长的Crank-Nicolson方法用于求解Richards方程。虽然在数值方法上有很多改进，但传统的FDM和FVM都需要非常精细的网格来解析复杂的渗流区域，从而导致更多的计算时间。因此，越来越多的研究关注于非结构网格的改善[27−28]。最近，Deng等[27]利用非正交网格的坐标变换便捷地求解了复杂地形中的饱和-非饱和渗流问题。Chávez-Negrete等[24]采用不规则的三角形网格加密边坡表层，获得了更可靠的数值解。Dolejší等[28]开发了一种各向异性网格自适应技术，这种方法在不损失精度的情况下显著减少了自由度的数量以及计算时间。郑川东等[29]提出一种动态局部自适应空间网格方法用于求解水流水质耦合方程，相对于传统结构均匀网格模型，该方法精度高、效率高，能够自动捕捉计算敏感区域，准确模拟复杂流态和物质的迁移扩散。何金辉等[30]在离散元软件PFC2D基础上，开发了考虑流体动网格的颗粒-流体耦合算法，有助于提高模拟大变形下的一维固结试验等案例的数值精度。此外，一些模拟软件也采用了动态网格划分方法以获得更好的数值结果，如 ANSYS、FLUENT 等[31]。

由此可知，非均匀空间网格的使用在一定程度上可以有效降低计算量，同时也能保证计算精度。但在一些不利数值条件下，比如入渗于初始干燥土壤中，以及分层土上下两层的水力传导系数相差较大时，上述研究的非结构空间网格以及动态网格方法的实现往往较为复杂且不太合适，因此，本文提出采用一种非均匀Chebyshev空间网格改进的FDM数值离散过程，并与传统均匀空间网格获得的数值结果和解析解对比验证。

1 数值求解过程

1.1 控制方程

通常，Richards方程可用于描述多孔介质中非饱和渗流问题，其一维压力水头形式可以表示为[32]：

式中：h——压力水头/m；

t——时间/h；

Kz(h)——相对于z方向的水力传导系数/（m·s−1）；

C(h)——容水度/m−1，C(h)= ∂θ/∂h；

θ——含水率/%。

在非饱和土渗流问题中，本文假设水力传导系数和含水率相对于压力水头的数学关系由下面的指数模型给出[33]：

式中：θr——残余含水率/%；

θs——饱和含水率/%；

Ks——土体的饱和水力传导系数/（m·s−1）；

α——土性相关的模型拟合参数。

1.2 均匀网格法

为了获得式（1）的数值解，传统的有限差分法采用均匀网格法进行数值离散[22]。首先，z轴上的间隔被分为N等分，模拟时间被分为M等分。进而，式（1）的一、二阶空间导数离散采用中心差分格式，时间导数则采用后向差分格式，其有限差分格式为：

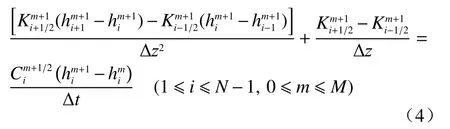
式中：i——沿z轴的离散节点（边界节点除外）；

m——时间节点数；

∆z——离散的均匀空间步长（图1）；

图1 均匀网格和Chebyshev网格的示意图Fig.1 Schematic diagram of uniform grid and Chebyshev grid.

∆t——离散的时间步长。

考虑稳态情况时，其有限差分格式可简化如下：

式中：Ki+1/2、Ki−1/2——相邻节点对应的水力传导系数的调和平均值，可表示为：

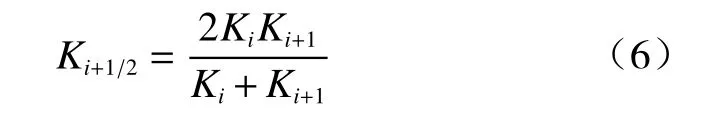
式（4）（5）所构成的线性方程组可进一步写成矩阵形式：

式中：A——(N−1)×(N−1)阶三对角矩阵；

h——(N−1)维列向量；

b——(N−1)维列向量，此处向量b的首尾元素已包含了边界条件。

1.3 改进的Chebyshev网格法

由于非饱和渗流问题中压力水头在边界和土层分界面往往存在较大的变化，因此通常需要一个更精细的网格来进行加密。然而传统的均匀网格在加密过程中，将产生过多的计算网格节点，计算费时甚至仍不够精确。考虑上述情况，提出一种Chebyshev网格坐标[34]：

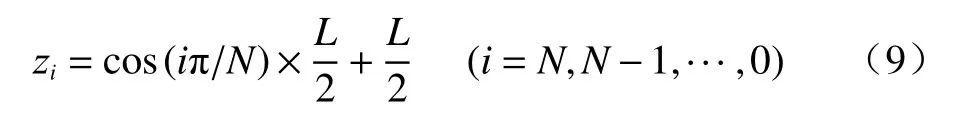
式中：L——土层厚度。

如图1（b）所示，Chebyshev网格节点只会在界面处进行高度加密，很大程度上降低了网格节点数量。结合Chebyshev网格的FDM离散格式可以表达为：

式中：∆zi——Chebyshev网格节点之间的不等间距；

δzi——计算节点处前后Ki+1/2和Ki−1/2之间的不等间距，如图1所示。

式（10）也可以简化为如式（8）的矩阵形式，由于水力传导系数和含水率的非线性关系，通常数值离散后需要采用非线性迭代法对系数矩阵A反复评估并迭代计算。其中，Picard法是比较经典和实用的非线性迭代方法，即：

式中：k——迭代次数。

对于迭代过程，当相对残差满足如下迭代容差时，迭代终止：

式中：ε——迭代容差，在这次研究中设置为10−8[35]。

基于上述Richards方程的Chebyshev网格离散格式，使用MATLAB（版本：R2014a）语言开发了有关非饱和渗流的程序。

2 数值评价

2.1 均质土的非饱和渗流

该案例描述的是均质非饱和土中的一维瞬态非饱和渗流[17]，假设土层厚度L= 10 m，指数模型参数设置为： α= 1×10−4、θs= 0.50、θr=0.11，以及饱和水力传导系数Ks= 2.5×10−8m/s。此外，边界条件可以写为：

假设h0= −105m，该瞬态非饱和流问题的精确解为[36]：

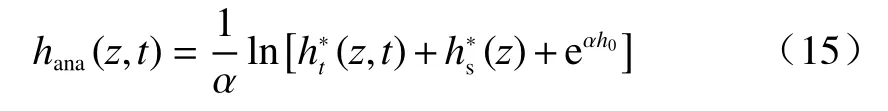
其中，

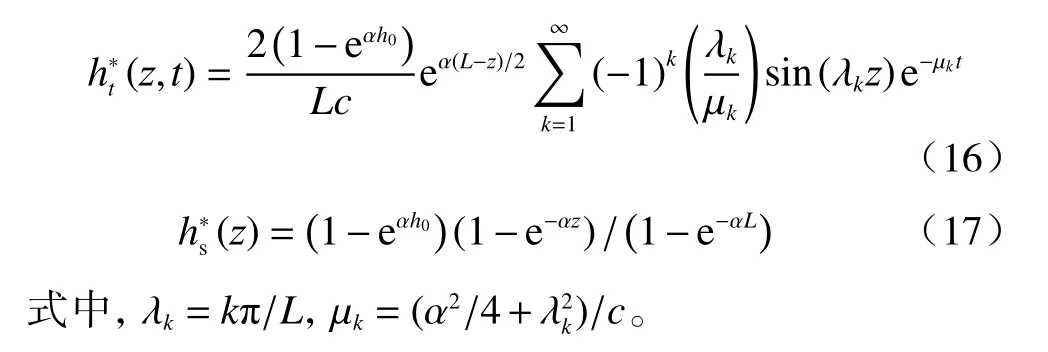
此外，选择3个指标，即均方根误差（RSE），相对误差（RE）和最大相对误差（MRE），验证所提网格方法的计算精度：

式中：hi——模型数值计算值；

3个指标的值越小，表示模型数值计算的精度越高。总模拟时间设置为5 h，节点数分别取为100，150，200，时间步长（ ∆t）分别取为 0.01，0.02，0.04 h。图2（a）显示了当节点数N=100时，不同时间步长下不同网格方法获得的MRE，可以看出Chebyshev网格法获得的MRE范围在0.6%～4.5%之间，随时间t的增加表现为先减小后增大，当t<4 h时，MRE随着 ∆t的减小而减小；而均匀网格法获得MRE范围在1.3%～49%之间，尤其当t>1 h时，MRE随着t的增加而增大，并远远大于Chebyshev网格获得的MRE。图2（b）显示了当时间步长 ∆t=0.01 h时，不同离散网格节点数下不同网格方法获得的MRE，可以发现均匀网格获得MRE随着时间t的增加而增大，当t>1 h时，其误差越来越大；而Chebyshev网格法获得的MRE范围仅在0.3%～2.3%之间，随着时间t的增加表现为开口向上的抛物线，此外，两种方法的MRE随着网格节点数N的增加均有减小的趋势。

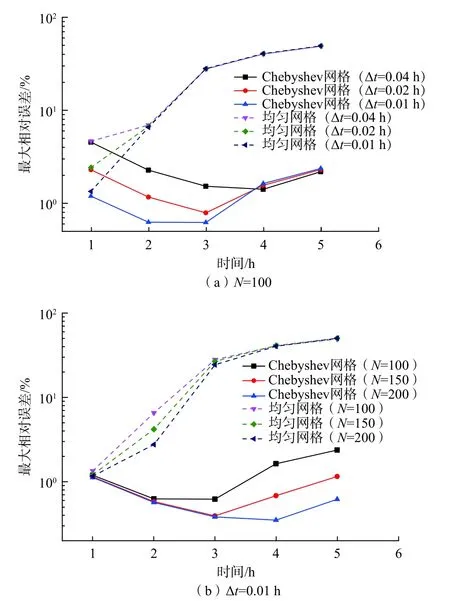
图2 不同数值条件下不同网格方法的最大相对误差的比较Fig.2 Comparison of the maximum relative error of different grid methods under different numerical conditions

如图3所示，在 ∆t=0.01 h和N=200条件下采用两种网格方法获得数值解，并与精确解进行比较。可以发现，均匀网格法获得的数值解与精确解存在较大的偏差，尤其在时间t>2 h后，如图3（a）所示；而Chebyshev网格法获得数值解与精确解十分吻合，随着时间t的增加，相对误差较小，如图图3（b）所示。

图3 不同网格方法下获得的数值解和精确解的比较Fig.3 Comparison of the numerical solutions obtained by different grid methods and exact solutions

正如表1所示，在t=5 h时，可以看到两种方法的RSE和均匀网格的RE均随着N的增加而减小，而Chebyshev网格的RE随着N的增加而增大，但从数值上可以看出Chebyshev网格的RSE与均匀网格法相差近100倍，而RE与均匀网格法相差10倍以上。

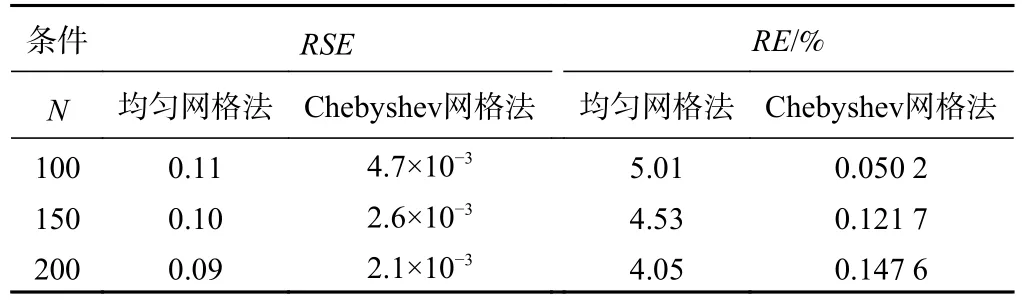
表1 t=5 h时的数值精度Table 1 Numerical accuracy at t=5 h

这个案例说明了提出的Chebyshev网格方法并不因网格节点数的限制而改善精度，也就是说，该方法可以在较少的节点数下获得较高的数值精度，又具有较小的计算开销。

2.2 分层土的非饱和渗流

利用分层土中非饱和稳态流对提出的改进网格方法进行进一步的验证，其数学模型如图4所示。两层土的模型参数设置为θs= 0.35，θr=0.14， α = 8×10−3。此外，土层 1厚度（L1）和土层 2厚度（L2）均设置为5 m，边界条件与上一个案例一致，其中初始条件h0=−103m。对于两层土，Chebyshev网格节点坐标可以定义为：

图4 两层非饱和土的Chebyshev网格Fig.4 Chebyshev grid of two-layer unsaturated soil

式中：N1和N2——土层1和土层2所离散的节点数，本案例中N1和N2均假设为40。

在分层土中，由于不同土壤类型组合的影响，不同的组合对非饱和渗流存在很大影响。正如表2所示，不同土壤的饱和水力传导系数是不同的。为了进一步验证所提网格的适用性，假设土层1的饱和水力传导系数（Ks1）为固定值 10−1m/s，土层 2逐渐从粗砂土转变为细黏土，其水力传导系数（Ks2）从 10−2m/s变化为 10−9m/s（表3）。

表2 饱和土壤的水力传导系数Table 2 Hydraulic conductivity values for saturated soils

表3 工况1至8的水力传导系数Table 3 Hydraulic conductivity for cases 1 to 8

从图5（a）可以看出，均匀网格和Chebyshev网格获得的数值解是近似的，均可以较好模拟出工况2的非饱和渗流规律。图5（b）描述的是工况4的数值结果，土层1、土层2的饱和水力传导系数的比值为104，均匀网格无法精细刻画分界面处的压力水头，而Chebyshev网格获得的数值解却可以较精细地刻画分界面处压力水头的变化。正如图5（c）所示，Chebyshev网格在工况6时也能精细地刻画出分界面处的压力水头变化规律。这个案例进一步说明了所提的Chebyshev网格方法在一些不利入渗条件下尤其在两层土的饱和水力传导系数相差甚大时，均能以较少的网格节点数获得更可靠的数值解。

图5 不同工况下的数值解比较Fig.5 Comparison of numerical solutions for different cases.

2.3 与软件Hydrus-1D的对比

将提出的网格方法与软件Hydrus-1D进行对比以进一步验证改进网格方法的准确性。其中，土水特征曲线（SWCC）采用Van Genuchten模型[37]来描述：

式中：s——基质吸力/kPa，可近似为负孔隙水压力；

Se——有效饱和度，Se=1/[1+(αvs)n]m；

αv、n、m——与土性相关的模型参数，并且m=1 − 1/n。

采用甘肃省天水市的次生黄土进行土柱入渗实验。通过现场入渗过程监测，饱和水力传导系数为1.5×10−7m/s。如图6所示，根据土壤含水率和基质吸力的实测数据，采用Van Genuchte模型拟合得到SWCC，其确定系数R2为0.95。此外，Van Genuchte模型的拟合参数如图6所示。数值模拟中假设模型深度为60 cm，总模拟时间为160 h，初始条件设置为 −260 kPa。在Hydrus-1D模拟中，空间离散采用均匀网格，其步长设置为0.5 cm。基于本文的均匀网格法和Chebyshev改进网格方法，时间步长和离散节点数分别设置为0.1 h和120。

图6 Van Genuchten 模型拟合得到的SWCCFig.6 SWCC fitted by Van Genuchten model.

图7显示了采用Hydrus-1D软件和本文提出方法的数值结果，可以看出提出方法的数值解与软件Hydrus-1D的模拟结果比较吻合，而且Chebyshev网格获得的数值解比均匀网格获得的数值解更接近于Hydrus-1D的数值解。如表4所示，Chebyshev网格相对于Hydrus-1D数值解的RSE、RE和MRE均小于均匀网格的数值，这表明提出的改进网格方法在相同离散网格节点数下更加准确合理。

图7 不同方法下获得的数值解的比较Fig.7 Comparison of the numerical solutions obtained by different methods

表4 数值精度比较Table 4 Comparison of the numerical accuracy

3 结论

（1）非饱和渗流数值求解时，尤其在有限差分法中，数值离散条件的空间步长往往需要较小的步长才能获得可靠的数值解。这往往使得计算费时，甚至在一些不利数值情况下数值精度也并不能得到很大改善。提出的Chebyshev网格方法在保持离散节点数不变的情况下，通过一个余弦函数在两侧界面进行加密，进而再数值求解获得更可靠的数值解。

（2）数值结果表明，在极端干燥的初始条件下，所提Chebyshev网格方法获得的数值解与精确解十分吻合；在两层土中上下土层的水力传导系数相差较大时，Chebyshev网格方法所获数值解也能在较少的节点数下精细刻画出压力水头在分界面处的变化规律，与常规的均匀网格方法相比，该方法可以在较少的节点数下获得较高的数值精度，又具有较小的计算开销。

（3）在分层土中由于界面处水力传导系数的平均化，往往也会使得计算效率下降，本文提出的空间网格方法可以在降低离散节点数层面上提高计算效率。同时，对比软件Hydrus-1D，可以发现提出的方法与Hydrus-1D的数值解是比较吻合的，并且相较于均匀网格方法，提出的Chebyshev网格方法在相同离散网格节点数下是更加准确合理的。