以大概念为引领 同构迭代推动探究
——以《直线与平面垂直的定义、判定》为例

李平香

（1.三明市第二中学，福建 三明 365000；2.福建教育学院数学教育研究所，福建 福州 350001）

涂荣豹教授指出：所谓“探究”，顾名思义就是要“探”要“究”.何为“探”？试探、摸索、探索，不知前方深浅曲折，摸索前进，“摸着石头过河”；何为“究”？深究、追究、穷究，非得弄个明白，搞个水落石出不可，不达目的誓不罢休.［1］“探究”要如何“探”才能预知前方深浅曲折呢？摸着哪些“石头”才能顺利“过河”呢？要“究”什么才能“水落石出”“达到目的”呢？章建跃博士指出：“大概念”对学生学会用数学的方式对事物进行观察、思考、分析以及发现和提出数学问题等都具有“指路明灯”的作用.所谓大概念（big idea）就是对内容及其反映的数学思想和方法的进一步提炼和概括，是对数学对象的定义方式、几何性质指什么、代数性质指什么、函数性质指什么、概率性质指什么等问题的一般性回答，是研究数学对象的方法论［2］.

这一轮课改的显著特征是“强调数学的整体性，以具有整体性的知识单元为载体，从知识的联系性出发进行‘单元—课时’教学设计与开展课堂教学”.［3］“单—课时”整体教学的难点在于如何将核心素养落实到教学中，以“什么”作为统领单元整体教学的具体目标.于是，理论界和实践界都将目光聚焦到大概念，但是，如何把大概念引领下的“单元—课时”教学等“理想课程”“理想观点”落实在“课时”的课堂教学中，这需要一线教师努力提升专业发展水平，提升教学设计能力，增强课堂实践能力，通过大概念揭示教学内容之间的关系，把基于数学整体性的“单元—课时”教学进行积极实践，不断提供有参考价值的实践课例.本文以《直线与平面垂直的定义、判定》为例，谈谈用大概念引领的数学探究的教学.

一、创设情境明确研究对象，进行“单元整体”的探究

问题1：你能从图1、图2 中交警执勤的场景、姿势、动作等现场情境中抽象出直线与平面的位置关系吗？

图1

图2

追问1：你能在教室内找到直线与平面相交的实例吗？

追问2：直线与平面的相交方式有几种？

【设计意图】让学生在交警执勤的场景、姿势、动作的现实情境中，抽象出直线与平面的位置关系，用生活实例直观地认识直线与平面相交的两种方式：垂直交与斜交，获取研究对象，明确“为什么学”.

问题2：“直线与平面垂直”与上一节学习的“直线与平面平行”都是研究两类不同维数空间基本图形的位置关系，根据研究对象的这一共同特点，类比“直线与平面平行”，你认为要具体研究“直线与平面垂直”的哪些内容？按怎样的过程展开研究？采取什么研究方法？

【师生活动】让学生回顾总结直线与平面平行关系的研究内容、研究方法，教师帮助完善.研究内容是直线与平面垂直的定义、判定、性质等；研究过程是沿着“直观感知—操作确认—思辨论证—度量计算”的认知展开；研究方法是“把空间问题转化为平面问题”即“平面化”，这也是学习立体几何问题的基本方法.

【设计意图】根据“直线与平面垂直”是研究两类不同维数空间基本图形的位置关系这一特征，找到与其具有类似结构的“直线与平面平行”一课进行关联思考和整体设计，明确具体要研究“直线与平面垂直”的定义、判定与性质等内容，设计研究思路，寻找研究方法，让学生进一步明确“学什么”“怎么学”，整体规划直线与平面垂直的学习与探究活动.

二、揭示现实生活现象本质，实现“从无到有”的探究

问题3：研究一类数学对象，定义是出发点.那么，该如何对“直线与平面垂直”下定义呢？

追问1：你还能举出生活中直线与平面相交的例子吗？日常生活中，人们是如何刻画直线与平面斜交与垂直交呢？

【师生活动】学生说出了一些实例后，教师展示图3、图4，意在提示学生日常生活中对直线与平面斜交与垂直交的具体刻画.如图3，比萨斜塔是“斜”的，即斜塔向地面的某一面倾斜；如图4，旗杆是“直”的，即“旗杆没有向地面的任何一面倾斜”.进而提炼：生活中对直线与平面斜交的刻画是直线向平面的某一面倾斜，或直线歪向平面的某一面；生活中对直线与平面垂直交的刻画是“不斜”“不歪”，即直线不向平面的任何一面倾斜，或者说直线不歪向平面的任何一面.事实上，一条直线不向平面的任何一面倾斜，则直线与平面垂直，这也是18 世纪法国数学家克莱罗在《几何基础》中对直线与平面垂直的定义.

图3

图4

追问2：“直线与平面垂直”“直线与平面平行”都是研究两类不同维数空间基本图形的特殊位置关系.请回顾“直线与平面平行”的定义，定义中蕴藏的思维方法、思想方法是什么？

【师生活动】学生回顾，教师补充并用课件展示，尤其注意挖掘内隐的思想方法：“降维”“平面化”.

追问3：如图4，如何“数学地”刻画旗杆的“直”呢？

【师生活动】让学生观察阳光下直立于地面的旗杆（图4），随着时间的变化，旗杆影子所在的直线也在不断地变化，但旗杆所在直线与其影子所在直线形成的位置关系中出现确定的垂直关系.进而，提出猜想：“若一条直线垂直于平面，则这条直线垂直于该平面内与这条直线相交的所有直线”.然后，设计试验进行操作确认.

问题4：如图6，在手机手电筒移动光源的照射下，观察直立于桌面的不透明圆柱体水杯AB及它在桌面的影子BC.随着光源的移动变化，影子BC的位置也在不断地变化，观察并检验水杯所在直线AB与其影子BC所在直线是否保持垂直？

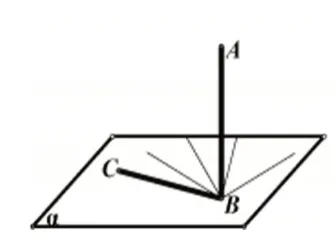
图6

【师生活动】请同学甲用手机手电筒光源照射水杯，同学乙拿着白板笔与直尺画出水杯在桌面上的影子所在的直线，同学丙用直角尺验证垂直.随着光源的移动变化，影子BC的位置也在不断地变化，水杯所在直线AB与其影子BC所在直线总保持垂直.这样就确认了：“若一条直线垂直于平面，则这条直线垂直于该平面内与这条直线相交的所有直线.”

追问：我们知道数学定义是充要条件.接下来，同学们要验证什么？又该如何操作确认呢？

【师生活动】根据充要条件的双向性，学生知道要验证：“若一条直线垂直于平面内与这条直线相交的所有直线，则这条直线垂直于该平面.”依据生活经验“点动成线，线动成面”，教师拿着直角三角板，并将其绕一条直角边旋转，用动作演示并渗透研究“某种位置关系性质”的思想方法，就是探索在这种位置关系下的几何图形组成元素之间以及与其他同类几何图形所形成的位置关系中出现的确定关系（不变性）.具体方法是让“其他几何图形”动起来，看“变化中的不变性”.

问题5：如图7，将PA 绕直角边PO旋转的过程中，什么位置关系没有发生改变？圆锥的轴与底面垂直吗？

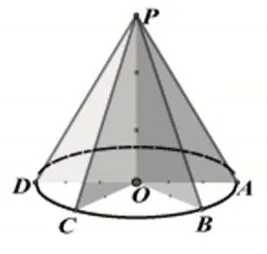
图7

【师生活动】让学生先用直角三角板操作确认，教师再用课件动画演示，观察得到结论：在旋转过程中，直角三角形的两条直角边PO，OA的垂直关系始终没有改变，又圆锥的轴与底面垂直.这样就确认了：“若一条直线垂直于平面上与该直线相交的所有直线，则该直线与平面垂直.”

追问1：你能尝试给直线与平面垂直下定义吗？

【师生活动】通过上面的操作确认，学生能抽象概括直线与平面垂直的定义：“若一条直线垂直于平面上与该直线相交的所有直线，则该直线与平面垂直.”事实上，这也是欧几里得《几何原本》中线面垂直的定义.学生进一步会想到：对于平面上不过点B的任意一条直线也与该直线垂直吗？答案是肯定的，因为对于平面上不过点B的任意一条直线B′C′，总能在平面上找到过点B的一条直线与之平行（图8），再根据异面直线垂直的定义可知AB⊥B′C′.因此，AB垂直于平面内的任意一条直线.进而，完善直线与平面垂直的定义：若一条直线垂直于平面内的任何一条直线，则直线垂直于平面.

图8

追问2：如何画图表示直线与平面垂直？又如何用符号表示？

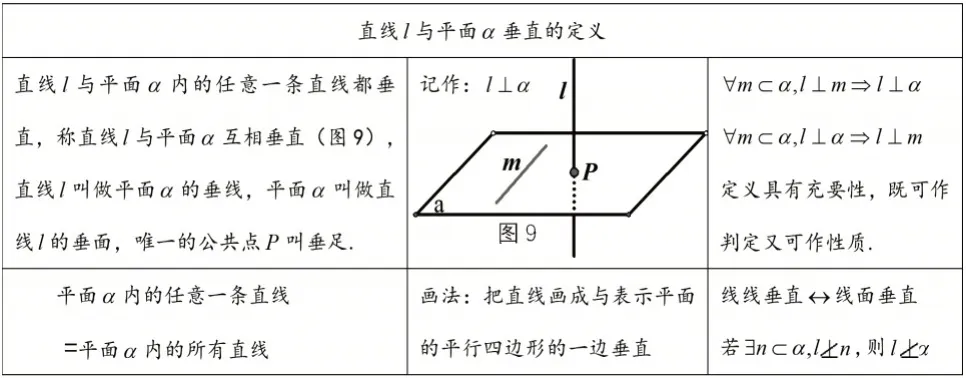
【师生活动】学生自由发言，并相互补充，教师在关键点处进行点评.

追问3：请回顾总结直线与平面垂直定义的探究过程.

【师生活动】学生回顾，教师补充并用流程图展示外显的探究历程、内隐的思维、思想、方法.

【设计意图】用“比萨斜塔”的“斜”衬托“旗杆”的“直”，用“斜”的对立面——“不斜”“不歪”来刻画直；用“降维”“平面化”，以及让组成平面的基本元素——直线“动”起来，观察“变化中的不变性”等数学的方式方法研究“直”，经历“从无到有”的探究；浓缩直线与平面垂直定义发展的历史过程，像专家一样地思考，让学生了解如何定义基本图形的位置关系？定义一种位置关系要完成哪几件事情.［1］

三、构建判定定理的发现模式，呈现“从有到有”的探究

问题6：用定义来判定直线与平面垂直方便吗？“判定”要研究的问题是什么？发现判定定理的思想方法是什么？

【师生活动】学生容易感知：用定义可以判断，但很难验证一条直线与一个平面内的所有直线都垂直.那么，寻找能判定直线与平面垂直的“更好用”“更简便”的方法就很有必要.教师再引导学生分析：“判定”要研究的问题是寻找使直线与平面垂直成立的充分条件，发现判定定理的思想方法是从定义出发探究使“直线与平面垂直”所需要的“最少条件”.

追问1：请观察实物模型：教室内相邻墙面的柱子与地面的关系（图10）；翻开一本书立在桌面，书脊AB与桌面的关系（图11）；直立的落地衣架杆与地面的关系（图12）.从这些实物模型中直观感知，猜想要满足“什么条件”，才能使直线与平面垂直.

图10

图11

图12

【师生活动】学生从实物直观得到充分感知，自然会提出猜想：如果一条直线与平面内的两条相交直线垂直，则这条直线垂直于平面.

追问2：如何设计试验进行操作确认呢？请同学们用桌面上准备好的3 张全等的硬卡纸三角形纸片ABC折纸确认.过△ABC的顶点A翻折纸片，得到折痕AD，将翻折后的纸片竖起来放置在桌面上（BD,BC与桌面接触）.（1）折痕AD与桌面垂直吗？（2）如何翻折才能使折痕AD与桌面垂直？为什么？（3）与桌面垂直的折痕AD能折出几条？你能合理解释吗？

【师生活动】让学生带着问题动手折纸确认，独立思考后，再进行自由发言.得出结论：折痕AD不一定与桌面垂直（图15）；当且仅当沿着底边BC的高线折起，才能使折痕AD与桌面垂直，而且与桌面垂直的折痕AD有且只能折一条（图16）；因为在同一平面内，过一点有且只有一条直线与已知直线垂直（图14），通过折纸试验，还操作确认了这一结论可以推广到空间，即过一点垂直与已知平面的直线有且只有一条.教师进一步引导学生定义垂线段、点到平面的距离（图17）.

图17

追问3：通过上述操作确认，你能得出直线与平面垂直的判定方法吗？联系基本事实中确定一个平面的方法，你能给自己得出的判定方法一个合理的解释吗？

【师生活动】学生独立思考，归纳判定方法，即“一条直线与平面内的两条相交直线垂直，那么直线与该平面垂直”，再联想到基本事实的推论2，平面α可以看成是由两条相交直线DB,DC所唯一确定的平面.所以，当直线AD垂直与这两条相交直线时，就能保证直线AD与平面α内所有直线都垂直.学生自然也会想到：两条相交直线可以确定一个平面，两条平行线也可以确定一个平面，继续追问.

追问4：能把“两条相交直线”改为“两条平行线”吗？你能从向量的角度解释原因吗？如果改为“无数条直线”呢？

【师生活动】请学生用直角三角板进行实物直观演示（如图18、图19），采用“反例证伪法”很快能判断改为“两条平行线”“无数条直线”都不行.教师再引导学生从向量的角度进行解释，因为“两条相交直线确定一个平面”与“平面内两个不共线向量构成一个基底”是等效的.如图16，平面α可以看成是直线DB,DC确定的平面，因为不共线，平面α也可以看成满足的点P的集合；而当两条直线平行时，这两条直线的方向向量也平行，两个平行向量不能构成基底，因为位置关系归根到底是“方向的关系”，平行线的方向一致，所以，平行关系具有传递性，与方向相关的问题中，平行线与一条直线等效［4］.因此，只增加直线的“数量”不行，关键要增加“方向”.

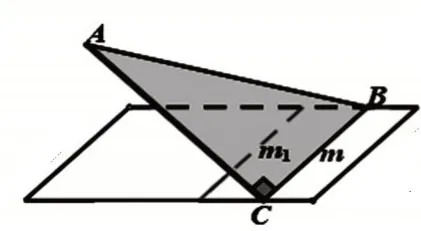
图18

图19

追问5：请用文字、图形、符号三种语言表示直线与平面垂直的判定定理.

【师生活动】学生自由发言，教师补充并提炼注意点.

【设计意图】让学生感知研究“判定”的必要性，明确“判定”要研究的问题是寻找使直线与平面垂直的充分条件，发现判定定理的思想方法是从定义出发探究垂直关系所需要的“最少条件”，引导学生“回到定义去”，在“定义”的基础上，去掉“冗余条件”，探究直线与平面垂直所需要的“最少条件”.让学生“往回找根”“回到原始而不失重要的地方去”“回到基本事实去”［4］，对直线与平面垂直的判定进行“从有到有”的探究，经历“化繁为简”“以简驭繁”的研究问题的一般思路.

四、鼓励学生动手实践求证，引导“从有到富有”的探究

问题7：如图21，如何验证门轴与地面垂直？与门轴平行的另一条边与地面垂直吗？由此，你可以得出什么猜想？请证明你的猜想.

图21

【师生活动】让学生想到通过转动门即可根据线面垂直的判定定理证明门轴与地面垂直.进而，引导学生思考：既然门轴与地面垂直，那么，与门轴平行的另一条门的边框所在的直线也与地面垂直，从而提出猜想：如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面.

证明：如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面.

【师生活动】请学生先画出图形（如图22），再用符号语言表示已知、求证，引导学生寻找证明思路要“由已知想性质，由求证想判定”，沟通已知的条件和求证的结论，本题可以用判定定理证明（如图23），也可以用定义证明（如图24），再请学生规范书写解题过程.

图22

图23

图24

学生提问：如图21，注意到两边的门框所在直线与地面都垂直，两边的门框又互相平行.所以，提出猜想：垂直与同一平面的两条直线平行.

【师生活动】引导学生先分析上面猜想的研究起点是以a⊥α,b⊥α为大前提，研究目标是直线a,b具有怎样确定的位置关系，这是研究直线与平面垂直的性质问题，也是下一节要学习的内容.教学中要让学生明确什么是性质？什么是判定？什么是数学定义？以直线与平面垂直位置关系为例，判定要研究的问题是：探究已知的直线以及与平面有关的直线、平面要具备什么样的位置关系时，该直线才与平面垂直；其性质要研究的问题是：探究在已知直线与平面垂直的情况下，与之有关的直线和平面具有什么样确定的位置关系；定义是界定一类对象的共同特征，这些特征是这类对象的最基本性质.［5］

【设计意图】让学生准确分析已知求证、精确作图、规范表达，体会空间平行与垂直之间的内在联系以及相互转化，经历“从有到富有”的探究活动，“富有”不仅仅是“数量”的丰富，还指“研究视角”的丰富.平行与垂直是整个定量几何的基础所在，所以，不论是研究平行还是垂直，都要既从平行又从垂直的视角进行研究.同时，《普通高中数学课程标准（2017 版2020 年修订）》第一次对理解三种条件与性质、判定和数学定义之间的关系提出了具体的教学要求.尽管学生在平面几何的学习中学过许多数学定义、判定、性质，但学生对数学定义、判定、性质到底要研究什么还是“不甚了了”，始终“朦朦胧胧”；通过上一节“空间直线、平面的平行”这一单元学习，学生已经对数学定义、判定、性质与三种条件的关系“似有所悟”.这里，再直观、明确地呈现并加以对比，能帮助学生从“似有所悟”开始走向“明朗清晰”.

本节课对直线与平面垂直的定义与判定的教学经历了“获取对象，整体探究”“从无到有”“从有到有”“从有到富有”等探究活动.在“抽象数学对象-探索数学性质—构建知识体系”等大概念的引领下，先从现实场景中获取研究对象，再根据研究对象的特征（两类不同维数空间基本图形的特殊位置关系），规划研究内容、寻找研究方法、设计研究思路，进行单元整体探究，让学生明白“为什么学”“学什么”“怎么学”，构建先行组织者，形成“导游图”，确保在课时探究中能始终保持正确的学习路径和明确的学习方向；在“几何元素之间的确定关系就是性质”等一般观念的引领下，根据研究“某种位置关系性质”的思想方法，就是让组成平面的基本元素——直线“动”起来，观察“变化中的不变性”，引导学生用数学的眼光观察“直”，用数学的思维分析“直”，用数学的语言表达“直”，经历“现象描述—本质刻画—精致完善”的抽象概括定义的过程，对定义进行“从无到有”的探究；在“判定就是从定义出发探究垂直关系所需要的‘最少条件’”等一般观念的引领下，让学生“回到定义去”，“化繁为简”“以简驭繁”，在“定义”的基础上，去掉“冗余条件”，“往回找根”“回到原始而不失重要的地方去”“回到基本事实去”［4］，对判定进行“从有到有”的探究；在“判定是什么、性质是什么、定义是什么”等一般观念的引领下，让学生体会空间平行与垂直之间的内在联系以及相互转化，对平行与垂直的关系进行“从有到富有”的探究，“富有”不仅仅是“数量”的丰富，还指“研究视角”的丰富.另一方面，在大概念的引领下，本节课的探究活动都沿着“直观感知—操作确认—思辨论证”的认知过程展开，在连续地、一脉相承地、同构迭代的探究活动中，让学生有了“发现事物的眼光”“洞察本质的智慧”“析解问题的方法”，能自觉地运用“大概念”指导数学学习与探究活动，实现从“知其然”到“知其所以然”再到“何由以知其所以然”的跨越.［6］