基于分类的几何和图形教学实践

蒋开林

【摘 要】在几何和图形的学习中，分类思想可以让学生的探究活动更加有效、思维路径更加清晰、认知网络更加通畅。本文聚焦分类的过程、知识的梳理和问题的解决，借助分类，辨析概念内涵、连通认知网络和架构思维路径，从而提高学生解决问题的能力，发展学生的空间观念，促进学生深度学习。

【关键词】深度学习 分类思想 空间观念

分类思想是数学学习的重要思想方法之一，学会分类有助于学习新的数学知识，有助于分析和解决新的数学问题。尤其在几何和图形领域中，借助分类思想，能促进学生辨析概念内涵，引发学生进行有序思考，从而培养学生的批判性思维，有效发展学生的空间观念。

一、觅起点，辨析概念内涵

数学学习的有效发生，离不开教师对学生的学习起点进行分析和预设。基于分类的几何和图形教学也往往需要从学生的认知起点出发，激发指向概念内涵的分类活动，规避无效或低效的分类任务，尽可能地提高教与学的质量。

（一）明确分类依据，感知概念内涵

在皮亚杰的认知发展理论中，学习分为同化和顺应。小学阶段的数学学习，大部分采用同化，把新知融入已有的图式和认知体系中，发散概念。当新知无法在已有的认知体系中找到呼应的节点时，需要通过顺应，重新建构新图式。对于空间领域的概念学习，由于学生已具有一定的生活经验和认知基础，通过正向的迁移学习，能够轻松掌握新知，但是在实践教学过程中，对于很多看似简单的问题，学生却难以正确地分析和解决。同化的思维惯性，让教师和学生失去对同化学习的警惕和忽视。因此，在新概念的形成过程中，教师应该让学生在充分感知概念的外延的基础上，明确分类依据，通过不断地辨析和比较，明晰概念的内涵和本质的区别，发展批判性思维。

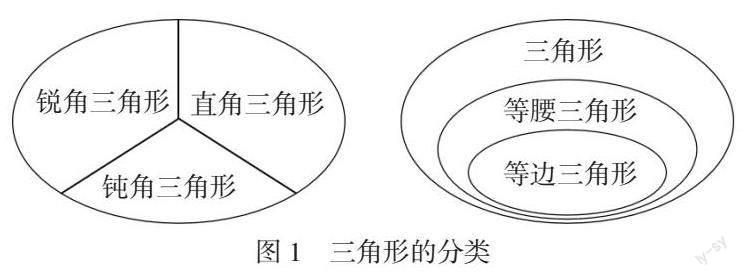
如在三角形的分类中，学生了解了三角形的概念，接觸过各种不同的三角形，那么对三角形进行分类应该不是一个很困难的任务。但是，如果放手让学生自己对三角形进行分类，课堂上会出现各种分类方法，看似在“热闹”的学习中，学生的思维非常活跃。如果仔细去琢磨，太多的分类方法，反而对学生进行正确的分类产生负向迁移。因此，在分类前提醒三角形的特征主要是有关角和边，引导学生从角或边出发进行分类，规避“长相”“是否常见”等低效分类。在学生构建出两类分类后（见图1），教师还应该让学生进一步思考如何把这两种分类进行呼应，如在按角分类的关系图中，等腰三角形、等边三角形可能出现在哪里？教师在对三角形进行分类、辨析和呼应的过程中，加强学生对三角形的认知，培养学生的批判性思维。

（二）明晰分类标准，感悟本质属性

在几何和图形领域的学习中，如果仅仅从丰富、精致的学习素材中“习得”概念，这样的学习活动难以让学生真正感知概念的本质属性。有效的概念学习，应该基于学生的已有认知，让学生探析原有的认知和新知之间的契合点，在认知冲突中进行对比、辨析、想象和抽象，明晰分类标准，从而感悟其本质属性。

如在学习“垂直与平行”时，如果先让学生通过自学找到平行的概念，再从概念出发，通过辨析几组直线的位置关系，从而内化概念，通过“习得—应用—感悟”的学习路径，进行顺向的探究活动，这样，学生的学习相对比较“顺利”，学生出错的概率也比较低，“先学后教”的学习模式也契合以生为本的教学理念。但这样给学生铺好学习坦途的教学，往往让学生感觉概念学习轻而易举，从而导致课中学习轻松愉悦，课后练习错误频出的状况。因此，教师不妨让学生先画出两条直线，对几组直线进行位置关系的分类活动。在教学实践中，我们不难发现，学生对于可明确看出相交和平行的两种情况没有异议。那么，教师就可以聚焦看似不相交的几组直线，让学生通过讨论交流，从直线无限延长的本质属性出发，在操作、想象和辩论中，让分类的标准更加明晰，凸显概念的本质属性，从对现象的分类到本质属性的辨析、抽象和概括，借助分类，使学生对直线的位置关系的认知结构更加清晰。教师还可以进一步进行分类，让学生思考在一组平行线中，再增加一条直线，它们的位置关系又可以分成几类，从而促进学生的深度学习。

二、重梳理，连通认知网络

学生的深度学习，需要对知识点的理解和应用，更需要对知识点进行梳理。通过学习活动和任务驱动，学生在分类梳理的过程中，连通相关的知识点，形成脉络清晰、系统有序的认知网络。

（一）以数衬形，融通知识脉络

在数与计算的学习中，我们常常借助形的支撑，让算理更加形象生动，促进算法和算理的有效融合。而在几何和图形的学习中，我们有时也同样需要借助数的特征，来沟通图形之间的联系，通过分类梳理，在感知序的基础上，把图形融入整个体系中，让整个知识脉络更加清晰。

如在学习“角的分类”时，学生通过拼角和拆角的操作过程，对形成的学习素材进行分类，从而沟通周角、平角、钝角、直角和锐角之间的联系；在用直角拼的过程中，进一步巩固周角、平角和直角之间的倍数关系；在用三角板拼角后，按照角的大小，对所拼得的角进行分类，并按照从大到小排列，再对这些角的度数进一步进行观察，发现用三角板拼出的角都是15°的倍数。这无疑又让学生进一步探究其缘由：三角板的角分别是15°的2倍、3倍、4倍和6倍，因此拼出的都是15°的倍数，也就是说，把角的度数除以15，如果有余数，那么便无法用三角板中的角拼出。有序的排列也能进一步促进学生对角的大小的感知，对学生估测角的大小也有一定的参照依据。学生从生成的素材出发，在分类整理中，找到数与形之间的联系，把各类角融入整个学习活动中，并从中提炼出判断的标准，再提出问题解决的策略。

学生在拆角的过程中，也应该有分类的意识，如把一个钝角拆成两个角有很多种可能，但是把这些可能进行分类的话，可分为三类：钝角=钝角+锐角，钝角=直角+锐角，钝角=锐角+锐角。相对于大小确定的直角、平角和周角，钝角和锐角具有一定的区间范围。在拼角和拆角的任务驱动下，学生通过不断的分类、辨析比较，沟通了这些角之间的联系，感知钝角和锐角所对应的大小范围，让形成的认知网络更加稳固，知识点之间的联系更加通畅。

（二）思维导图，外显认知网络

图形与几何的整理复习，离不开学习素材，而好的学习素材往往来自学生的生成。因此，教师应设计一个好的学习任务，以驱动学生生成素材。学生通过重组素材，在分类梳理中，对认知结构进行解构和重构，连通更多的认知节点，在对比沟通中，让认知网络在原有的基础上生长和拓展。

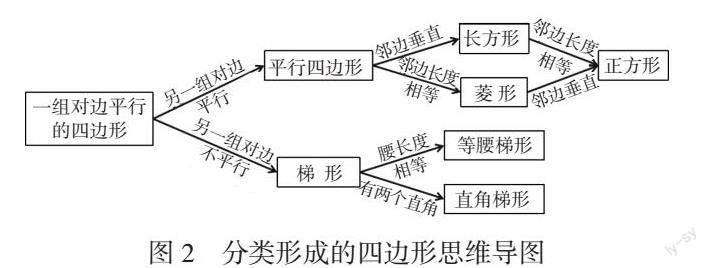
如在对四边形进行分类整理时，教师可以让学生在一组平行线上再增加两条直线，可以围成四边形，借助围成的四边形素材，让学生进行分类，并说明分类的理由，在分类梳理的过程中，唤醒学生对各类四边形的特征认知。（见图2）

随着分类的不断推进，四边形的思维导图也不断得到完善。有了思维导图的支撑，学生对四边形的特征以及它们之间的联系有更加直观、清晰的认识。

三、寻策略，架构思维路径

在解决关于几何和图形的问题中，一旦遇到新的情境或者相对复杂的问题，学生往往手足无措、毫无头绪。这些问题的解决，需要循序渐进的过程。学生应该根据规则进行大胆尝试，积累一定的活动经验，在“操作尝试—分类辨析—提炼策略—应用策略”中，架构解决问题的思维路径。

（一）探析解决策略，促进有序思考

分类思想，不管在生活中还是在今后的学习和工作中，都极具价值。它能让学生用数学的眼光观察世界，用数学的思维思考世界，把具象的感知转化为理性的思索，有助于学生分析问题和解决问题，激发学生的空间想象力。

如数学游戏“小熊戳蛋糕”，游戏刚开始时，教师出示“2×2×2”的正方体蛋糕，可以引导：如果让你戳，可以怎么戳？根据戳的方向，一般来说可以分为6种（从前往后戳、从左往右戳、从上往下戳、从后往前戳、从右往左戳和从下往上戳）和3种（前后戳、左右戳和上下戳），让学生辨析感知：从前往后戳和从后往前戳在解决一共戳中蛋糕的数量时是相同的，在有关空间的问题中，相对的两种可以合二为一。解决“一共戳中几块蛋糕”的策略分为两类：一类是先按上下、前后和左右各戳中几块，再找出重复多算了几次，上下戳中的块数+前后戳中的块数+左右戳中的块数-重复多算的次数=总数，也就是用分类的策略解决；另一类是分别按每层各戳中几块，然后逐层累加，也就是用分层的策略解决。教师在学生感知到这两种策略后，要留足时间让学生去思考辨析这两种策略的优缺点。

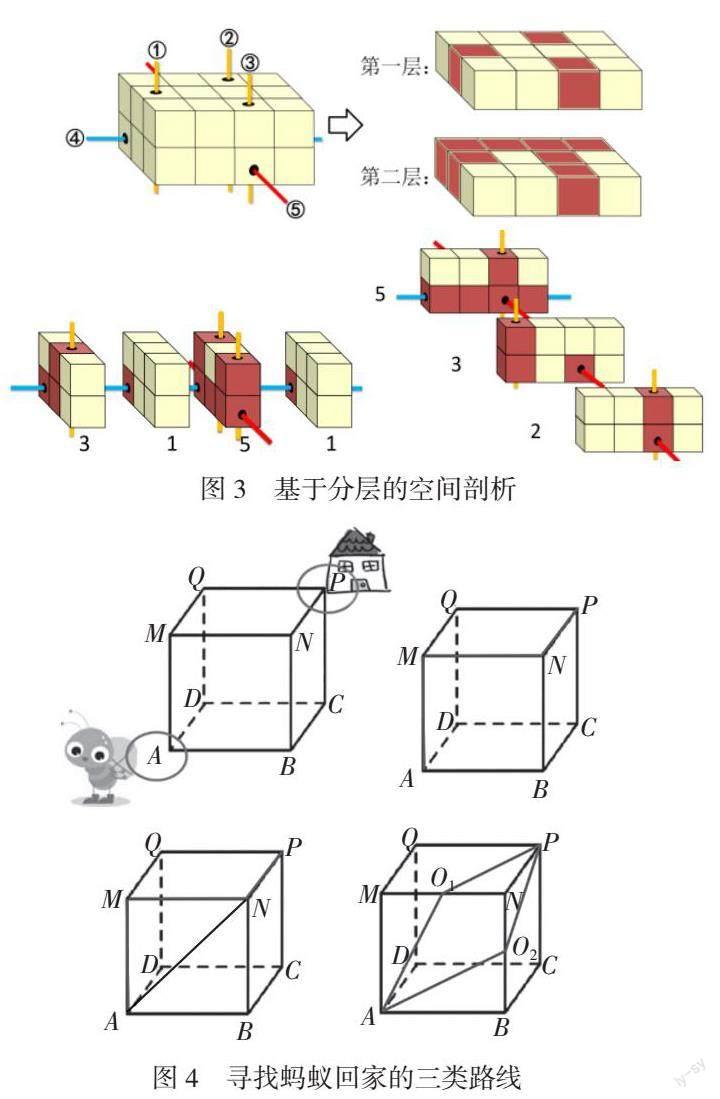
分类的思想，不仅在于让学生用分类的方法去分析问题和解决问题，还在于让学生感受到分类是基于分类标准进行的，不同的分类具有不同的解决问题的路径。学生不仅要学会分类，还要对不同分类进行比较、辨别和选择。分类的策略容易想象，而分层的策略能避免重复带来的干扰，两种策略各有利弊，可以相互补充、相互验证。分层的策略又可以按照不同的方向分为三类：上下分层、左右分层和前后分层（见图3）。对于这三类的感知，其目的在于感知解决三维空间问题的思维路径，进一步提升空间想象能力。

（二）建构分类模型，明晰思维路径

空间相关问题的解决，最大的困难在于模型的感知和建构。当学生无法自行探究出解决的思维路径时，教师不妨让学生进行分类，从而探析解决问题的模型。如果学生建构出有效的解决模型，这将促进学生全面地思考问题，而且，学生在求解的过程中也能“求全”。

如在“寻找蚂蚁回家的最短路线”的游戏中（见图4），蚂蚁从A点出发沿着正方体的表面达到P点，学生根据规则形成很多的路线。我们可以对这些路线进行分类，沿着棱的组合路线（与A点相连的棱有AM、AB和AD三条，如从AM出发，有AM—MQ—QP和AM—MN—NP两条，從AB出发，有AB—BN—NP和AB—BC—CP两条，从AD出发同样也有两条）共6条；沿着对角线和棱的组合路线（先对角线后棱，如AN—NP、AQ—QP和AC—CP，先棱后对角线，如AM—MP、AB—BP和AD—DP）共6条。

把路线进行分类后，学生的思维路径更加清晰，思考也更加全面。对这两类路线进行对比，我们发现对角线和棱的组合路线相对短一些。那么，有没有更短的路线呢？教师引发学生思考：对角线比两条棱长的和要短，也就是说，在平面内两点之间线段最短，如果把这个正方体展开，能否找到一条能够直接连接A点和P点的线段呢？通过正方体的展开图，教师把立体空间的问题转化为平面两点间的距离问题。学生最终得到寻找最短路径的策略：从棱上找中点，中点分别与A点和P点相连，如在棱MN上找中点O1，再连接AO1和PO1，得到的就是最短的路径。像这样的最短路径一共有几条呢？要想找到全部的最短路径，学生就需要对这些路径进行辨析和分类：与A点相连的面有3个，其中在前面可以找到两条），左面和下面也各有2条，一共有6条最短路径。寻找最短路径的过程，离不开学生的空间想象和有序思考。

空间想象和有序思考是解决复杂问题的关键所在。如果思维是混乱的，没有进行有序的思考，是难以正确解决问题的。只有在有序思考的前提下，学生才能正确地分析问题和解决问题，才能有效培养空间观念，发展空间想象力。

大部分的学习和研究都离不开对分类思想的应用，教师要在分类操作中寻找学生的学习起点，在分类对比中辨析概念的本质属性，在分类梳理中连通知识的来龙去脉，在分类思考中提炼问题的解决策略。在图形和几何的教学中，分类是一种有效的、普适的学习方式，能促进认知网络在活动中得到形成、完善和生长，助推学生进行深度学习，进一步发展学生的空间观念。