核心素养视角下的开放式圆锥曲线问题的研究

石义娜　丁红云　夏小刚

［摘  要］ 文章基于核心素养对一道典型的开放式圆锥曲线问题进行多角度思考、多层次探索、多方面推广，主要途径是运用一题多解、问题抽象、类比推广使数学核心素养在知识理解中落脚、在知识迁移中生长、在知识创新中发展.

［关键词］ 核心素养；圆锥曲线；问题研究

《普通高中数学课程标准（2017年版2020年修订）》（简称《课标》）提出的六大数学核心素养［1］，为中国基础教育数学学科的研究与实践指明了方向［2］. 圆锥曲线蕴含着丰富的数学思想和方法，涉及多种核心素养的考查，对学科核心素养的培育起着至关重要的作用. 不少研究显示，师生均认为圆锥曲线内容“理解难、计算繁”，很重要但难学又难教［3］；多数师生认为圆锥曲线内容极为重要在于它在高考中的地位，而不是圆锥曲线本身的教学价值，难学难教关键在于知识本质未厘清，即未建构起内在联系. 在现今教学中，强调多讲题多练题，一味地进行解题训练，注重解题技巧的传授［4］，过于重视解题而忽视对数学知识特别是核心概念的真正理解，使学生难以综合运用知识解决问题，导致解题能力下降的情况屡见不鲜. 此外，多数学生存在“就题论题”“唯分是从”的价值取向，仅重视解答是否正确、能否得分，对知识的理解十分片面，缺乏深入思考的意识，往往还没有真正理解题目内涵及解题模型便将其丢弃. 基于此，文章寄托于一道开放式圆锥曲线问题的多角度思考、多层次探索和多方面推广，注重解题模型的构建，提出更具一般性的问题，进而延伸到一般性结论的教学策略，揭示圆锥曲线的内在联系，体现其教学价值；并以数学核心素养的水平划分为依据，评价核心素养在问题教学过程中的达成情况，在圆锥曲线问题教学研究中逐步揭示核心素养如何落地、生根、发展.

开放式问题的价值及思考

开放式问题是时代发展的产物，它的方法不唯一、答案多样化，能够发展学生的创造思维. 培养学生的创新精神［5］，而高考题是实现课程目标的重要载体之一［6］，是基于学科知识的树人、育人体系之一. 因此，本文选择高考中的一道具有研究价值和教学价值的开放式圆锥曲线问题，即2019年全国高考Ⅲ卷（理科数学）中的压轴题进行讲述. 该题主要考查直线与圆锥曲线的位置关系，将方程、抛物线、切线等知识有机结合，富有思维训练价值，是一道兼具探究性和创新性的开放式问题，考查学生的数学抽象、逻辑推理、数学运算、直观想象等核心素养. 该题的具体内容（第（1）问）如下：

已知曲线C：y=x2/2，D为直线y=-（1/2）上的动点，过D作C的两条切线，切点分别为A，B. 证明：直线AB过定点.

核心素养视角下的开放式问题的研究

在核心素养的视角下，对开放式圓锥曲线问题进行多角度、多层次、多方面的探究是实现“以人为本”理念的现实需求，也是将核心素养融入解题教学的重要尝试. 如何使其落地、生根、发展？前提是理解落地、生根、发展的含义. “落地”指（物体）落在地上，落脚点指目的地，目的地与出发点相对［7］，教学中素养落地和落脚指基本达到教学目的，即学生理解了知识. “生根”比喻事物建立起牢固的基础，教学中素养生根指在理解知识的基础上牢固知识、迁移知识、运用知识. “发展”指事物由小到大、由简单到复杂、由低级到高级的变化，教学中素养发展指类比拓广知识，即让学生学会创新. 《课标》在“数学学科核心素养的水平划分”中，详细地阐述了六大素养水平的三个层次，可概括为“水平一：在熟悉情境中，能解决具体问题，了解和体会数学知识”“水平二：在关联情境中，能解决一类问题，理解和构建数学知识”“水平三：在综合情境中，能形成新命题，即创造性解决问题，掌握和运用数学知识”. 综上所述，若能够正确解答问题，可以认为达到了数学核心素养水平一的层次，使数学核心素养在知识理解中落地；若能够将已知数学问题推广至更一般的情形，并给出相应且合理的解释和证明，可以认为达到了数学核心素养水平二的层次，使数学核心素养在知识迁移中生根；若能够理解知识本质，进而类比拓广，形成一般性结论，可以认为达到了数学核心素养水平三的层次，使数学核心素养在知识创新中发展.

1. 数学核心素养落地：一题多解，知识理解

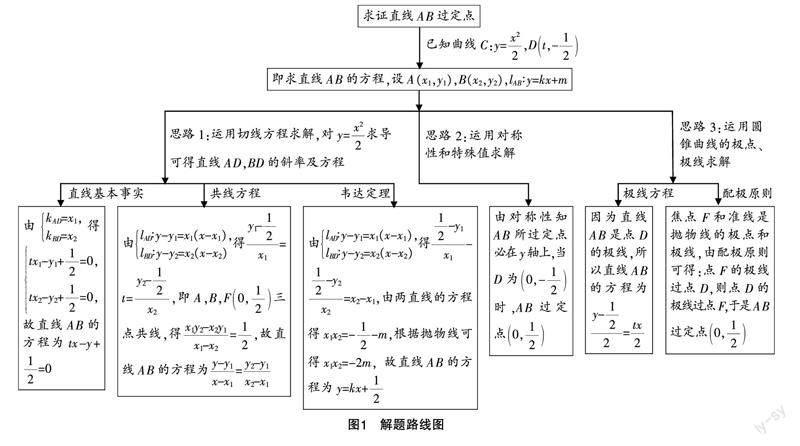
针对本题，学生通常用切线方程求直线AB的方程，然后得出定点，其他解法考虑较少，这体现着学生思维的惰性和局限性. 因此，在解题教学中，教师不能只关注常规解法和解题技巧，还要多关注问题的本质和发散的思维，可通过一题多解促使学生全面理解问题的本质. 图1列举了三种思路、六种解法，涉及直线基本事实、共线方程、韦达定理、配级原则等知识，包含对称、降次、转化等数学思想. 无论运用哪种方法解题，学生都需要理解基本的抛物线知识，因此，若学生能给出正确的解题过程，可以认为学生达到了数学核心素养水平一的层次.

知识落脚在于理解，《义务教育数学课程标准（2011年版）》指出：描述对象的由来、内涵和特征，阐述此对象与相关对象之间的区别和联系［8］. 讲解该题时，先让学生阅读题目，理解问题指向，提取可用信息，再细化处理问题，推断出隐含信息. 除了让学生理解常规解法，教师还要追问是否存在其他不同的解法或思路，并给予提醒以及充足的时间让学生去思考. 可让学生上台展示不同的解法，教师给补充，并系统汇总与归纳多种解法，让学生认识到不同解法间的关联与差异，从而真正理解知识的本质. 在教学中，教师要促使学生思考，如提出一些延伸性问题，或者跳出当下的知识点，追问学生放到学过的关联知识中是否可行，让学生在耳濡目染下形成发散和深度思考的好习惯，从而转变学生“就题论题”“唯分是从”的价值观念. 汇总时可以绘制图1所示的解题路线图，也可以使用图表、表格等其他形式进行梳理，这罗列的不仅是解法，更是思维. 通过对问题的多角度思考，学生会尝到“横看成岭侧成峰，远近高低各不同”的味道，在不同解法或思路中“深刻理解”知识，使数学核心素养在知识理解中落地.

2. 数学核心素养生根：问题推广，知识迁移

观察法是人类发展史上最原始的方法，解决完问题不是结束而是开始，应多让学生去观察和反思，引导学生发现问题、提出新的问题.一个班有几十个学生，总有不同的想法和做法，俗话说“三个臭皮匠抵一个诸葛亮”，他们千奇百怪的想法也许会给教师带来意外惊喜. 当然，教师设问应极具技巧性，需具体无歧义、指向明确.例如本题，能发现点D恰好在抛物线的准线上，所求定点恰好与抛物线的焦点相同，于是可提问：其他抛物线准线上的点是否也有这样的性质呢？定点还会是抛物线的焦点吗？引导学生猜想后证明结论：对于抛物线C，D为抛物线C的准线上的动点，过D作C的两条切线，切点分别为A，B，则直线AB恒过抛物线C的焦点.

知识生长即理解知识间的关联性、把握数学问题的本质、明晰数学的通性通法，即将知识迁移到一般化的关联情境中. 对于有价值的数学问题，就应充分挖掘其价值，解题不流于表层，适时将具体问题抽象推广至一般化，让学生经历感性猜想到理性证明的过程，从理解一道题上升为一类题，有效促进学生数学抽象、数学运算和逻辑推理等素养的提升. 学生若能在理解问题本质的前提下升华，即对知识进行迁移，可认为学生达到了数学素养水平二的层次，使得数学核心素养在知识迁移过程中生根.

3. 数学核心素养的发展：拓展延伸，知识创新

知识创新是在原有知识框架的基础上，将知识进一步延伸，得出新的结论或命题. 延伸的最好办法就是搭建知识框架，建立纵横联系——单元教学就是一个典型的例子. 回归本题，考查的虽是抛物线，但圆、抛物线、椭圆、双曲线均是圆锥曲线，其存在某些共同特征，因此教师可引导学生将上述问题类比延伸到圆、椭圆、双曲线中，使学生形成研究问题的思路和方法，揭示其内在联系，激活自身思维. 多数学生进行类比只是单纯的模仿，形似而神不似，问其缘由却说不出所以然，因此教学中教师要归纳本质、建立联系，帮助学生实现“知其然”到“知其所以然”再到“何由以知其所以然”的跨越.

（1）类比椭圆.

对于椭圆C，D为椭圆C的准线上的动点，过D作C的两条切线，切点分别为A，B，求证：直线AB恒过椭圆与准线同侧的焦点.

在原题结论的基础上进行类比、改写，合情推理出椭圆对应的结论，进一步考验学生的数学抽象能力和逻辑推理能力，关键在于打开思维，将合情推理的结论演绎证明出来，彰显数学的严谨性. 在教学中，教师要通过设问激发学生思考，引导学生通盘考虑、全盘整合椭圆和抛物线的相关知识，运算和处理相关数据，形成有逻辑条理的证明过程.

（2）类比双曲线.

对于双曲线C，D为双曲线C的准线上的动点，过D作C的两条切线，切点分别为A，B，求证：直线AB恒过双曲线与准线同侧的焦点.

探究雙曲线的情况时，教师可以让学生仿造椭圆情况下的研究思路和方法，给学生搭建合作交流的平台，有的放矢地把控全局，将思维训练和素养培育贯穿始终，进一步整合圆锥曲线知识.

（3）结论推广.

通过总结，引导学生跳出单一的局面，从整体上去思考圆锥曲线，教师可以通过问题驱动引导学生提炼总结，揭示其中的内在联系，更好地建构知识体系，完善认知结构，使知识从零散的记忆逐步走向完整、系统的理解.

结论1：一般地，对于任意抛物线，D为抛物线的准线上的一个动点，过点D作抛物线的两条切线，切点分别为A，B，则直线AB恒过抛物线的焦点.

结论2：一般地，对于任意椭圆（双曲线），D为椭圆（双曲线）的准线上的一个动点，过点D作椭圆（双曲线）的两条切线，切点分别为A，B，则直线AB恒过椭圆（双曲线）与准线同侧的焦点.

综上所述，从抛物线的相关结论延伸到椭圆与双曲线（圆是特殊的椭圆，不再赘述），再到圆锥曲线整体认知建构，从局部到整体，从具体到一般，在综合情境中高度概括出圆锥曲线的一般结论，形成数学命题，达到数学核心素养水平三的层次.

结语

在圆锥曲线问题教学中，教师要挖掘问题背后的知识本质以及所蕴含的思想方法，只有深入研究才能更清楚地认识到问题的价值，才能在教学中充分发挥问题的教育价值. 此外，要注重圆锥曲线整体认知建构，引导学生亲历理解、迁移、归纳类比和演绎证明的过程，揭示圆、抛物线、椭圆、双曲线之间的内在联系，感悟数学思想方法，将学习的外部知识内化为内部能力，形成个人素养. 本文利用一个典型的开放式圆锥曲线问题，通过多角度思考、多层次探索、多方面推广，先由一题多解的方式促使学生理解知识，促使数学核心素养落地；再由问题的进一步拓展促使学生迁移知识，达成数学核心素养生根；最后由类比推广形成一般性结论，达成数学核心素养发展.从整个过程体会数学核心素养在数学问题教学中如何落地、生根、发展.

参考文献：

［1］ 中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［2］ 邵贵明，胡典顺，柳福祥. 论数学核心素养在高中数学课堂落地生根——以人教版高中“对数”教学为例［J］. 数学教育学报，2020，29（06）：46-50.

［3］ 王海青. 问题驱动理论下“圆锥曲线与方程”教学重构［D］. 广州大学，2019.

［4］ 王亚运. HPME视角下的椭圆教学设计与研究［D］. 华中师范大学，2017.

［5］ 张俊忠.数学开放题的起源、价值与运用［J］. 教学与管理，2020（31）：43-45.

［6］ 杨亮. 审读高考题的三重境界［J］. 思想政治课教学，2017（04）：54-55.

［7］ 中国社会科学院语言研究所词典编辑室. 现代汉语词典［M］. 北京：商务印书馆，2012.

［8］ 中华人民共和国教育部. 义务教育数学课程标准（2011年版）［M］. 北京：北京师范大学出版社，2011.

作者简介：石义娜（1996—），硕士研究生，从事数学教育研究工作.