DCM模拟中基于OPSA方法的参数敏感性分析

高永丽, 王际朝, 孙国栋, 张 坤, 姜向阳, 王 宁

DCM模拟中基于OPSA方法的参数敏感性分析

高永丽1, 王际朝1, 孙国栋2, 张 坤3, 姜向阳4, 王 宁4

(1. 中国石油大学(华东), 山东 青岛 266580; 2. 中国科学院大气物理研究所, 北京 100029; 3. 中国科学院海洋研究所, 山东 青岛 266071; 4. 山东省海洋资源与环境研究院, 山东 烟台 264006)

深层叶绿素最大值(deep chlorophyll maximum, DCM)现象是海洋与湖泊中普遍存在的生态现象。对其进行数值模拟时, 参数不确定性是导致模拟结果出现误差的重要原因。基于一个经典海洋生态模式(nutrients-phytoplankton model, NP), 本文通过最优参数敏感性分析(optimization parameter sensitivity analysis, OPSA)方法探讨了模式参数不确定性对DCM模拟的影响。研究表明, 背景场浑浊度、垂向湍流扩散系数、浮游植物营养盐含量和硝酸盐再循环系数为模式中的敏感参数, 它们的扰动将导致DCM模拟发生显著改变。进一步, 设计观测系统模拟试验评估了消除敏感参数误差DCM模拟的改进程度。结果显示, 去除4个敏感参数误差DCM模拟平均改进了56.83%, 约是去除不敏感参数误差平均改进程度(4.51%)的13倍。而且, 去除敏感参数误差模拟改进的稳定性更好, 变异系数仅为9.44%, 去除不敏感参数误差模拟改进的变异系数达到了14.76%, 稳定性较差。据此, 可优先发展与敏感参数直接相关的动力过程参数化方案, 或在有限的观测资源下优先对敏感参数展开目标观测, 进而为提高DCM模拟与预测提供科学指导。

DCM; 参数敏感性; 最优扰动; OPSA方法; 目标观测

在海洋、湖泊等大部分水体中, 叶绿素垂向分布的最大值并不出现在水体表面, 而是出现在水面下一定深度的地方[1], 这就是DCM(deep chlorophyll maximum)现象。早在1965年, Yentsch[2]就发现在印度洋相对稳定的水体结构中, 物理与生物的耦合作用使得浮游植物在真光层底部出现最大值。随后, 更多研究证实了该现象在其他大洋、湖泊, 甚至混合作用较弱的河口区也普遍存在[3]。DCM现象体现了浮游植物对光和营养盐的适应性, 研究DCM现象对探究海洋生态系统的结构与功能具有十分重要的意义, 因此一直是国内外海洋生态动力学领域关注的热点之一[4-5]。

随着高性能计算的快速发展, 数值模式逐渐成为海洋环流及海洋生态动力学研究的重要工具[6-7]。与观测相比, 数值模拟结果通常存在偏差。其中, 模式参数误差是导致模拟结果不确定性的主要原因之一。海洋生态模式中含有大量与描述物理、生物化学过程相关的参数。这些参数的预设值只有很少一部分是由实际观测获得, 其余大部分是通过经验、半经验或者统计方法得到的估计值, 因此具有较大的不确定性[8]。通过参数敏感性分析探究模式中参数不确定性影响到底如何, 识别相对敏感的参数, 并且集中有限的人力物力资源优先对敏感参数展开观测, 对提高数值模拟技巧是非常重要的。

然而, 围绕模式参数的敏感性分析是一个复杂的问题。早期研究中, 人们普遍使用的是数据同化方法, 例如非线性优化技术[9], 伴随方法[10]和弱约束参数估计方法[11]等。此类方法通过调整参数值使得模式输出与观测数据的偏差达到最小, 并以此确定最优参数值。在此基础上, 根据参数误差与模式输出变化之间的关系, 分析参数的敏感性。这些方法需要提供状态变量和相关参数的初猜值, 且未能考虑参数间的相互作用, 因此具有一定的局限性。Chu等[12]发展了一种基于方差的非线性方法, 通过定义的敏感性指标刻画了浮游植物生物量对12个模式参数的相对敏感性, 并利用二阶敏感性指标分析了参数两两组合的非线性相互作用对模拟结果的影响。近年来, Mu等[13]基于对海洋模式中初始误差的研究, 又提出了条件非线性最优参数扰动方法。该方法考虑了参数扰动间的非线性相互作用, 可识别那些在目标时刻对所关注的自然事件的模拟或预报产生最大影响的重要参数或参数组合[14-15]。

事实上, 在一些数值模式(特别是生态模式)中, 模式参数可能多达10~50个。在此情形下, 使用以上方法识别敏感参数, 并考察参数扰动间的非线性相互作用时, 将耗费相当大的计算量。为此, Wang等[16]提出了优化参数敏感性分析方法(OPSA), 该方法旨在辨别出“累计”影响都非常小的参数扰动(不敏感参数), 进而识别出相对敏感的参数。该方法在识别敏感参数时能大大节约计算资源, 目前已成功应用于黑潮延伸体模态转变过程等研究[17]。

本文基于OPSA方法和经典海洋生态模式(nut­rients-phytoplankton model), 识别出四个相对敏感的参数, 并利用敏感性试验验证了去除敏感参数误差确实能有效提高模拟技巧, 最后讨论了基于敏感参数优先实施目标观测的可靠性。

1 方法与模式介绍

1.1 OPSA方法

假设以()为状态变量的数值模式如下:

()=M()(0) (1)

则去除扰动中参数p的扰动p(1≤≤)后,()的改变量如下:

假设扰动=(1,2, …,p)的约束范围为ε, 构建如下最优化问题:

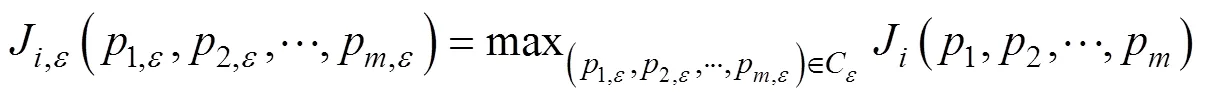
利用最优化算法, 如遗传算法(differential evolution)、谱梯度算法(spectral gradient algorithm)等求解上述最优化问题, 即得导致模式误差出现最大值J的一类参数扰动(p,p,…, p)。

接下来, 考察多个参数同时发生扰动引起的模式误差。令:

则参数扰动p与p(1≤≤)导致的“联合误差”为:

类似地, 可定义三个或更多参数同时发生扰动导致的模式误差。又因为:

, (8)

故:

由公式(9)可知, 考虑参数扰动间的非线性相互作用时, 任意两个参数扰动导致的最大模式误差一定不超过两个单参数扰动引起的最大误差之和。因此, 在用OPSA方法进行敏感性分析时, 只需求解针对单参数扰动构建的非线性优化系统, 多参数扰动导致的模式误差可用相应单参数扰动导致的误差累积来度量, 这就省去了优化多参数扰动的计算量, 大大节约了计算资源。

1.2 NP模式

NP模式是描述海洋生态系统动力过程的一维垂向数值模式, 不考虑物质的水平运输, 常用来研究海洋和湖泊中浮游植物的垂向分布趋势[18-19], 特别是DCM现象的模拟。Huisman等[20]在研究DCM振荡与混沌现象时指出, 虽然NP模式只是一个理论模式, 但它呈现了许多与真实海洋环境中DCM现象一致的特征。例如, 模式模拟的DCM深度在100 m左右, 且DCM所在位置以上的营养盐浓度接近于0、以下的营养盐浓度是线性增加的, 这些表现与Klausmeier和Litchman对观测资料的分析得出的结论是一致的[21]。因此, 虽然海洋生态系统的数值模式越来越呈现出复杂化的趋势, NP模式仍然经常被用来研究叶绿素的垂向分布及其对物理过程的响应机制[22]。

在NP模式描述的非线性系统中, 浮游植物生长受到光的强度与营养盐浓度的限制, 浮游植物()和营养盐()的动力学过程满足如下的一维反应扩散方程:

其中,代表水柱的深度,代表时间,代表垂向湍流扩散系数。和分别代表浮游植物死亡率和下沉速率,和分别代表浮游植物细胞的营养盐含量和死掉的浮游植物参与营养盐再循环的系数,H和H分别代表营养盐和光的半饱和常数。诸参数值见表1。

表1 NP模式中的参数设置

另外, 来自太阳辐射的入射光在水面下的传播满足Lambert-Beer’s方程[4]:

其中,in代表入射光在水面的光强。

假设浮游植物和营养盐在模式的上下边界都没有通量交换, 且营养盐在水柱的底部保持不变:

此处,N表示营养盐在水柱底部Z处的值, 本文中=10 mmol/m3。

2 参数敏感性分析

2.1 试验设置

为了构建求解最优参数扰动的非线性优化系统, 首先进行以下试验设置。

2.1.1 选取参考态

设定水柱的深度是300 m, 空间步长是0.05 m, 时间步长是0.1 h, 模式中所有参数值见表1。采用向前差分格式将NP模式的控制方程组[公式(10)]离散化, 并且积分20 a。

在积分时间超过8 a时, 模式达到平衡态。此时, 随着表层营养盐的消耗, 在水面下一定深度处,

图1 一维NP模式中营养盐和浮游植物的时空演变及系统达到平衡态后的垂直分布

来自水柱底部的营养盐与来自水面的入射光达到平衡(图1 a)。浮游植物在此大量繁殖, NP模式呈现出稳定的DCM特征(图1 b)。图1 c表明, 在平衡态下, 营养盐从下往上逐渐扩散, 从DCM所在位置到水柱底部是线性增加的, 表层营养盐几乎接近于0。同时, 浮游植物生物量的最大值出现在水面下84 m, 浮游植物的生存区间主要集中在水面下50~ 150 m内(图1 d), 这与许多研究中呈现的DCM模拟结果是一致的[14, 23]。可见, DCM现象是浮游植物对光和营养盐适应性竞争的结果, 研究DCM现象对理解海洋生态系统动力过程有着极为重要的意义。为考察参数扰动引起的模拟误差大小, 在下面的敏感性分析中, 将积分终止时刻的平衡态作为扰动的参考态。

2.1.2 扰动约束及目标函数

另外, 为了度量该扰动引起的DCM变化, 将水柱上各点浮游植物变化量的2范数定义为目标函数[参考公式(4)], 具体表达式如下:

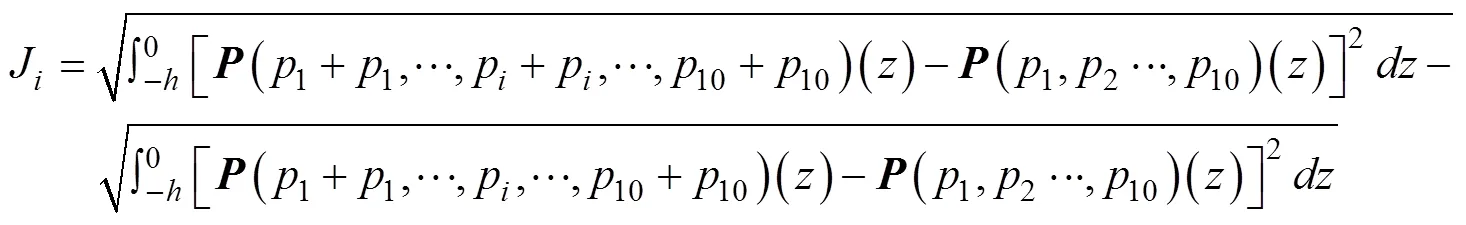
其中,为水柱的深度。

2.1.3 阈值

在用OPSA方法进行参数敏感性分析时, 求解每个参数对应的优化问题[公式(5)]后, 可对所得的最大模拟误差进行排序:1,ε≤2,ε≤…≤10,ε, 其中J,ε(1≤≤)为相应参数扰动在约束=0.1下所引起的最大目标函数值。接下来, 为了确定哪些参数较为敏感, 需要确定阈值。假设1,+2,+…J,≤,1,+2,+…J,+J,>(+1≤10), 则认为1,、2,…J,对应的参数扰动引起的模拟误差的最大值仍然较小, 相应的参数被视为不敏感参数, 而J+1,、J+2,…10,对应的参数则为相对敏感参数。

由此可见, 阈值的选取对于用OPSA方法识别敏感参数是非常关键的。在实际应用中, 往往是根据所研究的具体问题来设置的。考虑到不同水体中的海洋生态系统, 浮游植物浓度有着较大差异[24]。且即使是同一水体中, 不同年份的同一季节, 因气候和水文环境差异导致的浮游植物生物量也有很大不同[25]。当水体富营养化时, 还会出现浮游植物过量繁殖的水华现象, 这时浮游植物生物量可能达到平时的几倍[26]。因此, 为了考察参数不确定性对DCM模拟的影响程度, 本文中假设水柱各点浮游植物生物量的变化最大不超过参考态的一倍, 则计算可得相应的目标函数值为8.441 2×108, 以此作为来判断累计参数扰动引起的模拟误差是否达到阈值。

2.2 最优化试验

本节中的最优化试验是如下设计的: 首先分别计算对所有参数全部叠加扰动以及在此基础上逐一去掉其中某个参数扰动所对应的模拟误差, 然后将二者的差作为目标函数, 对所有参数扰动进行优化(优化维数为10维), 即得到相应的最优扰动及最大模拟误差。这里, 为了逐个求解每个参数扰动导致的最大模拟误差, 共进行了10次优化试验。

其中, 寻找使目标函数达到极大值的最优参数扰动, 需要求解非线性最优化问题[公式(5)]。为此, 选择谱投影梯度算法[27](spectral projected gradient, SPG)。该方法除需要提供约束条件和目标函数外, 还需要目标函数关于参数扰动的梯度信息(根据梯度定义计算), 具体计算过程可参考文献[28]。另外, 为使模式重新达到平衡态, 优化时间为3年。且考虑到NP模式在迭代500次左右已逐渐达到平衡态, 因此迭代次数设置为1 000次。

为考察单参数的敏感性, 求解最优化试验所得的最优参数扰动见表2。其中, 参数3(浮游植物死亡率)的不确定性影响最大时, 各参数扰动全部位于约束边界。其余参数对应的最优扰动中, 各参数扰动并没有全部达到边界值。由此可见, 多参数同时发生扰动引起的动力过程变化之间确实存在非线性相互作用。在进行参数敏感性分析时, 必须考虑这种非线性相互作用带来的影响, 才能对非线性系统进行合理的量化分析。

表2 考察单参数敏感性所得的最优参数扰动

表3是求解上述优化试验得到的目标函数值。可见, 参数1(硝酸盐半饱和常数)的不确定性影响最小, 参数9(背景场浑浊度)的不确定性影响最大。各目标函数值的变化范围从0.192到5.335, 最小值与最大值相差近30倍。因此, 在数值模拟中参数扰动的不确定性影响相差很大, 对它们进行敏感性分析, 从而确定最优参数化方案和观测方案是非常有必要的。接下来, 将表3中的目标函数值按从小到大的顺序进行排序(图2 a), 依次为:1、4、10、2、3、8、5、6、7和9, 然后逐个进行叠加并与阈值比较。

表3 考察单参数敏感性所得的目标函数值

图2 各参数的目标函数值及累加的(按从小到大的顺序)目标函数值排序

注: 其中代表设定的阈值; (b)中横轴刻度“…P”表示从前一参数对应的目标函数值累加到P对应的目标函数值

图2 b表明, 参数1、4、10、2、3和8所对应的目标函数值累加后仍未达到给定的阈值, 即所允许的最大模式误差。由公式(5)可知, 这6个参数同时发生扰动导致的模式误差不超过它们各自扰动导致的模式误差之和, 因此将这6个参数被视作相对不敏感参数。其他参数5(垂直湍流扩散系数)、6(浮游植物营养盐含量)、7(硝酸盐再循环系数)和9(背景场浑浊度)则为敏感参数。

事实上, 在海洋生态系统中, 垂直湍流扩散(5)除了对浮游植物的接触率、摄食率和生长率有直接影响外, 还在很大程度上影响着营养盐的输送[7], 是对生态系统起着关键作用的物理过程。浮游植物营养盐含量(6)与硝酸盐再循环系数(7)则体现了系统中浮游植物死亡后营养盐的再次利用。而背景场浑浊度(9)影响的是光的入射率, 反映了光对该生态系统的控制作用。可见, 敏感参数既包含物理参数, 又有描述生态动力过程的参数, 直接或间接影响着营养盐和光这两大海洋生态系统的主要因素, 在很大程度上影响着模拟结果的准确性。

2.3 观测系统模拟试验(observing system simulation experiment, OSSE)

在上一小节中, 通过优化得到相应的最优扰动及其所导致的最大模拟误差, 并由此识别出敏感参数为5、6、7和9。那么去除敏感参数误差, DCM模拟是否一定会得到改进, 具体改进程度如何呢？为此, 本小节将通过观测系统模拟试验(OSSE)来回答这一问题。

如图3所示, OSSE试验包含真值试验, 控制试验和同化试验。具体地, 真值试验即参数均未发生扰动时的DCM模拟(参考态); 对真值试验中的10个参数叠加100组随机误差并计算由此导致的模拟偏差即为控制试验; 最后计算去除其中部分参数误差(敏感/不敏感)后的模拟偏差作为同化试验。在此基础上, 用下式度量DCM模拟的改进程度:

图3 OSSE试验设计图

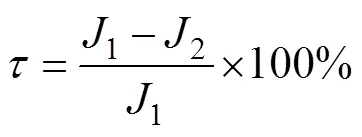
其中,1为控制试验导致的模拟误差,2为同化试验导致的模拟误差。此处, 共进行了两组同化试验, 包括去除敏感参数误差和去除不敏感参数误差(图4)。这里,值为正表示去掉部分参数误差后, DCM模拟得到了改进, 而值为负, 则可能是由参数扰动间的非线性相互作用导致的。若去除的部分参数误差跟剩余的参数误差之间是相互“抑制”的关系, 去除这部分参数误差后, 导致的模拟结果就可能更差。

图4 观测系统模拟试验结果

Fig. 4 Results of OSSE experiments: removing the perturbations sensitive/insensitive parameters

据图4 a, 当去除敏感参数误差时, 100组随机试验中有95组的DCM模拟都得到了改善, 且改善均值为56.83%; 当去除不敏感参数误差时, 100组随机试验中只有64组的DCM模拟得到了改善, 改善均值仅为4.51%(图4 b)。由此可见, 识别敏感参数后, 有针对性地去除敏感参数误差, 确实能有效提高DCM模拟水平。

仅考虑模拟改进程度的大小, 不能保证去除敏感参数随机误差后DCM模拟一定会得到改善, 还需考察去除敏感参数误差后模拟改进效果的稳定性。为此, 使用变异系数(coefficient of variation)进一步考察OSSE试验所得两组数据的相对离散程度, 公式如下:

其中,和分别为数据的标准差和均值。

由图5, 去除敏感参数误差所得DCM模拟的改进程度, 其变异系数为9.44%; 而去除不敏感参数误差所得DCM模拟的改进程度, 其变异系数为14.76%。由此可见, 去除模式中敏感参数的误差, 大多数情况下DCM模拟都得到了改进, 且波动较小, 变异系数也在合理的范围之内。去除不敏感参数误差, DCM模拟的改进则很有限, 变异系数已接近15%。因此, 先识别敏感参数, 再优先改进敏感参数误差, 对于提高DCM模拟技巧是可靠的。

图5 改进敏感/不敏感参数误差所得深层叶绿素最大值模拟的变异系数

进一步, 将去除敏感/不敏感参数扰动的所得的浮游植物生物量垂向分布取均值, 考察DCM位置与强度的变化。由图6a可见, 与叠加所有参数扰动相比, 去除敏感参数扰动后DCM位置与强度都发生了很大改变, 且已与参考态非常接近。而去除不敏感参数扰动后DCM并没有较大变化(图6b中红线与蓝线几乎重合), 仍然远离参考态。可见, 识别具有较大不确定性的敏感参数对于改进DCM模拟是非常重要的, 去除敏感参数误差DCM模拟的改进非常明显。这在含有大量参数尚未经由观测明确的海洋生态数值模式中, 显得尤为重要。

图6 分别改善敏感参数误差/不敏感参数误差后, 浮游植物的垂向分布

3 结论与讨论

本文基于OPSA方法探讨了DCM数值模拟中的参数敏感性:

1) 求解所建立的非线性优化系统, 发现最优扰动中单个参数的扰动并不总是位于边界上, 不同参数扰动间确实存在非线性相互作用。

2) 针对DCM模拟, 根据OPSA方法识别的不敏感参数为:1、4、10、2、3和8, 敏感参数为:5(垂直湍流扩散系数)、6(浮游植物营养盐含量)、7(硝酸盐再循环系数)和9(背景场浑浊度)。

3) OSSE试验表明, 对模式参数叠加100组随机扰动, 去除敏感参数扰动后有95组的DCM模拟都得到了改进, 平均改进程度为56.83%; 而去除不敏感参数扰动, 仅有64组的DCM模拟得到了改进, 平均改进程度仅为4.51%。因此识别敏感参数对改进DCM模拟有着重要意义。

次表层的浮游植物贡献了水体中绝大部分初级生产力, 因此人们对浮游植物的垂向分布非常关注。在用数值模式对DCM现象进行数值模拟时, 参数扰动对模拟结果具有很大影响。基于OPSA方法识别的敏感参数为5、6、7和9, 这与使用条件非线性最优参数扰动方法(CNOP-P)识别的敏感参数组合是一致的[14]。三个直接影响营养盐分布的参数(垂向湍流扩散、浮游植物营养盐含量、硝酸盐再循环系数)与光的限制参数(背景场浑浊度)是影响浮游植物垂向分布的最主要因素。本研究使用OPSA方法共求解了10次非线性优化系统(10维), 而使用条件非线性最优扰动方法则进行了210次最优化试验(4维)才识别出四个敏感参数, 前者大大节约了计算量。事实上, 随着数值模式复杂程度越来越高, 模式中参数个数也越来越多, 使用OPSA方法能以较小的计算量识别敏感参数的优势将更加凸显。

此外, OSSE试验证实去除敏感参数扰动能更好地改进数值模拟技巧。因此, 一方面可借助参数敏感性分析优先发展与敏感参数直接相关的动力过程参数化方案, 有效节省计算时间与机时消耗。另一方面, 考虑到开展大范围的海洋观测往往消耗巨大, 也可基于参数敏感性分析识别的敏感参数, 利用有限的观测资源优先对敏感参数展开观测。这正是目标观测的思想[29]。进而据此对模式进行校正, 可使其提供更好的模拟与预报。

作为中国三大河口三角洲之一的黄河三角洲, 在环渤海地区发展中具有重要的战略地位。该区域生态系统独具特色, 处于大气、河流、海洋与陆地的交接带, 是世界上典型的河口湿地生态系统。基于OPSA方法, 识别敏感参数, 优先发展与敏感参数直接相关的动力过程参数化方案, 可有效提高黄河三角洲生态系统的模拟与预报技巧。在此基础上开展目标观测研究, 科学指导黄河三角洲区域生态环境监测网络的建设, 对于推动区域海洋经济高质量发展具有重要意义。

[1] 倪晓波, 黄大吉. 海洋次表层叶绿素最大值的分布和形成机制研究[J]. 海洋科学, 2006, 30(5): 58-64.

NI Xiaobo, HUANG Daji. Subsurface chlorophyll maximum: its temporal-spatial distribution and formation mechanism in the ocean[J]. Marine Sciences, 2006, 30(5): 58-64.

[2] YENTSCH C S. Distribution of chlorophyll and phaeo­phytin in the open ocean[J]. Deep-Sea Research and Oceanographic Abstracts, 1965, 12(5): 653-666.

[3] ABBOTT M K. Mixing and the dynamics of the deep chlorophyll maximum in the Lake Tahoe[J]. Limnology and Oceanography, 1984, 29(4): 862-878.

[4] EVANS G T, PARSLOW J S. A model of annual plankton cycles[J]. Biological Oceanographic, 1985, 3(3): 327-347.

[5] LONGHURST A R. Toward an ecological geography of the sea[M]. Amsterdam, Netherlands: Elsevier, 1998.

[6] OMLIN M, BRUN R, REICHERT P, et al. Biogeochemical model of Lake Zürich: sensitivity, identifiability and uncertainty analysis[J]. Ecological Modelling, 2001, 141(1/3): 105-123.

[7] JPLLIFF J K, KINDLE J C, SHULMAN I G, et al. Summary diagrams for coupled Hydrodynamic-Eco­system model skill assessment[J]. Journal of Marine Systems, 2009, 76(1/2): 64-82.

[8] KEVIN C R, LUKE A W, JORDAN S R, et al. Improving the precision of lake ecosystem metabolism estimates by identifying predictors of model uncertainty[J]. Limnology and Oceanography Methods, 2014, 12(5): 303-312.

[9] FASHAM M J R, EVANS G T. The use of optimization techniques to model marine ecosystem dynamics at the JGOFS station at 47°N 20°W[J]. Philosophical Transactions of the Royal Society of London B Biological Sciences, 1995, 348(1324): 203-209.

[10] EVENSEN G, DEE D P, SCHRÖTER J, et al. Parameter estimation in dynamical models[J]. CHASSIGNET E P, VERRON J. Ocean modeling and parameterizations, NATO Science Series, 1998, 516: 373-398.

[11] LOSA S N, KIVMAN G A, RYABCHENKO V A, et al. Weak constraint parameter estimation for a simple ocean ecosystem model: what can we learn about the model and data?[J]. Journal of Marine Systems, 2004, 45(1/2): 1-20.

[12] CHU P C, IVANOV L M, MARGOLINA T M, et al. On non-linear sensitivity of marine biological models to parameter variations[J]. Ecological Modelling, 2007, 206(3/4): 369-382.

[13] MU M, DUAN W S, WANG Q, et al. An extension of conditional nonlinear optimal perturbation approach and its applications[J]. Nonlinear Processes Geophysics: 2010, 17(2): 211-220.

[14] GAO Y L, MU M, ZHANG K, et al. Impacts of parameter uncertainties on deep chlorophyll maximum simulation revealed by the CNOP-P approach[J]. Journal of Oceanology and Limnology, 2020, 38(5): 1382- 1393.

[15] SUN G D, MU M. The analyses of the net primary production due to regional and seasonal temperature differences in eastern China using the LPJ model[J]. Ecological Modelling: 2014, 289: 66-76.

[16] WANG Q, TANG Y. An optimization strategy for identifying parameter sensitivity in atmospheric and oceanic models[J]. Monthly Weather Review, 2017, 145(8): 3293-3305.

[17] WANG Q, PIERINI S, TANG Y, et al. Parameter sensitivity analysis of the short-range prediction of Kuroshio extension transition processes using an optimization approach[J]. Theoretical and Applied Climatology, 2019, 138(3/4): 1481-1492.

[18] 高永丽. 垂向湍流扩散系数的不确定性对深层叶绿素最大值现象模拟的影响[J]. 海洋科学, 2019, 43(2): 34-40.

GAO Yongli. A study of uncertainty related to the coefficient of vertical turbulence diffusion in ocean ecosystem model[J]. Marine Sciences, 2019, 43(2): 34-40.

[19] HODGES B A, RUDNICK D L. Simple models of steady deep maxima in chlorophyll and biomass[J]. Deep Sea Research Part I: Oceanographic Research Papers, 2004, 51(8): 999-1015.

[20] HUISMAN J, PHAM T N, KARL D M, et al. Reduced mixing generates oscillations and chaos in the oceanic deep chlorophyll maximum[J]. Nature, 2006, 439(7074): 322-325.

[21] KLAUSMEIER C A, LITCHMAN E. Algal games: The vertical distribution of phytoplankton in poorly mixed water columns[J]. Journal of Oceanology and Limnology, 2001, 46(8): 1998-2007.

[22] LICCARDO A, FIERRO A, IUDICONE D, et al. Response of the deep chlorophyll maximum to fluctuations in vertical mixing intensity[J]. Progress in Oceanography, 2013, 109: 33-46.

[23] WANG Q, MU M. A new application of conditional nonlinear optimal perturbation approach to boundary condition uncertainty[J]. Journal of Geophysical Research: Oceans, 2015, 120(12): 7979-7996.

[24] BOYCE D G, MARLON R L, BORIS W, et al. Global phytoplankton decline over the past century[J]. Nature, 2010, 466(29): 591-466.

[25] MCQUATTERS-GOLLOP A, REID P C, EDWARDS M, et al. Is there a decline in marine phytoplankton?[J]. Nature, 2011, 472(7342): E6-E7.

[26] BOYD P W, WATSON A J, LAW C S, et al. A mesoscale phytoplankton bloom in the polar Southern Ocean stimulated by iron fertilization[J]. Nature, 2000, 407(6805): 695-702.

[27] BIRGIN E G, MARTÍNEZ J M, RAYDAN M, et al. Nonmonotone spectral projected gradient methods on convex sets[J]. SIAM Journal of Optimization, 2000, 10(4): 1196-1211.

[28] LIU X, MU M, WANG Q, et al. The nonlinear optimal triggering perturbation of the Kuroshio large meander and its evolution in a regional ocean model[J]. Journal of Physical Oceanography, 2018, 48(8): 1771-1786.

[29] 张坤, 穆穆, 王强. 数值模式在海洋观测设计中的重要作用: 回顾与展望[J]. 中国科学: 地球科学, 2021, 51(5): 653-665.

ZHANG Kun, MU Mu, WANG Qiang. Increasingly important role of numerical modeling in oceanic observation design strategy: A review[J]. Science China Earth Sciences, 2021, 51(5): 653-665.

Parameter sensitivity analysis of a biological ocean model based on OPSA method

GAO Yong-Li1, WANG Ji-chao1, SUN Guo-dong2, ZHANG Kun3, JIANG Xiang-yang4, WANG Ning4

(1. China University of Petroleum (East China), Qingdao 266580, China; 2. Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China; 3. Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China; 4. Shandong Marine Resources and Environment Research Institute, Yantai 264006, China)

The deep chlorophyll maximum (DCM) is a common ecological phenomenon in oceans and lakes. Numerical simulation has emerged as an important tool for studying this phenomenon, and parameter uncertainty is a primary source of uncertainty in the simulations. By optimization parameter sensitivity analysis, the sensitivities of 10 parameters in the nutrient–phytoplankton model related to DCM simulation were investigated. The results revealed the sensitive parameters in the DCM simulation to be background turbidity, vertical turbulent diffusion, nutrient content of phytoplankton, and recycling coefficient of nitrate; perturbations in these parameters lead to considerable changes in the DCM. In addition, the observing system simulation experiment was designed to evaluate the improvement in DCM simulation while eliminating sensitive parameter errors. The results revealed that the average improvement in DCM simulation resulting from the removal of the sensitive parameter errors is 56.83%, which is approximately 13 times that obtained from the removal of the insensitive parameter errors (4.51%). Moreover, the coefficient of variation was calculated to examine the stability of simulation improvement. The values obtained were 9.44% for the removal of sensitive parameter perturbations and 14.76% for the removal of insensitive parameter perturbations, indicating decreased stability. This study suggests that prioritizing the parameterization scheme and target observation related to sensitive parameters may provide valuable insights for the advancement of DCM simulations and predictions.

DCM; parameter sensitivity; optimal perturbation; OPSA; target observation

May 17, 2022

731.26

A

1000-3096(2023)5-0139-10

10.11759/hykx20220517003

2022-05-17;

2022-07-18

国家自然科学基金项目(92158202, 41576015)

[The National Natural Science Foundation of China, Nos. 92158202, 41576015]

高永丽(1981—), 女, 山东胶州人, 汉族, 讲师, 博士, 主要从事非线性最优化、参数敏感性分析方面的教学与研究, E-mail: gaoyongli@upc.edu.cn; 张坤(1988—),通信作者, 男, 山东济宁人, 副研究员, 主要从事海洋环流及其可预报性的研究, E-mail: kzhang@qdio.ac.con

(本文编辑: 杨 悦)