弹性地基梁板的径向基函数逼近求解方法
林军志,杨 笛,徐绩青,3
(1. 重庆交通大学 河海学院,重庆 400074; 2. 山区公路水运交通地质减灾重庆市教委重点实验室,重庆 400074; 3. 重庆交通大学 国家内河航道整治工程技术研究中心 水利水运工程教育部重点实验室,重庆 400074)
0 引 言
在工程中因地基变形而导致建筑物的损坏是不可无视的,因此与土体接触的结构应按弹性地基梁和弹性地基板来考虑。笔者以Winkler模型为基础,假设地基表面任一点的沉降与该点单位面积上的压力成正比,建立了挠度微分方程式和边界条件。
目前针对弹性地基梁板的挠度求解研究成果颇丰,如经典的Navier弹性地基板双三角级数解[1],该方法是将荷载转化为级数形式,将满足边界条件的试函数带回微分方程得到挠度理论解;初参数法[2]是用挠度ω、转角θ、弯矩M、剪力Q代替挠度函数中的4个参数,使积分常数具有明确的物理意义;处理变截面梁和边荷载问题的链杆法[2],是用链杆力代替地基反力;杨维加[3]对弹性地基梁采用三角级数法进行求解;杨成永等[4]针对带有脱空弹性地基梁问题采用傅里叶级数法进行求解。以上解析方法都是针对某些特定条件或规则形状进行的求解,其计算形式较为复杂。
有限元方法在样条函数空间寻找近似解,但对于求解高阶偏微分问题所构造高阶连续样条函数基(高阶连续单元)非常困难,且每次计算都需要剖分网格,计算工作量大。无网格方法[5]主要有滑动最小二乘法[6]、伽辽金法[7]、杂交边界法[8]等,这些方法均是通过数值积分得到弱形式解。基于径向基函数[9-14]的求解具有如下优点:表达与计算非常简单、各向同性、任意多元函数都可用一元函数来描述、节约存储成本、可以逼近几乎所有的从各向同性问题中产生的函数。采用径向基函数,结合加权余量法[15]中的配点法对线性方程组进行离散,通过笛拉克函数控制残差可得到计算简单、精度高、通用性强的强形式解。
1 挠度微分方程与边界条件
1.1 弹性地基梁
域内微分方程的计算如式(1):
(1)
自然边界条件如式(2):
W|x=0,l=0
(2)
本质边界条件如式(3):
(3)
式中:EI为弹性地基梁的弯曲刚度,kN·m;k为弹性地基系数,kN/m3;b取单宽,m;l为宽度,m;q(x)为施加在弹性地基梁上的荷载,kN/m。
1.2 弹性地基板
域内微分方程的计算如式(4):
D∇4W(x,y)+kW(x,y)=q(x,y)
(4)
自然边界条件如式(5):
W|x=0,2a=0,W|y=0,2b=0
(5)
本质边界条件如式(6):
(6)
式中:D为弹性地基板的弯曲刚度,kN·m;2a、2b分别为板的长和宽,m。
2 径向基函数

笔者根据文献[9-10],基于修正再生核逼近思想构造了局部紧支撑径向基函数(该函数使离散插值矩阵具有带疏性)及根据经验改良后的Gauss公式,如式(7)~式(12)。这样可以解决因数值计算中布点过密产生的病态矩阵问题。
φ(r)=(1-r)5×(1+5r+9r2+5r3+r4)
(7)
φ(r)=(1-r)6(6+36r+82r2+72r3+30r4+5r5)
(8)
φ(r)=(1-r)6(3+18r+35r2)
(9)
φ(r)=(1-r)7(5+35r+101r2+147r3+101r4+35r5+5r6)
(10)
φ(r)=(1-r)8(1+8r+25r2+32r3)
(11)
φ(r)=expcr2
(12)
需特别注意,若有r=d/dmax则以上函数应满足式(13)。
(13)
3 径向基函数配点法
3.1 加权余量配点法
已知基本微分方程式和边界条件[15]:
(14)
式中:D、G分别为微分算子;d、g分别为不含函数的项;u为待求函数项;m为边界条件数。
假设待定函数u的近似解为Ui,则有式(15):
(15)
式中:ai为待定系数;fi为形式确定的试函数项;n为试函数项的数目。
将近似解代入微分方程,则有内部残量R1和边界残量R2[15]:
(16)
选用笛拉克函数作为权函数ωi(x),如式(17):
ωi(x)=δ(x-xi)=0,(x≠xi)
(17)
根据笛拉克函数的挑选性,控制残差在一系列配点上xi=0,则有式(18)。
(18)
求解式(18),即可得到待定系数ai。
3.2 径向基函数配点求解
取径向基函数作为试函数,则挠度的近似解Ui[11]可由式(19)表达。
(19)
所求区域用n个节点离散。设P为区域内部nP个节点的集合;Q为边界x方向上的nQ个节点集合;S为边界y方向上的nS个节点集合;则有n=nP+nQ+nS。n个节点对应的未知挠度为n个,试函数数量与未知量数量相同,可建立n个线性方程组,如式(20)。
(20)
令特征矩阵A=[Φ(r)],系数矩阵α=[α1,α2,…,αn]T,待求矩阵U=[U1,U2,…,Un]T,则可简化如式(21):
Aα=U
(21)
任意点的挠度近似解可表示为式(22):
[φ1(ri)φ2(ri) …φn(ri)]A-1U
(22)
梁、板方程的求解〔式(1)~式(6)〕一般分为两种方法。
方法1:不求逆矩阵,以待定系数矩阵α为未知量求解。
方法2:求逆矩阵,以待求矩阵U作为未知量求解。

3.3 方法改进
在数值计算中,常规配点法往往会在边界处产生严重振荡[14],针对这一问题可利用本质边界条件新增未知量,借鉴弹塑性静力学的处理方法提出n个节点挠度和nQ+nS个边界点挠度的二阶偏导量联合插值的近似解,如式(23),明确附加了未知量的物理意义。
(23)
式(23)对于径向基函数的高阶连续性有一定要求,为了避免径向基函数高阶求导后形成的特征矩阵条件数增大,应对式(23)进行简化。
分别采用线性无关的辅助径向基函数βi(ri),γi(ri)来代替高阶偏导项,如式(24)。
(24)
式(24)中:右边第1项代表n个节点的挠度;第2项代表在边界点上对x方向的曲率;第3项代表在边界点上对y方向的曲率。
此时式(24)可写作式(25):
(25)
n+nQ+nS个待定系数的n个方程组为超定解,因此为满足一一对应关系,构造了附加未知量、矩阵A的附加行。数值计算中为降低方程组求解难度,从减小误差思想出发,构建附加未知量与本质边界条件等价可以使方程组的附加行列成为类单位阵。改造后的矩阵A及待求矩阵U如式(26)、 式(27):
n个节点对应n+nQ+nS个未知数,建立了n+nQ+nS个线性方程组,其中Vi,Zi为附加未知量。Vi表示为边界点在x方向上挠度二阶偏导量,即x方向的曲率;Zi表示为边界点在y方向上挠度二阶偏导量,即y方向的曲率。得到的近似解如式(28):
(26)
U=[U1…UnV1…VnQZ1…ZnS]T
(27)
[φ1(ri) …φn(ri)β1(ri) …βnQ(ri)γ1(ri) …γnS(ri)]A-1U
(28)
4 算法实施
1)建立4阶偏微分方程和边界条件方程;
2)在规定区域合理均匀配点,并求得个节点之间的距离及其影响半径;
3)选取各线性无关的径向基函数作为主函数和辅助函数构造近似解Ui;
4)方法1:根据各节点位置结合边界条件构造特征矩阵A使得附加未知量具有物理意义;
方法2:根据各节点位置结合边界条件构造特征矩阵A,使得附加未知量具有物理意义并求得逆矩阵B=A-1;
5)对近似解Ui求4阶偏导;
6)方法1:将近似解Ui和4阶偏导带入微分方程中,并针对边界点改变该行的微分方程使其满足自然边界条件。显然具有公因子[a1, …,anb1, …,bnQc1,…,cnS]T;
方法2:将近似解和4阶偏导函数带入微分方程中,并通过化零置一的方法使其满足自然边界条件。显然具有公因子[U1, …,UnV1, …,VnQZ1,…,ZnS]T;
7)方法1:利用A附加行的意义构造方程组,满足微分方程和本质边界条件;
方法2:由于附加未知量与本质边界条件等价,因此在联立方程时,式(3)、式(5)无需再次计算2阶偏导式,而是构建类单位阵满足边界条件。若以第一个边界点x方向曲率为例,如式(29):
(29)
转换为式(30):
(30)
8)方法1:联立方程组求得未知系数并带回式(24),求得近似解Ui;
方法2:联立方程组直接求得未知量Ui。
5 算例分析
5.1 弹性地基梁的挠度分析
算例1:假设一个两端简支的弹性地基梁,受均布荷载作用q=2 kN/m;简支梁长度为L=4 m;EI=2.5×106kN·m2;地基弹性系数k=4×104kN/m3。如图1。

图1 弹性地基梁受均布荷载Fig. 1 Elastic foundation beam subjected to uniformly distributed load
已知弹性地基梁的挠度微分方程与边界条件为式(1)~式(3),可得到理论解,如式(31):
(31)

(32)
(33)
则无量纲挠度理论解如式(34):
(34)
利用径向基函数配点逼近的方法进行求解,选用文献[10]提出的一维6阶连续函数作为主函数和一维4阶连续函数作为辅助函数。一维梁结构不存在y方向的曲率,因此构造出近似解Ui和矩阵A。
取节点间距为0.05均匀布点,则一共有n=21个节点,其中两个边界点nQ=2。采用方法一直接联立式(1)~式(3),求解得到未知系数代入近似解的挠度值如图2。从数学精度方面考虑全局相对误差1.38%;工程上为满足安全性原则,一般考虑最大挠度变形点。由图2可见:最大挠度变形发生在跨中0.012 5 m处,与理论解相比,其相对误差仅为0.084%,优于最小滑动二乘解。

图2 弹性地基梁受均布荷载挠度分析Fig. 2 Deflection analysis of elastic foundation beam subjected to the uniformly distributed load
5.2 弹性地基板的挠度分析
5.2.1 算例2
若有一块简支弹性地基板,板长为10 m(即a=5),板宽为10 m(即b=5);板的弯曲刚度为D=2.5×104kN·m;地基弹性系数为k=104kN/m3;板上受到均布荷载为q=2 kN/m2,如图3。

图3 弹性地基板受均布荷载Fig. 3 Elastic foundation beam and plate subjected to the uniformly distributed load
已知弹性地基板的挠度微分方程与边界条件为式(4)~式(6),则可得到理论解,如式(35):
(35)
利用径向基函数配点逼近的方法进行求解,选用文献[10]提出的三维4阶连续函数作为主函数,文献[9]构造的三维4阶连续函数作为辅助函数和文献[10]的三维6阶连续函数作为辅助函数构造出近似解Ui和矩阵A。
板面上4个角点同时考虑对x、y两个方向求曲率,利用方法2求出逆矩阵B,利用附加未知量的意义构造一个类似单位矩阵的大小为2m行n+2m列的矩阵M(M=[RT]),R为2m行n列的零矩阵,T为2m行2m列的单位矩阵。使其乘以n+2m个未知量,并通过化零置一转化成未知系数与本质边界条件等价的未知量。取节点间距为0.25,均匀布点,则一共有n=1 681个节点,其中边界点160个。
得到的各挠度值如图4。
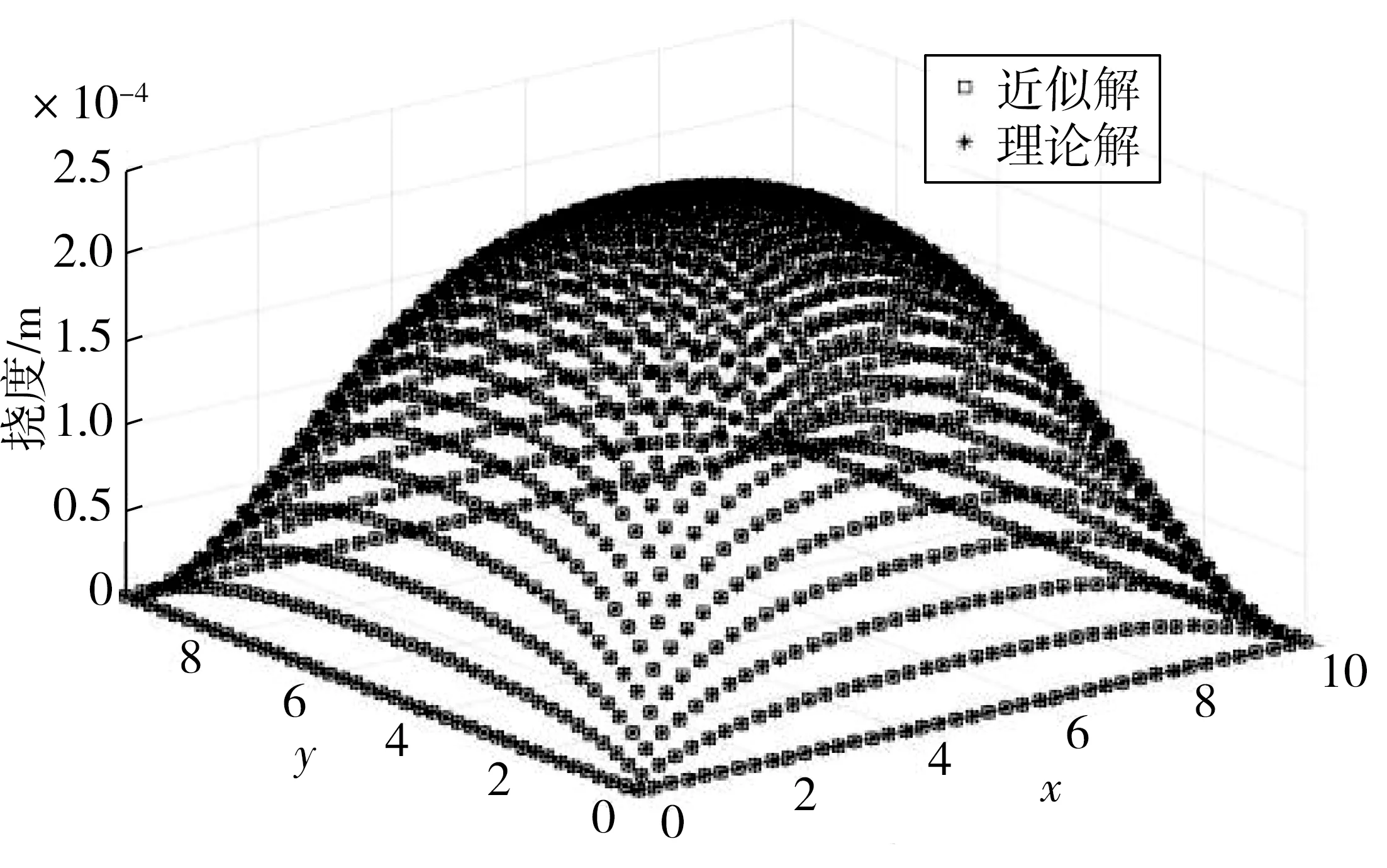
图4 弹性地基板受到均布荷载的挠度分析Fig. 4 Deflection analysis of elastic foundation beam and plate subjected to the uniformly distributed load
板最大挠度变形发生在板中央,近似解为2.42×10-4m,略大于理论解,挠度最大值相对误差为0.012%。此时逆矩阵的求逆精度为3.05×10-5,从工程实际而言效果较好;节点全局平均相对误差为0.46%,从数学层面考虑精度较好。
5.2.2 算例3
若有一块四边简支的正方形薄板,几何尺寸为1 m×1 m(即a=0.5,b=0.5)。板的弹性模量为E=2.1×1010Pa,泊松比为μ=0.3,地基弹性系数为k=4.9×104kN/m3,板上受到均布荷载为q=1 kN/m2。
利用径向基函数配点逼近方法进行求解,选用改良后的Gauss函数作为主函数,辅助函数为式(8)、 式(9)分别对x、y方向的曲率。在满足域内微分方程和边界条件的情况下构造出近似解Ui,采用方法二求逆矩阵B,并以待求矩阵U作为未知量建立方程组。
取节点间距为0.025,共有n=1 681个节点,其中160个边界点。由于地基反力变大,挠度最大值不会发生在板中央,由此得到挠度结果[7],见图5。与理论解对比,挠度最大值相对误差为0.178%,与整体相对误差严重不匹配,这是因为Gauss函数求逆精度低。

图5 马鞍形挠度值(调整前)Fig. 5 Saddle-type deflection value (before the adjustment)
故从代数方面考虑,让边界点除了满足边界条件外同时满足边界微分方程,如式(36),通过改变矩阵大小及排列来提高精度。
(36)
主函数与辅助函数不变,此时x、y两个方向的曲率都用式(8)表示,4阶偏导用式(9)表示,构造出近似解Ui和矩阵A如式(37)、式(38),其余步骤与方法2相同。
(37)
(38)
调整后的挠度值如图6。与理论解对比,其整体相对误差明显减小,挠度最大值的相对误差为0.013%,比调整前提高10倍,精度满足工程需要;板中心挠度相对误差为0.013 5%,与杂交边界法相当。

图6 马鞍形挠度值(调整后)Fig. 6 Saddle-type deflection value (after the adjustment)
6 结 论
笔者为求解弹性地基梁和弹性地基板的挠度值,采用了径向基函数配点逼近的方法,得出如下结论:
1)径向基函数配点法形式简单,无网格化,计算方便,求解精度高;
2)在构建矩阵A时,可根据边界条件编写附加行,使得附加未知量具有一定的物理意义,从而通过简化方程求解来减小误差;
3)针对方程求解提出两种算法:不求逆矩阵,以待定系数作为未知数进行求解;求逆矩阵,以挠度值作为未知数进行求解,根据矩阵求逆精度选择算法;
4)参考紧支柱思想,改造了与全局支撑域相关联的Gauss函数,使其无量纲化,根据经验确定其参数c=-23.026;
5)为解决改造后的Gauss函数求逆性差的问题,可利用边界微分方程建立辅助函数,以提高求解精度。

