基于稀疏数据的流场结构重构方法研究

陈旷奇，欧阳晗青，朱志成，郝佳，黄彪

（北京理工大学 机械与车辆学院，北京 100081）

高精度和高可信度的流场数据往往伴随着高昂的时间成本与经济成本，以直接数值模拟(DNS)为例，虽然它对湍流流场的求解精度得到了学术界的广泛认可，并且已经有了初步应用，但网格数量至少需要能达到基本的计算要求，而急剧增加的网格数量严重限制了其应用范围.与此同时，流体实验所得的有限数据也无法提供更为精细的流场结构,在相关气/水动工程问题中，研究者往往需要根据有限实验数据反复迭代，不仅主观因素强，而且成本极高，极大地制约了研究效率.与此同时，流动条件愈加复杂，仅通过数值模拟或实验测量获得高精度数据也更加困难，因此，亟需一种数据挖掘手段，可以从有限数据中获得所需的研究信息.

机器学习技术作为数据挖掘的重要手段，近年展现出巨大的潜力，而深度学习便是其重要分支，能够在海量数据中自动提取并学习最优特征，在图像识别[1]、自然语言理解[2]、认知科学[3]，网络漏洞分析[4-5]和基因组学[6]等多领域中已取得突破性进展，逐渐在各类基础研究和工程技术中发挥不可替代的作用.目前已有学者尝试将机器学习技术应用于流体力学中，在湍流建模[7]、主动流体控制[8]、流场特征识别[9]以及多相流流态识别[10]上都有着突破性成果.传统机器学习方法主要以数据驱动为主，通过神经网络拟合输入和输出间的映射关系.这种方法实际上是从已知的信息源中寻找信息，因此对数据的数量和质量有着较高的要求.与此同时，数据驱动型神经网络将数据样本作为单一信息源，必然导致其对高质量数据集的过度依赖，这也是阻碍机器学习应用于流体力学的重要原因.

流体力学研究以数理模型为主，积累了丰富的理论基础，但这些信息尚未被数据驱动型神经网络利用.将已有的物理模型作为高精度数据的补充融入神经网络，是深度学习技术与流体力学领域交叉融合的关键基础.随着物理信息驱动型神经网络框架(physics-informed neural networks，PINN)[11]被提出，数据驱动型神经网络缺乏可解释性且极度依赖高质量数据集的现状得到改善，立刻受到学术界的极大重视，在短时间内出现了大量以PINN 框架为基础的理论研究，例如非局部型PINN：nPINNs[12]、分数阶PINN：fPINNs[13]等.在流体力学领域，已有不少学者开始将PINN 框架应用到具体流动问题中.RAISSI等[14]基于PINN 框架提出了隐式流体力学（hidden fluid mechanics，HFM），仅利用少于1%的烟雾浓度测量数据，便重构出全部流场，并通过与数值计算结果对比证实了该方法不受边界形状的限制，在保证精度的同时，有着远快于数值模拟的求解速度.EIVAZI等[15]将PINN 框架应用于湍流求解，提出利用数据封闭雷诺平均方程，不需要任何湍流模型或假设即可求解雷诺平均方程.MAO 等[16]证实了利用PINN 框架近似模拟高速气动力学中Euler 方程的可行性.同时建立了PINNs 方法，当求解域中存在高梯度区域时，将其划分为若干子域，并对每一个子域独立使用神经网络，可以提高求解精度.对于流体中的正问题，PINNs 的计算精度不如传统的数值方法，但对于传统数值计算方法无法求解的反问题，PINNs 更具有优越性.GAO 等[17]将PINN 的思想引入到卷积神经网络，提出基于物理信息的DL-SR 方法，利用流体流动守恒定律和边界条件从高维参数空间的低分辨率数据中产生成超分辨流场.CHENG 等[18]在PINN 框架的基础上提出了Res-PINN 模型，通过将Resent 模块与神经网络耦合进一步增强了深度学习的预测能力，可以精准预测流场中的速度和压力信息.同时，也可以应用在流体的反问题中，反演参数的误差为0.98%和3.1%；在噪声数据中，反演参数的误差仅有0.99%和3.1%.ALMAJID 等[19]利用PINN 框架预测多孔介质流体流动.通过融合物理信息和观测数据来模拟Buckley-Leverett 问题，并通过神经网络反向求解，推导出最符合实验结果的多相流参数.结果表明，即使没有观测数据，PINNs 也能捕捉到解的整体趋势，但随着观测数据的增加，解的分辨率和精度都有很大提高.

文中首先建立了一种基于边界数据浸入法的数值模拟方法，并把求解结果作为神经网络的高精度数据集, 然后基于PINN 框架构建了耦合流场物理信息的神经网络模型，发展了圆柱绕流流场的数据采样方法和神经网络模型优化策略，基于稀疏流场数据建立了物理信息驱动的流场结构重构方法.通过分析重构流场的水动力特性与涡脱落特性揭示了物理信息驱动型神经网络的预测误差机理.对比不同流态的绕流流场，讨论了该神经网络模型对不同流场结构的预测能力.

1 数据集的准备

高质量数据集是训练神经网络模型的必要保证，对最终预测效果的影响甚至远远超过算法本身.文中基于Fortran 自编程求解了圆柱绕流流场结构，通过两步投影法结合泊松方程解耦N-S 方程，同时通过边界数据浸入法（boundary data immersion method，BDIM）处理固/液边界，为后续神经网络提供了高置信度的数据集.

1.1 基本控制方程

本节的研究对象刚性圆柱绕流流场，同时忽视了自由表面对模型附近流动影响的圆柱绕流，计算中涉及到的介质均为不可压缩流体.因此流动控制方程为

①连续性方程：

②动量方程：

式 中： →u和p分 别 为 流 场 的 速 度 和 压 力； ρ 和 µ分 别 为流 体 的 密 度 和 动 力 黏 性 系 数； →g为 重力加速度； ∇为梯度运算符.

1.2 求解方法

文中通过Chorin 投影法求解N-S 方程组，同时采用边界数据浸入法（BDIM）处理固/液边界，关于Chorin 投影法和边界数据浸入法的详细推导过程，可以见文献[20]和[21].图1 展示了利用二步投影法和边界数据浸入法求解不可压N-S 方程的具体过程.

图1 不可压缩N-S 方程求解流程图Fig.1 Flow chart of solving incompressible N-S equation

1.3 计算域及边界条件设置

本算例是基于Fortran 自编程求解，流场计算域及边界条件设置如图2 所示，计算域建立在笛卡尔坐标系中，其中x代表顺流方向.以圆柱体的直径D=0.064 m 为特征长度，计算域选取在长24D、宽5D、高5D的矩形流域内.计算采用入口速度条件，出口压力条件设置，圆柱体的中轴线距离入口边界和出口边界分别为2.5D和12D，与上下边界的距离为2.5D，入口边界的距离为2.5D.

图2 计算域和边界条件设置Fig.2 Calculation domain and boundary condition setting

在文中的数值计算中,液体的密度和动力黏度分别取ρg=997 kg/m3，μg=10-3Pa·s.25 °C 下，饱和蒸汽压取pv=3 169 Pa，出口处压力设为p0=43 169 Pa.

在本算例中采用高分辨率的精细化均布网格，在节省计算资源的同时，尽可能多地捕捉流场流动细节，提高计算精度.文中针对工况Re=100 000，参考其他学者的实验结果(Cd=1.25，St=0.19)[20-22]，采用表1所示的四组不同尺度网格对圆柱的平均阻力系数和斯特劳哈尔书进行了对比计算.

表1 网格参数设置及独立性检验Tab.1 Mesh parameter setting and independence verification.

从结果可以看出，随着总节点数的增加，平均阻力系数逐渐收敛于试验结果，并且网格3 和网格4的结果非常相似.综合考虑计算精度和计算资源，网格3 较为合理，将在本研究中使用.

为了探讨PINN 框架对不同流态流场的重构能力，文中分别计算了雷诺数Re=100，3 900，20 000 和100 000 四种工况，同时与其他学者实验结果进行对比，结果如表2 和表3 所示.

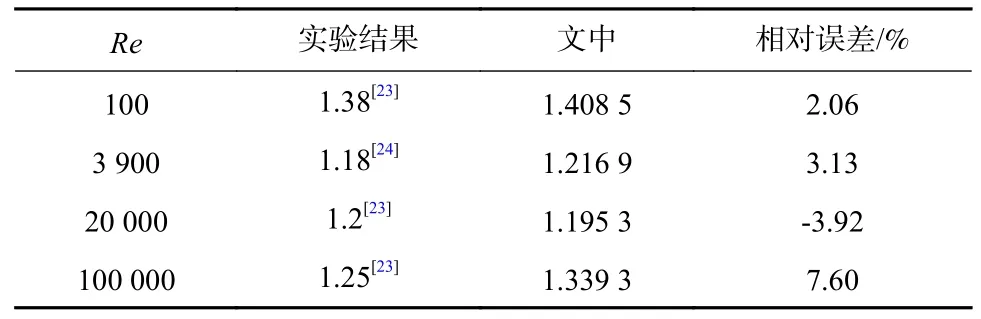
表2 平均阻力系数对比Tab.2 Comparison of average resistance coefficient

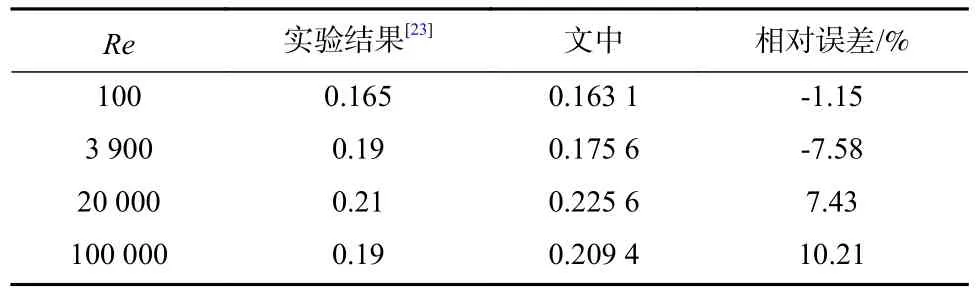
表3 斯特劳哈尔数对比Tab.3 Comparison of Strouhal numbers.

文中对比了不同雷诺数下平均阻力系数对比与斯特劳哈尔数，并且对比了Re=3 900 工况下时均流速的实验数据[22],可以看出，文中的数值计算方法在中低雷诺数下具有较高的精度.

如图3 所示，平均阻力系数，斯特劳哈尔数以及时均流速均与实验吻合较好，因此可以认为文中数值计算方法提供的数据集真实.

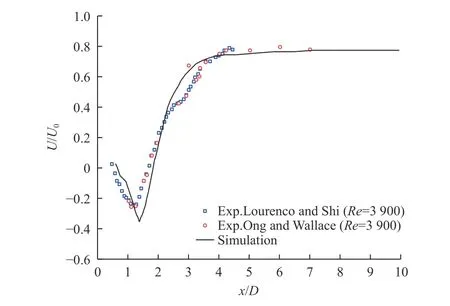
图3 轴向中心线上沿流动方向的时均流速分布对比（Re=3 900）Fig.3 Comparison of time-averaged velocity distribution along the flow direction on the axial centerline (Re=3 900)

2 神经网络模型搭建与训练

PINN 框架将物理信息与神经网络结合，通过补充物理机理便可使基于稀疏数据的神经网络收敛.该框架耦合物理信息的基本原理是：基于物理方程构造方程项残差并与数据项损失函数加权，最终统一为神经网络的损失函数.随着网络参数的迭代优化，损失函数值逐渐减小至预定精度，本质上是对控制方程的求解.该技术与求解偏微分方程的变分方法相似，不同之处在于使用深度神经网络模型作为试函数，利用机器学习方法进行权重的迭代更新.

2.1 稀疏数据采样

在流场数值模拟中，每一个网格节点均代表一个数据点，考虑到圆柱绕流流场的周期性，仅在计算域中选取图4 所示虚线区域作为重构区域，三个方向均是等比例均匀采点，数据点个数为240×100×100=2 400 000.以数值模拟一个时间步为一个单位，间隔选取流动稳定后的50 个时间步用于训练.

图4 神经网络重构区域Fig.4 Areas reconstructed by neural network.

物理机理地引入使得神经网络仅利用稀疏数据便可实现网络收敛.考虑到实验中数据获取的合理性，文中将数值计算的部分速度数据和圆柱表面压力数据作为神经网络的训练数据.流场速度数据如图5 所示.

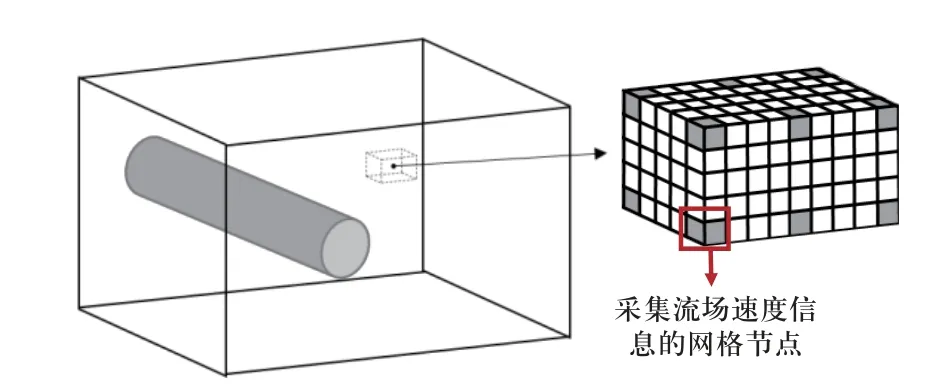
图5 速度数据采样方式Fig.5 Sampling method of velocity data

图中灰色区域代表采样点，x和y方向均采集数据点的1/4，最终流场采样数据点为60×25×25=37 500；压力数据采样也采用等间隔采样方式，由于液体的黏性，固体表面的速度理论上为0，但由于边界数据浸入法会使圆柱表面存在一个图6 所示的过渡区域.为了保证预测的准确性，文中只将图6 所示的边界压力数据代入神经网络.

圆柱表面节点的采样方式如图7 所示.在周向和轴向方向上均采用均匀间隔采样，最终界面采点数量为30×15=450.

图7 压力数据采样方式Fig.7 Sampling method of pressure data

综上，在固定时间步下，文中从流场中采样数据如表4 所示.

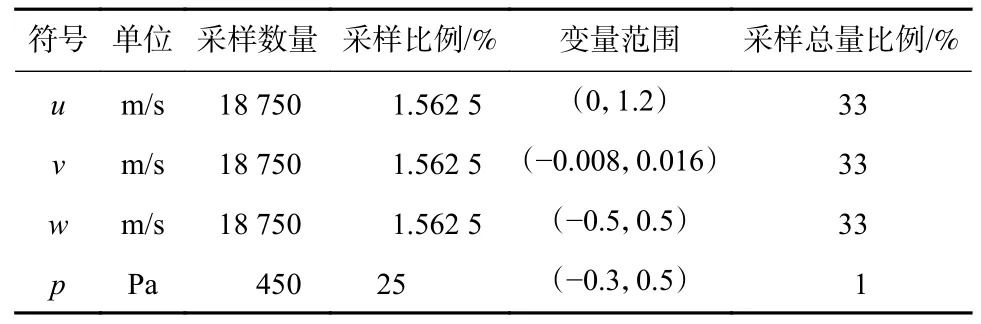
表4 固定时间步下采样数据汇总Tab.4 Sampling data summary under fixed time step

在PINN 框架中各物理变量需要代入方程求解方程残差，由于min-max 标准化或Z-score 标准化会破坏变量之间的量纲关系，因此文中仅对数据仅进行无量纲化处理，处理式为

式中：u，p和x分别为有量纲的速度，压力和长度；u*，p*和x*分别为无量纲的速度，压力和长度（下标i分别为x,y,z三个方向），分别被来流速度u0、圆柱直径D和流体密度ρ无量纲化.

2.2 神经网络构建与训练方法

基于PINN 框架，文中通过耦合流动机理得到如图8 的物理信息驱动型神经网络模型.

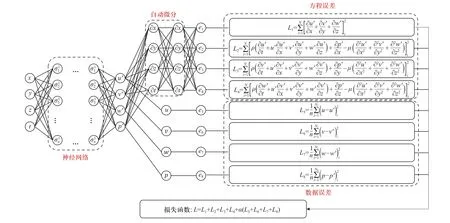
图8 神经网络结构Fig.8 Architectures of neural network

该模型将时空信息（即流场位置坐标与时间）作为神经网络的输入，通过神经网络计算流场各物理量，包括三个方向的速度和压力.首先，将神经网络的输出流场结构信息{u,v,w,p}与其标签信息{x,y,z,t}共同带入偏微分方程，通过自动微分技术求得方程误差.方程误差包括质量方程误差L1和动量方程误差L2、L3、L4，分别为

式中：x,y,z,t为样本的标签物理量，文中指样本点的时空坐标(x,y,z,t)；u,v,w,p为神经网络的输入数据集，分别为流向速度u、法向速度v、垂向速度w、流场压力p；u',v',w',p':神经网络的输出数据集，分别代表预测流向速度u'、法向速度v'、垂向速度w'、流场压力p';N: 神经网络的输入样本点总量；i为第i个样本数据的对应编号.之后求解神经网络的输出流场信息{u',v',w',p'}与该时空坐标下已知信息{u,v,w,p}间的误差，基于本算例的采样情况，该误差分为流域速度误差L5、L6、L7与边界压力误差L8，其计算式为

①流域速度误差

②边界压力误差

式中：Nl为输入神经网络的流域样本点总量；Nb为输入神经网络的边界样本点总量；u,v,w,p为采样点的流场信息.

将两种误差相加，并通过平衡权重α调整数据误差在总误差中所占的比例，即可得到神经网络的损失函数

从表2 中可以看出，速度v量级远小于速度u,w，这是由于本算例的研究对象的是在轴线方向上没有曲率变化的光滑圆柱.从表2 中可以看出，增大速度v的量级相比于其他变量过小，因此为了增大速度v对神经网络权重更新的影响，文中对速度v的数据误差乘以修正权重100，使其与速度u，速度w处于同一量级，因此神经网络损失函数为

通过神经网络的反向传播与梯度下降算法最小化损失函数，更新神经网络中的权重，直至神经网络收敛.综合上述内容，神经网络的训练流程如图9所示.

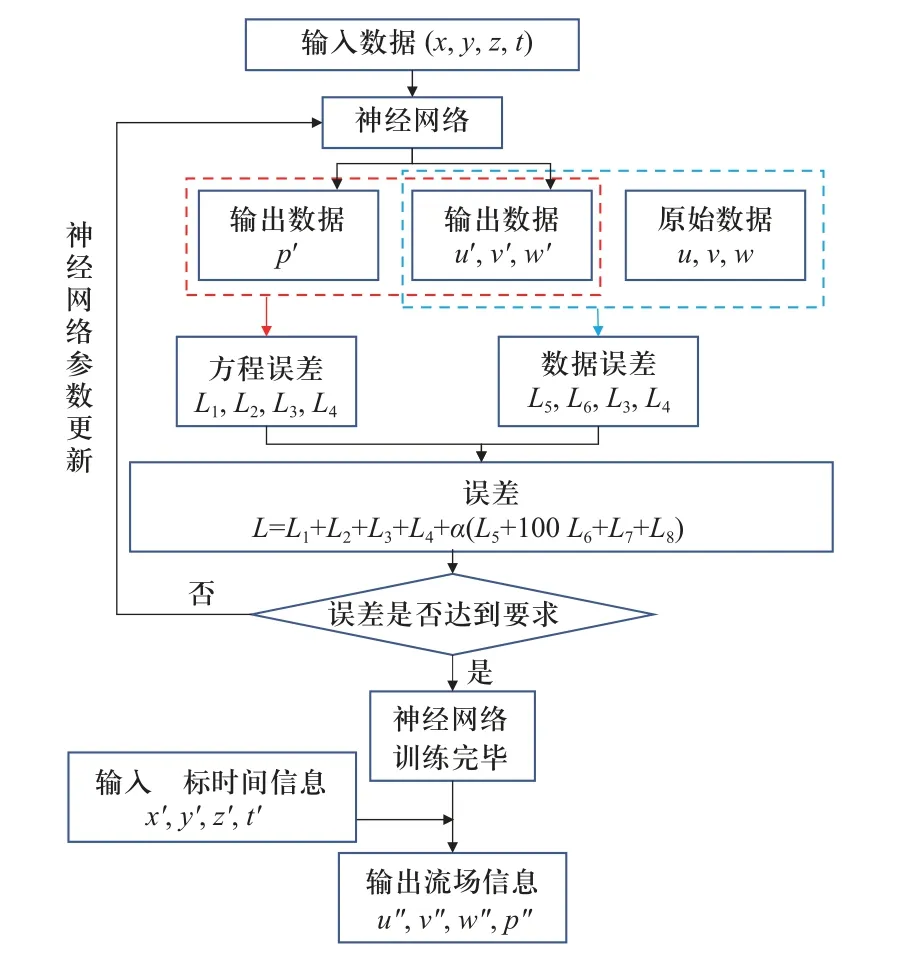
图9 神经网络训练流程图Fig.9 Flow chart of neural network training

文中神经网络基于全连接神经网络搭建，包含10 个隐藏层，每层包含500 个神经元.本次训练采用了Adam 优化器，学习率设为10-3，预设训练时间为40h，微分的计算由tensorflow 中的自动微分完成.激活函数选取sigmoid 函数.

2.3 神经网络权重选择

文中首先以雷诺数Re=3 900 工况为例，为了便于误差分析，文中将神经网络损失函数分4 部分输出，分别为基于流场数据的流场误差loss1；基于表面压力数据的界面误差loss2；基于物理方程的方程误差loss3以及三项误差之和的总误差loss_all，其计算式为

流域误差loss1:

界面误差loss2:

方程误差loss3:

其中，L1至L7的计算方式见式(4)～(5).

为了确定平衡权重α的最佳取值，文中首先将α取1，即数据项和方程项对神经网络权重更新的影响比例相同，此时流域误差为loss1=L5+L6+L7.图10 为α=1 时神经网络四类误差随训练轮数（epoch）的输出曲线可以看出，四项误差均随着迭代次数的增加而明显减小.方程误差loss3的最终收敛数值在3 类误差（不包括总误差）中最大，稳定在10-4.2左右，此时方程误差对总误差的影响较大，导致在迭代过程中，神经网络很难从数据项中获得训练信息.因此通过增大损失函数中平衡权重系数α增大流域误差对神经网络训练的影响.对于权重的选择参考文献[25]结果，文中重点关注α取1，100，300，500 这几种情况，其中方程误差曲线如图11 所示.

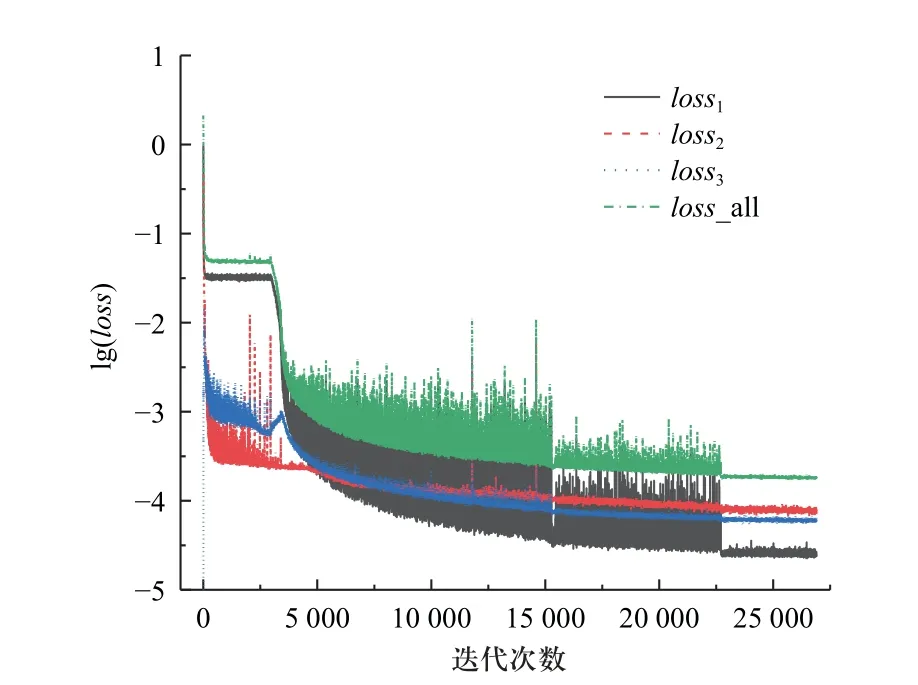
图10 神经网络误差输出曲线（α=1）Fig.10 Error output curve of neural network (α=1)

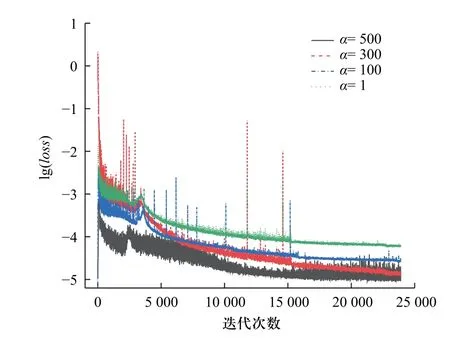
图11 不同权重系数下神经网络误差曲线对比图Fig.11 Comparison of neural network error curves under different weight coefficients

可以看出，随着权重系数的不断增大，方程误差的收敛值在逐渐降低，当权重等于300 和500 时，方程误差收敛值均为10-4.9.不同点在于α=500 时误差曲线波动较大稳定性较差.

为了进一步验证权重系数对预测精度的影响，在图4 所示的流场区域中随机选取100 个点，计算在各个权重系数下流场各变量与真实值之间的平均相对误差，最终结果见表5.

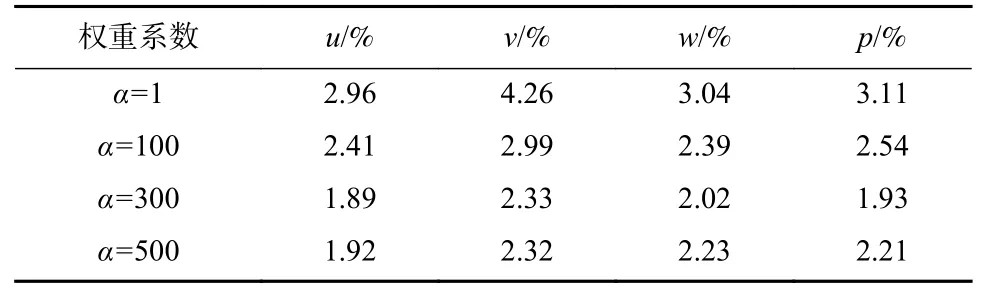
表5 各权重系数下流场变量预测平均相对误差Tab.5 The prediction average relative error of flow field variables under each weight coefficient

可以看出，随着α从1 增加到500，速度v相对误差下降明显，考虑α=500 时误差曲线有明显波动，因此平衡权重α的取300 最合适.

3 预测结果分析

图12 展示了圆柱轴向中心平面上神经网络重构结果.从训练数据中选取第500 步，t=12.35s 的数值模拟结果（此时间步下的流场数据并不参与神经网络的训练过程过程），结果均已无量纲化处理.

图12 神经网络重构结果对比（t=12.35 s）Fig.12 Comparison of prediction results of neural network (t=12.35 s)

为了定量表示神经网络的重构误差，图12(c)给出了相对误差云图.其计算方法为

式中：α为流场中的变量；i为第i个样本点对应编号.可以看出，神经网络重构流场与数值模拟结果吻合度较高.

图13 给出了数值模拟和神经网络重构流场的速度u局部流线图，可以看出神经网络可以精准捕捉流场流动方向.

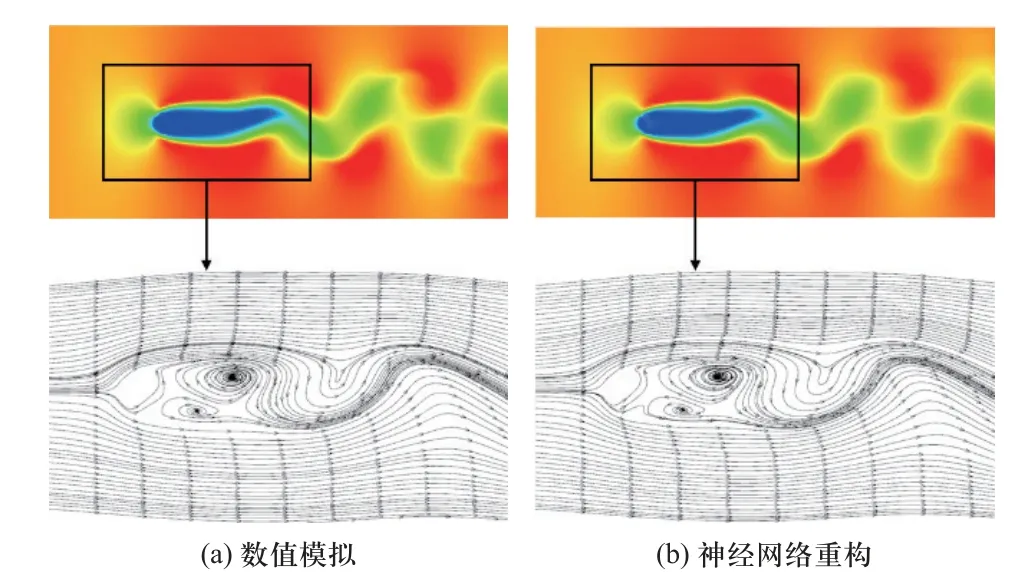
图13 uNS 和uPINN 局部流线图对比Fig.13 Comparison of local streamlines of uNS and uPINN

图14 为神经网络重构流场的升阻力系数变化对比图.可以看出，神经网络重构结果仅能较好地吻合升阻力系数变化周期，这与神经网络训练时参与的数据有关.文中选取50%的稀疏时间参与训练，可以充分体现出各变量的周期变化规律.但由于文中采用边界数据浸入法处理固/液表面，难以获得准确数据，导致神经网络难准捕捉涡的初生与脱落位置.

图14 升阻力系数对比Fig.14 Comparison of lift and drag coefficients

表6 为神经网络重构流场两个周期内的涡量变图，其中tref=10 s.可以看出，神经网络能精准捕捉涡的初生与脱落位置.在图中用两条虚线标注出一个正漩涡从初生到脱落的完整阶段，可以看出在二者结果中，涡核脱落频率和运动速度大致相等.

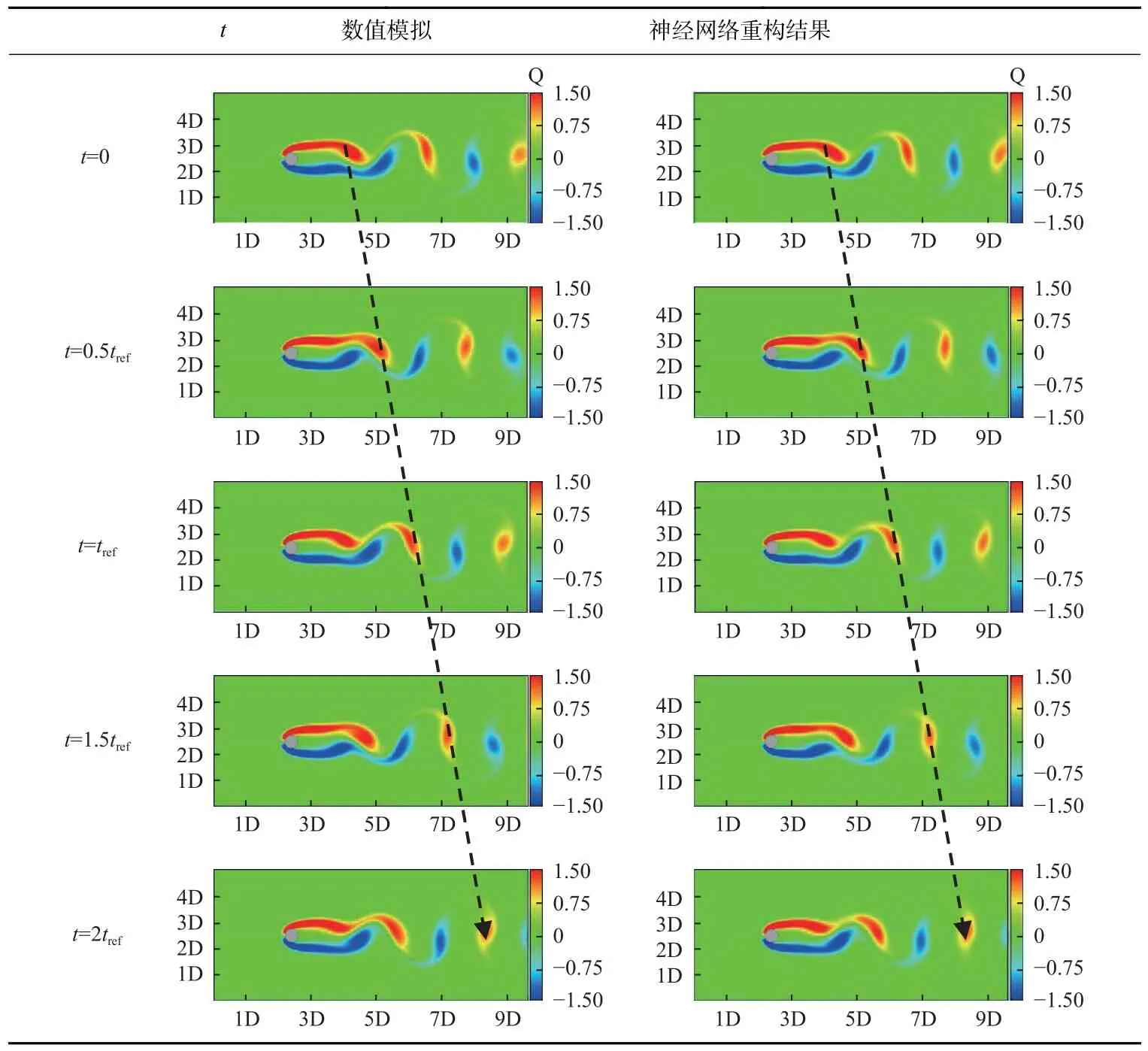
表6 尾涡演化预测对比（Re=100）Tab.6 Comparison of tail vortex evolution prediction (Re = 100)

为了精准对比神经网络对涡量的预测精度，图15为t=0.5tref时刻涡量相对误差云图.可以看出涡量误差集中的区域也呈现出一定规律性，集中在速度变化剧烈的旋涡结构附近，分别为红色区域的高误差区①，相对误差最高可以达到30%左右.灰色区域的低误差区②，③，④，相对误差最高在15%左右.高误差区位于正漩涡的涡脱落位置和反漩涡的初生位置之间，并且越靠近中心位置，误差越大.低误差区位于正漩涡和反漩涡中间.结合图16 的涡量等值线图可以看出，在高误差区，等值线密集，涡量梯度下降最快，在低误差区，涡量趋近于0.高误差区和低误差区的存在，和物理信息驱动型神经网络的拟合方式有关，一方面，神经网络的数据项与正则化项在训练过程中会相互干扰，当正则化项梯度过大时，神经网络会忽略数据项的信息，从而难以拟合微分方程的特解.另一方面，在低误差区中，涡量的变化梯度趋近于0 且数值较小，越靠近两涡中心位置涡量的数值就越小，给神经网络的预测带来困难，因此误差较大.但总体来看，除了大梯度变化区域，神经网络可以较为准确地预测流场涡量变化.

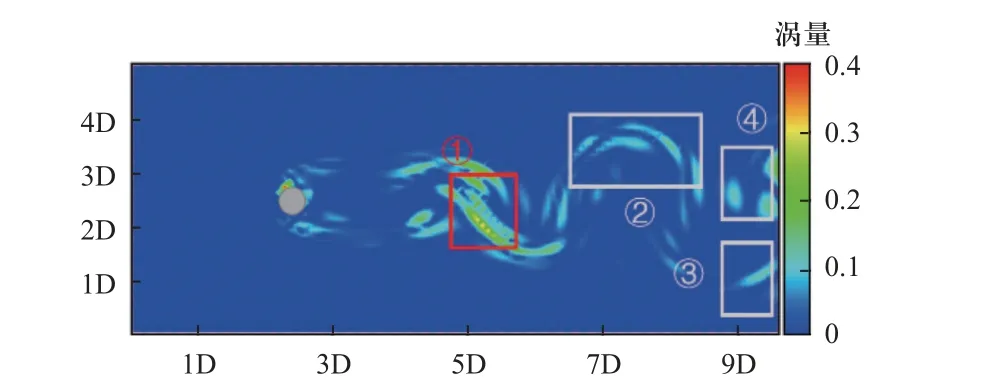
图15 t=0.5 tref 涡量相对误差云图Fig.15 Relative error cloud chart of vorticity (t=0.5tref)

图16 t=0.5 tref 数值模拟二维涡量等值线图Fig.16 Numerical simulation of two-dimensional vorticity contour map(t=0.5 tref)

为了进一步观察重构流场中的涡结构，图17 给出了基于准则下的涡识别图.可以看出，数值方法和神经网络对涡管中心位置的捕捉几乎相同，但神经网络存在部分特征丢失.

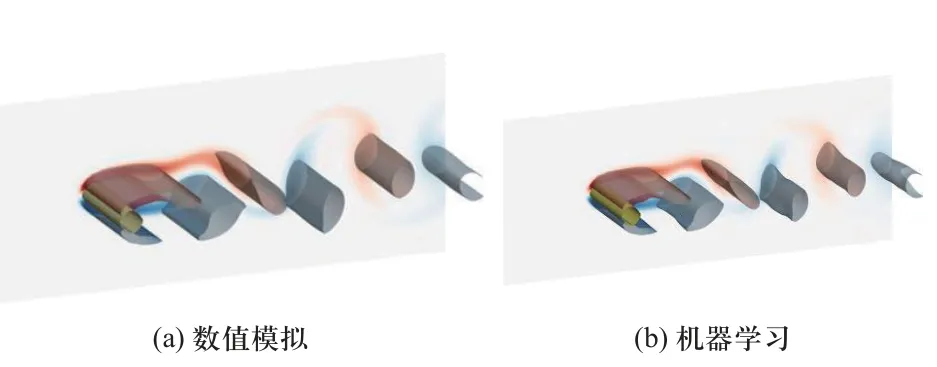
图17 涡结构对比图（Q=0.2）Fig.17 Comparison of Vortex Structure (Q=0.2)

为探讨神经网络对不同流态流场的重构能力，文中分别取雷诺数为100，3 900，20 000，100 000 四种工况，尾涡对应4 种不同的脱落状态，分别为初始脱落，稳定脱落，向湍流过渡的亚稳定脱落以及发展成湍流的不稳定脱落，下图为不同雷诺数下神经网络重构流场的涡量对比结果如表7 所示.

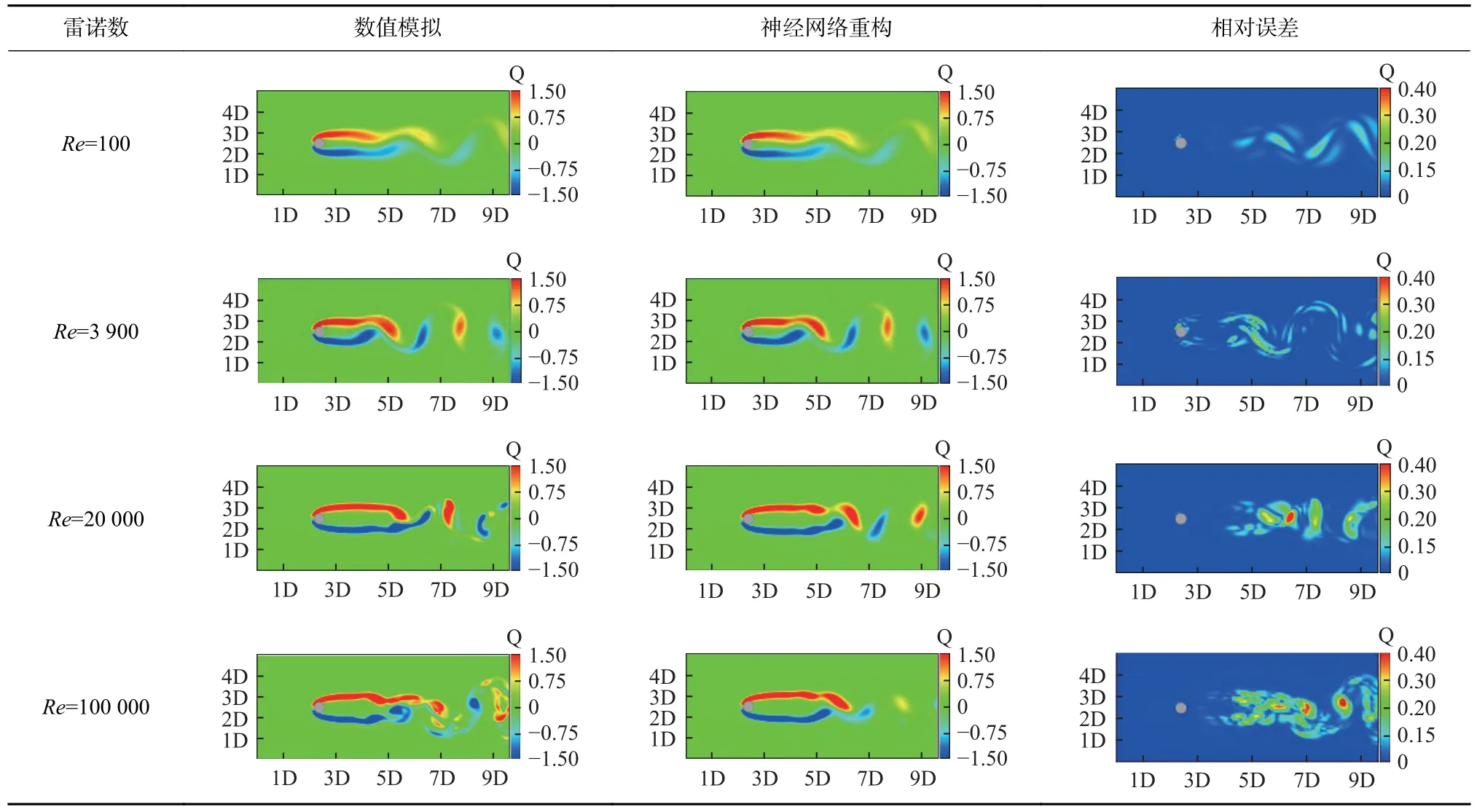
表7 不同雷诺数下二维涡量对比图Tab.7 Comparison of two-dimensional vorticity at different Reynolds numbers

当雷诺数Re=100 时，雷诺数很小，首次产生涡脱落现象，但是漩涡范围较小.可以看出，神经网络对涡量的重构结果与数值模拟基本一致，其中包括漩涡的中心位置，脱落位置以及漩涡的长度.当雷诺数增加到Re=20 000 时，流场处于临界流态，尾涡开始逐渐表现出非定常特性，流动较为紊乱，脱落频率和涡的长度不再固定，同时在流场中开始出现小尺度的离散涡.神经网络的重构结果显示，物理信息驱动型神经网络在此流态下已无法精准重构流场涡的大小以及涡核的位置，高误差区的预测相对误差甚至高达40%左右.当雷诺数增加至Re=100 000 时，此时圆柱尾流完全演变为湍流，流场处于跨临界流态.尾涡以大量的小尺度和离散涡为主，绕流极为凌乱、不规则，此时流场表现出强非线性性和随机性，使得神经网络重构精度进一步下降.在前文中已经论述，神经网络无法捕捉到流场中的小尺度涡结构，而在此流态下流场以小尺度涡为主，因此当雷诺数Re=100 000 时，神经网络的预测结果中没有太多明显的涡结构.对比四种流态下的结果可以看出，当雷诺数增大时，由于涡结构逐渐细小化和离散化，导致神经网络重构精度逐渐降低.为了展示神经网络在雷诺数Re=20 000 和Re=100 000 两种工况下对涡结构的精细捕捉，采用Q准则对两种工况下的涡结构进行识别，如图18 所示.

图18 不同流态下神经网络预测流场涡结构对比（Q 准则）Fig.18 Comparison of vortex structure predicted by neural network under different flow regimes(Q criterion)

可以看出，Re=20 000 和Re=100 000 两种工况下，数值模拟结果中流场的多尺度效应明显， 神经网络虽然无法捕捉小尺度涡结构，但是却可以预测出图中已由黑色虚线框标出的大尺度涡的位置和形状.

图19 给出了不同雷诺数下的一个周期tref=10 s内的圆柱表面时均升阻力系数的相对误差，从图中可以看出，当雷诺数Re=100 和3 900 时，圆柱的尾流区域处于稳定涡涡脱落状态，对升阻力系数的重构误差均在25%以内，雷诺数Re=3 900 时均升阻力系数会略有增大，但变化较小，均在5%以内.随着雷诺数的增大，流动结构逐渐复杂，重构误差逐渐增大，在雷诺数Re=100 000 时，时均升阻力系数的预测误差达到55%左右，这与神经网络对大梯度变化不敏感有关，在上文已详细阐述.可以看出，随着流场结构逐渐复杂，物理信息驱动型神经网络对流场水动力特性的重构能力在逐渐降低.

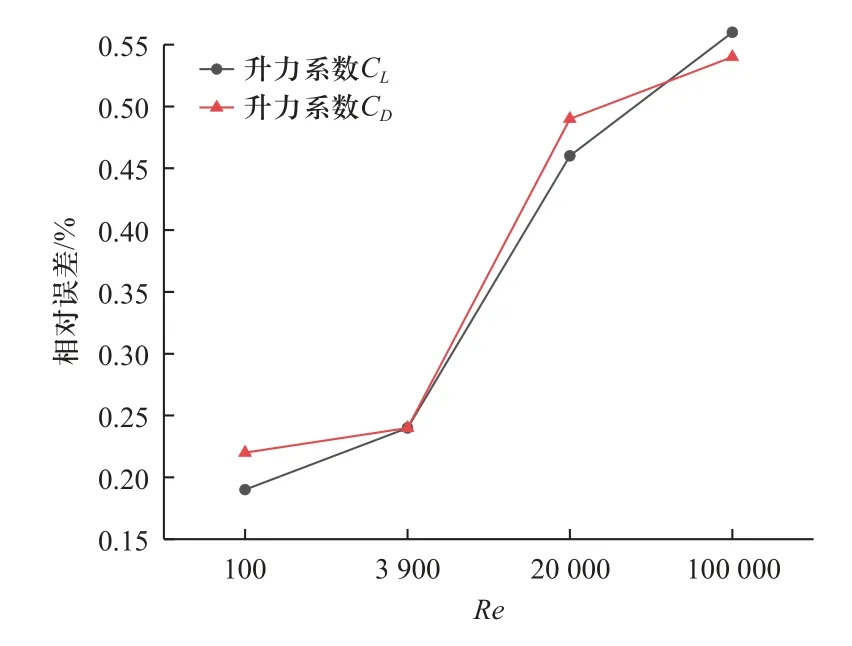
图19 不同雷诺数下升阻力系数时均相对误差Fig.19 Average relative error of lift-drag coefficient at different Reynolds numbers

4 结束语

本章首先介绍了物理信息驱动型神经网络在流体力学中的应用情况.接着发展了基于Fortran 自编程序的圆柱绕流数值求解方法，并将其作为神经网络的输入数据集.以PINN 框架为基础构建了耦合流场物理信息的神经网络模型，建立了物理信息驱动的流场结构重构方法，同时根据具体流场结构针对性提出神经网络的数据采样方式和优化策略.最后探讨了该方法对不同流态的流场重构能力，揭示了神经网络的重构误差机理，具体内容如下：

①通过输出误差的对比将神经网络确定为双权重修正模型.确定数据项平衡权重α取300 最为合适，垂向速度v误差修正权重λ取100 最为合适.

②对比分析物理信息驱动型神经网络的重构精度.结果证明，神经网络利用稀疏数据和流动控制方程即可实现对流场的精准重构.通过对比涡量云图，证实了神经网络可以精准重构流场涡结构，但在涡量大梯度变化且数值较小处预测能力欠佳.

③对比分析了物理信息驱动型神经网络对不同流态流场的重构能力.针对尾涡初始脱落（Re=100），尾涡稳定脱落（Re=3 900），尾涡亚稳定脱落（Re=20 000）以及尾涡不稳定脱落（Re=100 000）的四种流动状态，探讨了神经网络在不同雷诺数下对单相不可压缩流场的重构情况.在Re=100 时，数值模拟和神经网络模型对流场结构的结果基本一致.在Re=20 000 和Re=100 000 时，神经网络受限于流场多尺度效应，仅能较为精准的预测剪切层破裂前的大尺度涡结构.同时随着雷诺数增大，神经网络对流场升阻力系数预测能力逐渐降低.

（责任编辑：孙竹凤）