圆柱与圆锥镶嵌中侧面交线的轨迹问题①

侯宝坤

(上海市向明中学 200020)

1 问题的发现与提出

在生产生活中，我们经常遇到如图1所示的机械设备，它是一个几何结合体.其制作关键是两个几何体在对方侧面上留下的轨迹是什么. 这是一个高中阶段鲜有涉及的数学建模问题.本文将对圆柱与圆锥镶嵌问题做一些研究，揭示这类机械设备的制作原理，同时发现一些有趣的曲线.当圆锥与圆柱的底面相互垂直时称为垂直镶嵌，当圆锥与圆柱的底面相互平行时称为平行镶嵌.

2 问题的探索与解决

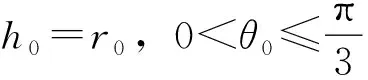
图1是一个圆锥垂直镶嵌在圆柱上，在侧面形成对称的两段交线.图2是它的立体原理图，其中A为交线的最高点，B为最低点，G为线段AB的中点；过交线上任一点C作平行于圆柱底面的截面，其圆心为O，与交线的另一交点为E，交圆柱母线AB于H；过C、E作平行于圆锥底面的截面，圆心为O1，交圆锥母线SA于F；OH、CE、O1F相交于D.设AB=2l0，SA=ρ0，SG=h0，圆锥母线与底面所成角为θ0，OH=R，O1C=r，CE=2CD=2l，∠COD=α，∠CO1D=β.

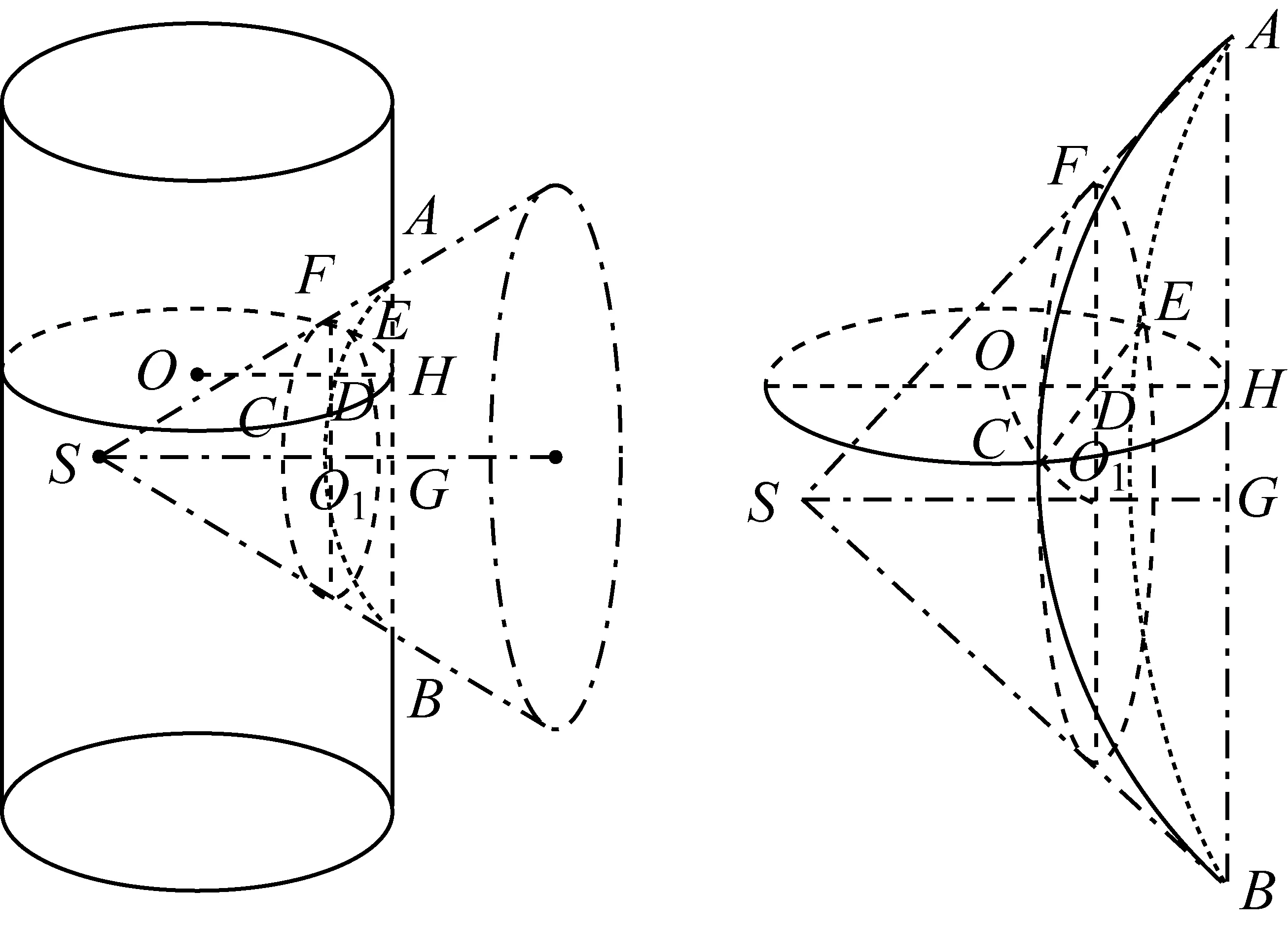
图2 机械原理图

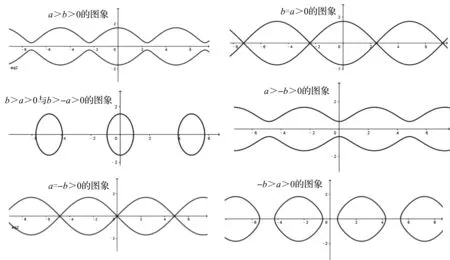
图3 y2=a+bcos cx的典型

2.1 交线在圆柱侧面上的轨迹

将圆柱侧面由母线AB向两侧展开成平面图形，再以直线AB为y轴，线段AB的中垂线为x轴，建立直角坐标系，根据对称性，我们只推证C满足x≥0的情形：

故y2=O1D2=O1C2-CD2=r2-R2sin2α

结论1交线在圆柱侧面的轨迹方程为

是一个与三角函数相关的对称曲线.

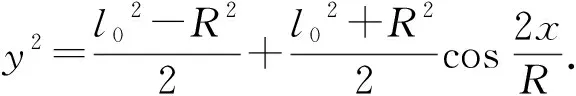
于是，我们可以构造一般曲线y2=a+bcoscx，(abc≠0)，并画出它们的图象.

2.2 交线在圆锥侧面上的轨迹

以S为原点，SA为极轴建立极坐标系.SC为极径ρ，侧面展开图的圆心角∠ASC为极角θ.

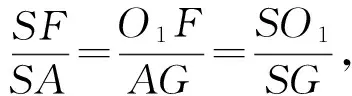
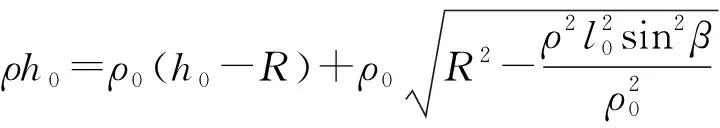
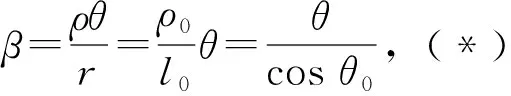
所以，极坐标方程为

结论2在圆锥侧面的极坐标方程为

特别地，当h0=R时，得到化简的极坐标方程：

于是，可以构造更一般的极坐标方程：

由于a，b变化时图象的形状大致相同，下面画出a=b=1，k在变化的一些图象(如图4)供大家欣赏：

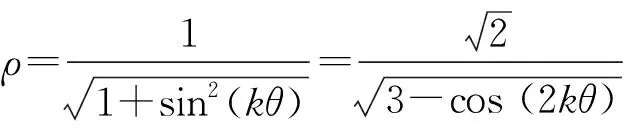
2.3 溯源寻根

一般地，曲线ρ=coskθ(**)称为玫瑰线，具有如下性质：

(1)m，n都为奇数，曲线关于极轴对称，不关于极垂线对称；周期为mπ.

(2)若m，n一奇一偶数，曲线关于极轴对称，也关于极垂线对称；周期为2mπ.

证明因为(ρ，θ)适合方程(**)，(ρ，-θ)也适合方程(**)，故图象关于极轴对称.

图象关于极垂线对称的充要条件是：对任意适合方程(**)的(ρ，θ)，存在整数k，使得(ρ，2kπ+π-θ)或(-ρ，2kπ-θ)也适合方程(**).

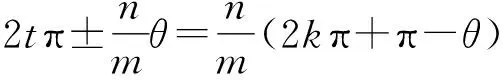
所以必须有2tm=n(2k+1)或(2t+1)m=2kn.

(1)若m，n都为奇数，显然两式都不可能成立.

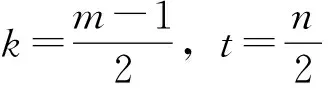
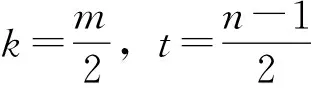
周期性证明如下：

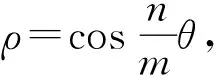
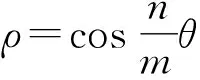
所以，曲线的周期为mπ.

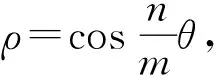
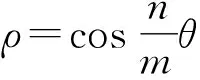
而θ=θ0+2mπ，代入显然重合.所以，曲线的周期为2mπ，不是mπ.

同理，若n为偶数，m为奇数，亦如此. 证毕.

同理可证如下：

(1)若m，n都为奇数，曲线关于极轴对称，不关于极垂线对称；周期为mπ.

(2)若m，n一奇一偶数，曲线关于极轴对称，也关于极垂线对称；周期为2mπ.

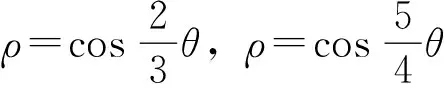
图5 半周期与全周期图

3 问题的拓展延伸

当原问题得到较圆满的解决后，通常会类比提出相似的实际问题或纯理论的数学问题，来验证原研究的思路和结论，尽量扩大问题所蕴藏的思维价值.

3.1 圆柱垂直镶嵌在圆锥上

如图6，A为交线的最高点，B为最低点，过交线的任一点G作平行于圆锥底面的平面，截圆锥为圆O1，截圆柱为矩形EFHG，EF的中点为D.设SO1=h0+d，CD=d，OE=r0，O1G=r，∠GO1D=α，∠COE=β，圆锥母线与其底面所成角为θ0.

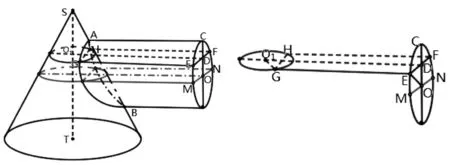
图6 圆柱镶嵌在圆锥侧面示意图

3.1.1 交线在圆柱侧面上的轨迹

将圆柱侧面由母线AC向两侧展开成平面图形，以直线AC为y轴，以过AC与ST交点的圆柱底面展开线为x轴，设G(x，y)，则有x=βr0，根据对称，只研究0≤β≤π部分.

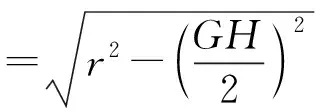
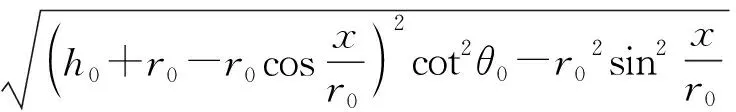
结论5在圆柱侧面轨迹方程为

即(h0+r0-r0cosβ)cotθ0≥r0sinβ(***)对β∈[0，π]恒成立.

化简，有(h0+r0)cosθ0≥r0cos (β-θ0)，

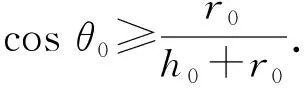
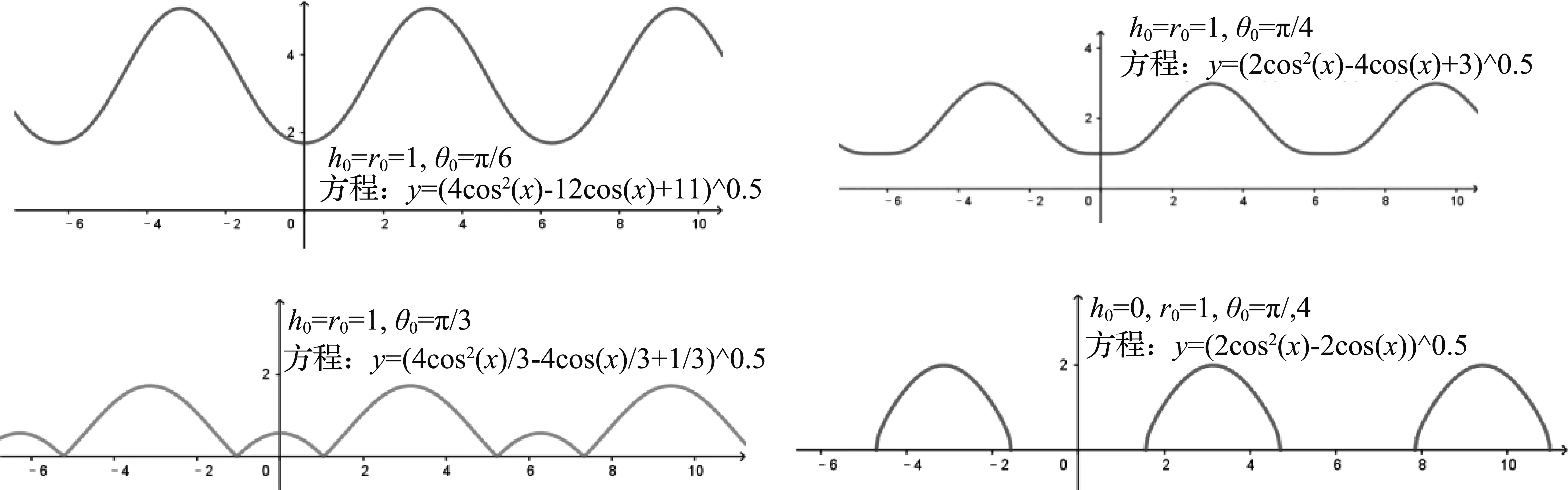
图7 在圆柱侧面上的几个轨迹图象

3.1.2 交线在圆锥侧面上的轨迹

以SA所在直线为极轴，向两侧展开圆锥，展开图的圆心角∠ASG=θ，SG=ρ.

=(2r0-ρsinθ0+h0)(ρsinθ0-h0)，

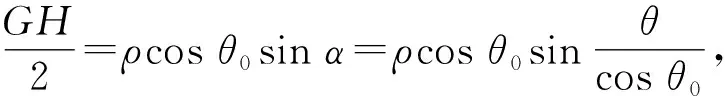
结论6交线在圆锥侧面上的极坐标方程为

(2r0-ρsinθ0+h0)(ρsinθ0-h0)

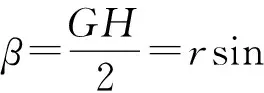
所以，极角θ范围为

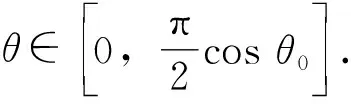
图8 在圆锥侧面上的几个轨迹图象

特别地，当h0=0时，

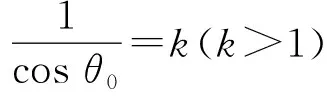
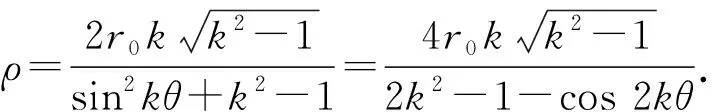
取不同的r0，k，画出图象(如图9)供大家欣赏：

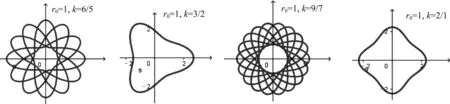
图9

如果对周期比较大的曲线画出不同区间的图象(如图10)，我们还会发现曲线都有以最短极径为半径的内切圆和以最长极径为半径的外切圆.

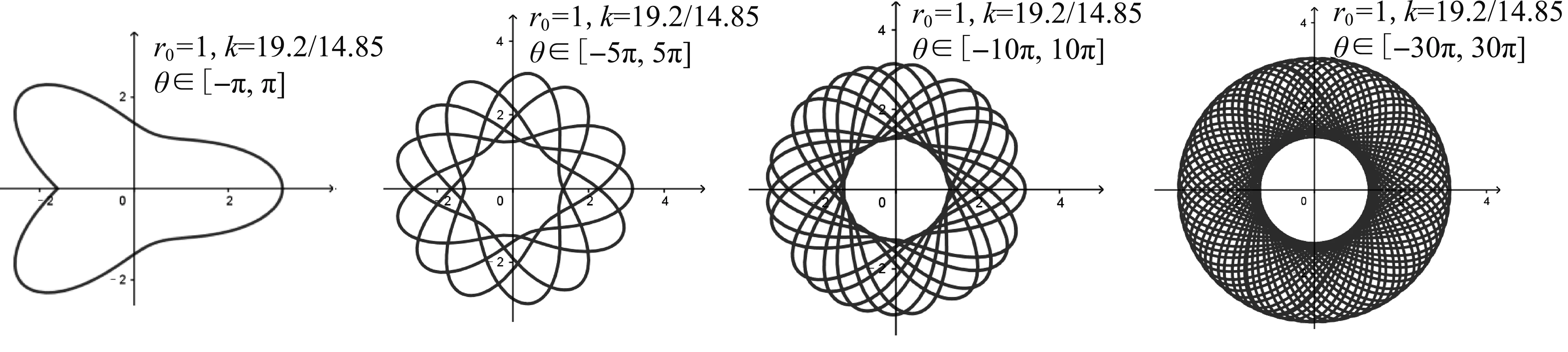
图10

3.2 圆柱与圆锥平行镶嵌

如图11，圆柱和圆锥平行镶嵌，交线的最高点为A，最低点为E，圆锥底面圆心为D，圆柱底面圆心为O，P为交线上任一点，PT垂直底面于T.设圆柱的底面半径为r，∠EOT=β，圆锥的底面半径为R，∠EDQ=α，SD=h0，SE=ρ0，AC=l0.

3.2.1 交线在圆柱侧面上的轨迹

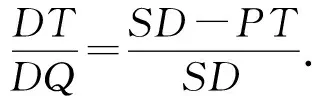
结论7圆柱与圆锥平行镶嵌时，交线在圆柱侧面的轨迹方程为

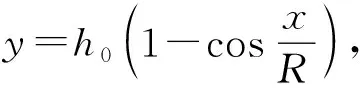
3.2.2 交线在圆锥侧面上的轨迹

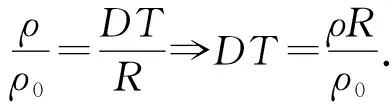
又r2=DT2+(R-r)2-2DT(R-r)cosα，再利用(*)化简得：

结论8圆柱与圆锥平行镶嵌时，交线在圆锥侧面的轨迹方程为

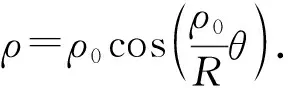
圆柱与圆锥平行镶嵌时，图象比较简单，这里不再画出.

4 探究启示

许多数学问题来源于现实生活，数学研究的初步设想往往是生活需求激发的，本文就是由生活中的发现而引起的数学探究.但数学又应当高于生活，生活给了研究的灵感，研究不应局限于生活中最原始的例子，应当做适当的类比、挖掘，作更一般的推广拓展，实现“由例到类”的思维跨越.后两种情形探索既体现了研究过程对理论的自觉追求，又凸显了理论对研究过程的引导与统率功能，从而提高了问题的思想深度，提升了研究的思维层次和理性价值.

通过上述探究过程发现，圆锥与圆柱镶嵌时侧面交线的轨迹与三角函数有紧密关联，交线在圆柱侧面上的轨迹图形相对简单，在圆锥侧面上的轨迹图形形式多样，注意灵活选用坐标形式，降低解题难度.在圆锥侧面的轨迹变化多端、赏心悦目，所有变化与圆锥母线与底面夹角的关系特别紧密，主要体现在式(*)的反复应用和曲线类型的变化上.组合体研究的关键在于发挥公共元素的桥梁作用，从而建立不同图形间元素的联系，解题时要抓牢、善用.对问题的研究要善于类比、挖掘问题的各种变化，努力寻找问题变化背后的规律，归纳出问题所蕴含的思想根源，抓住典型问题，牵一发而动全身，主动实现思维提升.

高中阶段对立体几何轨迹的研究主要集中在平面上，对侧面(曲面)上轨迹的研究极为少见.如果能对这类问题寻找一个适合的情境，提出的问题比较新颖，能有效调动学生的学习热情，提高参与探究的积极性，研究过程有利于学生立体感的培养；通过底面、侧面，以及不同几何体间的切换，有利于学生综合认识组合体的性质；利用圆柱、圆锥的侧面展开图，体现数学中化曲为直的思维方式；直角坐标系与极坐标系的不同选择，既体现了研究几何问题的不同手段，也体现了算法工具与算法思想的化简价值.本案例体现了生活处处有数学，本研究可以用作学生研究性学习和数学建模教学的素材，引领学生发现生活中的数学美，直、平、曲的自然出现、有机融合吸引了学生的目光、震撼了心灵，凸显了数学的广泛应用性和深刻的思想性.