Mode dynamics of Bose-Einstein condensates in a single-well potential
Yaojun Ying(应耀俊), Lizhen Sun(孙李真), and Haibin Li(李海彬)
Department of Applied Physics,Zhejiang University of Technology,Hangzhou 310023,China
Keywords: Bose-Einstein condensate,mode-coupling,dynamics,symmetry
1.Introduction
The realization of Bose-Einstein condensates(BECs)has triggered great research interests from both theoretical and experimental sides.[1-3]The dynamics of condensate in a confined geometry at zero temperature is described by the Gross-Pitaevskii (GP) equation.[4,5]The GP equation is a nonlinear equation that is derived in the framework of mean-field theory,[6]taking into account the effect of interaction between atoms.However, it is hard to find the rigorous results of the GP equation because of the existence of the nonlinearity term.In general,in the case of small oscillation,the elementary excitation can be described by the hydrodynamic equation or the Bogoliubov-de Gennes equation.[7,8]
The Josephson effect[9]is a clear manifestation of macroscopic quantum coherence originally found in superconducting circuits.Two weakly coupled Bose-Einstein condensates in double-well potential constitute an analogy for the study of bosonic Josephson junction.[10-12]Such a system can be described by two-mode theory.[10-27]Usually, the two modes are taken as the individual ground state mode of a single particle in an isolated trap corresponding to the right and left well, and approximately, they are the linear combination of the ground state mode and the first excited mode of the total system.In this context, the Josephson oscillation and selftrapping of condensate were predicted[11,12]and observed in experiment,[28]which indicates that the two-mode method is a good approximation and can be used to describe the dynamics of BECs.
A BEC in a single-well potential is a more typical model.The dynamics and other properties of BECs are often studied in this system.Although the frequencies spectrum of the elementary excitation of low energy can be investigated analytically and the dynamics of BECs can be simulated by numerical method, the detailed description of dynamics evolution is still lacking.In this paper, we employ the principle of the two-mode theory to study the dynamics of BECs in a singlewell potential.Our first aim is to investigate the time evolution of the amplitude of modes which are mainly occupied by a BEC and find the underlying mechanism which determines the mode dynamics of the BEC.Our second aim is to study the validity of two-mode theory in research of BEC in a singlewell potential.In the two-mode theory,the mode coupling can be caused by external potential and nonlinear interaction.We find that the coupling between modes is strongly dependent on the symmetry of the mode,which leads to a result that the two-mode model is not suitable for describing the dynamics of the BEC in a single-well potential.More modes, at least the second excited mode and the third excited mode, should be considered and in this way,we construct a four-mode model.
The paper is organized as follows.In Section 2,we consider an ideal BEC without interaction in a single-well potential.By modifying the potential with perturbation, we introduce a linear coupling between modes.The analysis and the numerical results show the dependence of coupling on symmetry.In Section 3,the dynamics of the BEC with the interaction between atoms within a single-well potential is studied.The analysis of the coupling between modes due to the nonlinearity is presented.Using the numerical method,the time evolution of the population and the amplitude of each mode are obtained.The initial conditions are found to play an important role in the dynamics of the bosonic system through the coupling between modes.Finally,a conclusion is given in Section 4.
2.Ideal BEC in nonharmonic trap
Let us first consider an ideal BEC.For the sake of simplicity,we only investigate a one-dimensional system.Because no interaction exists between atoms, the GP equation describing the dynamics of the condensate wave function has the form of the linear Schr¨odinger equation
whereV(x) is an external symmetric potential.Commonly,the trap just has one minimum, so it is called a single-well potential and can be approximated by harmonic potential,V0(x)=(1/2)mω2x2.Throughout this paper,we set ¯h=m=ω=1.According to the quantum mechanic, the solution to Eq.(1) can be obtained, i.e.,ψ(x,t) =∑i cie-iEitφi, whereφiis the eigenmode of HamiltonianHwith eigenenergyEi,Hφi=Eiφi.In this case, ifφiis normalized, it will be the eigenmode of one-dimensional harmonic oscillator.In the time evolution,there is no coupling between modes,and each mode evolves at its period.The population of each mode,|ci|2,is independent of time and just determined by the initial condition.
To investigate the coupling between modes, we first introduce a mode coupling by adding a perturbationV'(x)in the external potential to make it nonharmonic.Considering the condensate confined in the potential,V(x) =V0(x)+V'(x),we select the eigenmodes of the system in harmonic potentialV0(x) as the basis of the system and denote them byφi.The wave function of Eq.(1)with new external potential can be written as
whereai(t) is the amplitude ofi-th mode.Substituting the above formula into Eq.(1), we can obtain the coupled equation of mode amplitude as follows:
Due to the existence ofV', the coupling term appearing in the equation of each mode amplitude is in proportion to the integral of the product of two modes and external potential,∫φiV'φjdx,which is defined as coupling strengthKi j.We find thatKi jis dependent on the symmetry of the mode.Ifi-th mode andj-th mode have different symmetry,Ki jwill be zero,regardless of the form of the mode.Thus,there is no coupling between such two modes.On the contrary,if two modes have the same symmetry, in general, the integral will not be zero,then the coupling will occur between these pairs of modes.
As condensate emerges at very low temperatures, it is reasonable to assume that only a few modes with the lowest eigenenergy are excited and only the first excited mode needs to be considered.Such an idea provides the premise of the two-mode theory, which is usually used to study the dynamics of condensates in a double-well potential.In this context,due to the geometry of double-well potential,the local ground state modes of two wells are also constructed as the basis of the two-mode approach.However, this is a general idea, and its application should not be limited to the configuration of potential.More simple employment should be involved in the study of the dynamics of BECs in a single-well potential without a barrier.Because there is just one minimum in such a kind of trap, it is meaningless to build local modes.The natural choice of two modes is the ground state mode and the first excited mode.However, in the case of an ideal BEC in a single-well nonharmonic potential,as discussed above,only the pair of modes having the same symmetry can couple,there is no coupling between the ground state mode and the first excited mode.The two-mode theory is no longer valid and cannot be used to model the system in this case.We should take account of more modes in the studying of dynamics of BECs in a single-well potential.Under the condition of low temperature,together with the rules of the coupling described above,the second excited mode and the third excited mode should be included in our new approach.According to Eq.(4), we can obtain four coupled dynamics equations of the mode amplitude as follows:
It is clear that the ground state mode couples with the second excited mode while the first excited mode couples with the third excited mode, which decouples the equations into two pairs of coupled equations.That is to say,each pair of coupled equations satisfies the two-mode theory and the total system can be decomposed into two independent subsystems.
Next, to testify to our analysis, we perform a numerical simulation of the GP function without nonlinearity interaction.We setV'=0.05x4.Before the simulation, we first calculate the coupling strength explicitly using the eigenmodes of the ideal boson system in harmonic trapV0, i.e., the eigenmodes of a single boson in such a trap.The coupling between modes with different symmetries is zero(K12=K14=K23=K34=0)while the coupling between modes with the same symmetry is nonzero(K13=-0.0106,K24=-0.0305).
In the simulation, the amplitude, real part of the mode amplitude,and population of each mode can be calculated byai(t)=∫φ∗i ψ(x,t)dx,bi(t)=Re(ai(t)), andpi(t)=|ai(t)|2,respectively.The initial condition of the wave function is prepared as the superposition of the ground state mode and the first excited mode,
wherea0(0) anda1(0) are the initial complex amplitudes of the two modes,satisfying norm condition

Fig.1.(a)The mode population of four modes versus time.(b)Fourier spectrum of population of four modes.The initial condition is a0(0)=1,a1(0)=0.

Fig.2.(a)The mode population of four modes versus time.(b)Fourier spectrum of population of four modes.The initial condition is a0(0)=a1(0)=2/2.
When all atoms of the BEC initially occupy the ground state mode,i.e.,a0(0)=1,the time evolution of the population of the four modes is calculated as plotted in Fig.1(a).We find that only the amplitudea2(t)becomes nonzero and presents an oscillation as well as the ground state mode.The oscillation of two amplitudes is almost sinusoidal.The frequency analysis of the mode population, as plotted in Fig.1(b), shows the same period of these two oscillations,which indicates the coupling between them.If we set the initial condition as the first excited mode,a1(0)=1, a similar scenario will occur such that only the third excited mode is stimulated which verifies the coupling between such two modes.We also set the initial condition assuch that the ground state mode and the first excited mode are occupied equally.In Fig.2(a),we can observe that the second excited mode and the third excited mode are all stimulated and all four modes are oscillating with time.However,the frequency analysis shows that the ground state mode and the second excited mode have the same frequency,while the first excited mode and the third excited mode have the same frequency.The difference between these two sets of frequencies shows the independence of the two sets of modes.
3.BEC with interactions in a trap
3.1.Theory
An ideal BEC is hard to achieve and, in reality, the interaction does exist between atoms.Next,we consider a onedimensional bosonic condensate ofNparticles with interaction.The GP equation describing the dynamics of the condensate wave function takes the form
andu0=gN, wheregis the interaction strength.Ifgis nonzero,the GP equation is a nonlinear Schr¨odinger equation to which there is generally no exact solution.Some approximations are taken to capture the basic physics of BEC in a trap,including the two-mode theory.V(x,t) is the external potential.In this study,we setV(x,t)as harmonic potential,but our conclusion is valid for general external potential.Then we can still use the eigenstates of ideal BEC in a harmonic trap as target modes.The nonlinear term can be treated as perturbation and will lead to the coupling between modes.As discussed above, mode coupling is totally dependent on the symmetry of mode when it is caused by a nonharmonic part of the trap,and more modes should be included in the description of the dynamics of BECs.For the same reason, when considering BEC in a harmonic trap with interaction, it is reasonable to include more modes.We still assume that the four modes,corresponding to the four lowest eigenenergies, should be taken into account.Then the condensate wave function can be written by a superposition of four modes as
Substituting the above formula into Eq.(7),we can reach the four-coupled-mode equation
The coupling between modes has a nonlinear form that is determined by the integral of the product of four eigenmodes, which means that it is difficult to get the exact solution of the above equation.Unlike the ideal BEC in a nonharmonic trap where one coupling term only makes two modes coupled, here there are three kinds of coupling between modes.The first one is two-mode coupling which is caused by coupling integral containing two kinds of modes
like∫φ∗i φ∗i φiφj(i/=j)dx.Between the two modes,there are 7 two-mode coupling terms.The second one is three-mode coupling with integral likeand among three modes, there are 12 coupling terms.The third one is four-mode coupling whose strength is determined by the integralThe number of four-mode coupling in one equation is 6.
In addition, unlike the two-mode coupling between modes of an ideal BEC in a nonharmonic trap,which is determined completely by the symmetry of modes,the dependence of two-mode coupling caused by nonlinear interaction on the symmetries is more complex.Two modes that have different symmetries could be coupled by such nonlinear coupling.However,the coupling between modes with the same symmetry still has large difference from the coupling between modes with different symmetries.In Eq.(9), there are seven twomode coupling terms between the two modes.If they have the same symmetry, then all the coupling integration is nonzero.If they have different symmetries,only three-coupling integral are nonzero.For example, the coupling integral between the ground state mode and the second excited mode isK0002=K0200 =K0020= 0.1413,K0022=K0202=K0220= 0.1510,K0222=-0.0175.The coupling integral between the ground state mode and the other modes isK0011=K0101=K0110=0.1997,K0033=K0303=K0330=0.1253.
Except for the coupling strength, according to Eq.(9),the coupling term is also proportional tou0and dependent on the initial conditions as it is proportional to the third power of mode amplitude.In the following, we first investigate the mode dynamics under different initial conditions by performing numerical simulations of the GP equations.To this end,the initial condition of the wave function is still set as the superposition of the ground state mode and the first excited mode,ψ(x,0)=a0(0)φ0(x)+a1(0)φ1(x).
3.2.Zero excitation
Assume that the initial condition is prepared as the ground state mode of the ideal BEC, i.e.,a0(0) = 1,a1(0) = 0,which means that there is no excitation at the beginning.The time evolution of the population of four modes is plotted in Fig.3(a).We find that only the second excited mode is ignited and makes an oscillation,similar to the case of no interaction.Asa2(0)=0, it is clear from Eq.(9) that this excitation is stimulated by the coupling with the strengthK0002=0.1413,K0022=0.1510,K0222=-0.0175.In the meantime, the first excited mode and the third excited mode are not ignited and always remain zero.This is consistent with the analysis of Eq.(9)that the coupling also depends on the initial condition.The amplitudes of population oscillation of the ground state mode and the second excited mode are small,and the average value of the population of the second excited mode is much smaller than that of the ground state mode.This feature is also exhibited by the time evolution of the real part of mode amplitude plotted in Fig.3(c).That is to say, only a small fraction of condensate atoms exchange between two modes.It is attributed to the small coupling strength and large energy gap between the two modes.
The frequency analysis in Fig.3(b) shows that the population of two modes have the same spectral structure,which indicates that they oscillate at the same frequency.In the spectrum,the frequencyω=1.82 has the largest amplitude which dominates the dynamics as seen in Fig.3(a).The frequency analysis of mode amplitude plotted in Fig.3(d)shows that the oscillations of amplitudesa0(t) anda2(t) have two main frequencies,denoted byω1iandω2i(i=0,2),respectively.It can be seen that the frequencies of the ground state mode are identical to that of the second excited mode,i.e.,ω10=ω12=1.75,ω20=ω22=3.60,which lead to the equality of the frequencies of populations|a0(t)|2and|a2(t)|2.

Fig.3.The mode population of four modes(a)and the real part of mode amplitude(c)versus time.The Fourier spectrum of the mode population(b)and the real part of mode amplitude(d).The initial condition is a0(0)=1,a1(0)=0,u0=4.
In Eq.(9),we can see that the coupling is caused by nonlinear interaction and call it nonlinear coupling, which leads to the coupling between any pairs of modes no matter what symmetry they have.However, when the initial condition isa0(0)=1,the picture of mode dynamics is similar to the case of linear mode coupling, as shown in Section 2, the modes having the same symmetry as the ground state mode can be stimulated.In addition,considering the intensity of excitation,the higher mode can be ignored.In this way the system can be described by a pair of the coupled equations in Eq.(9),the first and the third one describe the dynamics of the ground state mode and the second excited mode, respectively.The second equation and the fourth equation in Eq.(9)for the odd symmetric mode can be ignored because they are not excited.That is to say,the system becomes a two-level system and we can still use the two-mode method to describe its dynamics.
3.3.Weak excitation
To observe the dynamics of the system when the first excited mode is weakly stimulated, we set the initial condition|a0(0)|≫|a1(0)|>0.In Fig.4(a), the dynamics of the population of four modes is illustrated.We can clearly observe that in the time evolution,except for the second excited mode,the third excited mode is stimulated and occupied by atoms.The population of four modes oscillates with time.However,the amplitude of population oscillation differs distinctly.The ground state mode has the largest average oscillation amplitude while the second excited mode presents a smaller one because of energy difference and initial condition.The third excited mode is also stimulated because of the nonzero initial value of the population of the first excited mode.The amplitude of the population of the third excited mode is smaller than that of the first excited mode.

Fig.4.The mode population of four modes(a)and the real part of mode amplitude(c)versus time.The Fourier spectrum of the mode population(b)and the real part of mode amplitude(d).The initial condition is a0(0)= ,a1(0)=,u0=4.
In the frequency analysis of the oscillation of the mode population in Fig.4(b), we can find that each mode has four sets of frequencies, near 0, 2, 4, 6, respectively.In each set,there is a main central frequency with high amplitude, while to the left and the right of this main frequency there are two secondary frequencies of very low amplitudes.Remarkably,the main frequencies of the population of these four modes are all the same, i.e.,ω0i=0.1678,ω1i=1.831,ω2i=3.661,ω3i=5.49 (i=0,1,2,3), whereiis the sign of mode, while their corresponding amplitudes are different.It is also noted that these main frequencies of four modes are also identical to the main frequencies of the corresponding mode populations in the case of zero excitation, which is the intrinsic property of coupled equations.However, there are a few frequencies present in the weak excitation but absent in the zero excitation.They occur near the main frequency as secondary frequencies.It is attributed to the excitation of the first excited mode and its coupling with other modes.In addition, the distributions of the amplitude of the four modes populations are not totally the same.However, according to the order of amplitude, the ground state mode and the second excited mode have the same frequency distribution, while the first excited mode and the third excited mode have the same frequency distribution.For the former pair of modes,a high frequencyω=1.831 has the largest amplitude, but for the latter pair of modes, a low frequencyω=0.1678 has the largest amplitude.
As the frequency of the mode population is completely determined by the frequency of mode amplitude,the frequency spectra of mode amplitude are also analyzed and plotted in Fig.4(d).Compared to the frequency spectra of the mode population,a different scenario shows in the frequency spectra of mode amplitude.The amplitude of the ground state mode and the amplitude of the second excited mode have the same frequency,while the amplitude of the first excited mode and the amplitude of the third excited mode have the same frequency.Yet,each frequency of the mode amplitude of the ground state mode and the second excited mode is not equal to any frequency of the mode amplitude of the first excited mode and the third excited mode.
Based on the above frequency analysis of mode amplitude, we can find that the ground state mode is mainly coupled with the second excited mode because their amplitudes oscillate at the same frequency.For the same reason,the first excited mode is mainly coupled with the third excited mode.These results are consistent with the previous finding that the total coupling strength between two modes is dependent on the symmetry of the mode.In this way,the whole system can be approximately divided into two subsystems, each of which is composed of two modes with the same symmetry and can be modeled as a two-level system.The exchange of atoms mainly takes place inside these two subsystems.
Although the frequencies of mode amplitude with odd symmetry are not identical to that of modes with even symmetry, after the operation of modulus, the frequencies of the population of four modes are the same, as discussed above,which makes all four modes coupled together in this level.As shown in Figs.4(b)and 4(d), we notice that the coupling between modes with different symmetries is mainly exhibited by the low-frequency oscillation which modulates the amplitude of high frequency oscillation.However, this modulation is small because this low frequency has a small amplitude in frequency spectrum.Then the above decomposition of the system still holds,but two subsystems are coupled weakly through low-frequency oscillation.Considering the smallness of the mode population of the first excited mode and the third excited mode, the dynamics of the system is mainly determined by the subsystem composed of the ground state mode and the second excited mode.The most transformation of atoms appears in this subsystem.
3.4.Intermediate excitation
Initially,ifa0(0)is set to be larger than that in the case of weak excitation,the system will be more strongly excited.In Fig.5(a),we can see that the system shows different dynamics behavior.The population of four modes still exhibits oscillation, while the amplitude of the first excited mode and the third excited mode is not small, but as large as the amplitude of the second excited mode.It is clear that the initial condition leads to the large amplitude of the first excited mode.The large amplitude of the third excited mode should be attributed to the coupling with the first excited mode and other modes.
In the frequency analysis of population oscillation, we can observe four sets of frequencies,each set consisting of one central frequency and two main secondary frequencies.Moreover,there are more frequencies with very small amplitude appearing in spectra.Each of the four modes has the same main central frequency.These frequencies in the spectrum are identical to the frequencies presented in the population oscillation of the system under the zero excitation and weak excitation initial condition.However, for the amplitude of frequency of the four modes,there is a common character that the low frequency has the largest amplitude.This is different from the case of the weak condition.The frequency analysis of mode amplitude is shown in Fig.5(d).It is still shown that the amplitudes of the ground state mode and the second excited mode have the same frequency which is not identical to the ones owned simultaneously by the first excited mode and the third excited mode.
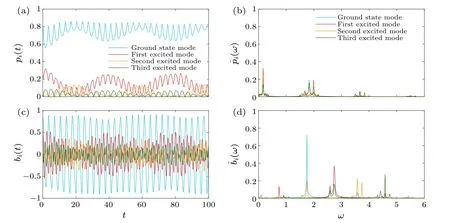
Fig.5.The mode population of four modes(a)and the real part of mode amplitude(c)versus time.The Fourier spectrum of the mode population(b)and the real part of mode amplitude(d).The initial condition is a0(0)=25/5,a1(0)=5/5,u0=4.
In the time scale of a period of the population with high frequency, we notice that the population of the ground state mode and the second excited mode has an anti-phase oscillation, while the first excited mode and the third excited mode have an in-phase oscillation.However, in the time scale of a period of the population with low frequency, the populations of the ground state mode and the second excited mode show an in-phase oscillation so that the numbers of particles occupying these two modes increase and decrease simultaneously,and this is the same character of population oscillation of the first excited mode and the third excited mode.
Combining these results,we can find that under the intermediate excitation, the mode dynamics can still be described by two coupled two-mode models.The ground state mode and the second excited mode form a subsystem because of the same frequency coupling.Likewise, the first excited mode and the third excited mode form another subsystem.However, unlike the case of weak excitation, these two subsystems are strongly coupled and constitute a composite system.The dynamics of the system are mainly characterized by the oscillation caused by the coupling between two subsystems.The transfer of atoms occurs mainly between the ground state mode and the first excited mode by such low-frequency oscillation.
3.5.Strong excitation
When the initial amplitude of the first excited mode is close to that of the ground state mode,the excitation is strong.As seen in Fig.6(a),where,the oscillation of the population of four modes is no longer periodic,but irregular.In the first stage of evolution, the population of the first excited mode is even larger than that of the ground state mode.However,in the subsequent evolution,the population of the ground state mode always has the largest value.The excitation of the other two modes is still small.The frequency analysis of population oscillation in Fig.6(b)also exhibits a more complex picture.Although there still exist a few frequencies near 0,2,4,and 6,respectively,in spectrum,but around each of them many secondary frequencies appear and even form a frequency band respectively,which surely leads to the regularity of population dynamics.The low frequency has the largest amplitude which determines the dynamics.On the other hand,the real part of mode amplitude[see Fig.6(c)]of four modes seems to have irregular oscillation, but their frequencies [see Fig.6(d)]also show some frequency bands at high frequency which determines the irregularity of population oscillation.
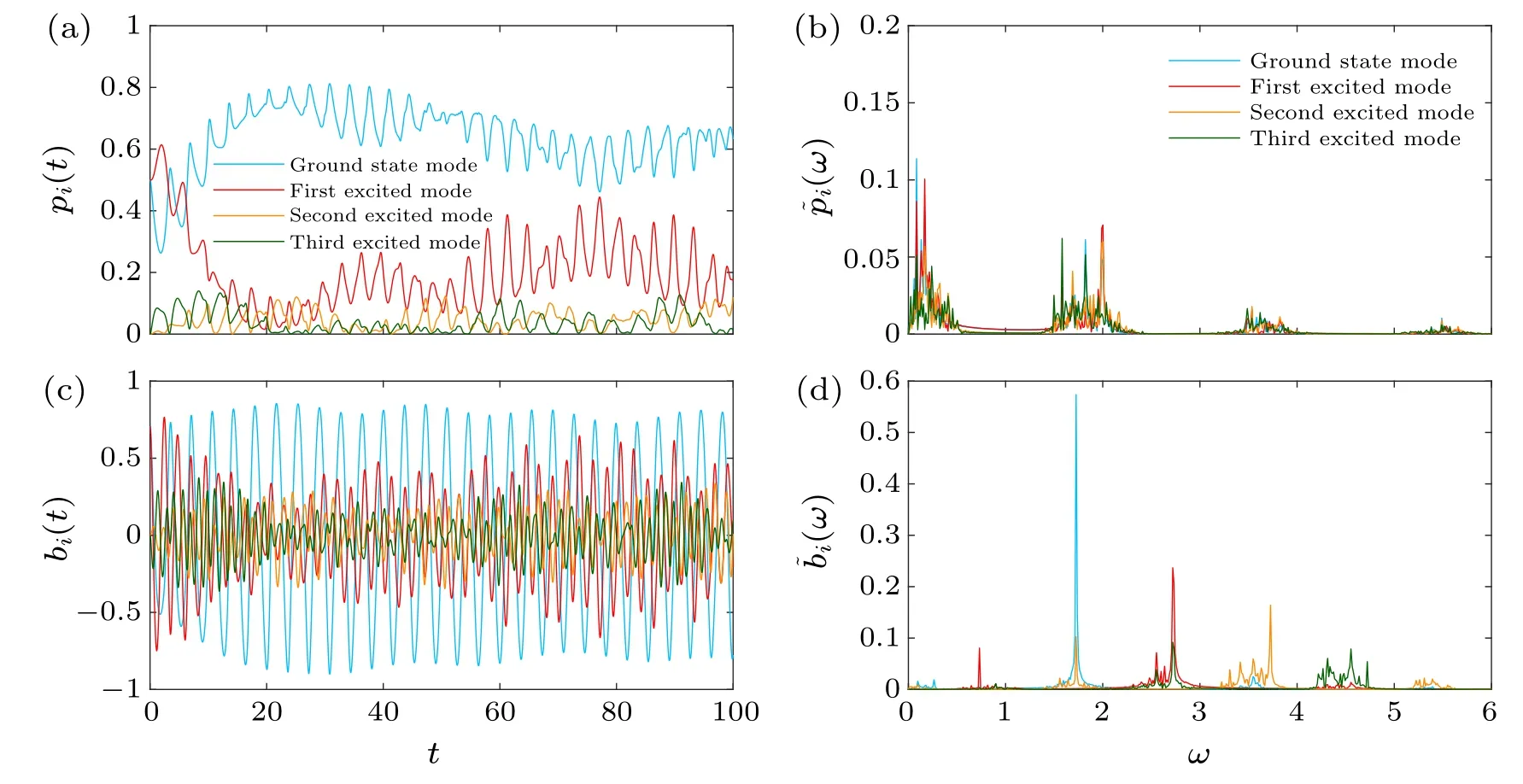
Fig.6.The mode population of four modes(a)and the real part of mode amplitude(c)versus time.The Fourier spectrum of the modepopulation(b)and the real part of mode amplitude(d).The initial condition is a0(0)=2/2,a1(0)=2/2,u0=4.
3.6.Effort of nonlinear interaction strength on dynamics
As shown in Eq.(9),the coupling between modes is also dependent on the interaction strengthu0.This effort is also studied numerically.However,we find that the results are similar under different initial conditions thatu0mainly influences the amplitude of population oscillation of excited modes in the time evolution.To illustrate this conclusion, we consider the example of zero excitation, i.e.,a0(0)=1, as seen in Fig.7.Whenu0is zero,no excitation appears and the system will stay in the ground state mode.Whenu0becomes nonzero,the second excited mode is stimulated.Ifu0is small,we notice that the amplitude of the population oscillation of the second excited mode is small as well as the amplitude of the population oscillation of the ground state mode.However, whenu0increases,the amplitude of the population oscillation of the two modes also increases.Notably, such an increase is not linear and can be divided into two stages.The first stage is characterized by a quick increase,while the second stage presents a slow increase in the amplitude.
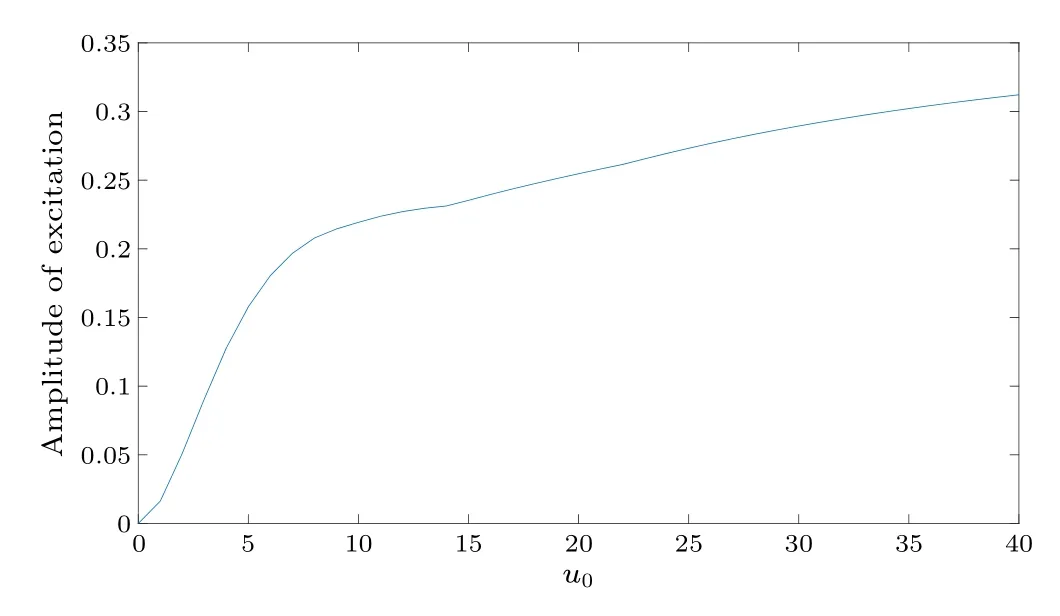
Fig.7.Relationship between u0 and excitation amplitude.
4.Conclusions
In summary, we have investigated the dynamics of BEC trapped in a single-well potential by using the mode-coupling theory, and found that the coupling between two modes depends on the symmetry of modes, and the degree of such dependence is determined by the cause of coupling.When considering the ideal BEC without interaction and introducing a nonharmonic potential perturbation which cause the mode coupling, we find that the coupling is totally dependent on the symmetry of the mode and only the modes that have the same symmetry can be coupled.We can decompose the system into two independent subsystems and each subsystem can be described by a two-mode theory approximately.However,the system cannot be approximated by just a standard twomode model which takes into account the ground state mode and the first excited mode.Noticeably, at least four modes should be included.For this reason,we use the four-mode approximation when considering that the interaction is presented between atoms and leads to the nonlinear coupling between modes.In this case,there are three kinds of coupling,including two-mode coupling, three-mode coupling and four-mode coupling, appearing in the coupled equation of mode amplitude.The symmetry of modes coupled will determine the coupling strength that the coupling between modes with same symmetry is larger than the coupling between mode with different symmetries, which means that the two-mode theory is also invalid in this case.The two-mode coupling is shown to dominate the dynamics of condensates which shows a wealth of phenomena, not only dependent on coupling strength but also dependent on the initial condition.Different scenarios of dynamics will display as the strength of initial excitation increases.In a limited case where the initial state mode of the system is the ground state mode, only the modes with same symmetry can be stimulated so that the system can still be described by a two-mode model approximately.When the initial state mode is the superposition of the ground state mode and the first excited mode,the four-mode model is a good approximation.In the case of weak excitation, the two-mode coupling between the modes with the same symmetry is dominant, determining the exchange of the population of modes.The system can be composed of two subsystems and they are coupled weakly.In the intermediate excitation regime,the coupling between the modes with different symmetries causes the large population exchange between two subsystems at low frequency.If the excitation is strong, the population of the modes exhibits irregular oscillation at many frequencies,which should be the evidence of all coupling among four modes and possible coupling between modes not including in our approximation.Lastly,the effect of interaction strength on the mode dynamics is also investigated.
- Chinese Physics B的其它文章
- Single-qubit quantum classifier based on gradient-free optimization algorithm
- A quantum algorithm for Toeplitz matrix-vector multiplication
- Non-Gaussian approach: Withstanding loss and noise of multi-scattering underwater channel for continuous-variable quantum teleportation
- Trajectory equation of a lump before and after collision with other waves for generalized Hirota-Satsuma-Ito equation
- Detection of healthy and pathological heartbeat dynamics in ECG signals using multivariate recurrence networks with multiple scale factors
- Rucklidge-based memristive chaotic system:Dynamic analysis and image encryption

