对称几何非线性三角形平面单元研究

王动，邓继华

（1.淮北市交通投资控股集团有限公司，安徽 淮北 235000；2．长沙理工大学 土木工程学院，湖南 长沙 410114）

随着高强度、轻质材料的广泛应用，工程结构不断向大跨、柔性的方向发展，结构的非线性效应也愈加明显，对结构进行整体或局部的动力、静力分析时必须考虑非线性效应的影响，才能满足安全、经济的设计要求。在这一过程中，建立各种精确、高效的单元模型，并考虑其所面对的非线性效应是关键［1-2］。目前，采用诸如ANSYS 等大型商业数值软件对结构进行非线性分析是主流的研究方法。但事实上，完全拉格朗日法（total lagrange，TL）、修正的拉格朗日法（updated lagrange， UL）以及共旋坐标法（corotational， CR 法）才是各种非线性单元分析的主要算法。相对于TL 法和UL 法而言，CR 法出现的时间较晚，且相关研究较少。因此，TL 与UL 这两种算法被ANSYS 等商业数值软件广泛采用，而到目前为止，CR法尚未被商业数值软件采用。

FELIPPA 等［3］认为CR 法仅适用于大转动、小应变的运动条件，苛刻的应用条件使其不能满足大型商业工程仿真数值软件的算法适用范围必须很宽的要求，这也是其被众多商业工程仿真数值软件弃用的主要原因。但RANKIN 等［4-6］认为在物体发生大转动、小应变的运动条件下，CR 法相对于TL 法和UL 法具有两个非常明显的优势：一是在进行非线性单元研究时，CR 法能非常方便地引入各种先进线性单元，而无须考虑推导这些先进线性单元时所采用的各种假设条件；二是在非线性列式中，几何非线性与材料非线性是解耦的，即材料非线性在共旋坐标系下进行计算，而几何非线性则通过变量在共旋坐标系与结构坐标系之间的转换矩阵被自动计入。由于工程结构中的非线性问题绝大部分都属于大转动、小应变的范围［7］，因此，基于CR 法研究各种非线性单元，对促进结构非线性效应研究具有十分重要的意义。杨浩文等［8］采用共旋坐标法建立了考虑几何非线性的Timoshenko 梁单元，并基于该单元建立了用于非线性动力分析的能量守恒逐步积分算法。冯晓东等［9］基于共旋坐标法，推导了大位移空间杆单元的切线刚度矩阵，并将其结论运用在一个对四杆张拉整体结构单元体的几何非线性弹塑性特性进行分析的研究上，该研究结果表明，相比于传统的TL 法和UL法，CL法具有更高的计算效率。邓继华等［10］将共旋坐标法和稳定函数结合起来，利用共旋坐标法考虑大位移，利用稳定函数考虑P-δ效应，多个经典算例分析均表明该非线性平面梁单元具有较高的计算精度和效率。张亮等［11］则采用共旋坐标法，推导了一个适用于充气薄膜结构褶皱分析的空间三节点的三角形膜单元。目前，也有一些学者基于共旋法对平面单元方面进行了研究。蔡松柏等［12］基于共旋法与场一致性原则，分别建立了四节点四边形和八节点四边形几何非线性平面单元。邓继华等［13-14］还将仅限于几何非线性的研究拓展到几何与材料双非线性领域。相对于四边形平面单元而言，基于共旋法分析几何非线性三角形平面单元的研究很少，笔者仅查阅到文献［15］，该文献基于共旋法与场一致性原则，对几何非线性三角形平面单元进行了研究。不过需要指出的是，邓继华等［15］与蔡松柏等［12-14］学者一样，其推导出的单元切线刚度矩阵均是非对称的矩阵，这将给非线性方程组的求解带来一定的困难。众所周知，平面三角形单元作为常应变单元，当网格化较为稀疏时，其计算精度较低；但随着单元网格数量的增加，其计算精度会迅速提高。且三角形平面单元可适用于复杂和不规则边界形状的分析［16］。因此，基于CR 法，建立具有对称切线刚度矩阵的几何非线性三角形平面单元是十分必要的。

综上所述，本研究在这些研究的基础上，针对三角形平面单元，借鉴YAW 等［17］的研究方法，采用具有对称切线刚度矩阵的几何非线性梁单元，合理选择三角形平面单元共旋坐标系的原点及坐标轴方向，基于与虚功原理相结合的几何一致性原则［18］，建立三角形平面单元在大转动、小应变条件下，具有对称特征的几何非线性单元切线刚度矩阵和相应的节点抗力算法；对于该算法中待求解的非线性方程组，采用一种能将位移增量法与荷载增量法形成统一迭代格式的新方法［19］，开发了相应的计算程序，并将该计算程序应用于大变形悬臂梁计算的两个经典算例，将该算法对这两个算例的计算结果与ANSYS 商业数值软件的计算结果进行了对比，验证了本研究建立的有限元列式和算法的正确性，且算例2的计算比较结果也表明该算法的计算精度略高于ANSYS商业数值软件的计算精度。

1 共旋法有限元列式

1.1 基本图式

变形前、后的三角形平面单元如图1所示。

图1 变形前后平面单元Fig. 1 Plane element before and after deformation

在图1 中，XOY为固定不变的结构坐标系，xoy为随单元平移和转动的共旋坐标系，取三角形3 个顶点M1，M2，M3坐标分量的平均值作为点C在结构坐标系XY下的坐标分量值。在初始时刻，x轴方向平行于X轴；在任意计算时刻，x轴的方向由刚性转角θ确定，y轴的方向则由x轴逆时针旋转90°得到。

1.2 平面单元的切线刚度和抗力矩阵

对图1所示三角形平面单元，设

式中：

为初始时刻的节点单元；

Ri为计算时刻单元在结构坐标系下的节点坐标；

ui为单元在结构坐标系下的节点位移；

为初始时刻共旋坐标系xy的原点C在结构坐标系下的坐标；

rC计算时刻共旋坐标系xy的原点C在结构坐标系下的坐标。故有

在式（2）中，uc=()UC，VC，是在计算时刻，共旋坐标系原点C在结构坐标系下的位移，故有

同时，Ri=(Xi，Yi)与之间有关系：

设=(xi，yi)，i= 1，2，3 为初始时刻单元节点在共旋坐标系下的坐标，显然有关系：

假定计算时刻单元发生节点位移ui后，共旋坐标系x轴与结构坐标系X轴的夹角θ已求出，则计算时刻单元在共旋坐标系下的节点位移= 1，2，3的计算式为

对于计算时刻x轴与X轴夹角θ的确定，可参照文献［20］中的方法。夹角θ的选取的原则是：选取能使得值最小的θ，故可将其带入式（11），这时式（11）变为θ的函数，对其进行关于θ的求导，并令该导数为0。可得

显然，由式（12）可得到两个解，分别为θ和θ+π，将这两个解代入式（11），选取使较小的那个作为最终解。

为描述方便，令

设共旋坐标系与结构坐标系下与Pl和Pg分别对应的节点力为fl和fg，设三角形平面单元在共旋坐标系下的刚度矩阵为kl，根据前面所述共旋坐标法的性质，有

由共旋坐标系与结构坐标系下虚功相等的原则［18］，有

其中，位移微分的下标v表示该变量为虚拟量。

先对式（12）进行微分，得到δθ与δPg之间的关系，再对式（11）进行微分，可得到δPl与δPg的关系，其表达式为

联立式（14）～（15），可得到fl和fg之间的关系，其表达式为

对式（16）进行微分，并联立公式（13），有

设三角形平面单元在结构坐标系下的几何非线性切线刚度矩阵为kg，即：

联立式（17）、（18），则有

且

显然，要得到kh的具体表达式，关键是求出δBT。因此，对式（11）进行变分，可得

式中：xdi=+xi；

ydi=+yi。

为求出式（21）中的δθ，对式（12）进行微分，则有关系：

联立式（21）～（22）及式（15），可得到B的表达式：

式中：P=I-AG，且有

其中，

至此，联立式（20）、（23），并考虑ATGT=I，可得到kh的具体表达式：

其中，有

将式（24）代入式（19），可得到三角形平面单元在结构坐标系下的几何非线性切线刚度矩阵为kg，其表达式为

考虑到式（25）中等号右边各项矩阵具有的特殊形式，不难证明kg是对称的。

2 非线性计算流程及方程组求解

先输入结构的初始几何、材料、荷载及边界约束等参数，再结合单元网格划分得到每个单元初始时刻在共旋坐标系下的节点坐标、原点坐标、单元刚度矩阵及总荷载矩阵，保留这些数据。在每一级荷载增量步中，迭代的具体步骤是：

步骤1：由上一级荷载增量步末的总节点位移确定当前单元的节点位移ui=()Ui，Vi，i= 1，2，3；

步骤2：由式（8）得到当前单元共旋坐标系原点C在结构坐标系下的位移(UC，VC)；

步骤3：由式（12）并结合所得θ值需使较小的原则确定单元的刚体转角值θ；

步骤4：由式（11）得到当前单元在共旋坐标系下的节点位移

步骤5：由式（13）得到当前单元在共旋坐标系下的节点力fl；

步骤6：对式（11）微分，基于δPl与δPg的关系，得到矩阵B，进而由式（16）得到当前单元在结构坐标系下的节点力fg；

步骤7：联立式（23）～（24）与（25）得到当前单元在结构坐标系下的切线刚度矩阵kg；

步骤8：对所有单元进行步骤1～7的操作，将每个单元在结构坐标系下的切线刚度矩阵kg进行叠加，得到结构总刚矩阵与总抗力矩阵；

步骤9：结构非线性平衡方程组右端的不平衡力矩阵则由总荷载矩阵减去总抗力矩阵形成；

步骤10：引入边界条件后，进行非线性平衡方程组的求解，得到当前迭代步的增量节点位移，将其与之前的总节点位移叠加，形成新的总节点位移；

步骤11：进行收敛判断，如收敛，转至下一个荷载增量步；如不收敛，进入下一个迭代步。

最常用的非线性方程组求解方法是荷载增量法和位移增量法，这两种方法均存在一些各自的优缺点。为综合利用这两种方法的优点而又能避免各自的缺点，本研究采用已有的非线性方程组求解方法［19］，该方法将荷载因子λ视为第n+ 1 个变量，从而将非线性方程组的荷载-位移求解空间由Rn扩展到Rn+1，推导出一种能集荷载增量法和位移增量法于一体的统一迭代格式，该方法在实际研究中得到了较广泛的应用［12，21］。

3 算例分析

3.1 算例1

底端固结上端自由的柔性立柱，该柔性立柱高为9 m，宽为3 m，厚为1 m，具体如图2 所示。在该柔性立柱中，自由端截面中心承受的水平力P的数值为2.777 8×109kN，所使用材料的弹性模量E为1.0×1010kN/ m2，泊松比μ为0。文献［15］基于其推导的具有非对称切线刚度矩阵的三角形平面单元对该算例进行了计算，并用ANSYS 商业数值软件进行了验证。为验证本研究推导公式和算法的合理性与有效性，将本研究的计算结果及与文献［15］的计算结果进行对比（这两种计算都是基于将柔性立柱在X轴向与Y轴方向，并按0.25 m 的间距对其进行单元网格划分的，单元网格划分均产生了481 个节点和864个单元），结果见表1。

表1 柔性立柱自由端的水平位移Table 1 Horizontal displacement at free end m

图2 承受水平集中荷载的柔性立柱（单位：m）Fig. 2 Flexible column under horizontal concentrated load（unit： m）

由表1 可知，本研究得到的解与文献［15］的解吻合良好。这是因为在求解结构坐标系下的单元节点抗力时，本研究与文献［15］都是基于先在共旋坐标系，再进行转换得到的。具体都是先用单元线性刚度矩阵乘以去除刚体后的纯变形，得到共旋坐标系下的单元节点抗力，再将其转换到结构坐标系下进行计算，计算得到的矩阵与对应阶段的荷载矩阵之差即为不平衡力矩阵。CRISFIELD［18］也指出，结构非线性有限元计算的精度主要由不平衡力的计算决定，单元切线刚度矩阵的计算仅决定非线性有限元计算的效率。因此，在按5 个等荷载步进行加载时，在同样的收敛精度要求下，若每一步迭代采用本研究的迭代步骤，则仅需3个迭代步；而若采用文献［15］的迭代步骤，则需要不少于5个迭代步。这也表明了本研究方法在保证计算精度的前提下，能较好地提高算法的计算效率。

3.2 算例2

在本算例中，假设当自由端承受水平荷载P（大小为287 500 kN）时，集中荷载作用的悬臂梁的梁长L为10 m、弹性模量E为3.45×107kN m2，具体如图3所示。梁的高度与厚度均为1 m，泊松比μ取为0，并令α=PL2/EI，P是外荷载，L是梁的长度，E为弹性模量，I为截面抗弯惯性矩。沿悬臂梁的高度方向，将其分别均匀划分成10、20层，沿其长度方向均分成50段。

图3 端部承受集中荷载的悬臂梁（单位：m）Fig. 3 Cantilever beam subjected to concentrated load at free end（unit： m）

在这两种划分方式下，分别形成了561个节点、1 000个单元及1 071个节点、2 000个单元的两种有限元网格。本算例将荷载P分成10 级增量，采取逐渐施加的方式，并采用荷载增量法对其结构非线性方程组进行求解。对于梁端截面1/2 高度处节点A的垂直位移w，本研究计算值和线型方程的解析解［22］进行了对比，结果如图4 所示。在图4 中，计算值1 是将悬臂梁划分为1 000 个单元的网格计算得到的，计算值2则是将悬臂梁划分为2 000个单元的网格计算得到的。

图4 荷载-竖向位移曲线Fig. 4 Load-vertical displacement diagram

从图4 中可以看出，第一种网格划分（1 000 个单元）下的计算精度较差，其中，当α为1 时，解析解和数值解分别为3.017 2 m 和5.375 8 m，相对误差为78.2%。当α为10时，解析解和数值解分别为8.106 1 m和8.328 4 m，相对误差为2.74%；但将该悬梁臂进行更细致地划分，分隔成第二种网格（2 000 个单元）后，计算精度得到了提高。其中，当α为1 时，解析解和数值解分别为3.017 2 m 和3.322 2 m，相对误差为10.10%，当α为10 时，解析解和数值解分别为8.106 1 m 和8.137 3 m，相对误差为0.38%。当α分别为0（初始状态）、1、5及10时，悬臂梁的变形如图5所示。

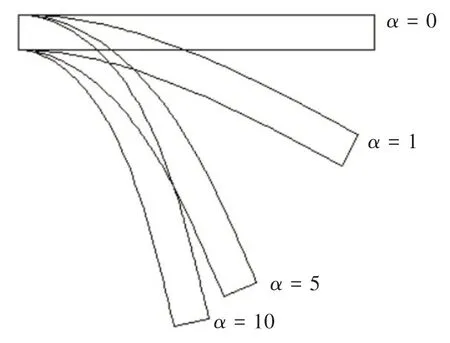
图5 悬臂梁的变形Fig. 5 Deformation configuration of cantilever beam

为了比较本研究的推导算法与ANSYS 商业数值软件算法的优劣，本研究也采用ANSYS 商业数值软件对该算例进行了仿真与计算。其单元网格划分与本研究的第二种网格划分（2 000 个单元）完全相同，也取10个荷载步进行计算。为便于与本研究所导出的单元进行比较，采用由 Plane 42 单元退化的三角形单元。当α为10时，由ANSYS商业数值软件计算得到的悬臂梁变形及初始状态如图6所示。

图6 悬臂梁的变形Fig. 6 Deformation configuration of cantilever beam

从图6 可以看出，当α为10 时，ANSYS 商业数值软件计算的节点A的垂直位移w为8.180 8 m，该值与线性方程组解析解的相对误差为0.92%，而本研究算法仅与解析解的相对误差仅为0.39%。因此，本研究算法的精度略高于ANSYS 商业数值软件的计算精度。

4 结论

1） 通过合理确定共旋坐标系原点及坐标轴方向，结合虚功原理与几何一致性原则，建立基于共旋法的具有对称切线刚度矩阵的几何非线性三角形平面单元，从而避免切线刚度矩阵不对称给非线性方程组求解带来的麻烦。

2） 基于本研究推导公式及算法程序得到的数值解与已有文献数值解及经典解析解均吻合良好。且在同等条件下，本研究对经典算例的计算精度略高于ANSYS 商业数值软件的计算精度。为提高结构非线性分析的精度和效率，可将本研究方法推广至高阶单元，如六节点的三角形单元。

3） 利用共旋法特有的几何非线性与材料非线性解耦的特点和优点，可将本研究方法拓展到钢筋混凝土结构的几何与材料的双非线性分析研究中，这也是下一阶段工作将重点研究的内容。