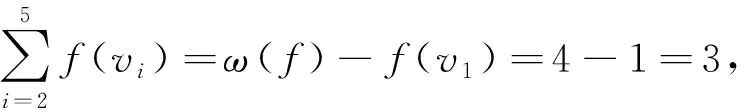图的全局意大利控制数
郝国亮,吴愉琪,曾淑婷
(1.东华理工大学理学院,江西 南昌 330013;2.菏泽学院数学与统计学院,山东 菏泽 274015)
1 预备知识
近几十年来,基于不同的应用背景,图的控制参数问题得到了广泛研究.[1-2]1999年,Stewart[3]提出了君士坦丁大帝时期防御罗马帝国的策略“Defend the Roman Empire”.基于该策略,Cockayne等[4]引入了图的罗马控制的概念.2016年,Chellali等[5]将“Defend the Roman Empire”中的防御策略弱化,提出了图的罗马{2}-控制数的概念.随后,罗马{2}-控制被Henning等[6]重新命名为意大利控制.Gao等[7]计算了笛卡尔乘积图的意大利控制数的精确值.Varghese等[8]研究了边的增加对意大利控制数的影响.Banerjee等[9]给出了计算余图的完美意大利控制数的线性时间算法.本文将研究图的全局意大利控制问题,给出了一般图的全局意大利控制数的界并且得到了某些特殊图的全局意大利控制数的精确值.
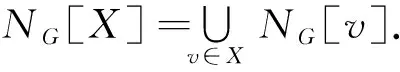


2 主要结论及其证明
命题1 对任意n阶图G,min{n,4}≤γgI(G)≤n.
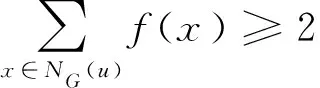



由于0 证明当n∈{3,4}时,由命题1知,γgI(Fn)=n.设n≥5且设扇形图Fn是由路Pn-1=v2v3…vn和一个不在路Pn-1上的顶点v1组成,且使得v1与其他顶点都相邻. 若5≤n≤10,由命题1,要证明γgI(Fn)=4成立,只需要证明γgI(Fn)≤4即可.如果n=5,则定义F5的全局意大利控制函数g使得g(v5)=0,且当i≠5时g(vi)=1,于是γgI(F5)≤ω(g)=4;如果n∈{6,7},则定义Fn的全局意大利控制函数g使得当i∈{1,2,5,6}时g(vi)=1,且当i∉{1,2,5,6}时g(vi)=0,于是γgI(Fn)≤ω(g)=4;如果n∈{8,9},则定义Fn的全局意大利控制函数g使得当i∈{1,2,5,8}时g(vi)=1,且当i∉{1,2,5,8}时g(vi)=0,于是γgI(Fn)≤ω(g)=4;如果n=10,则定义F10的全局意大利控制函数g使得当i∈{1,3,6,9}时g(vi)=1,且当i∉{1,3,6,9}时g(vi)=0,于是γgI(F10)≤ω(g)=4. 若n≥11,定义Fn的全局意大利控制函数g使得g(v1)=g(v2)=2,g(v3)=1且当i∉{1,2,3}时,g(vi)=0,故γgI(Fn)≤5.往证γgI(Fn)≥5.由命题1,只要证明γgI(Fn)≠4即可.反证法.假设γgI(Fn)=4,令f是γgI(Fn)-函数,则ω(f)=γgI(Fn)=4. 断言1f(v1)=1. 这与f是γgI(Fn)-函数矛盾.因此f(v1)=1.断言1得证. 断言2f(vi-1)+f(vi)+f(vi+1)≥1,其中3≤i≤n-1. 事实上,若结论不真,则存在3≤i≤n-1使得f(vi-1)=f(vi)=f(vi+1)=0.则由断言1知, 这与f是γgI(Fn)-函数矛盾.断言2得证. 因为n≥11,所以由断言1和断言2可得 易见上式中“=”成立.因此f(v2)=f(vn)=0.又因为f(v1)=1,所以由γgI(Fn)-函数的定义知,f(v3)≥1且f(vn-1)≥1.因此由断言1和2知, 矛盾.于是当n≥11时,γgI(Fn)≠4. 证明当n∈{3,4}时,由命题1知,γgI(Wn)=n.下设n≥5且设轮图Wn是由圈Cn-1=v2v3…vnv2和一个不在圈上的顶点v1组成,且使得v1与其他顶点都相邻. 假设n∈{6,8,10}.由命题1,要证明γgI(Wn)=4成立,只需证明γgI(Wn)≤4即可.如果n=6,则定义W6的全局意大利控制函数g使得当i∈{2,3}时g(vi)=0,且当i∉{2,3}时g(vi)=1,于是γgI(W6)≤ω(g)=4;如果n∈{8,10},则定义Wn的全局意大利控制函数g使得当i∈{1,2,5,8}时g(vi)=1,且当i∉{1,2,5,8}时g(vi)=0,于是γgI(Wn)≤ω(g)=4. 假设n∈{5,7,9}或n≥11.定义W5的全局意大利控制函数g使得对任意i∈{1,2,3,4,5},g(vi)=1,于是γgI(W5)≤ω(g)=5.当n∈{7,9}或n≥11时,定义Wn的全局意大利控制函数g使得g(v1)=2,当i∈{2,3,4} 时g(vi)=1,且当i∉{1,2,3,4} 时g(vi)=0,于是γgI(Wn)≤ω(g)=5.接下来证明:当n∈{5,7,9}或n≥11时,γgI(Wn)≥5.由命题1,只需要证明γgI(Wn)≠4.用反证法.假设γgI(Wn)=4,令f是γgI(Wn)-函数,则ω(f)=γgI(Wn)=4. 断言1f(v1)=1且对任意i∈{2,3,…,n},f(vi)∈{0,1}. 事实上,类似于定理2中断言1 的证明可得f(v1)=1.往证对任意i∈{2,3,…,n},f(vi)∈{0,1}.用反证法.不失一般性,若f(v2)∉{0,1},则显然f(v2)=2.于是 因此f(v3)和f(vn)中至少一个为0,不妨假设f(v3)=0,于是 这与f是γgI(Wn)-函数矛盾.因此对任意i∈{2,3,…,n},f(vi)∈{0,1}.断言1得证. 类似于定理2 中断言2 的证明可得如下断言: 断言2f(vi)+f(vj)+f(vk)≥1,其中2≤i,j,k≤n且NWn(vj)-{v1}={vi,vk}. 断言3 不存在3个顶点vi,vj和vk使得f(vi)=f(vk)=1且f(vj)=0,其中2≤i,j,k≤n且NWn(vj)-{v1}={vi,vk}. 事实上,若结论不真,不失一般性,假设f(v2)=f(v4)=1且f(v3)=0.又因为f(v1)=1,所以 这与f是γgI(Wn)-函数矛盾.于是断言3得证. 与假设γgI(Wn)=4矛盾. 综上所述,对任意n∈{5,7,9}或n≥11,γgI(Wn)≠4.