半Markov跳变系统的有限时间耗散控制
李秀英,姜 囡
(1.通化师范学院数学学院,吉林 通化 134002;2.中国刑事警察学院声像资料检验技术系,辽宁 沈阳 110854)
0 引言
众所周知,Markov跳变系统作为一类特殊的混杂系统在电力系统、经济系统和网络控制系统等方面具有广泛应用[1-6].但在Markov跳变系统中,Markov过程的驻留时间遵循指数分布,从而系统的转移概率是常数.而半Markov跳变系统的驻留时间可以延伸到更普遍的分布,对比Markov跳变系统,半Markov跳变系统在实际问题中占有更重要的地位.文献[7]研究了半Markov跳变系统的输出反馈滑膜控制;文献[8]给出了一类驻留时间依赖转移概率的半Markov跳变系统的模态依赖H∞滤波器设计方法;文献[9]考虑了具有时变时滞的半Markov跳变系统的输出反馈控制问题;文献[10]研究了一类具有时滞的半Markov跳变神经网络系统的基于滤波器的故障检测问题.
有限时间稳定是指系统的状态在有限时间内不超过某个设定的阈值,因此,有限时间稳定能更好地刻画系统的瞬态性能.文献[11]针对有限频段Markov跳变系统,研究了有限时间H∞滤波问题;文献[12]研究了半Markov跳变系统的有限时间的H∞控制问题;文献[13]研究了具有一般转移概率的半Markov跳变系统的有限时间随机稳定性分析与控制问题.
耗散控制是H∞控制的推广,在系统稳定性理论研究中具有举足轻重的作用,但关于半Markov跳变系统的有限时间耗散控制的研究成果还不多见.本文针对一类半Markov跳变系统,考虑了该系统的有限时间耗散性分析与控制器设计问题.将严格耗散概念引入半Markov跳变系统,设计了模态依赖耗散状态反馈控制器,使闭环系统有限时间有界且严格耗散,给出了数值算例表明所给方法的有效性.
本文对于实对称矩阵X,Y,X 考虑如下连续半Markov跳变系统: (1) 其中:x(t)∈n是状态向量;u(t)∈m是控制输入;ω(t)∈p是外部输入且取值于L2[0,+∞)空间;z(t)∈q是控制输出;x0,r0,t0分别表示初始状态、初始模态与初始时间;{r(t),t≥0}是取值在有限集合S={1,2,…,N}内的连续时间半Markov过程,为表述方便,对任意的r(t)=i∈S,记r(t)的函数f(r(t))=f(i).对任意的r(t)=i∈S,Ai,Bi,Ci,Di,Gi,Hi是已知的适当维数的矩阵. 半Markov过程{r(t),t≥0}中,从模态i到模态j的转移概率为 (2) 其中: (3) 注1 半Markov过程中的转移概率λij(h)是依赖于驻留时间h的时变的函数,较Markov过程具有更广泛的研究意义. 假设1 对于给定的正数τ与T,外部输入ω(t)是时变的且满足以下约束条件: 针对系统(1),当u(t)=0时,给出如下定义: 定义1[12]称系统(1)是关于(c1,c2,T,Mi,τ)有限时间有界的,如果满足 其中0 注2 当系统(1)中ω(t)=0时,有限时间有界转化为有限时间稳定,这表明有限时间稳定是有限时间有界的特殊情形. 考虑系统(1),当u(t)=0时,引入二次型能量函数 G(ω,z,T)=〈z,Qiz〉T+2〈z,Siω〉T+〈ω,Riω〉T, 定义2 给定对称矩阵Qi,Ri和矩阵Si,称系统(1)的自治系统(u(t)=0)是严格(Qi,Si,Ri)-耗散的,如果存在α>0,使得在零初始条件下,对任意的实数T≥0,有 E{G(ω,z,T)}≥αE{〈ω,ω〉T}. 假设2Qi≤0. 本文目的是对系统(1),设计模态依赖状态反馈控制器 u(t)=K(r(t))x(t), (4) 使闭环系统 (5) 是有限时间有界且严格(Qi,Si,Ri)-耗散的,相应的控制器称为有限时间耗散状态反馈控制器. 引理1[12]设τ1与τ2是有界的驻留时间且满足0≤τ1≤τ2.若对于任意t∈[τ1,τ2],V(x(t),r(t),t)与LV(x(t),r(t),t)是有界的,则 注3 本文假设满足引理1的条件. 引理2[12]设W∈n×n是对称矩阵,x∈n是任意向量,则以下不等式成立: λmin(W)xTx≤xTWx≤λmax(W)xTx. 定理1 令u(t)=0,给定常数c1>0,T>0及对称矩阵Qi,Ri和矩阵Si,半Markov跳变系统(1)是关于(c1,c2,T,Mi,τ)有限时间有界的.若在假设1下,则存在常数α>0,ρ>0和矩阵Pi>0,i∈S使得 (6) (7) (8) 其中 证明对系统(1)(u(t)=0),选取Lyapunov函数V(x(t),r(t),t)=xT(t)P(r(t))x(t),令L表示半Markov过程{r(t),t≥0}的弱无穷小算子,有 由(6)式可得LV(x(t),r(t),t)≤αV(x(t),r(t),t)+ρ2ωT(t)ω(t). 以e-αt乘上式两边得E{L[e-αtV(x(t),r(t),t)]}≤ρ2e-αtωT(t)ω(t),由引理1有 由引理2有 于是利用假设1有 (9) 同时 (10) 由(9)与(10)式可得 因此,由定义1知系统(1)关于(c1,c2,T,Mi,τ)有限时间有界. 定理2 令u(t)=0,给定常数c1>0,T>0及对称矩阵Qi,Ri和矩阵Si,半Markov跳变系统(1)是关于(c1,c2,T,Mi,τ)有限时间有界且严格(Qi,Si,Ri)-耗散的.若在假设1与假设2下,则存在常数α>0,ρ>0和矩阵Pi>0,i∈S使得 (11) (12) 证明利用Schur补引理,由(11)和(12)式可得 (13) 由定理1知系统(1)关于(c1,c2,T,Mi,τ)有限时间有界.令 J(t)=-zT(t)Qiz(t)-2zT(t)Siω(t)-ωT(t)Riω(t), 当(13)式成立时有 LV(x(t),r(t),t)≤αV(x(t),r(t),t)-J(t), 则 E{L[e-αtV(x(t),r(t),t)]}≤-E{e-αtJ(t)}. 在零初始条件下有 于是 E{G(ω,z,T)}≥αE{〈ω,ω〉T}, 即系统(1)是严格(Qi,Si,Ri)-耗散的,于是定理2成立. 注4 当Qi=-I,Si=0,Ri=γ2I时,定理1的结果转化为H∞性能,同时说明系统(1)关于(Qi,Si,Ri)-的严格耗散性包括H∞性能. 定理3 令u(t)=0,给定常数c1>0,T>0及对称矩阵Qi,Ri和矩阵Si,半Markov跳变系统(1)存在有限时间耗散状态反馈控制器.若在假设1与假设2下,则存在常数α>0,ρ>0和矩阵Xi>0,i∈S,Wij>0,i,j∈S,i≠j及矩阵Yi>0,i∈S使得(12)式与以下条件成立: (14) (15) (16) 其中: 证明将(11)式中的Ai,Ci分别替换为Ai+BiKi,Ci+DiKi,有 (17) (18) 考虑形如系统(1)的半Markov跳变系统,系统参数如下: 模态1为 模态2为 对于i=1,2,设半Markov过程{r(t),t≥0}服从韦布尔分布,即 f1(h)=f2(h)=2he-h2,h>0, 则转移概率矩阵为 转移概率λ12(h)的数学期望为 取α=1,ρ=1,根据定理3可得 本文针对半Markov跳变系统,通过线性矩阵不等式和构造Lyapunov函数的方法,给出了半Markov跳变系统的有限时间耗散状态反馈控制器的存在条件和设计方法,该控制器能保证闭环系统有限时间有界且严格耗散.数值算例结果表明,控制器可通过求解线性矩阵不等式而得到.1 预备知识


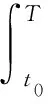

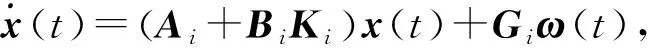
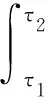
2 有限时间耗散性分析

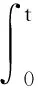

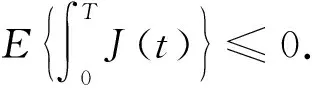
3 有限时间耗散控制
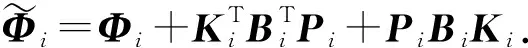

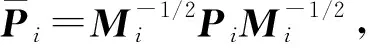
4 数值算例
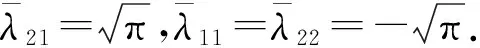
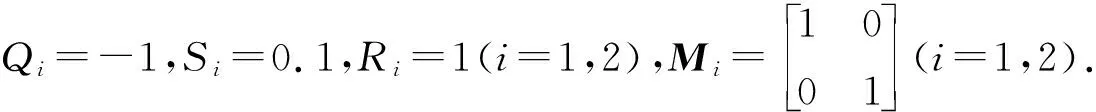
5 结 论

