电磁效应下耦合时滞神经元动力学分析
何沛妍,杨丽新,党元辰,顾梓玉
(陕西科技大学数学与数据科学学院,陕西 西安 710021)
0 引言
对于自然界中生命体的生存和活动来说,神经系统是重要的信息中心,神经元作为神经系统的基本组成单元,对神经信息的传导和控制至关重要[1-2],不同的外界刺激条件对神经元的放电节律会产生不同的影响[3],神经元之间的信息传递也会产生丰富的动力学行为[4-5].若神经系统没有受到任何扰动与输入信号的作用,则对应的输出量会保持在某一状态上;神经系统也可以在相应的控制中将神经元活动输出为特定行为,Rinzel等[6]发现这些行为的差异是由于兴奋性的分岔机制不同,其产生的分岔类型决定了神经元的计算特性[7],因此,神经系统的稳定性和分岔问题备受关注.
在对神经元深入学习的过程中,神经元数学模型的丰富与完善对神经系统的研究有推进意义.1961年,Fitzhugh和Nagumo等[8-9]对Hodgkin-Huxley(HH)模型[10]进行简化,提出FHN模型,它可以模拟多种神经元行为[11].Bashkirtseva等[12]用随机灵敏度函数法分析了FHN模型的兴奋性,发现噪声引起的模型动力学变化可以用其吸引子的高随机敏感性来解释.大多数情况下,神经元处于的环境复杂,离子在细胞膜内外运动与传输时,会导致细胞内外电磁场分布改变,产生电磁效应,大多数研究采用磁通量来刻画.Ge等[13]研究了FHN神经元系统在电磁感应作用下高频刺激驱动的弱低频信号所产生的振动共振现象、集体行为等.文献[14]研究了ML神经元模型在磁场的作用下簇放电的类型及分岔过程,讨论了适当的耦合连接对神经元之间放电模式转迁的作用.然而,在生物和人工神经系统中,时间延迟是普遍存在的,会使系统产生更加复杂的动力学行为[15].文献[16]提出了一种带有时滞的FHN耦合神经系统,发现信号传输的时间延迟对于FHN神经系统中同步尖峰的发生至关重要.文献[17]考虑了神经元内外电磁场分布所产生的电磁效应,并讨论了神经元系统所产生的动力学行为,揭示了电磁刺激对神经元系统的动力学行为有调控作用,但其没有考虑到时间延迟在系统中的影响.
基于上述研究,本文同时考虑电磁效应和时滞,建立新的耦合FHN模型,借助时域法研究电磁效应下系统所产生的动力学行为,利用Routh-Hurwitz判据来判断系统的稳定性,利用中心流形定理和规范型理论来分析系统所产生周期解的稳定性,并进行数值模拟,讨论在不同条件下,施加电流刺激对系统稳定性的影响.
1 模型描述
1961年,Fitzhugh等建立了FHN神经元模型,可以表示为[18]
(1)
其中:x,y分别表示FHN神经元的膜电位和恢复变量;ε,a和b均表示为常数.
近年来,许多研究者对FHN神经元模型动力学行为进行了探索.其中,文献[19]仅仅对单个神经元的动力学行为进行了讨论,而耦合是神经元之间的连接桥梁,可以实现信号和能量的传递.文献[20]分析的对象是两个神经元耦合的神经系统,但其忽略了电磁效应的影响.因此,本文考虑神经元中电磁场分布改变产生的电磁效应以及神经元在传递和处理信息过程中产生的时间延迟,将两个FHN神经元耦合,并且引入两个时滞,建立了电磁效应下带有时滞的耦合FHN模型:
(2)
其中:x1,x2表示两个神经元的膜电位;y1,y2表示两个神经元的恢复变量;φ表示在电磁效应下通过两个神经元之间的磁通量;ρ(φ)表示忆阻器的记忆电导[21],并且ρ(φ)=α+3βφ2,α表示恒定的电导,β表示磁通反馈率;k1,k2,k3表示反馈增益;Iext1,Iext2表示神经元上的外部刺激电流;τ1,τ2表示时滞.
2 平衡点的稳定性分析
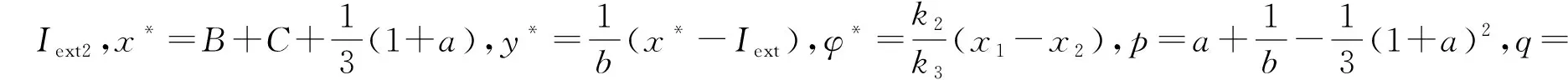
对系统(2)作变换:u1=x1-x*,v1=y1-y*,u2=x2-x*,v2=y2-y*,w=φ-φ*,则可得其线性化部分为
(3)
其中:A=(1+a)2x*-3(x*)2-a-k1ρ(φ),B=-1,E=k1ρ(φ),G=ε,H=-εb,J=k2,K=-k2,L=-k3.
并将系统(3)改写为向量的形式为
(4)
其中u=(u1,v1,u2,v2,w)′,
若u=me-λt(m≠0)是系统(4)的解,则m(λI-A1-A2e-λτ1-A3e-λτ2)=0,其特征方程为
λ5+P1λ4+P2λ3+P3λ2+P4λ+P5+(P6λ2+P7λ+P8)e-λ(τ1+τ2)=0,
(5)
其中:P1=-2(A+H)-L,P2=2AH-2BG+(A+H)2+2L(A+H),P3=2(A+H)(-AH+BG)-(2AH-2BG)L-L(A+H)2,P4=A2H2+B2G2+(A+H)(2AHL-2BGL),P5=-A2H2L-B2G2L,P6=-GE2,P7=GHE2+GE2L,P8=-GHE2L.
在平衡点Q*(x*,y*,x*,y*,φ*)处,时滞τ1,τ2对系统(1)稳定性的影响分为τ1=τ2=0和τ1+τ2=τ>0两种情况来讨论[22].
当τ1=τ2=0时,特征方程变为
λ5+O1λ4+O2λ3+O3λ2+O4λ+O5=0,
(6)
其中:O1=P1,O2=P2,O3=P3+P6,O4=P4+P7,O5=P5+P8.由Routh-Hurwitz判据[23]可以得到:若Hi>0(i=1,2,3,4,5),特征值λ的实部均为负数,则系统(3)是局部渐进稳定的.其中Hi为特征方程的系数所构成的矩阵.
当τ1+τ2=τ>0时,特征方程变为
λ5+P1λ4+P2λ3+P3λ2+P4λ+P5+(P6λ2+P7λ+P8)e-λτ=0.
(7)
假设方程(7)有纯虚根λ=wi(w>0),则
w5i+P1w4-P2w3i-P3w2+P4wi+P5+(-P6w2+P7wi+P8w)e-wτi=0.
(8)
分离方程(8)的实部和虚部为
(9)
其中ai(i=1,2,3,4,5,6)是关于w的多项式,a1=P1w4-P3w2+P5,a2=-P7w,a3=-(P6w2-P8),a4=w5-P2w3+P4w,a5=P6w2-P8,a6=-P7w.
由方程组(9)可以得到
(a2a4-a1a5)2+(a1a6-a3a4)2-(a2a6-a3a5)2=0.
(10)
若方程(9)中存在一个正实根w0,从方程(9)解得
(11)
令λ(τ)=α(τ)+w(τ)i是方程(7)在τ=τ0的一个根,并且满足α(τ0)=0,w(τ0)=w0,可得
(12)
因此,当τ=[0,τ0),系统(1)在平衡点Q*(x*,y*,x*,y*,φ*)处是局部渐近稳定的;当τ=τ0时,系统(1)在平衡点Q*处产生了Hopf分岔;当τ>τ0时,系统(1)在平衡点Q*处不稳定.
3 周期解的稳定性分析
通过对系统(1)在平衡点Q*(x*,y*,x*,y*,φ*)处的稳定性分析,发现在τ0处会存在Hopf分岔,将规范型理论和中心流形定理[25]相结合来讨论周期解的性质.

(13)
令Y(t)=(u1,v1,u2,v2,w)T,系统(13)记为Y′(t)=(τ0+ρ)A1Y(t)+(τ0+ρ)A4Y(t-1).
对于φ=(φ1,φ2,φ3,φ4,φ5)T∈C([-1,0],R5),定义有界线性算子Lρ(φ)和非线性算子f(ρ,φ)分别为
Lρ(φ)=(τ0+ρ)A1φ(0)+(τ0+ρ)A4φ(-1),
(14)
f(ρ,φ)=(τ0+ρ)(f1,f2,f3,f4,f5)T,
(15)
(16)
(14) 式中:
(15)式中:
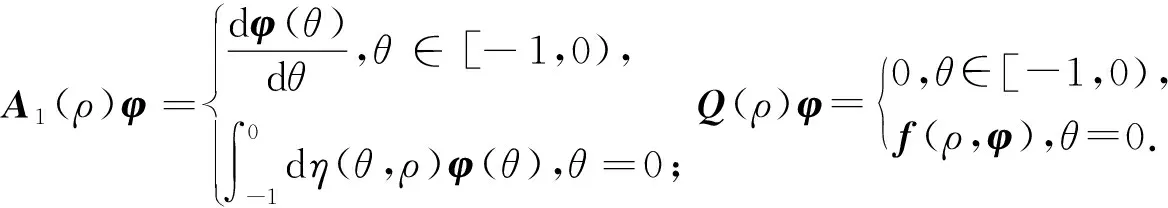
(17)
(18)
对于ψ∈C1([0,1],(R5)*),η(θ)=η(θ,0),定义伴随线性算子A*和双线性内积〈ψ(s),φ(θ)〉为:
(19)
(20)

(21)
(22)
(23)
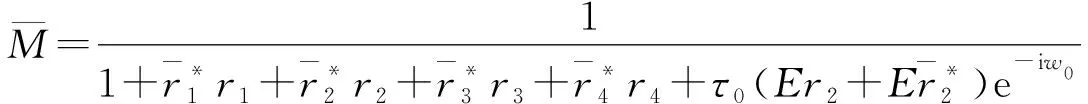
根据中心流形定理,可以得到
(24)
其中:
综上所述,可以得到:
其中:μ2决定Hopf分岔的方向,β2决定分岔周期解的稳定性,T2决定分岔周期解的周期[26].
4 数值模拟
将分岔参数与输入信号相结合来研究时滞和施加电流刺激对系统(1)的影响,取系统的初始状态值为(0.43,0.02,0.03,0.4,0.5),设定系统中各参数的值为a=0.5,b=0.9,ε=1.5,k1=15,α=6.8,β=1,k2=-1.7,k3=1.在所取参数条件下,可得系统(1)的平衡点为(0,0,0,0,0).通过计算可以得到g20=g11=g02=0.019 0+0.007 9i,g21=-0.016 3+0.001 7i,λ′(τ0)=-0.129 2-0.156 9i,则C1(0)=-0.007 5+0.000 2i.由上节对Hopf分岔分析可以得到:μ2=-0.058 0<0,β2=-0.015 0<0,T2=-0.028 6<0,系统会发生亚临界Hopf分岔,存在分岔周期解,并且分岔周期递减.
首先分析未施加电流刺激时带有时滞的耦合神经元系统放电行为.
当τ1=τ2=0时,系统(1)在零平衡点是渐进稳定的,如图1所示,系统中状态变量的时间变化曲线从初始状态有小幅度波动,在t=5时刻趋近于(0,0,0,0,0).
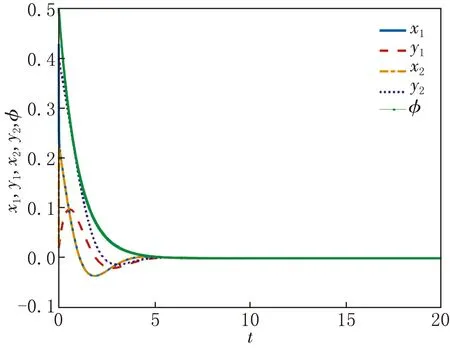
图1 τ=0时系统(1)的时间序列图
当τ1+τ2=τ>0时,由方程(12)可得w的一个正实值w0=0.382 4,可以得到系统的一组临界时滞为τj=0.850 4,17.281 4,…(j=0,1,2,…).
当τ=0.450 4<0.850 4时,时滞对系统的影响不大,系统在零平衡点是渐进稳定的,如图2所示.神经元系统的状态变量在时滞的作用下出现振荡,但在一定的时间内会趋近于零平衡点,维持稳定;当τ=0.850 4时,系统在零平衡点附近振荡,失去了稳定性,呈现出周期放电状态,系统是混沌的,如图3所示.从系统(1)的状态变量所对应的相图可以看出,系统存在混沌吸引子.
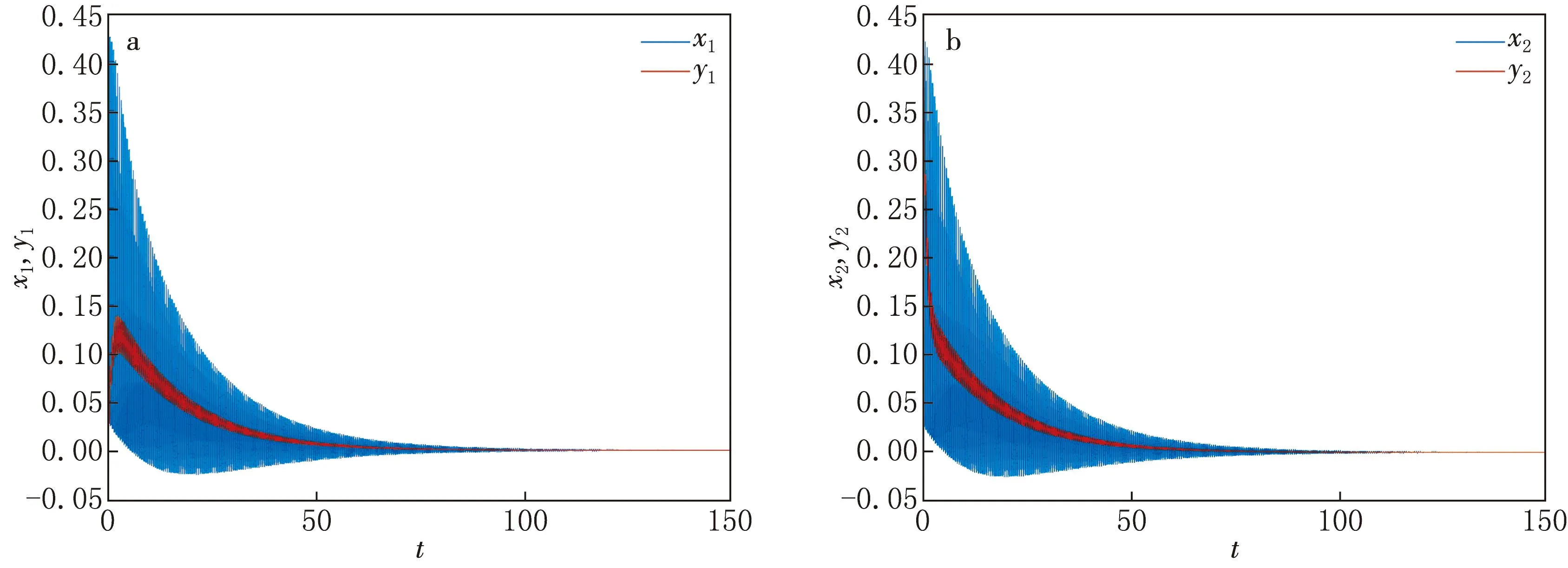
图2 τ=0.450 4时系统(1)的状态变量随时间演化历程图
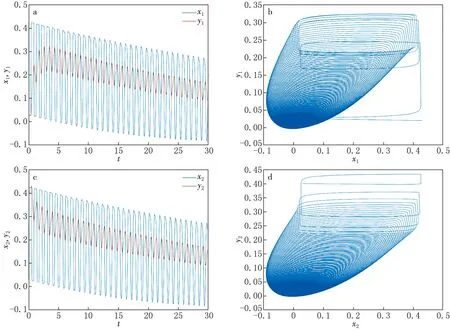
图3 τ=0.850 4时系统(1)的状态变量随时间的演化历程图及平面内的相图
由于带有时滞的耦合FHN神经元系统在临界时滞处发生亚临界Hopf分岔,会导致系统的平衡失去稳定性,因此,施加电流刺激来控制系统的放电行为,研究电流刺激对系统产生的影响,在不同时滞下,改变Iext1,Iext2的值,所施加的刺激电流单位为mA·(cm2)-1.
当τ=0时,施加电流刺激,系统的平衡点会发生改变,而平衡状态不会发生改变,如图4所示.当τ=0.850 4时,若对系统中一个神经元施加电流刺激,如图5(a)和(b)所示,系统的状态变量的振荡区域发生改变,系统放电状态的周期发生变化;若对系统中两个神经元同时施加电流刺激,神经元系统的状态变量在振荡之后会趋于平稳,如图5(c)所示,状态变量的平衡点也发生改变.该神经元系统从周期放电模式转化为静息状态,系统稳定.因此,时滞和电流刺激的变化会对系统的动力学行为产生影响,施加电流刺激可以改变系统的混沌状态.
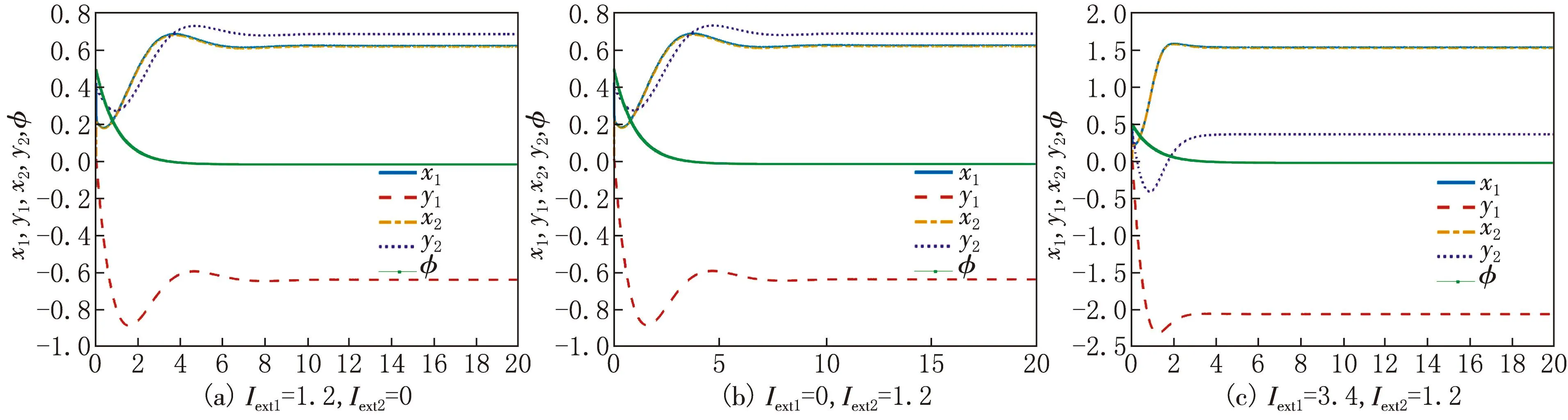
图4 τ=0时施加不同的电流刺激,系统(1)的时间序列图
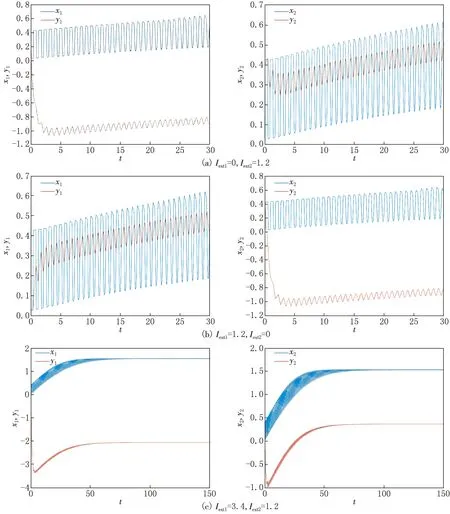
图5 τ=0.850 4时施加不同的电流刺激,系统(1)的状态变量随时间的演化历程图
5 结论
本文基于FHN神经元模型,考虑了神经元之间信息传递所产生的时间延迟和神经元内外电磁场分布变化,建立了在电磁作用下带有时滞的耦合FHN神经元模型.利用时域法研究了Hopf分岔的存在及其性质,分析了时滞与电流刺激对神经元系统的动力学影响.通过对该模型在平衡点处稳定性的讨论,发现τ0=0.850 4是临界时滞,当τ<τ0时,神经元系统在平衡点处渐近稳定;当τ>τ0时,产生了亚临界Hopf分岔,系统失稳,在平衡点附近发生振荡.当对其中一个带有时滞的神经元施加一定的电流刺激时,该神经元的振荡幅度减小;当对该模型中的两个神经元同时施加电流刺激时,该模型从周期放电模式跃迁为静息状态,从振荡状态转变为渐近稳定,并且平衡点位置发生改变.从上述结论可以得到,时滞对神经元系统的动力学行为有一定的影响,施加相应的电流刺激会调控系统的机制,维持系统的稳定状态,这对利用合理的外部刺激方式来治疗某些精神疾病提供了理论指导.

