关于丢番图方程x(x+1)(x+2)(x+3)=68y(y+1)(y+2)(y+3)

林丽娟

(重庆化工职业学院 通识教育学院,重庆 401228)

引言

数论是研究整数性质的一个数学分支,丢番图方程是数论中的一个十分重要的课题。对于丢番图方程Mx(x+1)(x+2)(x+3)=Nyy(y+1)(y+2)(y+3),n∈N+,当M=1时已有不少研究工作。1971年Cohn[1]证明了N=2时仅有正整数解(x,y)=(5,4),1975年Ponnudurai[2]找到了N=3时的解的情况,1982年宣体佐[3]给出了N=5时的解的情况,1991年和2001年罗明[4,5]分别给出了N=7,6时的解的情况。总体上看,对于N<100时的正整数解的研究得到了一些结果[6-12],但由于丢番图方程求解的困难性,仍然还有一些情况没有解决。本文利用Pell方程基本解性质、递推序列、同余思想以及二次剩余,研究不定方程

x(x+1)(x+2)(x+3)=68y(y+1)(y+2)(y+3)

(1)

N=68时的情况,证明了该方程仅有2组非平凡整数解。

1 预备知识

先将方程(1)化为

(x2+3x+1)2-68(y2+3y+1)2=-67

(2)

易知方程X2-68Y2=-67的全部整数解由以下两个结合类给出[13]:

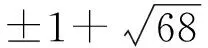
(2y+3)2=±4yn+5,n∈Z

(3)

容易验证下列关系式成立:

un+1=66un-un-1,u0=1,u1=33

(4)

vn+1=66vn-vn-1,v0=0,v1=4

(5)

yn+1=66yn-yn-1,y0=1,y1=37

(6)

u2n=2un2-1,v2n=2unvn

(7)

yn=un+vn

(8)

un+2kh≡(-1)k(moduh),vn+2kh≡(-1)kvn(moduh)

(9)

yn+2kh≡(-1)kyn(moduh)

(10)

2 定理证明

2.1 当(2y+3)2=-4yn+5时

引理1-4yn+5是平方数仅对n=0成立。

证明 当n≠0时,yn>1,故-4yn+5<0,即(2y+3)2<0,不可能是一个平方数;当n=0时,-4yn+5=1是平方数。

2.2 当(2y+3)2=4yn+5时

引理2若4yn+5是平方数,则必须n≡0,-1(mod23×3×5)。

证明 采用对序列{4yn+5}取模的方法分三步来证明,先证明n≡0,-1(mod5),再证明n≡0,-1(mod3),最后证明n≡0,-1(mod8)。

步骤1 先取mod4421,可得n≡0,1,4(mod5),取mod4289,可排除n≡1,6(mod10)即排除n≡1(mod5),故得n≡0,-1(mod5)。

步骤2 要证n≡0,-1(mod3),只需排除n≡1(mod3),等价于排除n≡1,4,7,10,13,16,19,22(mod24)。取mod824231,可排除n≡1,7,13,16,19(mod24),再取mod1451,可排除n≡10,22(mod24),剩下n≡4(mod24)等价于n≡4,28(mod48),再取mod79即可排除。故得n≡0,-1(mod3)。

步骤3 取mod11,可得n≡0,2,3(mod4)等价于n≡0,2,3,4,6,7(mod8)。再取mod7,可排除n≡6(mod8),可以得n≡0,2,3,4,7(mod8),再依次取mod79,119983,可排除n≡2,3,4,10,11,12(mod16),得n≡0,7,8,15(mod16),等价于n≡0,-1(mod8)。

综上所述,n≡0,-1(mod8×3×5)。

引理3设4|n,n>0,则

引理4设n≡0(mad23×5),则仅当n=0时,4yn+5是平方数。

证明 当n=0时,4yn+5=32是一个平方数。若n≡(mod23×5)且n≠0时,则可令n=0+2×5×k×2t,t≥2,k为奇数,若取m为2t,5×2t之一,则由(8)、(9)、(10)得

4yn+5≡4un+4vn+5n≡±4v2m+5(modu2m)

{5um±4vm}对mod143的剩余序列周期为12,而{2t}对mod12的剩余序列周期为2。

引理4得证。

引理5设n≡-1(mod8×3×5)则仅当n=-1时,4yn+5是平方数。

证明 当n=-1时,4yn+5=112是一个平方数。若n≡-1(mod8×3×5)且n≠-1时,则可令n=-1+2×k×3×5×2t,t≥2,k≡1(mod2),取m为2t,3×2t,5×2t,3×5×2t之一,则由(10)可得

4yn+5≡-4y-1+5≡-111(modum)

因为um≡1(mod8),um≡1(mod3)所以

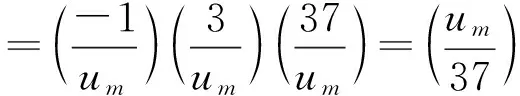
{um}对mod37的剩余序列周期为38,而{2t}对mod38的剩余序列周期为18。

令

则有表1:

表1 t,m,um对应表

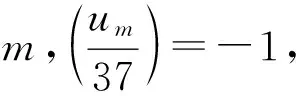
定理证明:

证明由引理1得(2y+3)2=1,即y=-1,-2;由引理4得(2y+3)2=32,即y=0,-3;由引理5得(2y+3)2=112,即y=4,-7;将y代入方程(1)可得全部18组整数解,其中包括16组平凡解使得(1)式两端都为0,有2组非平凡解,即(x,y)=(14,4),(14,-7)。